等离子体环境下高超声速飞行器的流-固耦合机制
2023-11-27王琛田振国沈振兴
王琛, 田振国, 沈振兴
(燕山大学 河北省重型装备与大型结构力学可靠性重点实验室, 河北 秦皇岛 066004)
0 引言
飞行器做再入运动时,将以7~8 km/s的速度穿越地球大气层[1],飞行器前部将形成弓形激波。激波内的气体被强烈压缩,气体压力作功导致气体内能提升,在高能量环境下气体发生热电离、形成高温等离子体气流,飞行器头部承受高温等离子体气流的剧烈作用。除流体荷载与高温作用外,飞行器头部防护罩在高温下也与等离子体发生反应[2],该防护罩承受了热作用、荷载作用和化学作用,并在这三者的耦合作用下发生损毁。此外,在高速气流中,等离子体化学反应物存在尚未反应即被输运出流场的现象,称为化学非平衡。上述现象表明考虑化学非平衡-流体-固体-热耦合后,等离子体流体对于飞行器的流体与固体(简称流固)耦合作用相较于热完全气体将发生改变。
为了考虑这种作用并正确设计防护罩,研究人员采用了多种方法研究飞行器的等离子体流场分布。欧洲航天局的实验数据证明了飞行器以高速在大气层中飞行时[3]激波处能量被激发,此时应采用真实气体描述热力学规律。乐嘉陵等[1]对前人的经典理论做了整理,给出了再入化学反应绕流的基本方程组,其总结的多温度热化学不平衡模型成为近年来高超声速等离子体流场研究所使用的基本理论。韦毅[4]基于单温度和双温度热化学不平衡方程组研究了再入飞行器的等离子体鞘套,计算了等离子体流场、热场、物质场与电子数分布,分析了热化学非平衡对于物种分布和电子数的影响,计算结果表明在球头区域热化学不平衡效应明显。华彩成[5]基于钝锥实验模型进行了数值模拟,并分析了化学反应模型对等离子体流场的影响,发现不同的化学反应模型对流场影响不大,是否考虑热化学非平衡对流场影响较大。常用的化学反应主要由Park[6]、Dunn等[7]和Gupta等[8]给出,由于等离子体反应复杂,当前对于化学反应模型的选取没有形成统一的标准。流固耦合作用计算对于高超声速飞行器设计尤为重要,尽管模拟方法取得了重要进展,但考虑真实气体效应的多物理场耦合问题仍然是一个挑战[9-12]。Schäfer[13]在高焓条件下进行了飞行器流固耦合实验,研究了通用碳化硅复合材料的热变形,并与流固耦合仿真结果[13-15]进行了对比,计算了超声速流固耦合问题,但在速度上仍然较低。在计算方法上,聂涛等[16]也对高超声速飞行器前缘进行了流固耦合计算,并与圆管绕流实验作对比,采用紧耦合的方法同时利用有限元法与有限体积法进行计算,目前该方法是飞行器流固耦合计算的常用办法。紧耦合相对于松耦合[17]计算数值上更加精确,减小了异步迭代误差。李佳伟[18]基于热完全气体研究了高超声速流-固-热多场耦合数值模拟的方法,认为气体物性参数会导致气动力的改变。秦启豪[19]建立了基于计算流体力学(CFD)/计算结构力学(CSD)的多物理场求解策略,计算了热完全气体环境下进气道的流固耦合作用,研究了流场在进气道变形下的振荡。Dennis等[20]进行了高超声速流固耦合问题的薄板风洞实验,拓展了该领域流固耦合问题非常有限的实验数据。Quan等[21]采用CFD方法研究了高超声速热完全气体环境下板构件的气动热弹性特性,认为热荷载与气动荷载的组合可能会对飞行器结构产生不利的作用。
截至目前,尚无一种可以综合考虑等离子体真实气体效应与流固耦合计算的办法,相关研究表明真实气体效应[9-12]与化学非平衡效应[4-5]对飞行器流固耦合影响较大。
本文从考虑等离子体真实气体效应的角度,建立等离子体流固耦合方程组,在经典流固耦合方程和瞬态固体力学平衡方程的基础上,增加再入流场热化学非平衡绕流方程组作为真实气体方程;基于建立的模型计算等离子体对于再入飞行器的流固耦合效应,发现在较高的飞行速度下最大黏性力位置发生迁移,并给出了等离子体热化学流固耦合的计算结果。
1 考虑等离子体的流固耦合模型
考虑到多物理场问题的非线性和复杂性,为利于问题的建模和求解,采用文献[4]的假设。采用Gupta等[8]所提出的等离子体化学反应模型,如表1所示。表1中第三碰撞体为催化反应进行的物质,催化模型见文献[1]。
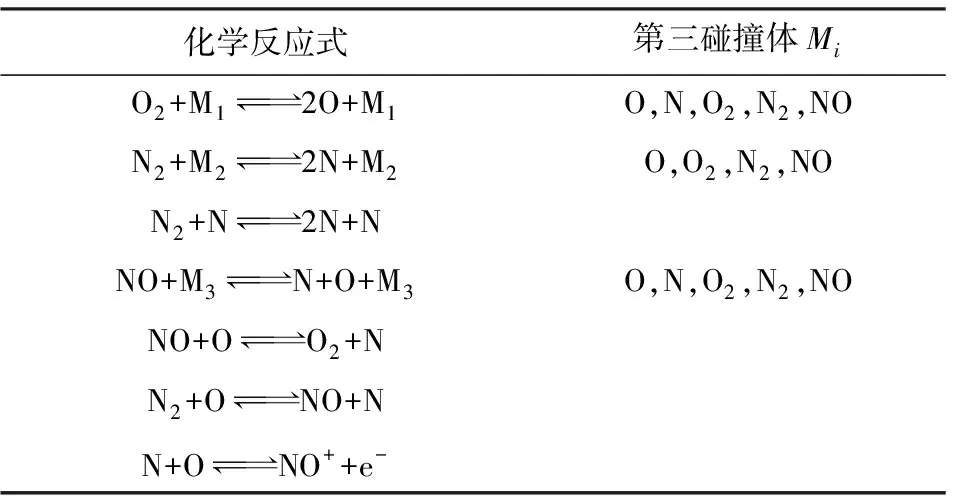
表1 化学反应式Table 1 Chemical reaction
由于飞行速度最高计算至马赫数22,采用7组分18反应模型,若要计算至更高马赫数,则必须考虑更多物种,本文采用的反应参与物种为N2、O2、N、O、NO、NO+和e-。除了化学反应的描述外,还需要各个组分的热力学描述,采用文献[4]给出的热力学表达式。对于第i个物质,基于质量守恒定律建立物质输运方程[1]:
(1)
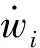
流体黏度和热传导系数按照文献[4]整理的计算方法得到。文献[1]总结了等离子体混合物的性质。根据参考文献[22],采用二维黏性可压缩流体动力学方程组描述混合气体质量输运、动量输运以及能量输运。为便于分析热源,采用热力学温度T描述能量方程:
(2)
式中:p为混合物压力;I为单位矩阵;K为黏性张量;dφ为二维分析的周向厚度,dφ=1;Cp为恒压热容;q为热传导通量;Q为流体热源。在模型中,流体热源来源于等离子体黏性加热,压缩加热和化学产热,基于参考文献[4],为便于计算,将文献中的方程修改为统一的热源项,为
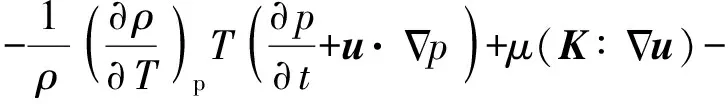
(3)
式中:Qp为压缩加热源项;Qvd为黏性加热源项;Qplasma为化学产热源项;T为温度;μ为混合物流体黏度;hi为物种i的质量焓;Di为物种i的扩散系数;ns为物种数;r为半径。飞行器流固耦合边界承受高超声速飞行的流体荷载,流固耦合边界上的荷载为流体压力和黏性力之和[23],即
Fsum=[-pI+K]·n
(4)
式中:Fsum为流固耦合边界气动荷载;n为流固耦合边界法向量。
建立固体力学瞬态平衡方程[24]为
(5)
式中:S为应力张量;F为体积力;us为固体位移场。在计算中,考虑流体对飞行器的作用,但不考虑飞行器的变形对流体的扰动。
2 考虑等离子体的流固耦合算例
采用美国国家航空航天局(NASA)的RAM-C Ⅱ再入实验飞行器为计算模型,如图1所示。在流体动力学方程和固体力学方程之间建立耦合关系,同时将等离子体化学反应作为能量源项和物质源项参与计算,应用COMSOL软件进行全耦合求解。
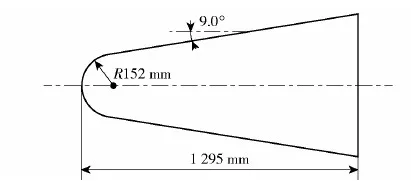
图1 RAM C-Ⅱ的几何尺寸Fig.1 Geometric dimensions of RAM C-Ⅱ
采用基于有限元法的瞬态求解方式,根据参考文献[4]提供的61 km高空条件,有初始条件:
u=[0 m/s,0 m/s],p=27 Pa,T=254 K
(6)
入口边界条件为马赫数入口(马赫数为Ma∞),来流马赫数的大小随着时间的增长而线性增大,出口边界条件为压力出口(pout为出口压力),来流温度T∞和来流压力p∞与初始条件相同。
(7)
考虑飞行器壁面为无滑壁,则壁面速度uw为
uw=[0 m/s,0 m/s]
(8)
考虑来流空气质量分数比例中N2占比0.767,O2占比0.233,其余组分为0。为验证真实气体模型的正确性,将等离子体流场计算结果与文献[4]中的算例作对比。此外,对计算采用的映射网格进行逐次加密,检验数值计算的网格无关性,如表2所示,其中应力为马赫数Ma=22下等离子体环境中固体的最大应力。
由表2可知,不同网格划分程度得到的结论相差不大,因此采用40×(50+4)网格,即采用指数型加密的方式,边界第1层网格厚度为2.5 μm,飞行器边界网格数量为40,垂直于边界向外扩展网格数量为50。对固体区域采用结构化网格,为捕捉到应力梯度,划分4层,层厚为10 mm,如图2所示。
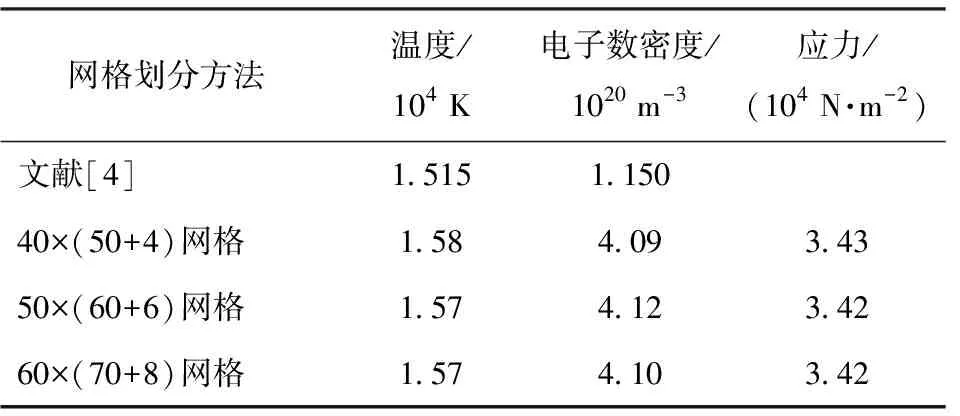
表2 算例检验Table 2 Example test

图2 结构化网格划分Fig.2 Structured meshing
本文算法计算结果与文献[4]的计算结果相差不大,证明了计算模型考虑真实气体效应的可靠性。电子数密度因数值敏感,受算法影响较大,一般在数量级上没有差异即可认定数值上相差不大[4]。
3 流固耦合机制和计算结果讨论
研究考虑等离子体真实气体效应的流固耦合方程,得到以RAM C-Ⅱ飞行器为算例的计算结果。采用热完全气体模型和单温度等离子体模型计算结果对比,分析等离子体气体和其组分对于流固耦合计算的影响,采用匀加速再入体速度,不考虑飞行器的运动姿态,计算出等离子体流场、压力场、温度场和物质场后,对等离子体关于流固耦合的作用机制进行了分析。
3.1 等离子体流固耦合气动冲击和气动摩擦分析
高层大气中,空气的压力性质和黏性力性质相对于热完全气体发生较大变化,二者是改变飞行器气动荷载环境的关键因素。有边界气动压力Fn和边界气动黏性力Fτ分别为
Fn=(Fsum·n)n
(9)
Fτ=Fsum-Fn
(10)
式中:Fsum为飞行器所受的气动合力。
图3的计算结果显示,飞行器由静止加速到Ma=22的加速过程中热完全气体和等离子气体两种气体模型对于再入飞行器的气动作用存在差异,其中当速度Ma=22时,热完全气体和等离子气体的流固耦合作用差别显著。
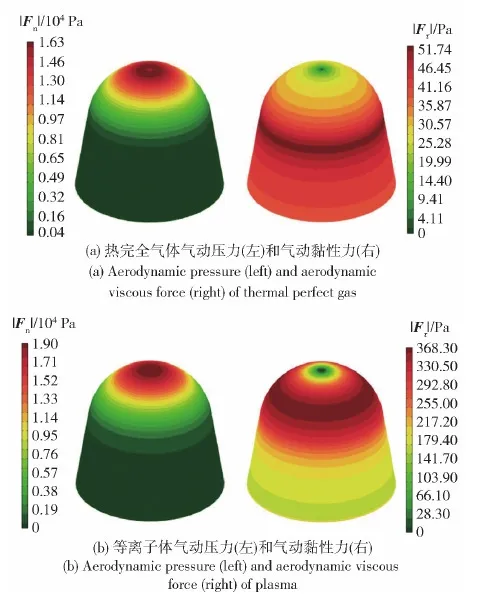
图3 等离子体与热完全气体的气动力对比Fig.3 Comparison of aerodynamic forces between plasma and thermal perfect gas
对比发现,在Ma=22的高速气流作用下,等离子体气动压力由于考虑了真实气体作用,相较于完全气体提升了16.5%,而气动黏性力较完全气体而言提升了611.8%,且最大作用力位置不同,最大黏性力位置和最大压力位置将承受高速高温气体最大的摩擦作用和冲击作用,摩擦位置和冲击位置对于考虑烧蚀作用的再入飞行器设计较为重要,可能是最快磨损烧蚀的位置。由图3可见:在Ma=22的速度下,对于热完全气体,摩擦位置位于中部,冲击位置位于顶部,呈环状;反之,对于等离子气体,摩擦位置位于中上部,冲击位置位于顶部,且覆盖整个飞行器前端,表明了飞行器运动时的实际气体摩擦和冲击状态。以图4(a)所示飞行器边界弧长s为横坐标,以头部为起点,计算不同来流马赫数下的边界气动压力和边界气动黏性力。
由图4(b)、图4(c)、图4(d)可见,由于气动外形相对固定,且来流方向不变,在马赫数为16~22的流速下,最大气动力位置几乎不改变。

图4 等离子体和热完全气体的冲击与摩擦对比Fig.4 Shock and friction comparison for plasma and thermal perfect gas
等离子气体与热完全气体之间的冲击差异主要与等离子体平均粒子动量有关,等离子体采用了精确的组分计算空气的平均摩尔质量。由于等离子气体模型中,计算了各个组分黏性的不同,图4(e)、图4(f)、图4(g)中等离子体气体与热完全气体的摩擦位置相差很大,热完全气体没有考虑气体组分的化学反应,仅考虑了流场的输运作用,因此摩擦位置在马赫数为16~22的速度区间内几乎不发生迁移。反之,等离子体气体考虑了化学平衡的改变,等离子体热力学性质的改变以及流场的输运,随着流速的提高,不同组分的流体黏度逐渐发生改变,摩擦位置逐渐向钝体中部迁移。
由图4(f)可见,黏性力在222 mm处的变化较为显著,由图4(e)可见,等离子体模型的计算结果表明,摩擦环较平滑且数值增大了611.8%,表明了等离子体气体模型所计算的混合物黏性力更大。
3.2 再入流固耦合应力分析
飞行器在高速运动时,真实气体效应对其受荷状态影响较大。研究真实气体的流固耦合作用对于正确计算飞行器受荷状态有重要的意义。流体荷载所引起的流固耦合应力虽不如热作用引起的应力大,但其对飞行器受荷状态有着多方面的耦合影响。飞行器外部材料为钢,其弹性模量为200 GPa,泊松比为0.30,外壳厚度为40 mm。
通过计算得到了Ma=22下热完全气体和等离子体下的再入飞行器外部结构钢壳的应力场,图5(a)为飞行速度Ma=22下等离子体流固耦合应力σMises的分布云图,图5(b)为飞行速度Ma=22下热完全气体流固耦合应力σMises的分布云图。

图5 流固耦合作用下飞行器的Mises应力Fig.5 Mises stress of aircraft under fluid structure coupling
由图5可见,等离子体流固耦合应力与热完全气体流固耦合应力的分布相似,这与飞行器上的荷载主要是气动压力有关,等离子体气动压力与热完全气体气动压力作用形式和作用大小相似。从数值大小上分析,等离子体流固耦合应力比热完全气体流固耦合应力在Ma=22下的最大值小9.5%,这是由于等离子体气动压力更为集中的作用于飞行器尖端,其冲击环可近似是为一个冲击点,而热完全气体气动压力更集中作用在飞行器头部靠近尖端的冲击位置上。计算结果证明,等离子体气动作用虽然较大,但实际造成的Mises应力更小。
3.3 不同等离子体组分的流固耦合作用
由于等离子体是由多种组分混合而成的混合物,流固耦合作用也可以分解为不同等离子体组分的作用,不同组分在壁面上的组分质量分数显示了壁面承受组分作用的贡献。对再入飞行器壁面的等离子体组分分析,如图6所示。
随着马赫数的增加,图6(a)中壁面氧分子质量分数逐渐减小,至Ma=22时大部分离解。图6(b)中,壁面氧原子质量分数逐渐增加,至Ma=22基本覆盖飞行器前端。图6(c)中壁面氮分子质量分数逐渐减小,至Ma=22时,飞行器前端基本离解完毕,中后端质量分数较大,离解程度逐渐减弱。图6(e)中NO作为N与O的结合生成物,同时也是电子与NO正离子的反应物,在Ma=16时质量分数较高,在Ma=22时质量分数较低。由图6(f)和图6(g)可见,电子和NO正离子的质量分数逐渐增大。
图7为不同来流速度下壁面气体的热力学温度。由图7可见,随着来流马赫数的增加,再入飞行器流固边界热力学温度逐渐上升,导致图6中流固边界的空气发生了多种等离子体反应。再入飞行器承受的冲击粒子由氧气和氮气转为承受氧原子和氮原子。这意味着此时飞行器承受流固耦合作用的物质不同。
以马赫数22来流下的再入飞行器壁面物种而言,结合3.1节得到的马赫数22来流速度下的再入飞行器壁面流固耦合作用,如图8所示:在弧长0~200 mm的位置上,O2已充分反应为O,氮气也充分反应为N,少部分O与N发生结合生成NO,飞行器尖端主要承受来自这3种物质组成的原子气体的冲击和摩擦;在弧长200~400 mm的位置上,即飞行器中后部,随着温度的减小和流场对于O与N的输运,发生了化学平衡的逆向移动,此时O与N又生成了O2与N2,这部分壁面上主要承受O2与N2组成的分子气体的冲击和摩擦。对于电子与NO正离子组成的等离子体,由于主要反应物NO的生成量较少,该部分气体对于壁面的冲击和摩擦可以忽略,从图8中可以看出二者质量分数分布的一致性,从侧面检验了模型的计算正确性。
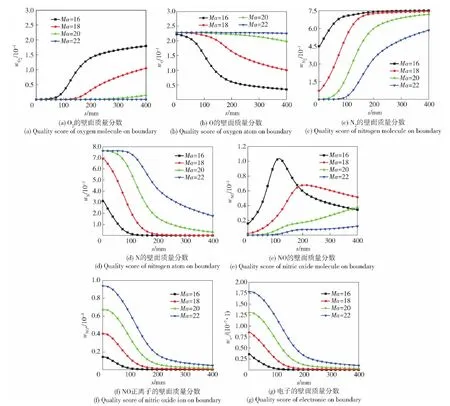
图6 不同速度下等离子体组分壁面分布Fig.6 Distribution of plasma components on the wall at different velocities
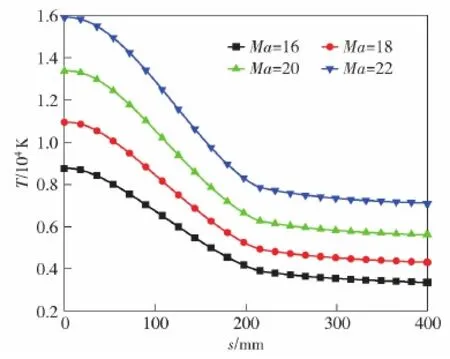
图7 不同速度下的壁面热力学温度Fig.7 Wall thermodynamic temperature at different velocities
3.4 真实气体效应对流固耦合的影响
并非所有飞行器都在高温条件下工作,对于低速飞行器,来流空气几乎不发生化学反应,热力学性质和输运性质较为稳定,使用热完全气体模型可以得到比较精确的结果。随着速度的增大,真实气体效应对飞行器的影响将逐渐加强。
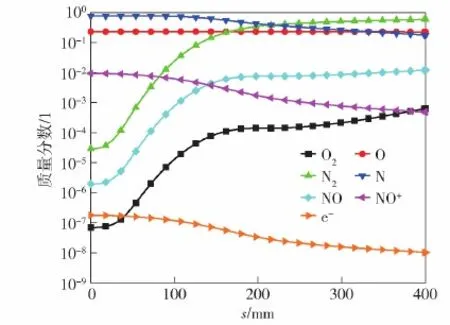
图8 Ma=22等离子体壁面分布Fig.8 Plasma distribution on boundary in Ma=22
图9(a)为飞行器尖端的物种变化,图9(b)为飞行器尖端的气动荷载变化与两个气体模型的差异。由图9(a)可知,当飞行器的速度升至马赫数5时,振动能量被激发,此时氧原子开始生成,马赫数5后需要使用真实气体模型才能准确描述真实气体中各个组分对飞行器的影响。由图9(b)可知,等离子体与热完全气体间的相对差异在马赫数5后趋于稳定。
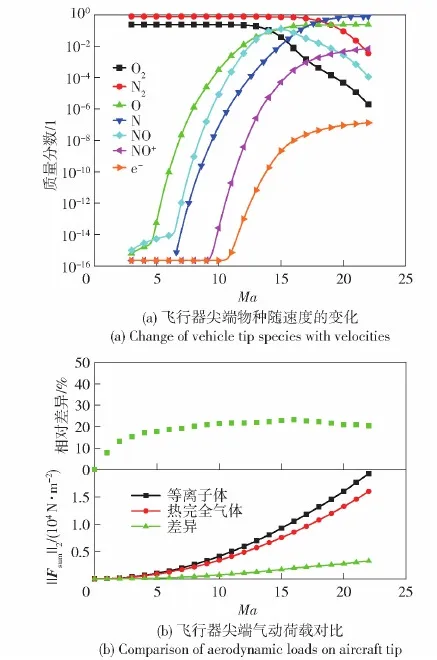
图9 等离子体气动荷载影响Fig.9 Influence of plasma aerodynamic load
4 结论
本文对等离子体关于再入飞行器的流固耦合作用做了分析,并与热完全气体流固耦合作用进行对比,探讨了高超声速飞行器在等离子体中穿行所承受的流固耦合作用。得出以下主要结论:
1) 等离子气体相较于热完全气体,由于考虑等离子体真实气体效应,产生的最大气动压力更大,在马赫数22的高速来流下增大了16.5%,黏性力增大了611.8%。
2) 等离子气体相较于热完全气体,最大冲击和摩擦位置将会改变,热完全气体在来流速度逐渐增大的过程中,该位置几乎不变,而等离子体的最大摩擦位置会向钝体中部移动,表明了高超声速飞行器考虑真实气体效应的流固耦合作用最大值位置将发生迁移。
3) 高超声速飞行器不同位置承受的冲击和摩擦物质不同,随着来流马赫数的增大,等离子体组分分布动态改变,在小于马赫数20的速度下,等离子体反应温度不够,冲击和摩擦物质主要为O2与N2。在马赫数为20~22的速度下,冲击物质由分子向原子转变。在马赫数22的来流速度下,冲击物质主要为O与N,还存在有少量NO,此时还有极少数的NO正离子和电子。以马赫数22来流速度下的壁面为例,飞行器顶部承受原子气体作用,中后部承受分子气体作用,表明化学非平衡对流固耦合机制影响较大,将导致流固耦合作用物质分布的不同。
4) 当飞行器速度超过马赫数5时,气体振动能被激发,等离子体在描述气体热力学和化学状态上更准确,在计算时必须考虑到这一差异。
