基于非线性黏滞阻尼器的输电塔减震控制研究

李健

（厦门绿发投资有限公司，厦门 361001）

0 引 言

输电塔是国家电网“西电东送”战略中的重要电力能源基础设施，属于高柔性结构，高度较高，自振周期较长，阻尼比较小，对风荷载和地震动等外界动力作用较为敏感［1-2］。在极端情况下，风荷载和地震动甚至会导致输电塔发生屈曲倒塌，造成不良社会影响和重大经济损失。虽然输电塔结构在数值模拟、理论分析和试验研究方面均取得了一些进展［3-5］，但输电塔的减震控制仍是目前的研究热点。

输电塔减振控制一般可分为主动控制、半主动控制和被动控制。被动控制主要采用基础隔振、吸能减振、耗能减振等措施来减小结构的动力响应。耗能减振技术主要通过在受控结构变形较大处设置阻尼单元耗散输入能量，从而达到抑制结构振动的目的，主要包括黏滞阻尼器、摩擦阻尼器、SMA阻尼器等。郭勇等［6］提出了一种混合遗传算法用于输电塔阻尼器的多目标优化布置，结果表明该算法可以有效控制输电塔的风振响应，同时减少了需要安装的阻尼器数量。钟万里等［7］基于数值模拟软件ANSYS分析了黏弹性阻尼器对塔架结构的风振控制效果，将黏弹性阻尼器布置于输电塔中上部主材处，台风作用下的振动加速度下降60%～70%。Matsumoto等［8］研究了黏滞阻尼器的布置形式和阻尼系数对输电塔减震效果的影响，结果表明黏滞阻尼器可以有效降低塔顶位移响应，并且建议对黏滞阻尼器进行优化设计以达到最优控制效果。Huang等［9］开展了输电塔风振控制中的黏弹性阻尼器优化研究，结果表明与阻尼器连接的钢支撑刚度对有控输电塔的最大附加阻尼比有很大影响，同时黏弹性阻尼器的安装位置对控制效果影响也比较大，黏弹性阻尼器对塔顶位移和横向弯曲振动能有最好的控制效果。Letícia等［10］利用回溯搜索优化算法开展了摩擦阻尼器在输电塔减震控制中的多目标优化研究，同时得到摩擦阻尼器的最优布置位置及最优摩擦力，结果表明仅用3个摩擦阻尼器便可使最大塔顶位移降低55%。Chen等［11］建立强震作用下安装摩擦阻尼器的输电塔动力运动方程，开发了输电塔线体系的能量响应评估方法，并研究了摩擦阻尼器控制力、刚度和安装位置对减震效果的影响，结果表明摩擦阻尼器可以很好地抑制输电塔线体系的地震响应。Zhan等［12］提出了一种具有复位功能的可变摩擦阻尼器，并对受控下输电塔架模型开展了振动台试验，验证了装置的有效性。张春蕊和张发［13］开展了SMA阻尼器对输电塔风致振动的控制研究，结果表明SMA阻尼器布置在塔头时，塔顶位移减振率大于28%；SMA阻尼器布置在塔身时，塔顶加速度减振率大于66%。李健［14-15］研究了近场罕遇地震作用下干字型输电塔的动力响应，并利用SMA阻尼器对其进行减震控制，结果表明不同地震波作用下的减震效果具有较大差异性，塔顶位移的减震效果最好。Wu等［16］将SMA阻尼器用于电视塔结构的减震控制，分别从时域和频域分析了结构动力响应的减震效果，研究了SMA阻尼器刚度、工作温度和地震强度对控制效果的影响，结果表明SMA阻尼器可以有效降低电视塔的振动响应。Chen等［17］提出了基于SMA阻尼器的输电塔线体系风振控制方法，研究了各种参数对结构动力响应和阻尼器滞回曲线的影响规律，并通过能量响应分析验证了风致动力响应的控制效果。

综上所述，输电塔架结构在被动控制领域的研究较为成熟，由于具有无需外界能量输入、稳定性较高等特点，被动控制技术已在很多实际应用中取得了良好的控制效果，成为输电塔减振控制的主要研究方向。由于黏滞阻尼器是一种无刚度的速度型阻尼器，可以在几乎不产生附加刚度及附加质量的同时提供额外的附加阻尼，阻尼力-位移滞回曲线饱满，具有稳定的动力特性和很强的耗能能力。目前，黏滞阻尼器已广泛应用于输电塔结构的风振控制，而在地震作用下的输电塔减震控制研究较少。同时，应用于输电塔减震控制的黏滞阻尼器多集中于线性阻尼器方面，减震效果受到一定的限制，非线性黏滞阻尼器的开发、设计与应用尚有一定的研究空间。

为研究黏滞阻尼器对输电塔减震控制效果的影响，本文利用SAP2000建立了输电塔三维有限元模型，采用Damper Exponential连接模拟速度型黏滞阻尼器，分析了黏滞阻尼器安装位置、速度指数、阻尼系数对输电塔峰值动力响应、阻尼器滞回曲线和能量耗散特征的影响规律，从而为非线性黏滞阻尼器在输电塔减震控制中的应用提供借鉴。

1 输电塔有限元模型及动力时程分析

干字型输电塔的三维有限元模型见图1，杆材和主斜材采用框架截面模拟（Q420钢材和Q345钢材），辅助连接杆材采用Linear连接模拟（Q235钢材），框架截面形状均为L形。钢材弹性模量为2.1×1011Pa，泊松比为0.3，密度为7 850 kg/m3。

图1 输电塔有限元模型Fig.1 Finite element model of transmission tower

FVD是一种速度相关型的耗能装置，利用液体的黏性提供阻尼来耗散风、地震、移动荷载等输入的振动能量。黏滞阻尼器由外筒、活塞、黏滞流体、导杆等组成，筒内充满黏滞流体，活塞可在筒内进行往复运动，活塞上开有适量小孔或活塞与缸筒留有空隙（图2）。筒内黏滞流体一般采用惰性、不易燃、无毒、环保安全、热稳定的可压缩硅油，当结构在风荷载或地震作用下产生变形时，外筒和活塞将产生相对运动，迫使硅油从小孔或间隙流过，通过产生的阻尼力达到黏滞耗能目的。

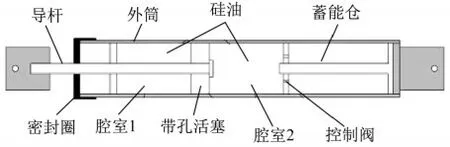
图2 黏滞阻尼器剖面图Fig.2 Profile of fluid viscous damper

在地震和风等外界低频振动激励下，可忽略黏滞阻尼器的刚度影响项，《建筑消能减震技术规程》（JGJ 297—2013）及多数有限元模拟软件（Sap2000、Midas、Etabs、Abaqus等）均采用以下模型来描述黏滞阻尼器的力学特性：

式中：Fd为阻尼器输出的阻尼力；Cα为阻尼系数，表示阻尼器的能量耗散能力，与外筒直径、活塞直径、导杆直径和流体黏度等因素有关；α为速度指数，与阻尼器内部构造有关为符号函数，为阻尼器两端的轴向相对速度。

对于安装有黏滞阻尼器的输电塔结构，其运动方程可以表示为：

其中：M、C、K分别为输电塔结构的质量、阻尼和刚度矩阵；u（t）为位移响应列向量；Fd（t）为阻尼器输出的阻尼力列向量；I为单位列向量为地震加速度。

为了研究黏滞阻尼器的耗能效果，本文对无控和有控输电塔进行能量响应分析，通过对动力运动方程进行积分，可以得到无控输电塔的能量方程为

有控输电塔的能量方程为

式中：ET为地震动输入的总能量；EKE为结构系统的动能；EDE为结构系统的阻尼耗能；ESE为结构系统的势能；EHE为黏滞阻尼器的滞回耗能。

EKE和ESE只参与能量的相互转换，并不参与能量耗散，因此无控输电塔主要依靠结构自身阻尼来耗散输入的地震能量，而有控输电塔可以同时依靠结构自身阻尼和黏滞阻尼器进行耗能。

本文选用El Centro地震波（RSN6，水平分量180）进行有控和无控输电塔的动力时程分析，由于输电塔第一阶振动模态为Y向弯曲振动，故地震作用激励方向设为输电塔结构模型的Y向，地震波相关信息及加速度时程数据可在太平洋地震工程研究中心（PEER）网站（https：//ngawest2.berkeley.edu/）根据RSN编号进行下载，如图3所示。为了研究黏滞阻尼器安装位置对输电塔减震控制效果的影响，本文分别在输电塔模型Y向前后两侧各安装4个黏滞阻尼器（共8个），沿输电塔高度方向设置三种不同的安装方案，方案1安装在输电塔底部，方案2安装在输电塔中部，方案3安装在输电塔顶部，如图4所示。

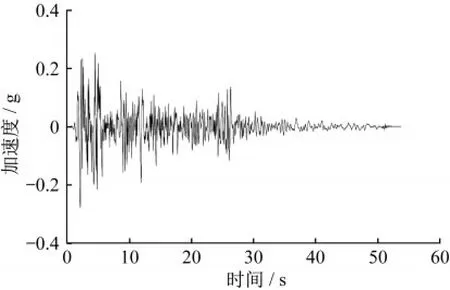
图3 El Centro地震波加速度时程Fig.3 Time histories of El Centro waves

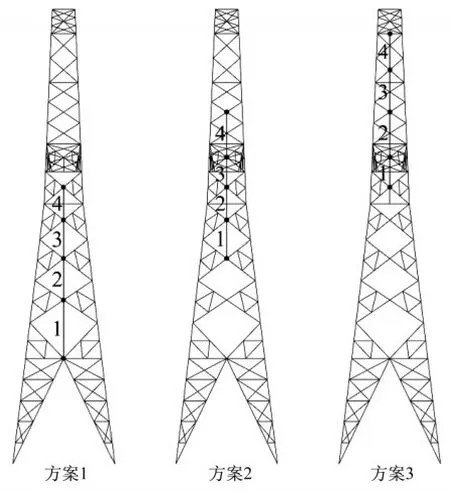
图4 黏滞阻尼器安装方案Fig.4 Installation schemes of FVDs

在非线性动力时程分析中，输电塔结构阻尼采用瑞利阻尼，第1阶和第3阶模态的阻尼比均设为0.01，黏滞阻尼器采用Damper Exponential连接模拟，动力时程分析步长取0.01 s。本文采用减震率（VRR，Vibration Reduction Ratio）来评价黏滞阻尼器对输电塔结构的减震控制效果：

式中：R0和RC分别为无控和有控输电塔结构的动力响应；后续章节中分别用VRRd、VRRv、VRRa表示输电塔塔顶峰值位移、速度和加速度的减震率，用VRRe表示输电塔地震输入能量的减震率。

2 阻尼器安装位置对减震效果的影响

考虑图4中的三种安装方案，设置速度指数α为1.0，阻尼系数Cα为5×104N/（m·s-1），分别进行有控和无控输电塔结构的非线性动力时程分析，表1为采用不同安装方案时输电塔塔顶峰值响应的减震率。由表1可知，采用安装方案1时，黏滞阻尼器具有一定的减震控制效果，随着阻尼器安装高度逐渐增加，减震控制效果不断减弱。当采用安装方案3时，黏滞阻尼器基本没有发挥耗能作用，峰值响应减震率几乎为零。三种不同安装方案中阻尼器滞回曲线均近似于椭圆形，方案1中的阻尼器轴向位移和阻尼力最大，方案3中的阻尼器轴向位移和阻尼力最小。

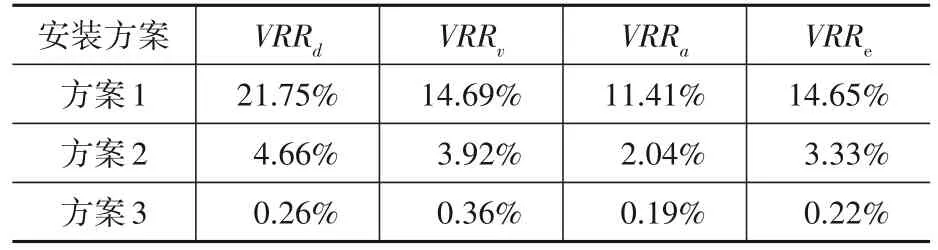
表1 不同阻尼器安装方案下的输电塔塔顶峰值响应减震率Table 1 Vibration reduction ratio of peak response under different installation schemes%

由图4可知，在Y向地震作用下，输电塔底部受力较大且1号阻尼器两端距离较长，因此两端轴向相对速度较大，可以充分发挥阻尼器的减震控制效果。由于方案1中的4号阻尼器耗能较少，考虑到输电塔减震控制的经济性，将其从安装方案1中删除，仅设置1～3号阻尼器（输电塔两侧共6个阻尼器）。对于优化后的阻尼器安装方案1重新进行动力时程分析，塔顶峰值位移、速度、加速度的减震率分别为21.75%、14.66%、11.38%，地震输入能量减震率为14.63%，整体减震效果基本保持不变。

由于无法事先确定地震作用方向，实际工程中可将黏滞阻尼器按照优化方案1分别布置在输电塔的X向和Y向，从而有效抑制输电塔结构的峰值动力响应。为了减小计算量并控制论文篇幅，本文后续章节中仍以输电塔Y向为地震激励方向进行非线性黏滞阻尼器的参数化分析。

3 黏滞阻尼器非线性参数对减震控制效果的影响

3.1 速度指数对减震控制效果的影响分析

根据优化后的黏滞阻尼器安装方案，设置黏滞阻尼器的阻尼系数Cα=5×104N/（m·s-1），速度指数α分别设置为1.0、0.5和0.3，在El Centro地震波激励下进行非线性动力时程分析，研究速度指数对输电塔减震控制效果的影响机制。图5给出了不同速度指数下的1号黏滞阻尼器滞回曲线，可以发现随着速度指数的不断减小，阻尼器的最大轴向位移不断减小，最大阻尼出力不断增加，滞回曲线由椭圆形逐渐过渡到近似矩形，阻尼器的耗能能力不断增强。无控输电塔结构的地震输入能量全部由结构自身阻尼耗散，有控输电塔结构的地震输入能量则由结构自身阻尼和阻尼器滞回变形来耗散，如图6所示。随着速度指数由1.0减小到0.3，阻尼器滞回耗能的比例逐渐增大，输电塔结构的地震输入能量逐渐减小，而且地震输入能量曲线变得更加光滑，说明输电塔结构的动能和势能得到了有效抑制。图7给出了输电塔结构在不同速度指数下的动能响应，可以发现结构动能响应随速度指数的减小而逐渐减弱。输电塔结构的势能响应也有类似变化规律，由于篇幅限制本文不再赘述。

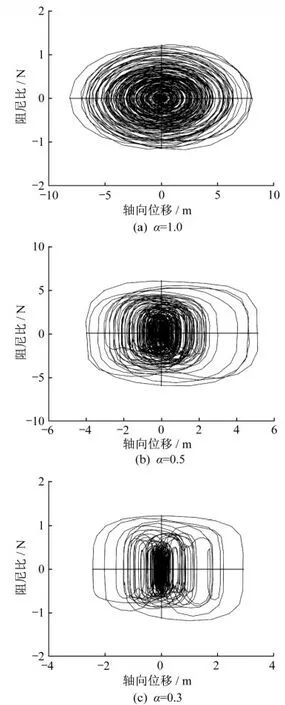
图5 有控输电塔1号阻尼器滞回曲线Fig.5 Hysteretic curve of No.1 FVD of controlled tower

图6 输电塔在不同速度指数下的耗能特征Fig.6 Energy dissipation characteristics of transmission tower

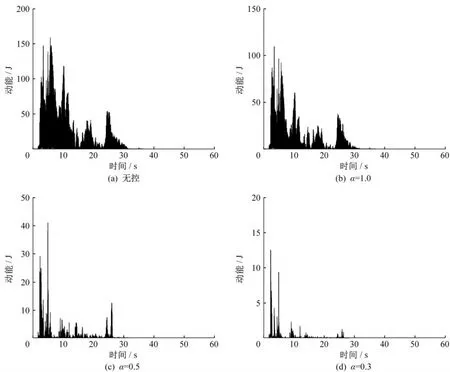
图7 输电塔在不同速度指数下的动能响应Fig.7 Kinetic energy response of transmission tower

3.2 阻尼系数对减震效果的影响分析

根据优化后的黏滞阻尼器安装方案，设置黏滞阻尼器的速度指数为1.0，阻尼系数分别设为λCα，其中缩放倍数λ=0.5、1.0、2.0、3.0，在El Centro地震波激励下进行非线性动力时程分析，研究阻尼系数对输电塔减震控制效果的影响机制。图8给出了不同阻尼系数λCα下的1号黏滞阻尼器滞回曲线，可以发现随着阻尼系数的不断增大，阻尼器的滞回曲线仍然保持椭圆形，最大阻尼出力近似呈线性增加，最大轴向位移不断减小，但是减小幅度有限。图9给出了有控输电塔结构能量响应随阻尼系数的变化规律，可以发现随着缩放倍数从0.5增加到3.0，结构阻尼耗能逐渐减小，阻尼器滞回耗能不断增大，但是地震输入能量的减小幅度不明显。相较于速度指数对输电塔结构耗能的影响规律，随着阻尼系数的不断增大，地震输入能量曲线并没有趋于光滑，说明增大阻尼系数并未很好地抑制输电塔结构的动能和势能响应。图10给出了输电塔结构在不同缩放倍数下的动能响应曲线，可以发现结构动能响应没有大幅降低，势能响应也有类似变化规律，由于篇幅限制本文不在赘述。

图8 有控输电塔1号阻尼器在不同阻尼系数下的滞回曲线Fig.8 Hysteretic curves of No.1 FVD of controlled tower under

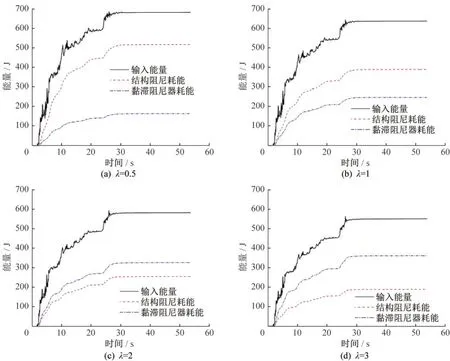
图9 有控输电塔在不同阻尼系数下的耗能特征Fig.9 Energy dissipation characteristics of controlled tower under

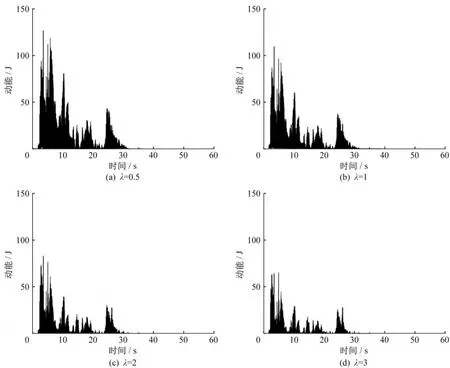
图10 有控输电塔在不同阻尼系数下的动能响应Fig.10 Kinetic energy response of controlled tower under

3.3 速度指数和阻尼系数的综合影响分析

为了更加全面地研究速度指数和阻尼系数对输电塔塔顶峰值响应和地震输入能量的综合影响，速度指数α设置为1.0、0.5、0.3，阻尼系数设置为λCα（λ=0.5、1.0、2.0、3.0），在El Centro地震波激励下进行参数化分析。

图11～图13分别给出了不同参数组合下的输电塔塔顶位移峰值、速度峰值和加速度峰值的减震率。对比分析图11（a）和图11（b）可知，图11（a）中的曲线近似直线，输电塔塔顶位移峰值减震率VRRd与速度指数α近似呈线性关系。图11（b）中的曲线在速度指数较大时（α=0.5、1.0）与缩放倍数近似呈线性关系，但当速度指数较小时（α=0.3）曲线先上升后趋于平缓。图11（a）中的阴影面积小于图11（b）中的阴影面积，表明相对于增加阻尼系数，减小速度指数可以更加有效地提高减震率。对于输电塔塔顶速度峰值和加速度峰值的减震率，也存在相同的影响规律，如图12和图13所示。

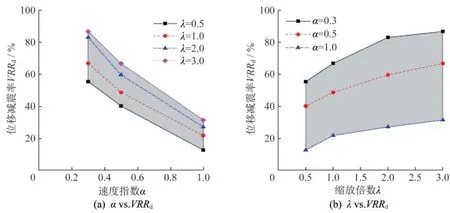
图11 输电塔塔顶位移峰值减震率Fig.11 VRR of peak displacement at tower top

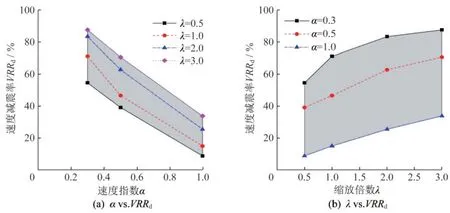
图12 输电塔塔顶速度峰值减震率Fig.12 VRR of peak velocity at tower top

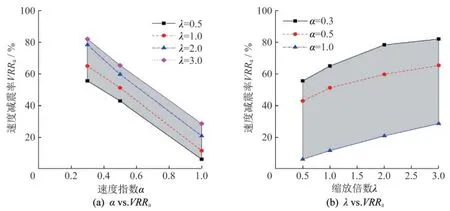
图13 输电塔塔顶位移减震率Fig.13 VRR of peak acceleration at tower top

图14给出了不同参数组合下输电塔输入能量的减震率，可以发现当速度指数大于0.5时，输入能量的减震率随阻尼系数的增加呈线性增大趋势，而当速度指数为0.3时，输入能量的减震率呈现更加明显的非线性增加趋势。同样，减小速度指数比增加阻尼系数对于提高输入能量减震率更加有效，而且具有更好的经济性，因为阻尼系数与外筒直径、活塞直径、导杆直径和流体黏度等因素有关。

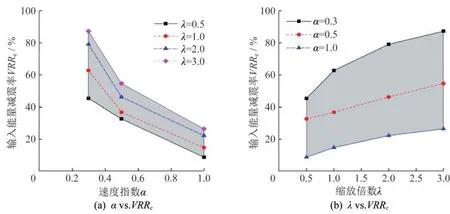
图14 输电塔结构地震输入能量减震率Fig.14 VRR of seismic input energy

4 结 论

本文利用SAP2000建立了输电塔结构的三维有限元模型，采用Damper Exponential连接模拟非线性黏滞阻尼器的力学性能，研究了黏滞阻尼器安装位置（方案1～3）、速度指数α（1.0、0.5、0.3）、阻尼系数（λCα，λ=0.5、1.0、2.0、3.0）对输电塔峰值动力响应、阻尼器滞回曲线和结构能量耗散特征的影响规律，主要结论如下：

（1） 针对本文所研究的输电塔结构形式，在塔身底部安装黏滞阻尼器可以充分发挥其减震控制效果。考虑到输电塔减震控制的经济性原则，可在输电塔塔身底部四周由下至上各设置3个黏滞阻尼器。

（2） 当阻尼系数保持不变时，随着速度指数的不断减小，黏滞阻尼器的最大轴向位移不断减小，最大阻尼出力不断增加，滞回曲线由椭圆形逐渐过渡到近似矩形，阻尼器的耗能能力不断增强。同时，输电塔结构的地震输入能量明显减小并变得越来越光滑，输电塔结构的动能和势能得到了有效抑制。

（3） 当速度指数保持不变时，随着阻尼系数的不断增大，黏滞阻尼器的滞回曲线保持椭圆形，最大阻尼出力近似呈线性增加，最大轴向位移小幅减小。同时，输电塔结构的地震输入能量缓慢减小，且地震输入能量曲线仍然波动剧烈，输电塔结构的动能和势能未能得到有效抑制。

（4） 综合考虑速度指数和阻尼系数对输电塔减震控制效果的影响，减小速度指数比增加阻尼系数在减震效果和经济性方面更具有优势，在实际工程项目中应优先考虑。