关注“学生理解” 提升数学素养
2023-11-25陶炳宏
陶炳宏
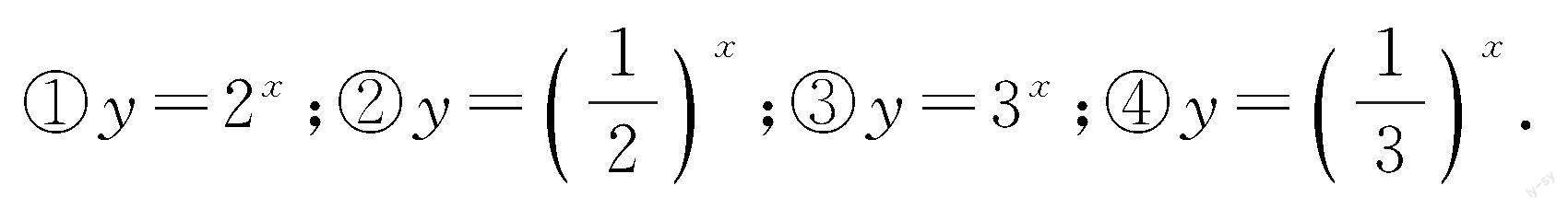
摘要:课堂教学应立足于学生的已有认知结构,增强学生理解力的培养.教学设计应以学生理解为根,以学生理解能力发展为线,营造有利于学生理解力发展的学习氛围,关注学生主体性的激发,以此带领学生走向理解之路.
关键词:课堂教学;教学设计;学生理解
在高中数学教学中,教师应以发展学生为目标,引领学生经历自主探究和合作交流等学习活动,让数学课堂由“关注教学内容”向“引领学生理解”转变,深化学生对数学本质、思想方法、人文精神的理解,以此提高学生理解力和学生数学素养,培养学生全面发展、可持续发展的能力[1].笔者从课堂教学目标、教学内容、教学活动及教学评价四个方面浅谈对提高学生理解力,发展学生数学素养的几点拙见,若有不足,请指正!
1 教学目标的设定应关注学生的理解
众所周知,课堂教学的主体是学生.教师在设定教学目标时应充分关注学生的主体性,关注学生的需求,关注学生的理解,以确保教学目标切实服务于学生,促进学生学习能力和数学素养的提升[2].
案例1 “弧度制”教学目标的设定
(1)通过经历数学史的演变过程引入相关定义,掌握弧度的概念,理解1弧度的角,明确引入弧度制的必要性;
(2)通过对比分析,挖掘角度与弧度的内在联系,掌握角度与弧度的换算公式,并能够灵活应用公式完成相应的换算;
(3)通过角的度量,体会角度制与弧度制的区别与联系,理解角度制与弧度制之间的互化;
(4)体会知识之间的联系,理解不同表象下的相同的本质,发展学生发现、分析和解决问题的能力.
由角度制到弧度制,是对学生认知结构的一次调整,也是对学生的一次挑战.受原有认知结构的干扰,学生在学习过程中可能会遇到一些障碍.若教学中仅是讲授,不带学生去经历,学生对知识的理解可能一知半解,这样势必会影响学生的学习信心和学习兴趣.因此,在教学中,应引导学生经历弧度制的形成和发展过程,让学生理解引入弧度制的合理性、科学性与必要性,以此通过亲身经历提高课堂教学的实效性.同时,在本课教学中,应重视引导学生对比角度的认知过程,做好知识的“同化”与“顺应”,让学生在理解的基础上学习运用,提高课堂教学效率.
2 教学内容的设置应符合学生的认知水平
在应试教育的束缚下,部分教师对数学教学存在一些片面的认识,认为高考题新、难.为了让学生适应高考,教师在教学内容的选择上常常求新、求难,而这样的教学内容并不适合学生的现有认知水平,才使课堂上出现“冷场”和“强灌”等情况,影响学生数学学习信心,不利于学生长远发展.因此,在高中数学教学中,应立足学生已有知识结构,选择利于激发学生学习兴趣、利于培养数学思维能力、体现数学人文价值和育人功能的教育内容,以此提高学生参与课堂的积极性和主动性,逐步提高学生的数学水平[3].
案例2 “函数y=Asin(ωx+φ)”的图象
教学中,若直接通过讲授让学生理解和记忆,势必会出现理解障碍,影响教学效果.分析教学内容不难发现,由“y=sin ωx”到“y=sin(ωx+φ)”是教学的一个难点.为了突破这一难点,可从学生已有认知水平出发,设置如下问题:
(1)函数y=x的图象经过何种变换可得到函数y=x+1的图象?
(2)函数y=2x的图象经过何种变换可得到函数y=2x+1的图象?
(3)函数y=4x2的图象经过何种变换可得到函数y=(2x+1)2的图象?
(4)函数y=sin 2x的图象经过何种变换可得到函数y=sin(2x+1)的图象?
(5)函数y=f(ωx+φ)(ω>0)的图象经过何种变换可得到函数y=f(ωx)(ω>0)的图象?
在设计教学内容时,从学生熟悉的一次函数和二次函数出发,让他们充分体会图象变换,为接下来探究三角函数图象的平移变换提供依据.以上教学内容的设计遵循由简入繁、由特殊到一般的逻辑发展规律,符合学生的认知水平发展特点.这样不仅可以激发学生探究热情,而且可以帮助学生更好地理解知识,有利于提高独立思考和自主探究能力,聚焦数学本质,促进深度学习.
3 教学活动的设计应突出学生的主体性
在传统数学教学中,部分教师过度强调“教”的价值,而忽视了“学”的重要性,常常将教师的“教”放在学生的“学”之前,从而使课堂因为缺少学生的积极参与而变得枯燥乏味.为了改变这一局面,教师应更新教学观念,以发展学生为目标,以学生的学习活动为重心,围绕学生的“学”设计教学活动,以此帮助学生更好地理解和掌握知识.同时,教学中,教师要为学生搭建理解的平台,鼓励学生去思考、去发现、去合作、去质疑、去讨论,通过经历知识的形成过程,促进对数学内容的理解.
案例3 “空间等角定理”教学活动设计
在研究“空间等角定理”时,首先让学生思考:平面内,如果∠BAC与∠B′A′C′的边AB∥A′B′,AC∥A′C′,且边AB与A′B′方向相同,边AC与A′C′的方向也相同,那么这两个角存在怎样的关系?该结论在空间成立吗?
学生结合已有经验,判断∠BAC与∠B′A′C′相等.在此基础上,学生通过“想一想”“画一画”和“猜一猜”等活动,猜想该结论在空间同样成立,由此得到空间等角定理.接下来,鼓励学生结合图形“证一证”.在教师的启发和引导下,学生结合图形写出已知、求证及证明过程.为了深化学生对新知的理解,于是引入如下问题让学生“议一议”:如果∠BAC与∠B′A′C′的边AB∥A′B′,AC∥A′C′,且边AB与A′B′方向相同,而AC与A′C′的方向相反,那么∠BAC与∠B′A′C′之间有何关系?说一说你的理由.
在以上教学活动中,教师从学生已有认知出发,从平面迁移至空间,通过经历“想一想、猜一猜、证一证、议一议”等活动,引领学生主动参与等角定理的猜想、证明及应用过程,使得探究能力和思维能力在潜移默化中得到发展和提升.以上教学中,教师将主动权交给学生,给学生足够的空间和时间参与到知识的形成和发展过程中,促进自主学习能力的提升.同时,也重视对学生合作能力的培养,在“证一证、议一议”活动中,鼓励学生合作交流,以此通过师生和生生的有效沟通使教学内容更加丰富化、立体化.
4 教学评价应以发展学生理解力为导向
当前,在素质教育的推动下,课堂教学评价要打破单一的教师评价方式,将学生互评和个体自评落到实处,以此通过全方位的评价发展学生的问题理解能力,提高课堂教学的有效性.
案例4 “指数函数的图象与性质”教学评价设计
(1)运用描点法在同一直角坐标系中画出如下指数函数的图象:
(2)展示学生作品,并运用几何画板作出相应的指数函数图象;
(3)观察图象,总结归纳图象特征和函数性质;(小组讨论)
(4)各小组派一名代表汇报探究结果;
(5)师生共同整理和归纳.
结合以上教学活动,教师设计如下评价要点:
(1)关注学生是否能够正确画出以上4个指数函数的图象;
(2)結合函数图象,关注学生是否能够用自己的语言描述图象的特征;
(3)关注学生是否能够灵活运用研究其他函数性质的方式来研究指数函数;
(4)关注学生学习过程的评价,重点观察学生参与小组合作的积极性和主动性.
在教学评价过程中,教师应以组织者、启发者和合作者的身份融于课堂,关注学生的兴趣点、障碍点,通过有效的启发与引导点燃学生智慧之火,引发学生积极思考.在评价过程中,要改变教师一人评价的局面,通过经历独立思考和合作探究等活动引导学生互评和自评,以此通过评价的多样化激发学生数学学习热情,促进学生学习能力的全方位发展与提升.
总之,教师在教学设计的过程中,应以学生理解为出发点,围绕促进学生的理解来设计,充分发挥学生的主体价值,让学生通过自主探究和合作探究等活动更好地理解知识,发展能力,提升素养.
参考文献:
[1]徐海兵.以学生主体为出发点的高中数学教学研究[J].新课程导学,2016(8):75.
[2]冯俊.以学生培养为出发点的高中数学教学途径[J].课程教育研究,2018(41):131-132.
[3]刘苹.核心素养视角下高中数学高效课堂的构建[J].高考,2019(12):110.
