一种改进的小波阈值去噪算法

侯云海, 任 钰

(长春工业大学 电气与电子工程学院, 吉林 长春 130012)

0 引 言

电力设备在产生局部放电现象时会造成设备的绝缘劣化,放电严重时会击穿绝缘层,引起设备局部位置温度升高,有产生火灾的潜在可能。在这种背景下检测电力设备绝缘性能很有必要,对局部放电现象进行实时监测是一种当下较受欢迎的绝缘诊断方法[1]。局部放电检测方法主要有脉冲电流、特高频、超声波、光测法等[2]。

电力设备通常位于干扰信号较强的环境中,在进行局部放电在线监测时容易受干扰信号的影响,致使在采集到的信号中难以将原始信号准确识别出来。干扰信号通常包含白噪声、周期噪声和脉冲干扰,其中白噪声成为主要干扰源的情况最为常见。针对局部放电中白噪声过滤的方法主要有卡尔曼滤波器[3]、经验模态分解[4-5]和小波阈值去噪[6-7]等方法。

局部放电信号是一种微弱的暂态信号,极易受到干扰,所以传统的滤波方法难以有效处理含噪的局部放电信号,降噪后的信号也难以保留原始信号的特征。小波阈值去噪法作为一种近年来发展起来的信号处理工具,在信号处理、图像处理以及故障检测等方面得到广泛使用。

在去噪的方法选择上,最早提出采用硬阈值以及软阈值这两种去噪方法[8]。然而,传统软、硬阈值函数在数学表达式上有缺陷,文中在充分吸取以上两种优化函数优势的基础上,提出一种改进的阈值函数,经过模拟仿真降噪实验,分析实验结果,证实了改进函数较以往函数的去噪优化上有明显提升。

1 小波阈值去噪原理

小波阈值去噪算法依据的原理是[9]:带有干扰噪声的信号经过小波分解后,要提取保留信号的能量主要汇集在小波系数幅值较大的区域,而干扰信号的能量主要分布在小波系数幅值较小的区域。因此,可以通过对阈值设定适切的判定门限作为分解后小波系数保留与否的判定准则。

具体操作过程是将小于判定门限阈值的小波系数作为干扰信号的小波系数,将其滤除,剩下的系数作为有效信号的小波系数。采用一定的规则将视作有效部分留存的小波系数逆变换,重组出的信号即视作滤除杂波后的去噪信号。小波阈值去噪算法流程如图1所示。

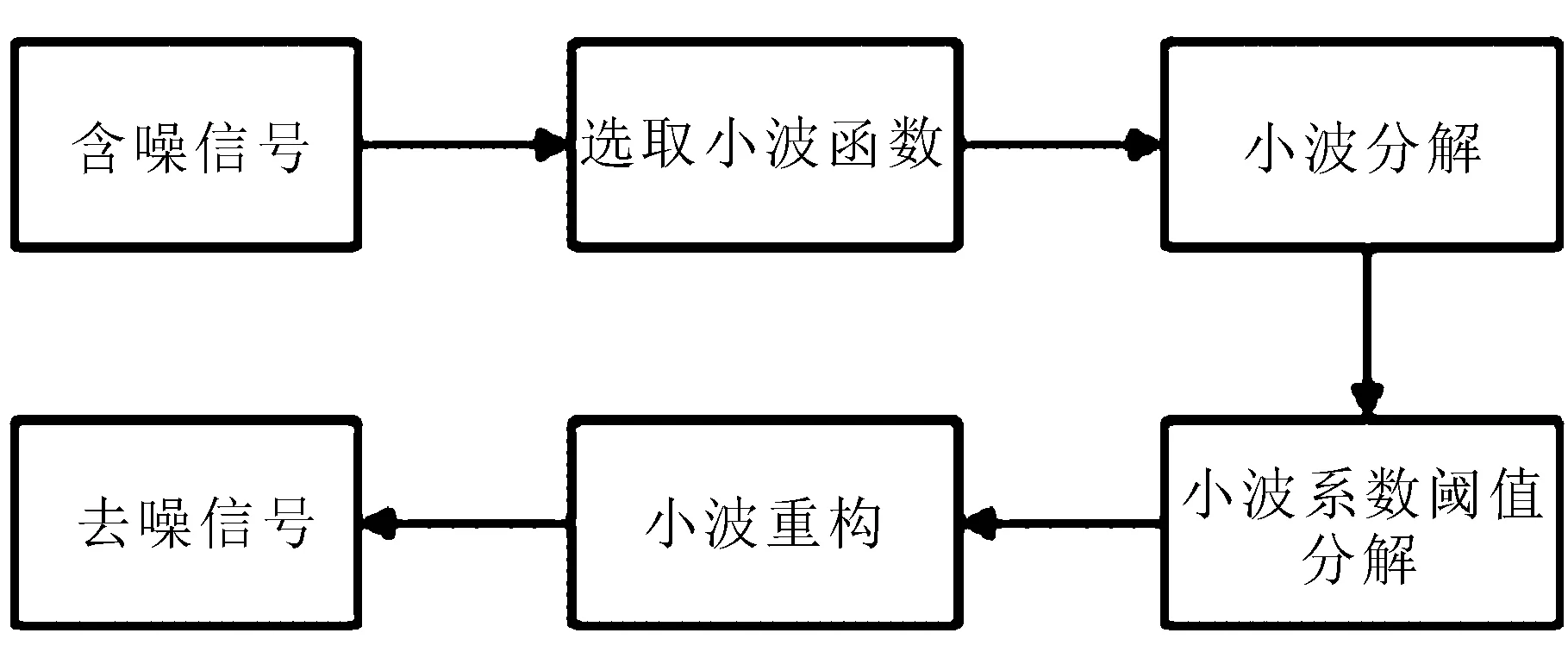
图1 小波阈值去噪算法流程

1.1 小波阈值去噪基本步骤

1)分析含噪信号特性,选择适切的小波基函数和分解层数,对含噪信号进行小波分解。文中选择小波基函数通过提前设定好分解层数和固定阈值,分别采用dbN小波、symN小波、coifN小波这几种适应度较好的小波基对含噪的行波信号降噪,将峰值信噪比作为小波基函数性能优劣的评判标准,相关结果如图2所示。

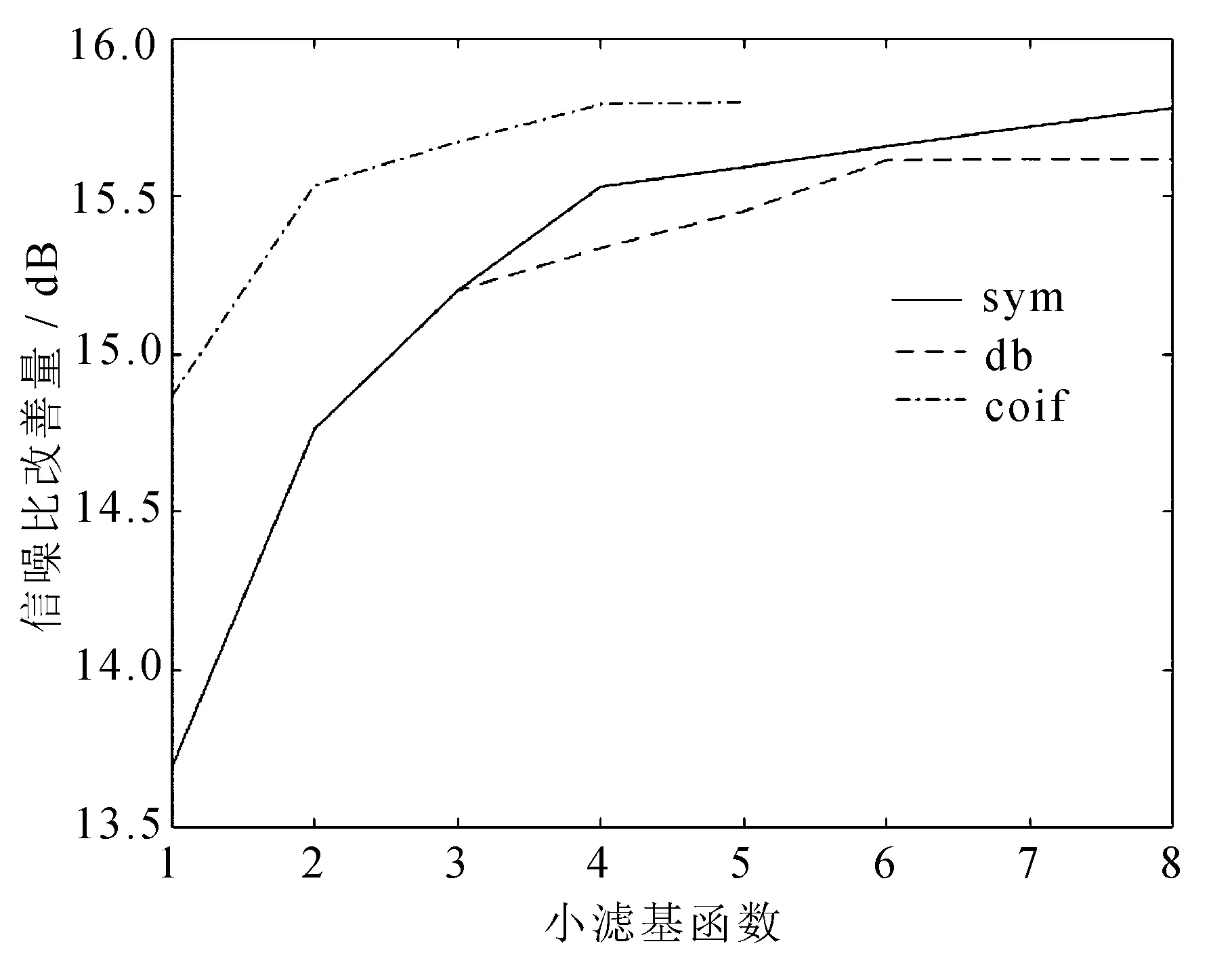
图2 不同小波函数信噪比改善量

对较为复杂的信号,分解层数一般选取3～5层。

2)借助适切的阈值函数以及阈值参数,对分解后的小波系数进行阈值处理。阈值的选取对去噪效果也会产生影响,选取阈值过大,会造成重构信号一部分有用信息缺失;阈值过小,则会保留过多噪声分量。

3)小波重组。将经过阈值处理的小波系数采取离散小波逆变换处理手段进行重组,即去噪后的信号。

进行小波变换时,不同小波基函数的滤波原理是不相同的,因此,最终还原后的信号也有较大差别。对不同信号进行处理时,选择不同的小波基,降噪的处理效果也不一样[10]。同样对信号进行多次分解,就需要庞大的运算量和极其繁杂的运算,直接影响运算效率。在达到信号的最佳分解层数之前,信噪比和分解层数之间的关系表示为近似的正相关性,达到最佳的分解层数后,信号的信噪比将不会再增大,相反还会出现减小的情况。

原始信号和干扰信号之间性质差别分明,两种信号之间的区分度会凭借分解层数的变化而表现出来。但是分解层数过多,且对所有各层小波空间的小波系数进行阈值处理,除增加无需的计算量外,也会使想要提取保留的信号信息严重丢失,直接影响后面的信号重组,造成信号失真[11]。

1.2 阈值函数

传统的阈值处理方法有硬阈值法和软阈值法。

软阈值函数

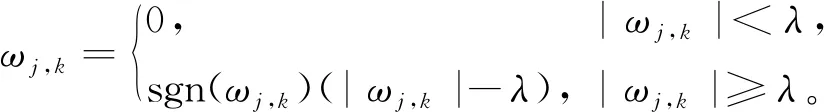
(1)

硬阈值函数

(2)

式中:ωj,k----波形分解后的第k级第j个系数;

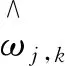
阈值公式的选取要具有普适性,一般选取

式中:N----信号点数。

其中,噪声标准方差

图形分别如图3和图4所示。

图3 硬阈值函数

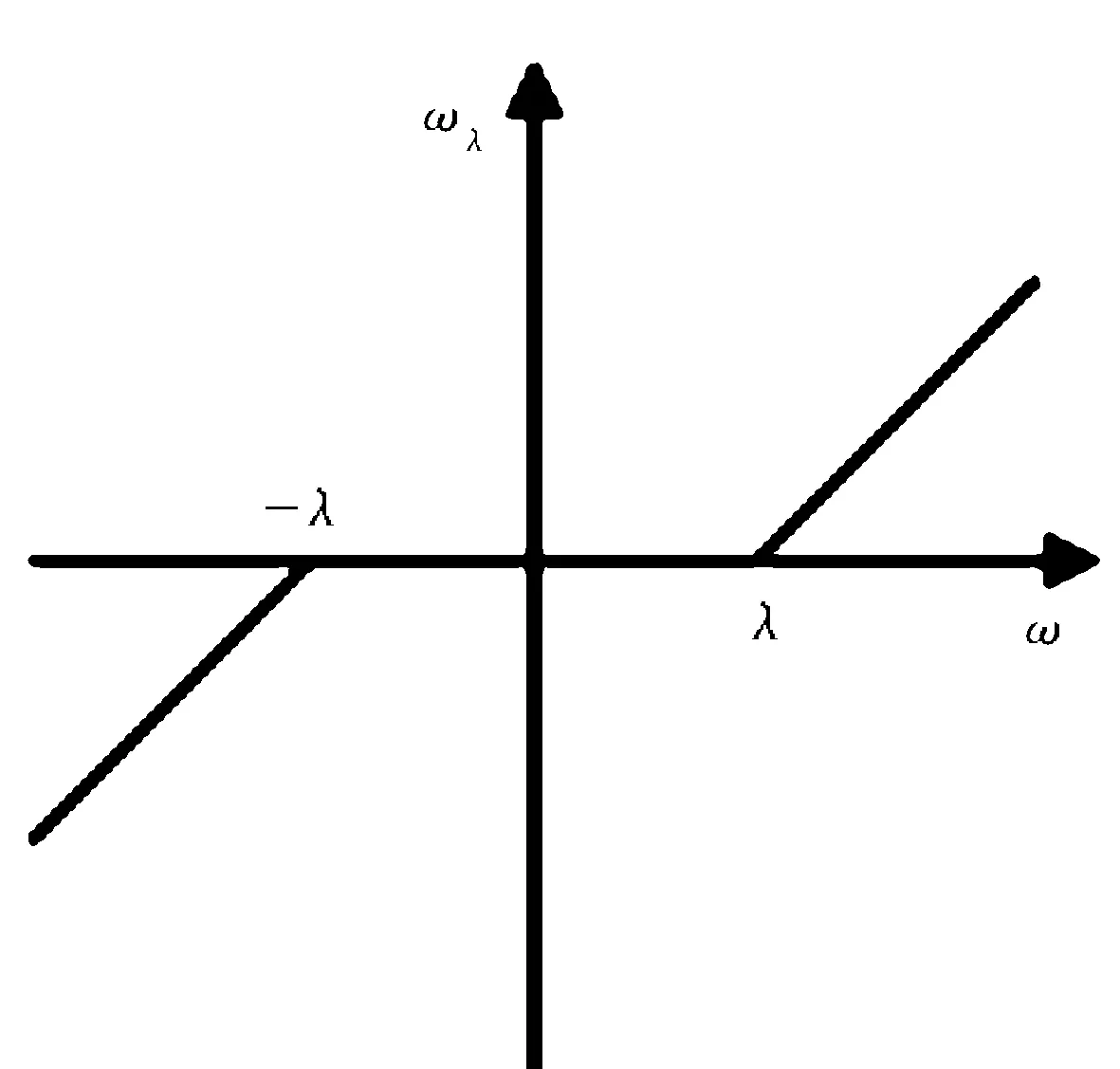
图4 软阈值函数

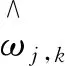
硬阈值函数含义是将比设立的判定门限小的小波系数滤除,其余的作为有效信息保留。从硬阈值函数的表达式及图示能够较为直观地看出,硬阈值函数在ω=λ处是间断的,这可能导致信号重构后产生不必要的波形震荡,产生伪吉布斯现象[13]。

硬阈值和软阈值函数特性比较见表1。

表1 硬阈值和软阈值函数特性比较

2 改进的阈值去噪方法

前面阐述了软、硬阈值函数各自特点,解决实际问题时或多或少不能达到理想状态,介于硬阈值去噪的均方误差通常较软阈值小,相比之下去噪效果较为优异,但信号重构时易发生波动。文中在保留硬阈值函数优点的同时,凭借其提出一种改进的阈值去噪方法,其阈值函数为

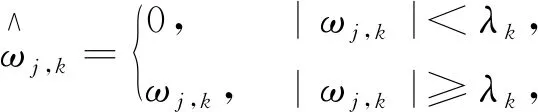
(3)

其中,

为新设定的阈值,其代表小波分解后第k层的阈值。新阈值函数具有下列优势:

1)对干扰信号较集中的低层空间的小波系数在阈值处理上设立较大的门限,对高层空间的系数则设立较小的门限。这是由干扰信号能量在小波变换各尺度上的散布规律所决定的。能够保证过滤低层干扰信号的同时保留高层有用信息。

3)与硬阈值函数相比,逐层递减的阈值减小了小波系数的跳变幅度,从而很好地改善了重组信号的平滑性。

3 仿真实验

利用PSCAD仿真软件搭建电力电缆局部放电传播的仿真模型,通过控制断路器的开断来控制脉冲信号的宽度,通过改变局部放电脉冲信号发生器与信号检测传感器之间电缆长度来模拟局部放电信号在不同长度电力电缆中的传输,然后对比分析检测到的电压波形变化规律[14]。电缆结构模型以及局部放电结果分别如图5～图7所示。

图5 电缆结构图

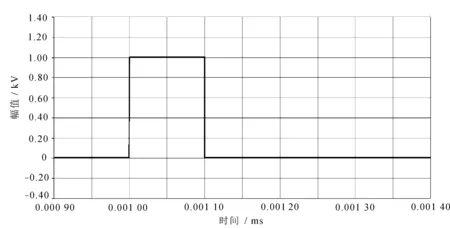
图6 触发脉冲信号

图7 局部放电信号

为了验证文中所提新阈值函数的有效性,借助Matlab 2016软件进行信号去噪仿真实验。选取高斯白噪声作为干扰信号,将其引入原始信号中进行实验。

仿真试验后有关去噪效果的界定一是可以通过图像对比,二是引入两个参数通过其数据量的改善进行判定。分别是信噪比(SNR)、均方误差(MSE)。其中SNR和MSE函数表达式为:

(4)

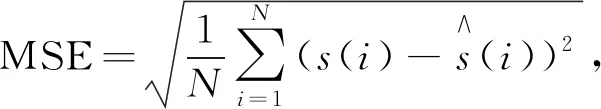
(5)

式中:s(i)----原始信号;

信噪比反映了有用信号和无用信号所含能量的比值。降噪后的信噪比同加噪信号比,其数值越高,说明要提取的信号占比越高,信号还原度越高;均方误差则反映了降噪信号与原始信号的偏离程度,其值越小,表明信号失真程度越小[15]。文中在小波阈值去噪算法仿真中选取小波基函数sym8小波,分解层数选择5层。

在原始信号中加入SNR=0.005的高斯白噪声,实验结果分别如图8～图13所示。

图8 不含高斯噪声的局部放电图

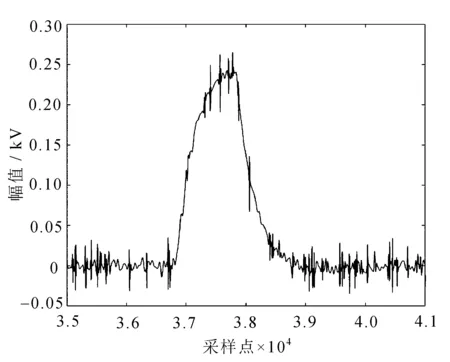
图10 硬阈值去噪

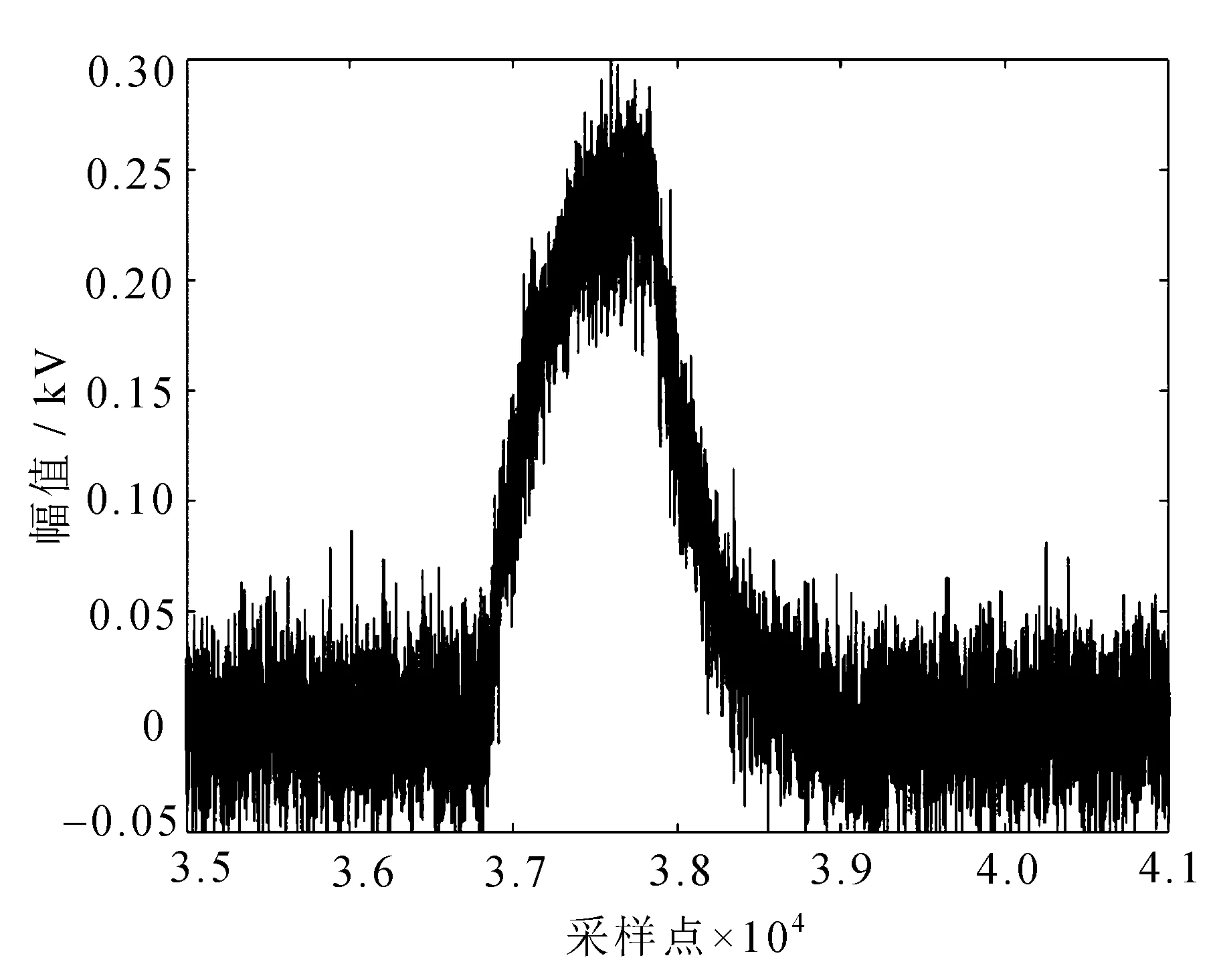
图11 软阈值去噪

图12 改进的阈值函数去噪

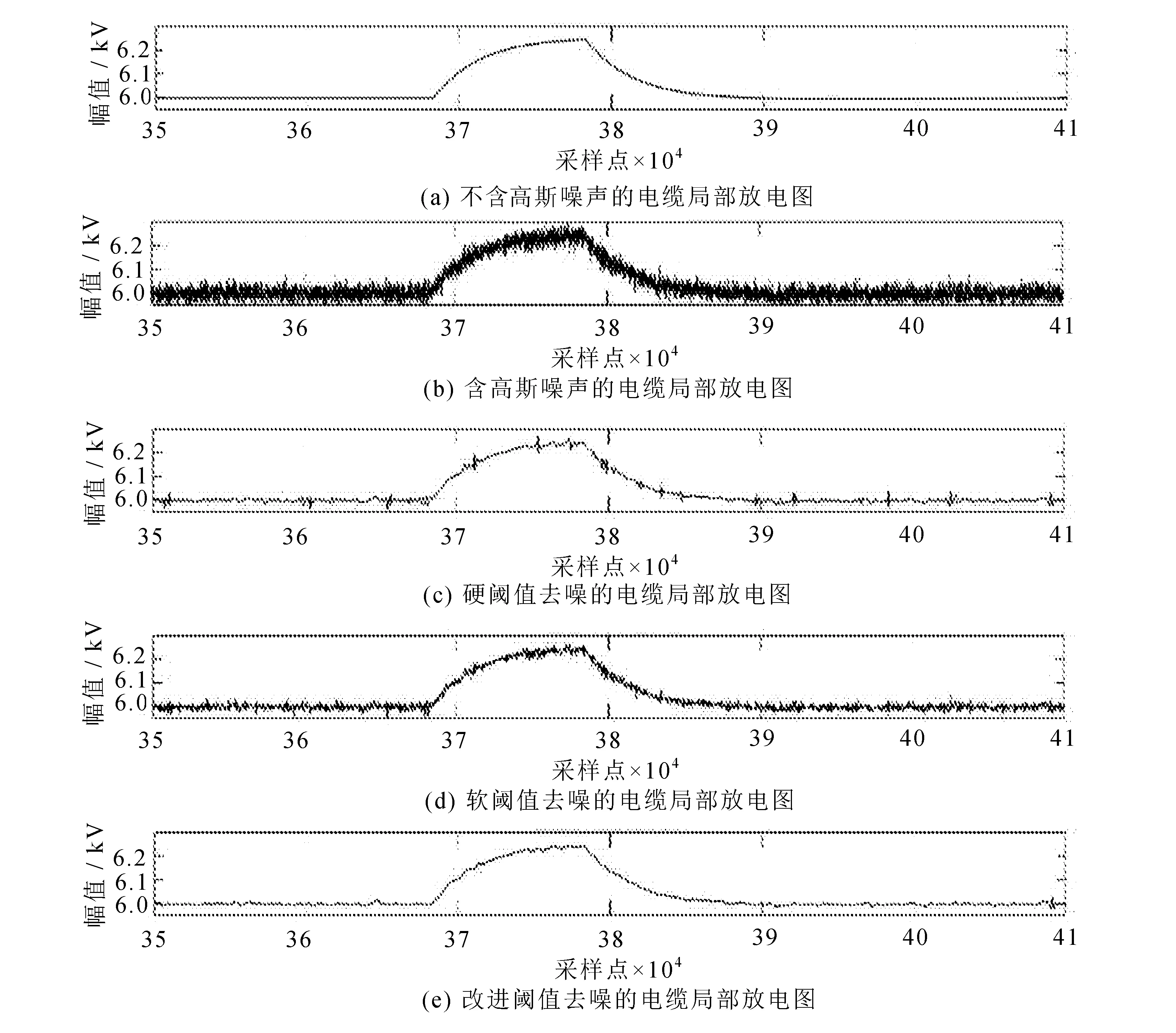
图13 去噪效果对比

加入SNR=0.005 0的高斯白噪声局部放电信号的三种去噪结果定量比较见表2。

表2 加入SNR=0.005 0的高斯白噪声局部放电信号的三种去噪结果定量比较

在原始信号中加入SNR=0.002 5的高斯白噪声,实验结果分别如图14～图19所示。

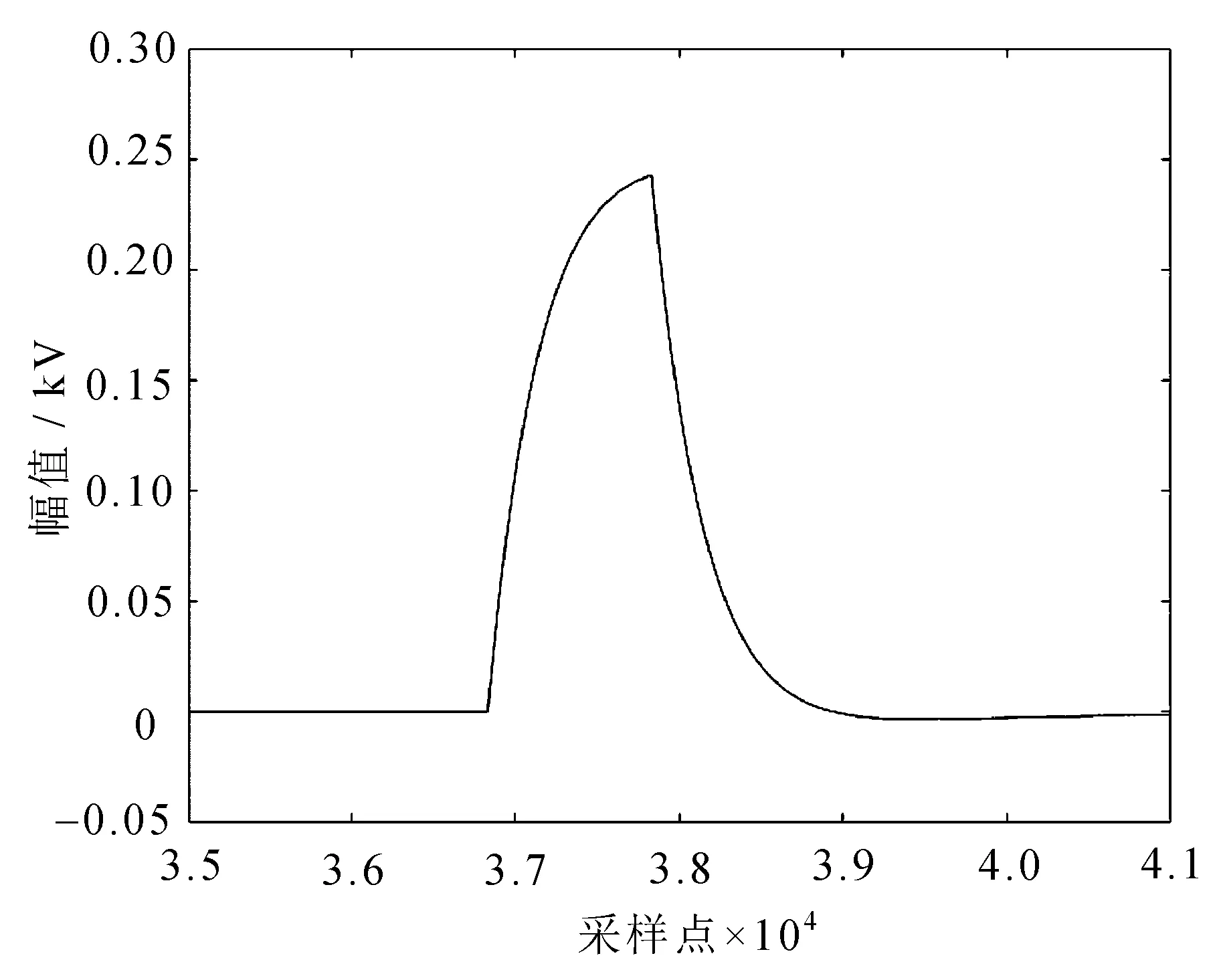
图14 不含高斯噪声的局部放电图

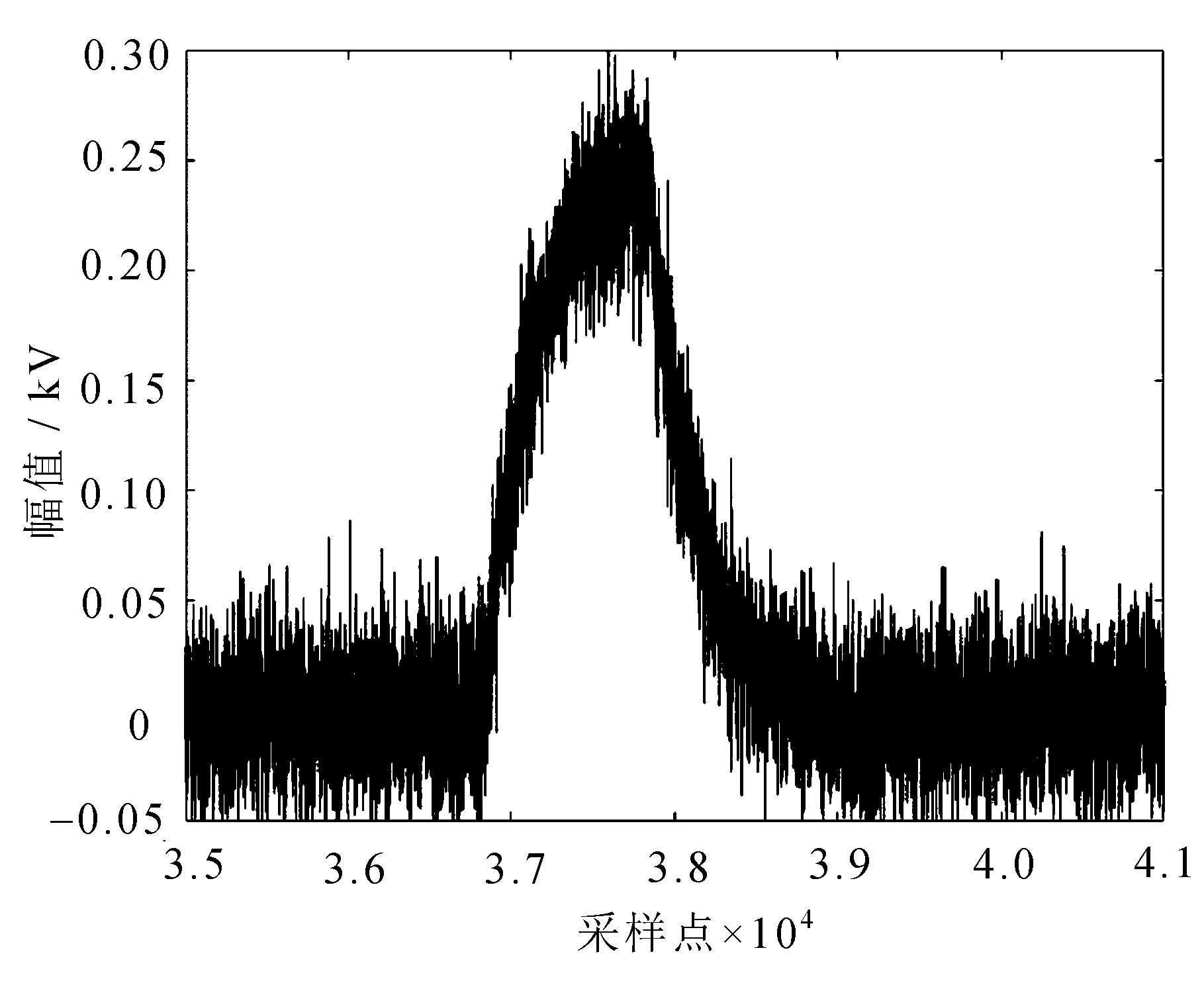
图15 含高斯噪声的局部放电图

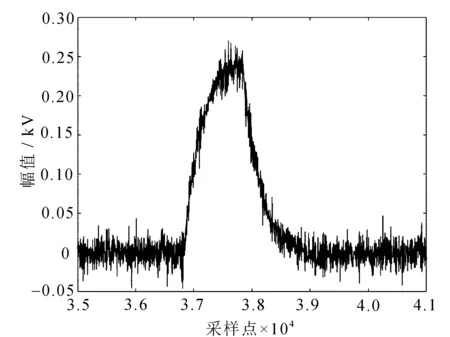
图16 硬阈值去噪

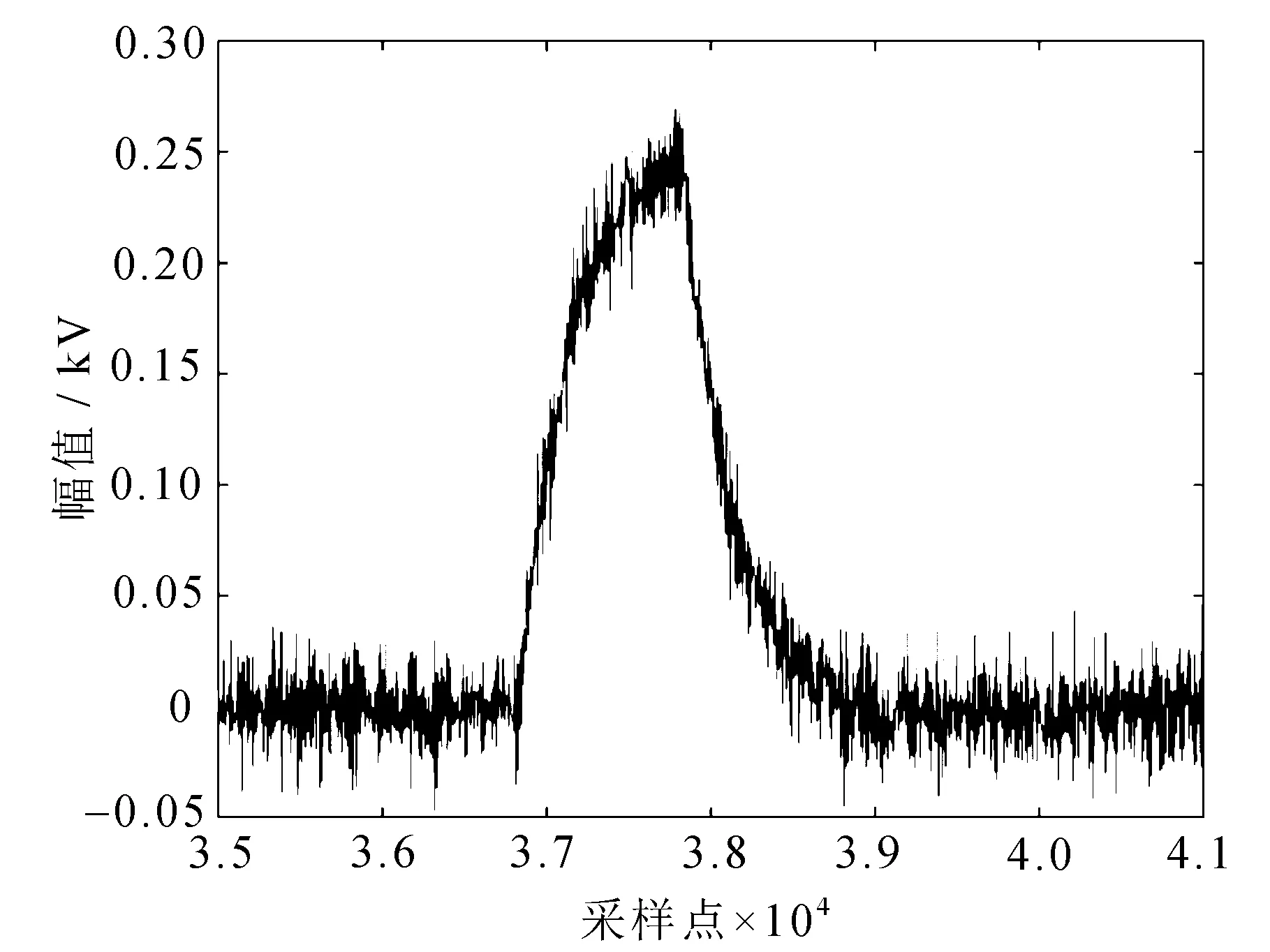
图17 软阈值去噪

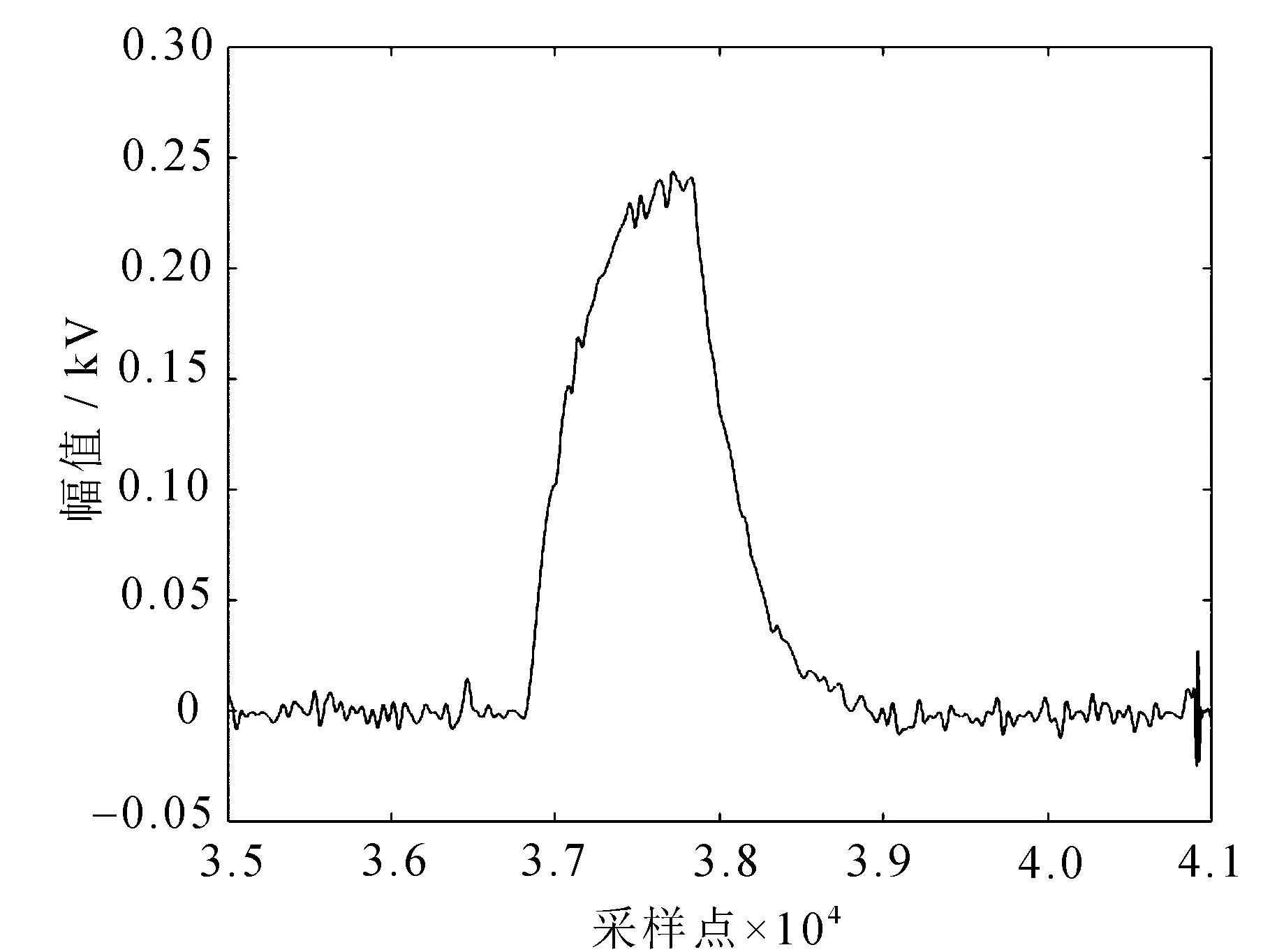
图18 改进的阈值函数去噪

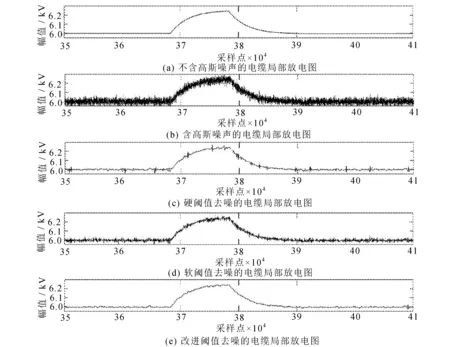
图19 去噪效果对比

加入SNR=0.002 5的高斯白噪声局部放电信号的三种去噪结果定量比较见表3。

通过向原始信号分别加入信噪比为0.005 0和0.002 5的高斯白噪声,对其进行软、硬阈值以及改进的小波阈值降噪实验,从实验结果可以清晰看出,改进的阈值函数在降噪处理上与传统的硬阈值函数和软阈值函数比有一定提升。从两次实验结果得到的信噪比和均方根误差表分析可以得出,新阈值函数相对于其他阈值函数具有更高的信噪比,且均方根误差最小,从数据上表明,新阈值函数具有更好的去噪效果。

4 结 语

基于小波阈值去噪的基本原理,从阈值函数的角度来研究去噪效果,通过建立电缆局部放电模型,引入高斯白噪声作为局部放电信号的干扰源,分别利用传统的硬阈值去噪和软阈值去噪法对其进行降噪处理。针对传统阈值函数在降噪过程中存在的缺陷,提出一种新的阈值函数,改善了传统阈值函数在阈值处不连续以及重构信号与原信号存在恒定偏差的问题。实验结果可以看出,利用改进的小波阈值函数去噪后的波形相似度更高,对噪声的抑制能力更强,达到了比较理想的效果。