融合Stacking集成算法的联邦学习技术

岳靖轩, 陈志雨, 刘 钢

(长春工业大学 计算机科学与工程学院, 吉林 长春 130102)

0 引 言

当前,个性化金融服务是金融机构保持市场竞争力的重要方向,金融机构根据企业或个人以往的交易记录、社会信用等信息完成建模画像,实现违约风险识别、银行贷款个性化定价[1]等业务,结合内部资金转移定价(FTP)模式优化配置资源、合理引导定价,逐渐形成为不同客户提供科学评价和定制化的金融服务。

中小型银行业务范畴相对单一,采集到的本地数据量维度稀疏。生产中为了解决这一问题,不同行业将数据上传至公共数据平台,根据用户的身份信息将数据对齐。该方法虽能解决数据稀疏和特征空间不足的问题,却未能保障数据的隐私与安全性。联邦学习的出现,有利于打破数据孤岛,实现企业之间联合建模,通过更高维度的数据和更多的样本来提高模型的建模能力。王健宗等[2]提出让参与方将数据存储在本地不进行传输,只交换模型参数,有效防止了第三方或参与方恶意窃取敏感数据,联邦学习模型训练流程如图1所示。

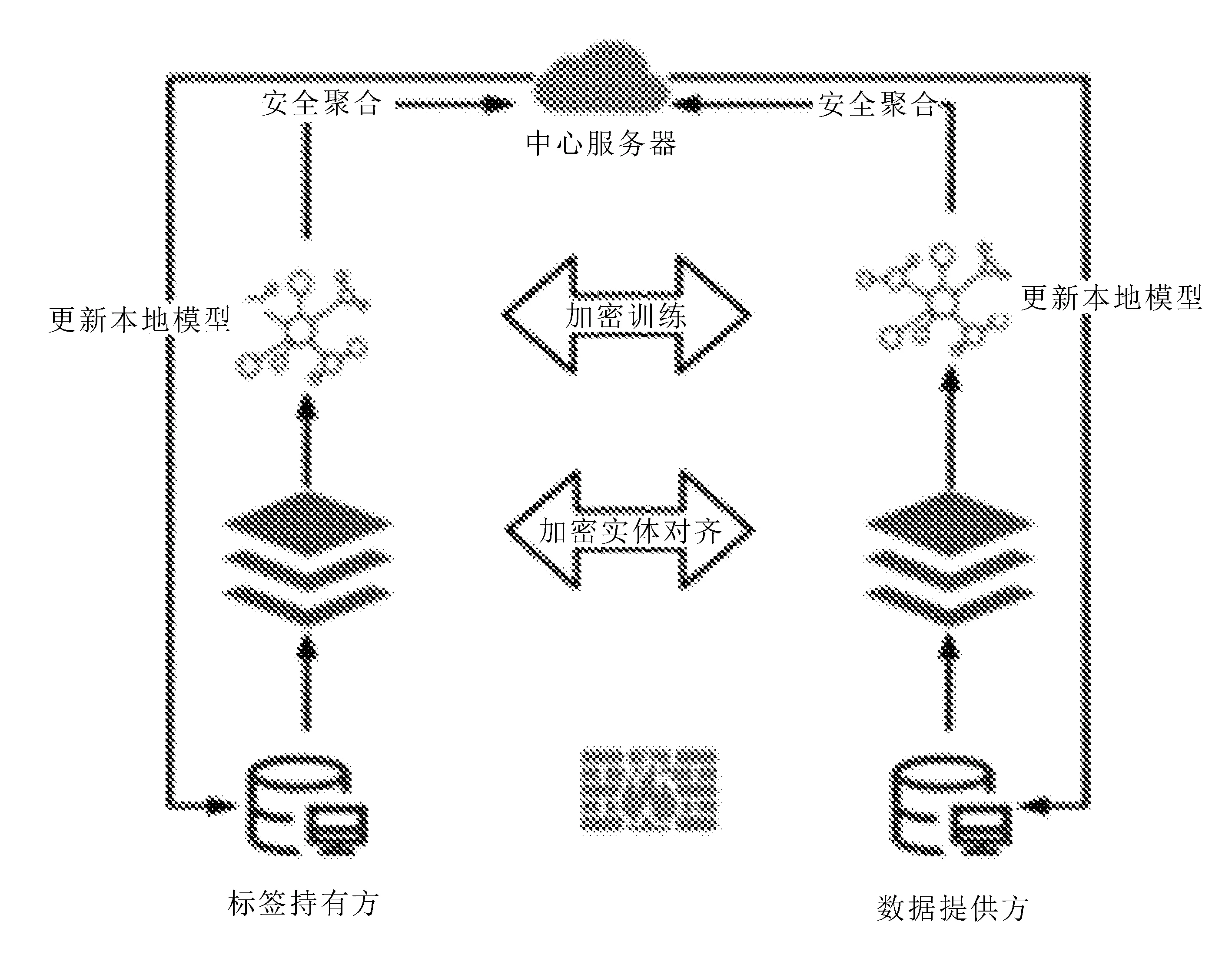
图1 联邦学习模型训练流程

邓涵宇[3]提出通过联邦学习联合多个参与方建模,解决了小微型信贷行业数据维度稀疏、数据来源少、覆盖范围不足的问题。

已有的联邦学习大多采用单个算法进行联合建模,容易引发过拟合,影响模型的鲁棒性。文献[4-5]表明,集成学习在预测性能和泛化能力上优于单个模型算法。受此启发,张艳艳[6]提出通过集成学习来构建个性化贷款业务的定价模型,将集成方法融入联邦学习中,模型通过多个“好而不同”的联邦学习基学习器共同训练参与方本地数据,提高联邦学习算法的泛化能力,能更有效地处理异常数据。实验结果表明,Stacked-FL集成算法对中小型企业数据维度稀疏、安全性差、模型泛化能力差的问题起到了显著的缓解作用[7]。

综上所述,文中将联邦学习与集成方法相结合。

1)提出了融合集成学习模式的联邦学习框架,显著提高了小维度数据建模的安全性与模型预测的准确性。

2)增强了联邦模型的泛化能力,对异常值的处理更具鲁棒性。

1 相关研究

贷款定价的方法主要有两种:专家评估法和模型评分法,前者需要耗费大量的人力且评估尺度难以统一;后者更为高效和公平,因此更符合小型银行的需求[8-9]。刘昊辰[10]提出一种基于XGBoost的农村中小金融机构贷款利率定价研究,证明了XGBoost对中小型数据集在定价准确性上,要优于其他机器学习算法及专家评估法。该方法通过建立重视客户的数据库,扩充了实验的样本数量和样本维度,有效解决了中小金融机构由于数据维度低及样本稀少的困扰,但在建立公共数据库的过程中容易暴露用户的隐私,参与方和第三方数据库可以窃取用户的隐私数据,在数据传输过程中也有被窃取的可能[11],无法保障用户隐私的安全。

为了提高贷款定价模型的性能,Li M X等[12]将集成模型和卷积神经网络(CNN)相结合,提出了Stacking CNN的贷款预测模型。集成算法先训练多个算法作为基学习器,并对数据进行切分处理,Stacking集成学习流程如图2所示。

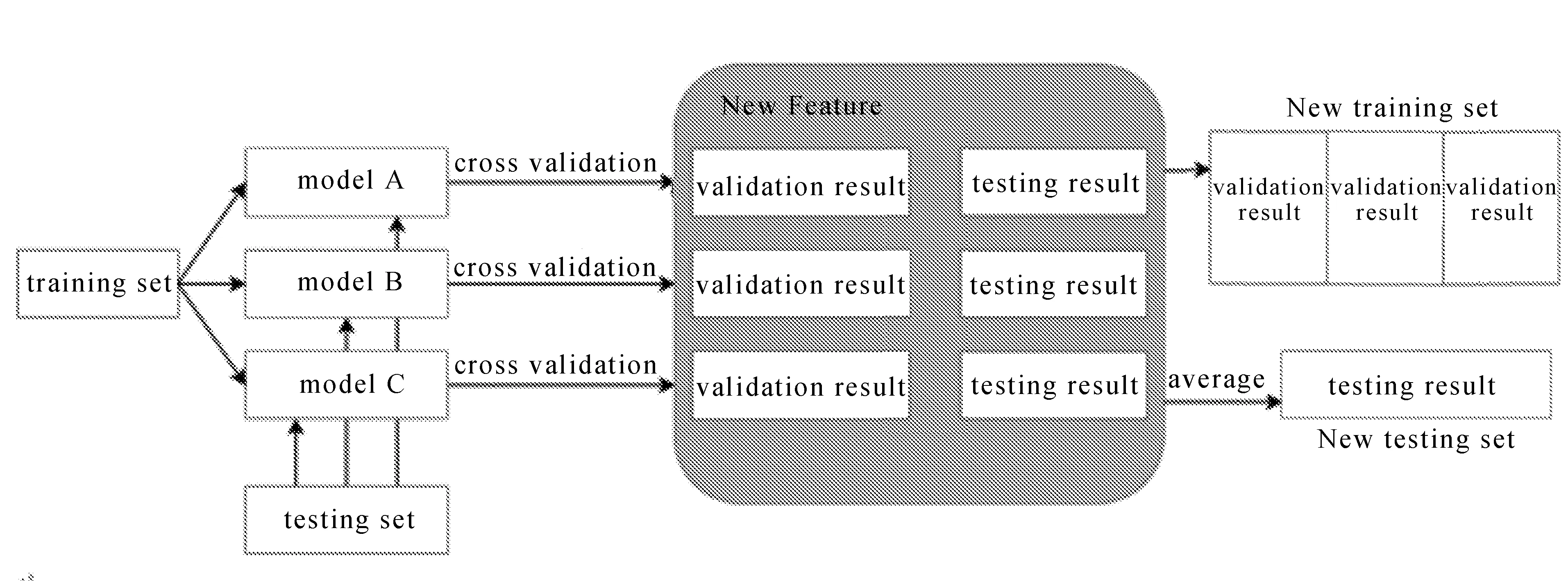
图2 Stacking集成学习流程

将训练结果作为特征输入到元学习器中训练,得到最终结果。该模型发挥了Stacking集成方法的泛化能力,提高了模型预测的准确性,证明Stacking集成方法适用于贷款定价模型,且效果要优于传统的单个模型[13]。

采用集成学习的优势在于:

1)从统计学角度来说,算法结合多个学习器,提高了模型的泛化性能;

2)从计算角度来说,降低了陷入局部极小值的可能性;

3)从表示的角度来看,扩大了假设空间,可能得到更近似真实值的预测结果。但是仍然受限于数据集维度及样本数量,对于维度稀疏的数据集无法精准预测。

Cheng K W等[14]提出一种新的基于联邦学习的无损隐私保护树增强系统(SecureBoost),该算法将梯度树增强算法无损地应用到联邦学习中。为了防止标签信息被参与方窃取,还提出了更安全的完全SecureBoost,构建的第一棵子树由任务发起方构造,数据提供方只能拿到第一棵树的训练结果。张君如等[15]提出一种基于联邦学习的安全树(FLSectree)算法预测用户行为,通过更新实例空间寻找最佳的分裂点,收敛后更新参数,在保障隐私的前提下,未降低预测的准确度,减少参与方通信的次数,节约了预测时间和通信资源。

综上所述,传统机器学习解决中小型银行个性化贷款定价的缺点在于安全性不能得到保障。为了提升安全性和准确性,文中将联邦学习与集成算法相结合,用于中小型银行贷款定价。SecureBoost作为集成算法中的基学习器,相比SecureBoost,同样在保证数据安全的前提下,预测效果和泛化能力进一步提升。

2 模型设计

2.1 模型描述

为了保证用户的隐私安全,实现多个参与方使用本地小维度数据集训练模型,并做出精准的预测。文中构建了纵向联邦学习集成模型,其中基学习器选择线性回归(Linear)、泊松回归(Poisson)和SecureBoost。实验包含数据预处理模块、加密实体对齐模块、联邦算法模块、集成模块。

1)首先标签持有方发起联邦学习任务,参与方分别对本地数据进行预处理后,再用RSA加密算法对每个参与方本地数据进行加密,并完成加密实体对齐。

2)由中央服务器向数据持有方及数据提供方发送基学习器初始化参数{mA1,mA2,…,mAn}、{mB1,mB2,…,mBn},n为基学习器的数量。对基学习器参数进行更新后,模型根据本地数据集进行K折交叉验证,两个参与方将梯度K组[{gA1,gA2,…,gAn},{gB1,gB2,…,gBn}]加密后发送到中心服务器,经过聚合完成一次迭代,迭代多次后拟合得到最优全局模型。该方法相比单个联邦学习算法参与方之间参数交互如图3所示。

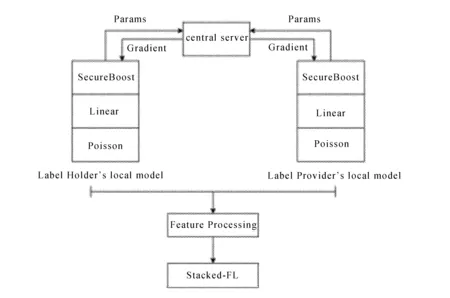
图3 Stacked-FL参与方交互流程

3)标签持有方更新了多个基学习器训练的全局模型。将模型预测结果整合成元学习器的训练集和测试集的特征,组合成两个新的数据集。

4)Stacking集成学习的元学习器的选择为较简单的模型,实验中选择线性回归作为实验的元学习器。对元学习器参数进行更新后,使用新的训练集进行训练,得到模型结果用测试集进行模型效果的测试,如果得到不是最优解,则调整元学习器参数,重新训练并测试模型效果,直至效果最优。最后采用Voting、Average方法对各参与方的数据进行集成,与Stacking方法进行对比分析。

2.2 模块分析

2.2.1 数据预处理模块

数据预处理是构建模型十分重要的环节,根据应用场景的不同,各参与方数据的结构差异以及数据存储方式不同的一系列因素的影响,在本实验中,为了解决数据样本维度稀疏以及学习器不容易对属性数据处理的问题,采用独热编码(One-Hot Encoding),可以从一定程度上起到扩充特征的作用。为了避免个别特征数值过大对实验结果造成预测结果的偏差,文中采用数据的归一化(Normalization)让数值较大的数据限定在一定的范围内,在梯度下降的时候,会使模型的方向发生偏离。

2.2.2 加密实体对齐模块

由于参与方之间用户样本差异性较大,首先要找到重叠的样本,一般通过身份证号、手机号码等敏感信息找到多个参与方的重叠用户。在联邦学习计算过程中,为了使参与方交换中间计算结果时参与方重叠的样本不被恶意方推测用户的信息。本实验使用一种基于RSA对ID进行对齐的方法使模型间无须通过中心化的方式采集共同数据,仅采用点对点密文的方式传递数据信息,即可实现去中心化,确保每个参与方的数据不向其他参与方暴露的情况下,对用户ID进行加密,并将所有参与方中重叠的用户ID对齐,实现维度的补充。

2.2.3 联邦算法模块

2.2.3.1 SecureBoost

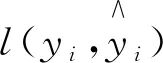
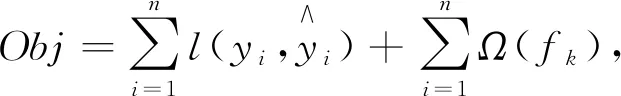
(1)

式中:yi----标签的真实值;

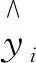
每当模型增加一棵树,损失函数就会在原有的基础上加上新的回归树fT(xi),在更新第T轮时,目标函数为

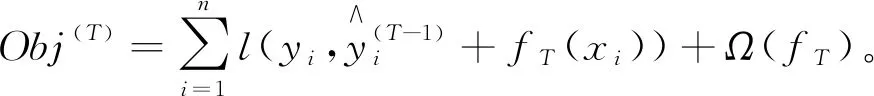
(2)

最后计算出损失函数用l表示,并对其求一阶导数gi,二阶导数hi:

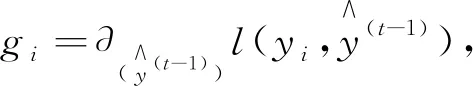
(3)

(4)

为了确定数的每一层的最佳分割,就要从分割带来的增益来衡量,它可以通过之前求出的gi和hi计算得出。

2.2.3.2 线性回归

纵向联邦学习线性回归[16]使用梯度下降方法去训练模型,为了保证得到模型的损失和梯度,且保证在训练过程中的安全,其损失数函数为

(5)

式中:yi----发起方的标签空间;

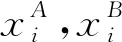
θA,θB----模型参数,经过同态加密[18]后的加密损失为

(6)

训练参数的损失函数的加密梯度gA,gB可以表示为

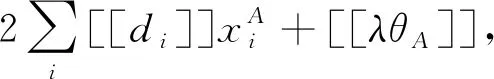
(7)

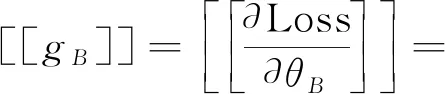
(8)

计算梯度后,对梯度分别加上加密的随机掩码[[RA]]、[[RB]],得到[[gA]]+[[RA]]和[[gB]]+[[RB]]发送至中心服务器完成聚合,根据聚合后返回的参数更新本地模型。

2.2.3.3 泊松回归

泊松回归通常用于描述单位样本空间内的小概率事件,自变量银行利率服从泊松分布,在实验中使用exposure变量接收数据,其列名可以在配置参数中指定,在配置中指定暴露元素。纵向联邦学习泊松回归在计算流程上与线性回归相似,由参与方、发起方分别计算出损失函数

L=([[exp{WAXA}]]*exp(WBXB-Y),

(9)

式中:WA,WB----参与方本地泊松回归参数;

XA,XB----解释变量。

计算出损失L后,将加密后的损失[[L]]传递给参与方后,分别计算梯度[[gA]],[[gB]]。

2.2.4 集成算法模块

集成学习(Ensemble Learning)通过用某种结合策略将多个基学习器进行融合,共同训练一个模型。通过集成SecureBoost、Linear回归、Poisson回归三个模型,集成后的模型往往可以获得比基学习器更好的性能,以及更强的泛化能力[17]。文中采用集成学习有Stacking、Voting、平均法等。

算法1:Stacked-FL

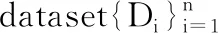
输出:local model and global model

for epoch=0 to N //N is the number of base learners

2. for i =0 n //general secret key

3. Pi=RSA(x); pi=RSA(x)

4. end for

5. for i=0 to n //local model train

6. for j=0 to n

7. yj=mj(Di)

8. end for

9. end for

10. yi=concat[y0+y1+...+yk-1]

11. for i=0 to n //Integration model

12. Si=Pi(Yi)

13. Ci=pi(Si)

17. end for

18.end for

19. //update local model

2.3 算法可行性分析

提出的Stacked-FL集成方法实现了集成方法与联邦学习相结合,适用于不同领域或者同领域、特征重叠少的参与方的小维度数据集联合建模,提高了传统集成模型的安全性,也提高了联邦学习的准确性与泛化能力。该方法的优势在于避免了传统的机器学习模型要在流通的数据上进行融合存在隐私泄露的风险,并且通过多个基学习器对模型进行训练和集成,从更全面的角度对数据进行分析。

3 实验与结果分析

3.1 实验环境

使用Pycharm软件和Python3.8语言进行实验,实验环境采用三台腾讯云服务器(操作系统为CentOS7.5,4Core,内存8 G)。

3.2 数据集分析及评价指标

实验采用Lending Club的公开数据。Lending Club 创立于2006年,主营业务是为市场提供P2P贷款的平台中介服务,公司总部位于旧金山。公司在运营初期仅提供个人贷款服务,至2012年平台贷款总额达10亿美元规模。Lending Club把借款人和投资者联系起来。为了模拟中小型银行小数据集的特点,文中将使用2007-2010年的9 578条贷款数据,选取贷款利率(预测值)、贷款用途、是否分期付款、借款人年收入的自然对数等7个特征模拟银行A(任务发起方),选取借款人的循环余额、循环额度利用率、被债权人查询的次数、逾期30 d以上的次数、贬损公共记录的数量等6个特征模拟银行B(数据提供方)。实验的评估指标采用平均绝对误差(mean_absolute_error, MAE)、均方根误差(root mean squared_error, RMSE)来评估模型的准确率,

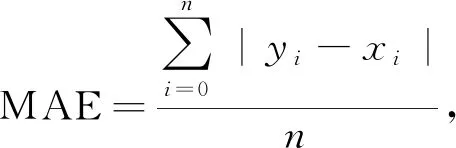
(10)

(11)

3.3 实验设置

元学习器参数设置见表1。

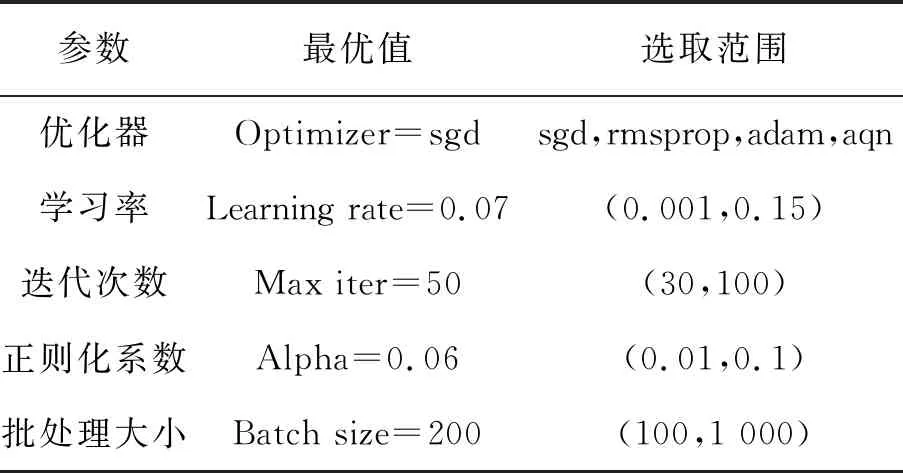
表1 元学习器参数

SGD优化器的训练速度快,支持在线更新,有概率跳出局部最优解,对于多批次的小数据集训练效果较好。实验中对批次大小(100,1 000)范围内进行测试,批次样本数选择为200的准确度最佳,且对计算效率的影响较小,实验结果分别如图4和图5所示。

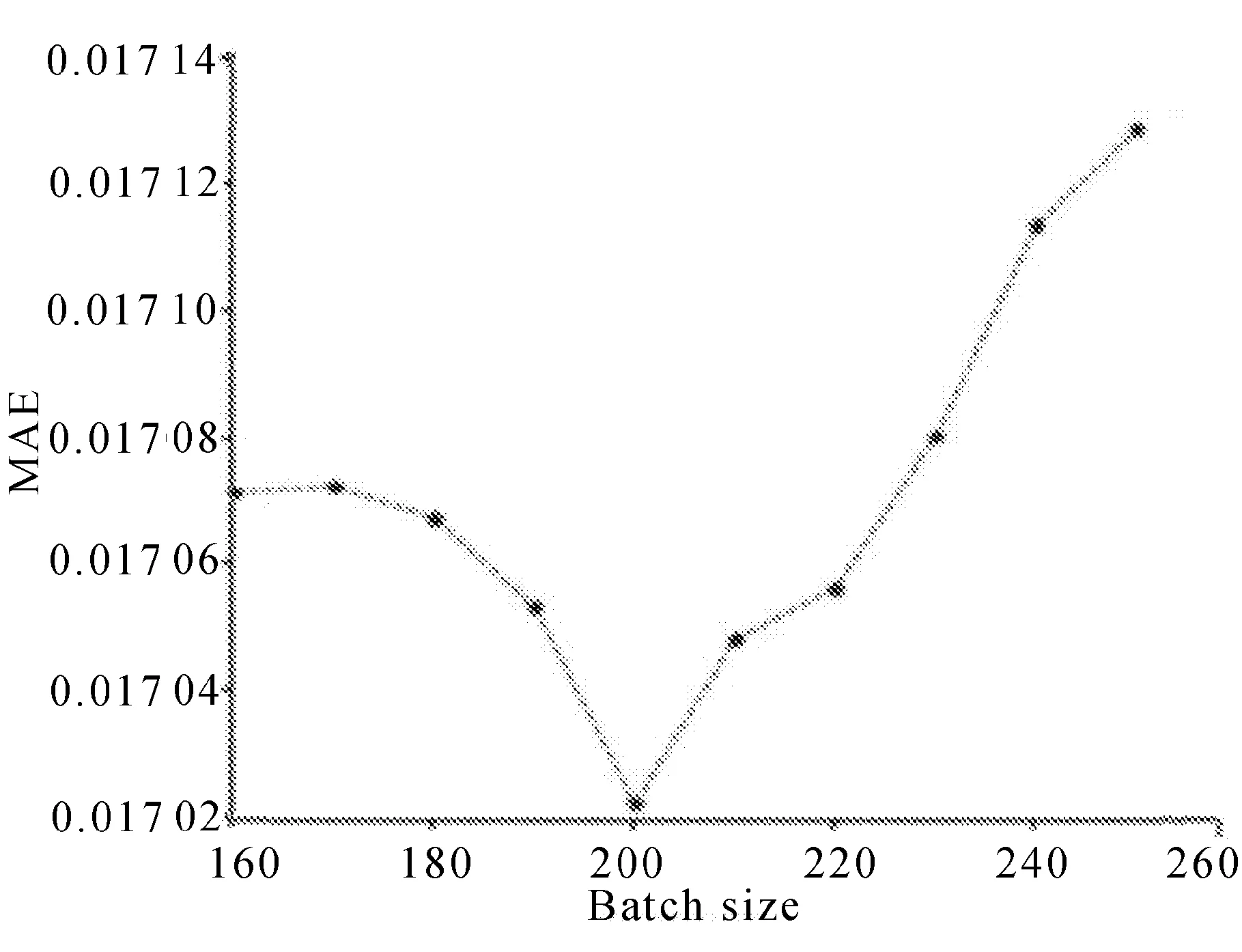
图4 批量大小对MAE值的影响

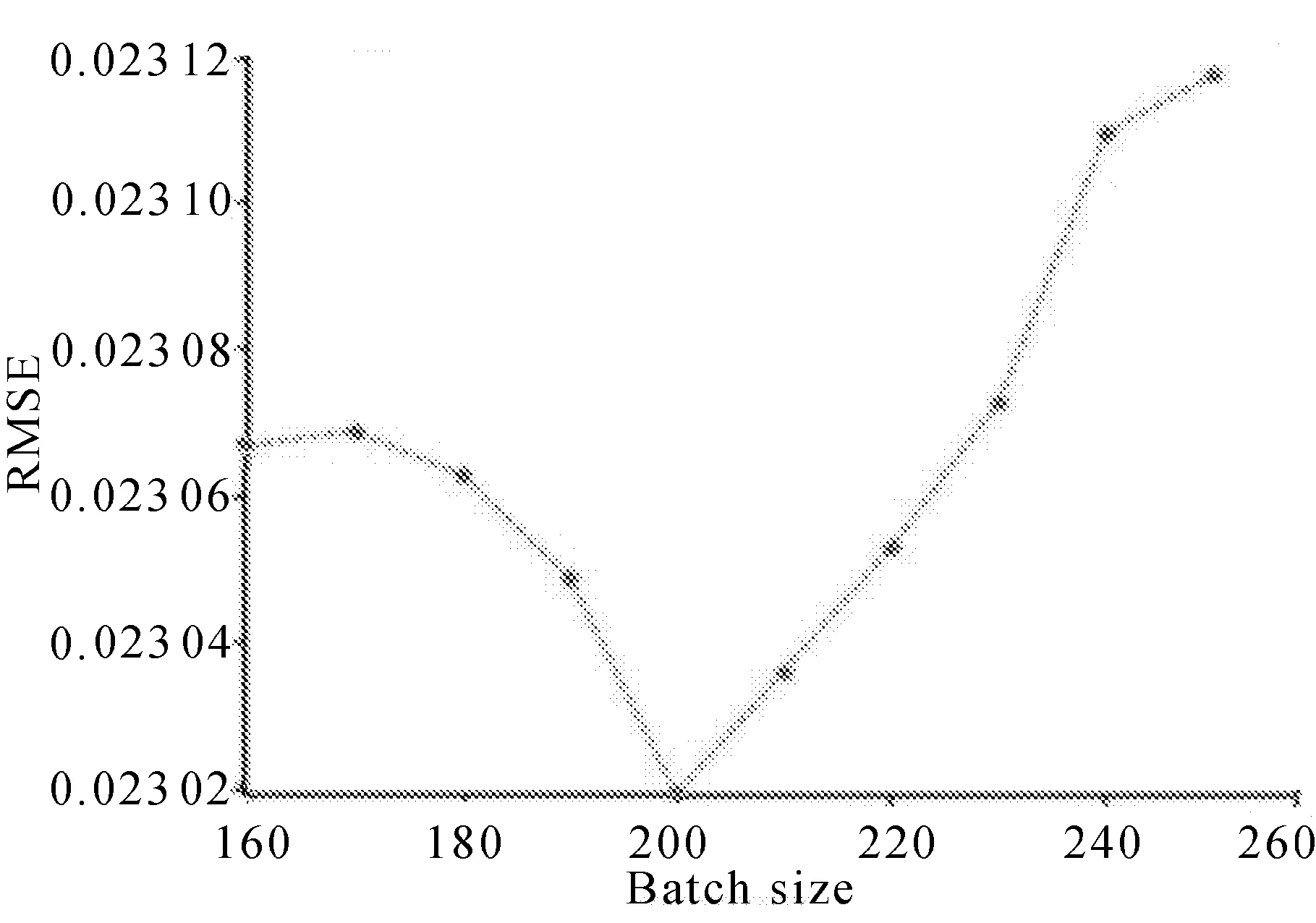
图5 批量大小对RMSE值的影响

线性回归学习率一般在0.1左右,实验中对0.001～0.150进行了测试,当学习率为0.07时,收敛速度与误差精确度表现较好, 实验结果分别如图6和图7所示。

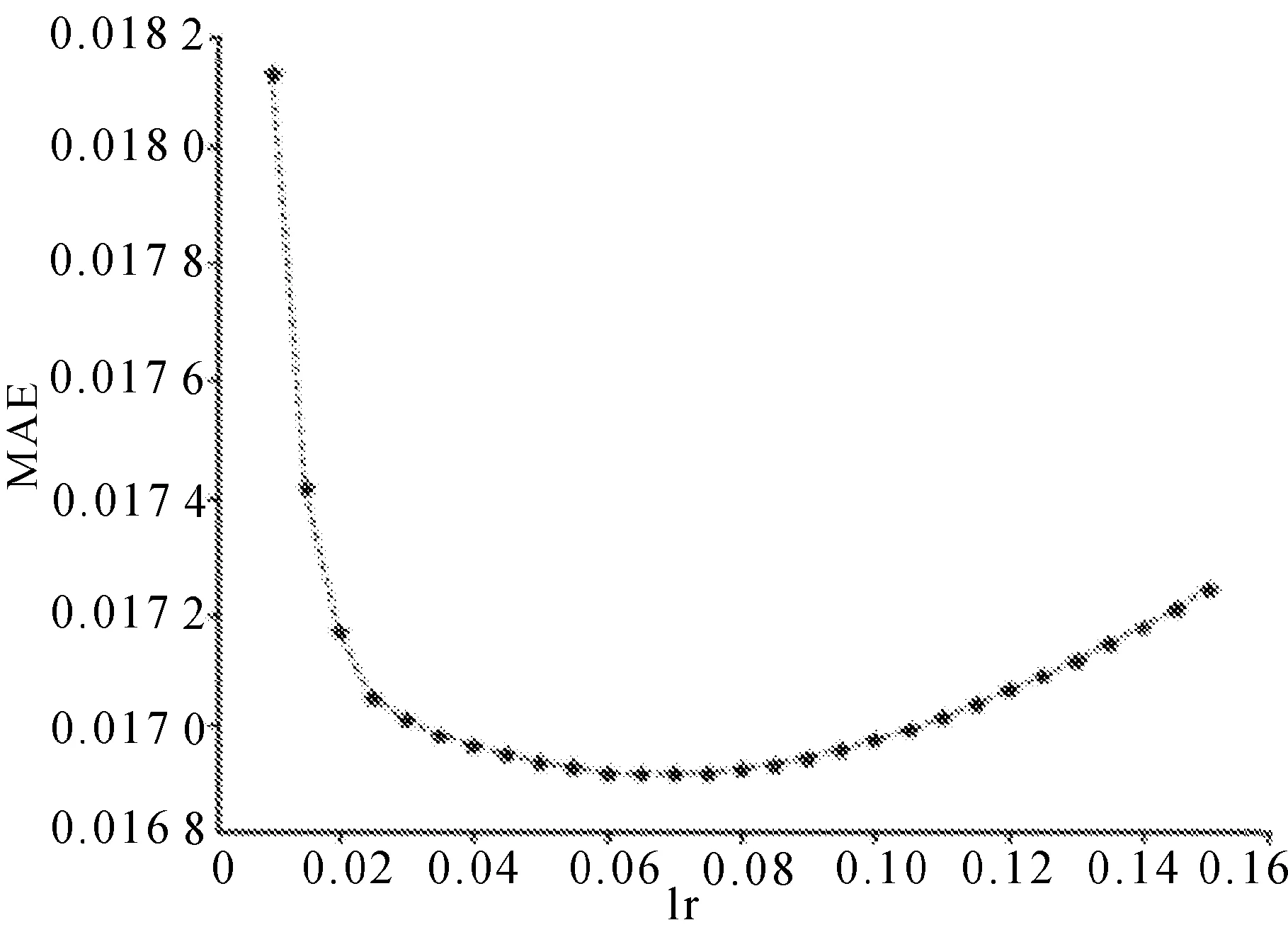
图6 学习率对MAE值的影响

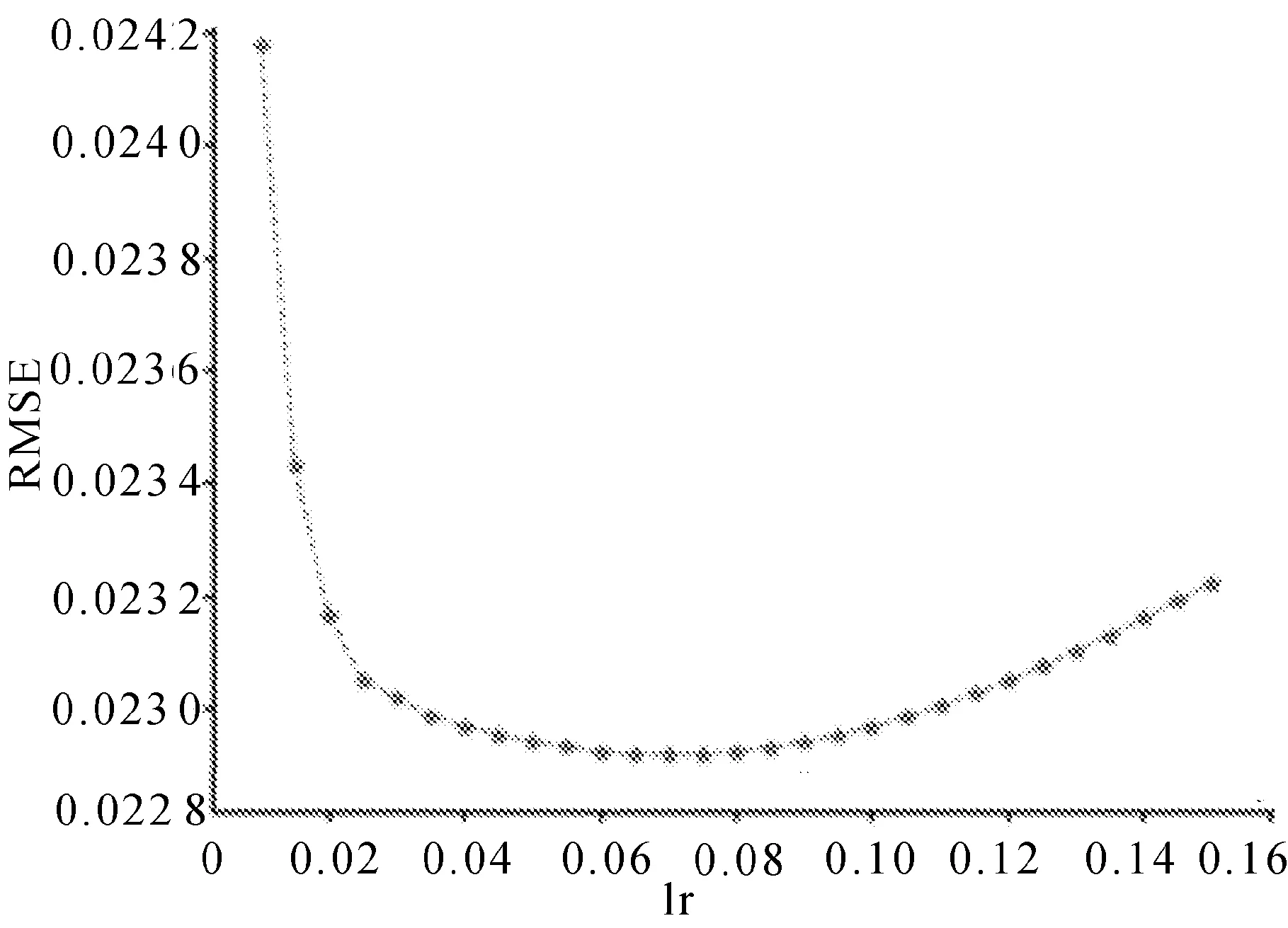
图7 学习率对RMSE值的影响

最大迭代次数选取50,原因是在迭代50轮时效果已经趋近拟合。为了提高模型效率,节约计算资源,将最大迭代次数选择50轮。由于训练集较少,为了避免过拟合,在实验中采取L2正则化,限制了模型的复杂程度,缩短了计算时间,在0～0.10效果最佳,并对(0,0.10)区间进行实验,结果显示,正则化系数设置为0.08时,MAE值效果最佳,RMSE值下降幅度较小,在保证有足够泛化能力的同时,还不会造成欠拟合的风险,实验结果分别如图8和图9所示。

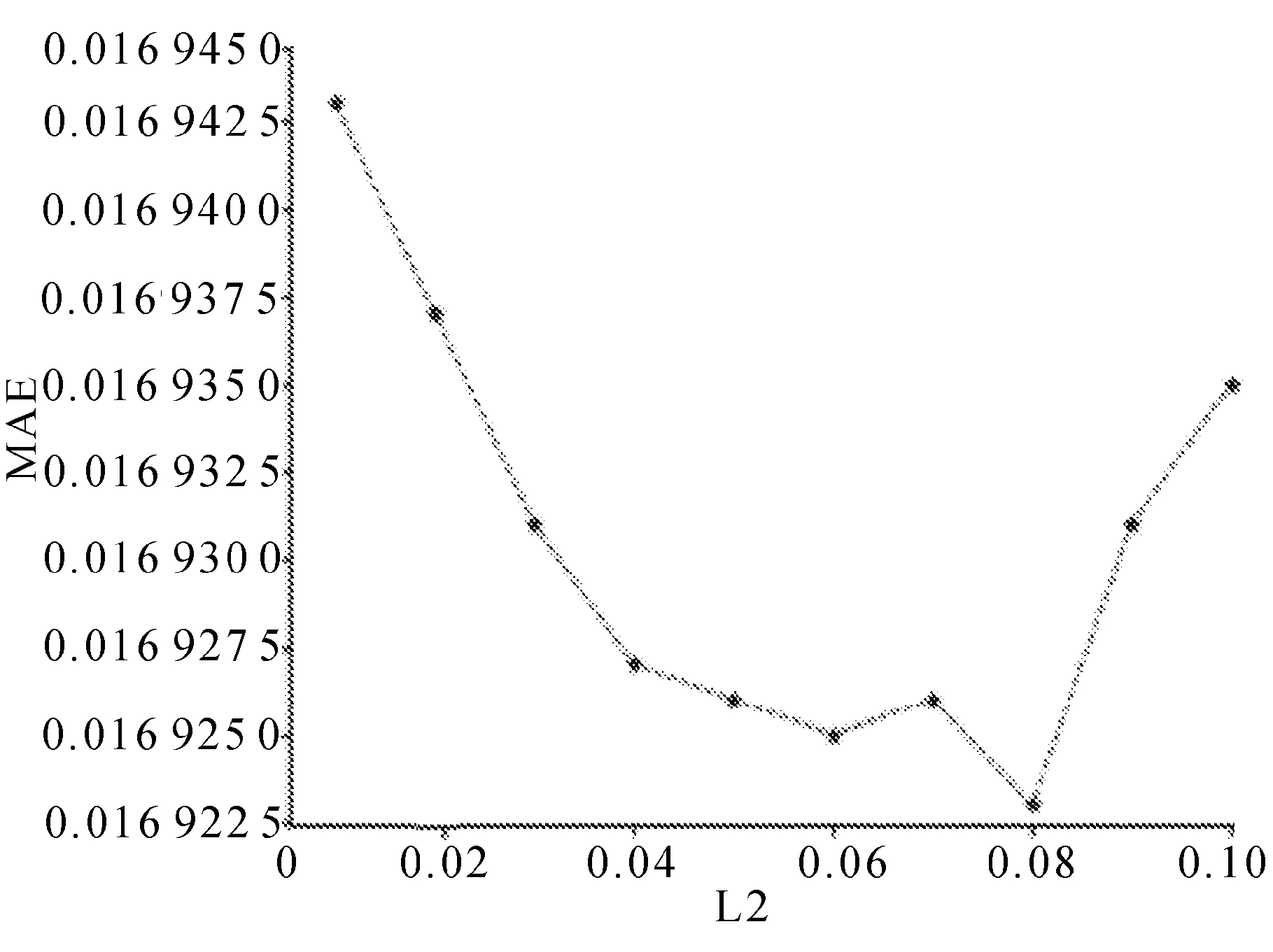
图8 正则化系数对MAE值的影响

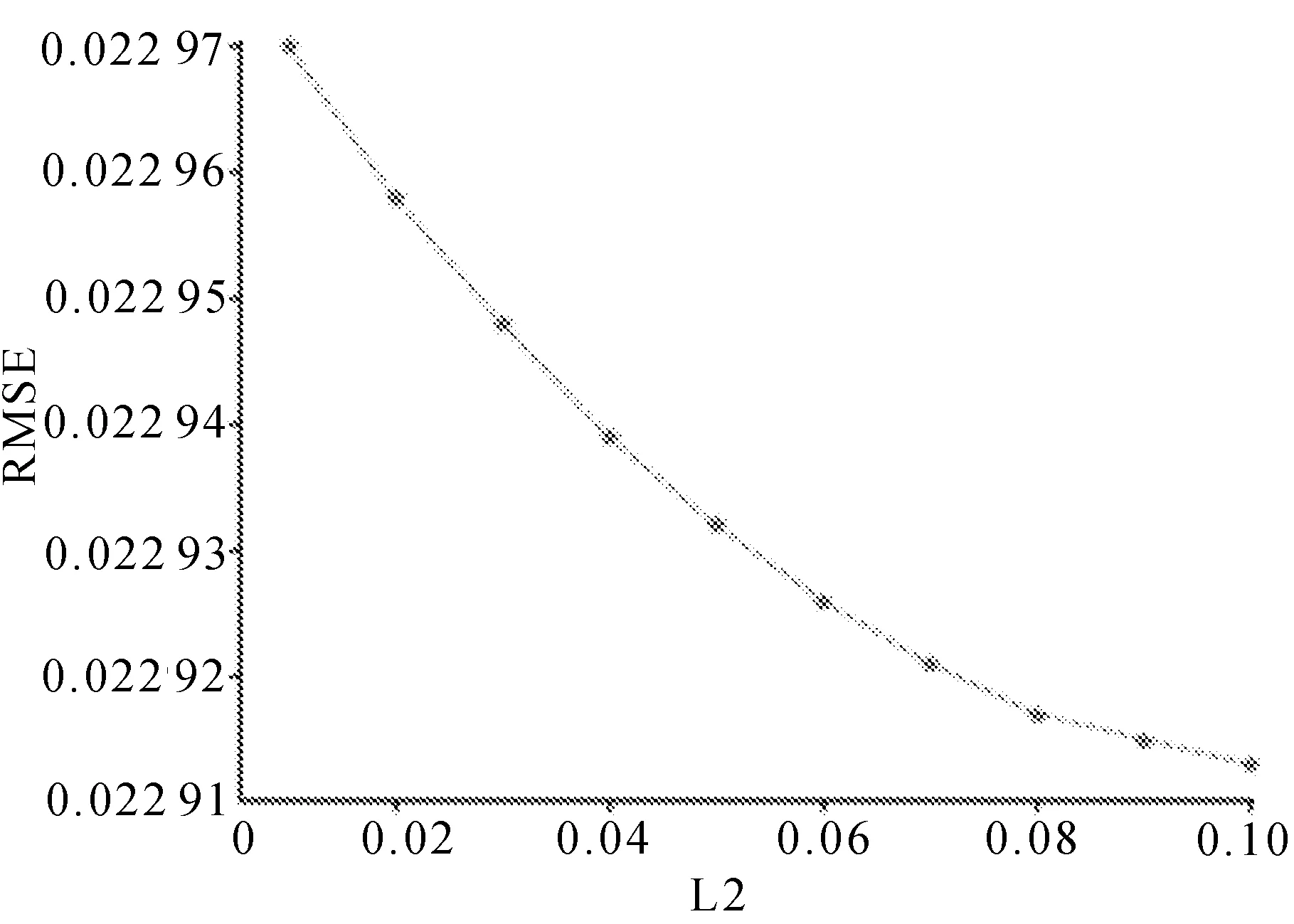
图9 正则化系数对RMSE值的影响

3.4 实验结果

为了验证提出的纵向联邦学习集成算法的个性化贷款模型的准确性,通过对Linear回归、SecureBoost、Poisson回归做五折交叉验证,记录每一次交叉验证预测结果得到的MAE、RMSE值见表2。

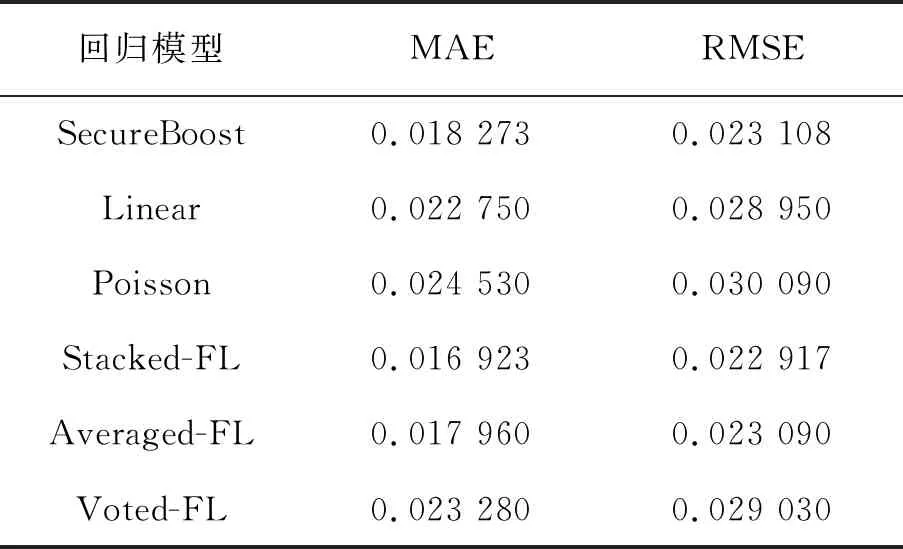
表2 模型预测MAE及RMSE值

计算基学习器交叉验证结果的MAE值与RMSE值,再对其取平均值,作为本实验单个基学习器的最终预测效果,使实验结果更具普遍性。采用Stacking、Voting、Average方法对联邦学习环境下Poisson、SecureBoost、Linear三种算法的验证集和测试集进行集成,Label为利率标签值,Predict_result为Stacked-FL算法计算得到的预测值。

作为传统联邦学习模型的预测效果,基学习器的RMSE值和MAE值分别如图10和图11所示。

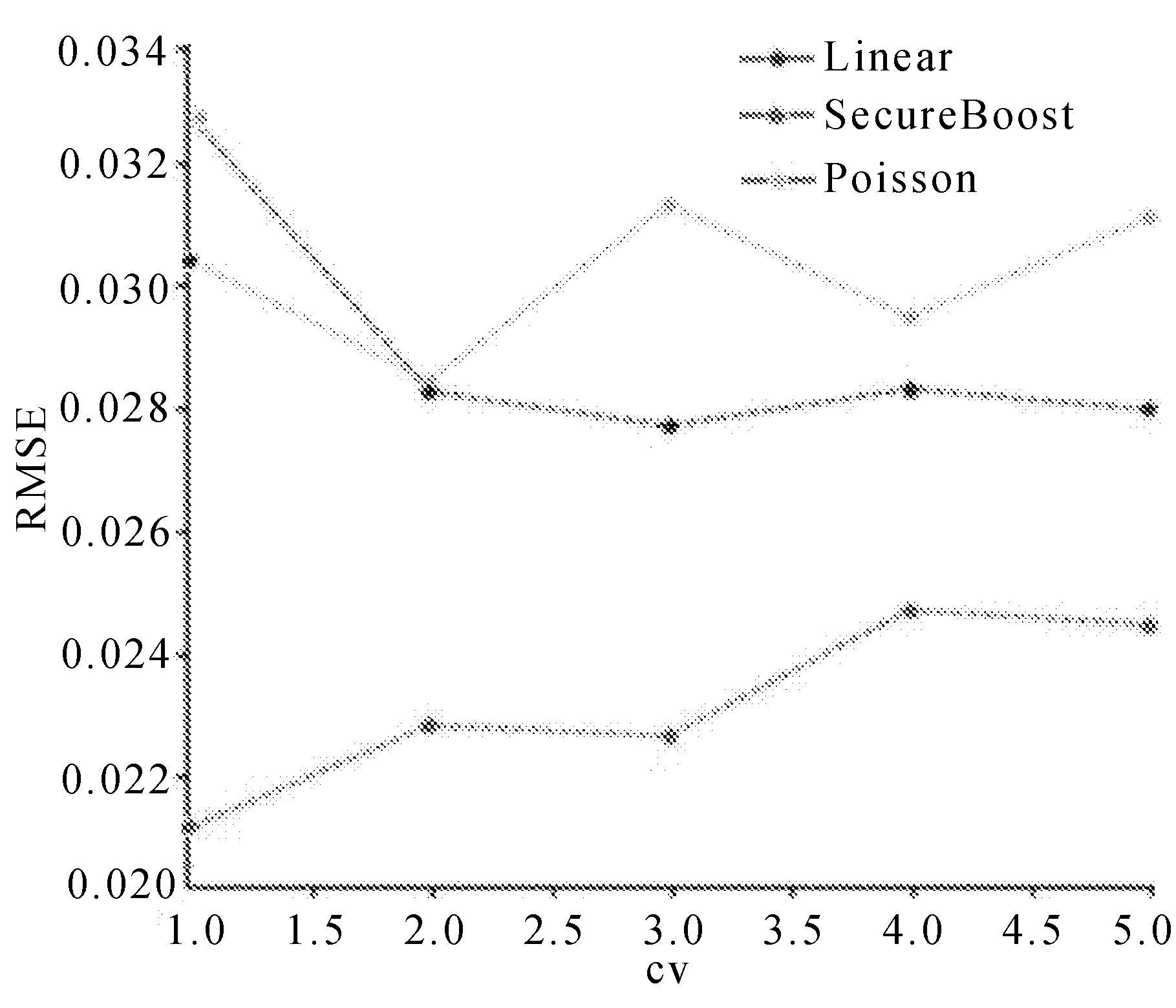
图10 基学习器的RMSE值

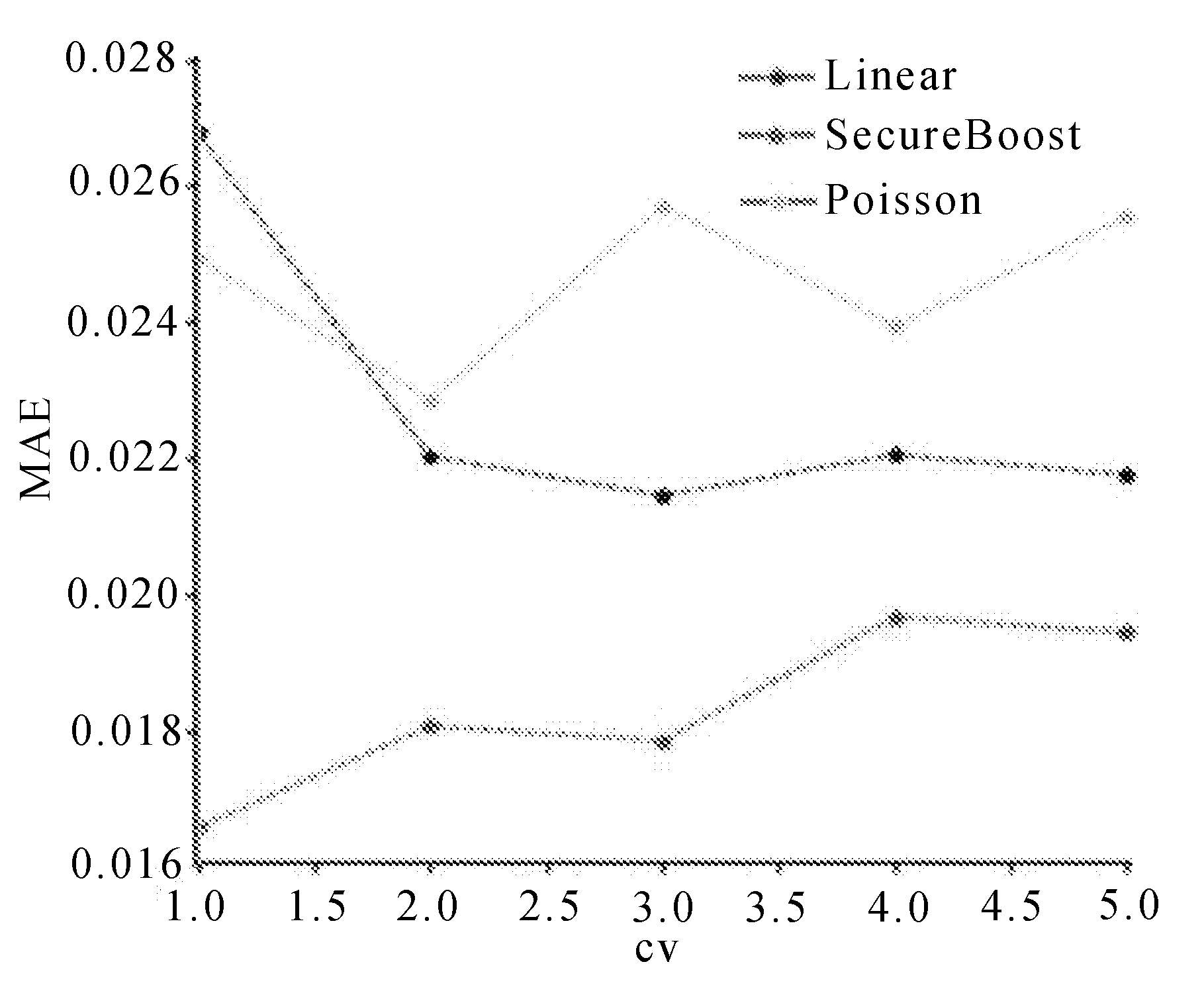
图11 基学习器的MAE值

从图10和图11的整体预测结果分析,SecureBoost模型的均方根误差与平均绝对误差都小于Linear回归和Poisson回归,且SecureBoost误差浮动较小,对模型的预测效果更稳定。

计算集成算法与传统联邦学习算法平均绝对误差、均方根误差表示各模型预测效果,计算结果如图12所示。

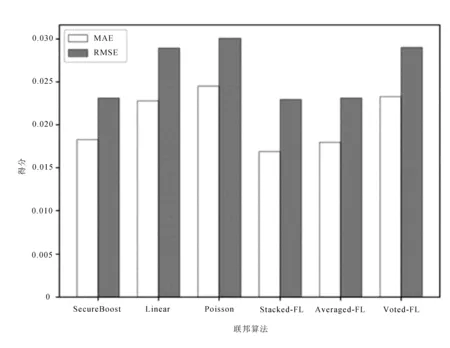
图12 6种联邦算法的MAE及RMSE对比分析

图中,预测均方根误差由小到大分别为Stacked-FL、SecureBoost、Averaged-FL、FL-Linear、Voted-FL、FL-Poisson。平均绝对误差由小到大分别为Stacked-FL、Averaged-FL、SecureBoost、FL-Linear、Voted-FL、FL-Poisson。

3.5 实验结果分析

3.5.1 Stacked-FL准确性分析

为了验证Stacked-FL集成算法的预测准确度,文中采用Stacking方法分别对Poisson、SecureBoost、Linear进行了集成,采用Voting、Average方法作对比实验。将单个联邦算法与FL-Stacking等三个集成算法进行对比,结果见表3。

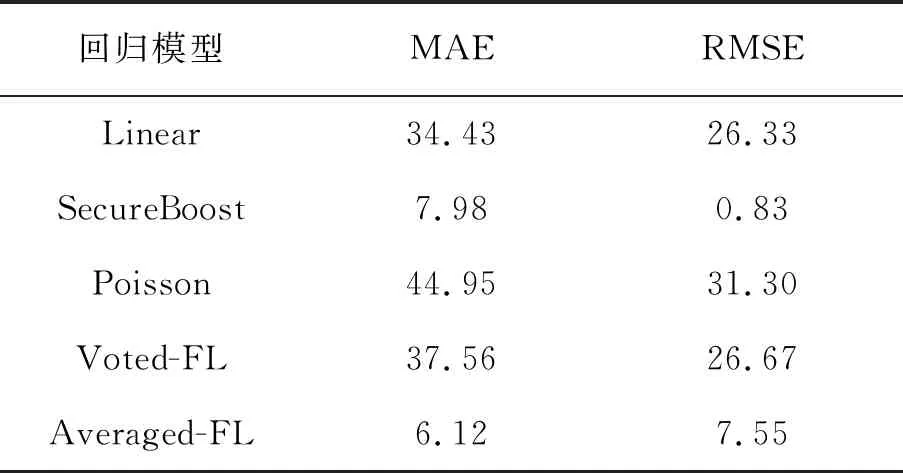
表3 准确性提高比例 %

使用2 578条预测样本对不同模型进行预测,通过实验结果中MAE值与RMSE值显示,FL-Stacking对分散的小维度数据集的训练效果,无论是从模型对异常值的处理上,还是从准确度上都要明显高于其他方法,并且在SecureBoost模型的基础上将MAE值提高7.98%,RMSE值提高0.83%。SecureBoost相对Xgboost可以做到无损应用在联邦学习环境里,所以模型训练效果要优于大多数联邦学习模型。Averaged-FL在准确性上要略高于其他联邦学习模型,并且高于Voted-FL,说明对使用小数据集训练的模型集成效果较好。实验证明,Stacked-FL算法对小数据集训练模型可以提高模型的准确性。

3.5.2 Stacked-FL安全性分析

传统的多元数据处理技术需要将参与方数据集中处理后再训练,在加密聚合过程中,很容易被第三方平台推断出用户信息。针对这一问题,文中提出Stacked-FL对每一方设定为诚实且好奇的,可以良好地遵从安排和调度。

1)每一个参与方的数据始终在本地,不相互流通,并且由数据标签的持有方(任务的发起方)存储整个模型的标签。用传递参数、梯度和损失的方式保障了数据的安全性。

2)计算时,参与方之间会传输加密的中间计算结果用来帮助彼此梯度和损失的计算。传递中间结果采用RSA加密对每个参与方的中间结果进行哈希计算,防止参与方之间交换过程中存在数据安全问题。

3)参与方通过训练过程中梯度和损失的传输过程始终处于加密状态,防止参与方窃取样本数据和通过对应的导数gi和hi去推断用户的隐私。中心服务器为了安全融合各个参与方的本地模型更新梯度采用同态加密的算法,避免第三方窃取训练结果或者泄露中间数据的风险。

3.5.3 Stacked-FL通信负载分析

Stacked-FL的时间复杂度是加密算法、多个基学习器、中心服务器的复杂度之和,所以时间复杂度和空间复杂度会高于传统的融合模型,以消耗更多的通讯资源和计算时间为代价提高模型整体预测的性能。

4 结 语

基于联邦学习的Stacked-FL集成算法的个性化贷款定价模型可以有效地解决中小型银行数据集维度稀疏等问题。采取纵向联邦算法,通过构建数据预处理层、样本对齐层、联邦算法层以及集成算法层提高模型准确性,精准地对不同用户实现个性化定价。中小型银行可以通过这种面向多个参与方的隐私计算方法,联合训练集成模型提高模型的有效性。然而,经过交叉验证以及多个学习器的使用,使整个联邦学习算法的复杂度提高,这会花费很多的通讯成本,也会影响运行效率。在日后的工作中,将尝试对模型通讯效率进行改进,减小通讯成本的开销;采用横向联邦算法联合同领域含有大量重叠特征的企业建模,对数据样本进行扩充,同样得到更精准的模型;在学习器的选择上可以尝试其他选择以及更优的组合。