干形数据采样方法对树干削度方程构建的影响
2023-11-25张兹鹏杨翔玮姜立春
张兹鹏,何 培,杨翔玮,姜立春
(东北林业大学 a.林学院;b.森林生态系统可持续经营教育部重点实验室,黑龙江 哈尔滨 150040)
树干干形变化影响单木材积、材种出材量和生物量[1-2],因此,从干曲线方程到削度方程的研究一直受到林业模型研究者的关注。利用削度方程可以计算树干上任意高度处的直径、任意直径处距树基的高度、树干上任意分段之间的材积和树干总材积[3-5]。削度方程的形式有多种[6-7],但是按照模型形式大致可划分为4类:简单削度方程、分段削度方程、变指数削度方程和三角函数方程[8-9]。
干形数据作为削度方程构建的基础,直接影响模型待估参数的变化,间接影响所建模型的预测精度。针对干形变化的特点,可以将树干区分成若干等长或不等长的区分段,并且通过改变区分段的位置或者数量来获得不同的干形数据[9]。目前,根据已有文献,可以将树干区分段分成以下几种主要类型(在这里不考虑胸径处数据):1)完全等间隔区分段,即从伐桩处开始,每次取固定间隔对树干进行干形测量,通常间隔1 m或2 m[10];2)不完全等间隔区分段,即从某一树高处开始,每次取固定间隔对树干进行干形测量,但在该树高以下增加了区分段的数量,如对树高1 m以下的0.2、0.3或0.6 m处进行干形测量[4,11],或对树高2 m以下的0或0.5 m处进行干形测量[12];3)完全相对高区分段,即只对树干不同相对高处进行干形测量[13],如测量14个不同相对树高(1%、2.5%、5%、7.5%、10%、15%、20%、30%、40%、50%、60%、70%、80%和90%)处的直径[14];4)不完全相对高区分段,这种类型的方法除了对胸径以上不同相对树高处进行干形测量,还测量树干下部0.30、0.46、0.61 m处的直径[15-16]。
在我国,基于树干不同采样数据构建削度方程的研究还未见报道。因此,本研究以大兴安岭落叶松Larixgmelinii为例,在已有干形数据(相对树高0.00、0.02、0.04、0.06、0.08、0.1、0.15、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9 m)的基础上设计了30种数据采样方法,比较不同采样方法对模型预测精度的影响,并结合Tukey多重比较法和树干模拟对基于原始数据和采样数据的削度模型进行综合对比分析,以期通过减少树干上区分段的数量降低外业工作量和成本,提高工作效率。
1 数据与方法
1.1 数 据
落叶松数据采集地点为大兴安岭伊勒呼里山北坡西北部立地亚区,具体位于阿木尔(122°38′30″~124°05′05″E,52°15′03″~53°33′15″N)、西林吉(121°11′22″~123°16′10″E,52°16′58″~53°32′46″N)、图强(121°30′45″~123°29′00″E,52°15′35″~53°33′42″N)、呼中林业局(122°36′58″~124°15′46″E,51°14′51″~52°25′28″N)和漠河林场(122°06′11″~122°27′32″E,53°17′32″~53°03′02″N)。本研究中的落叶松干形数据来源于以上区域的天然林样地,将树木伐倒后测量其胸径、树高及在相对树高0、0.02、0.04、0.06、0.08、0.1、0.15、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9 m处的直径。最终获得落叶松解析木343株,其中树高、胸径的统计量见表1,树高-胸径及相对直径-相对树高的散点图如图1所示。

表1 落叶松样木调查因子统计量Table 1 Descriptive statistics for Larix gmelinii sample trees

图1 树高-胸径、相对直径-相对树高散点Fig.1 Scatter plot of tree height-diameter and relative diameter-relative height
1.2 方 法
1.2.1 削度方程的选择
综合国内外削度方程[8,17-18],本研究选用曾伟生(1997)、Bi(2000)和Max & Burkhart(1976)(简称MB(1976))这3个精度较高的削度方程作为基础模型[8,19-20]。这3个模型为了适应本区域的树种,初步拟合剔除了不显著的参数,最终模型形式如下:
曾伟生(1997):
Bi (2000):
MB (1976):
式中:Z=h/H,t=1.3/H;D为带皮胸径;H为树高;h为树干某处距地面的高度;d为树干h高处的带皮直径;a1~a6为模型待定参数,p1和p2是拐点处的相对高度。
1.2.2 干形数据采样设计
本研究中为了便于描述,将树干上不同高度位置处的直径-树高数据看作不同的采样点,如每株树相对树高0.1处的直径-树高数据称作“点0.1”。一般来说,受树根和树冠效应的影响,树干基部和顶部的干形变化较大,如点0.00和点0.02处的干形;而树干中上部可以看作圆柱体或者截顶抛物线体,这部分的干形变化较小[17]。本研究通过绘制树干曲线图发现,在树干相对高0.2以下干形变化较大,因此以相对树高0.2处为界,设计了5组采样方法。采样方法的具体步骤如下:1)针对相对树高0.2以上的树干部分,即点0.2上面部分选择“固定间隔”的采样方法,间隔20%或30%的相对树高采样,如表2中方法1表示的是舍去点0.2、0.4、0.6和0.8这4处的数据,并以方法1~6为一组;2)针对点0.2下面部分,进行“点数递减”的采样方法,即在第一组方法1~6的基础上舍去点0.1处的数据,得到第2组方法7~12;3)重复“点数递减”的方法,在第1组方法1~6的基础上,舍去点0.08和0.15这2处数据,得到第3组方法13~18;4)在第1组方法1~6的基础上,舍去点0.06、0.1和0.15这3处数据,得到第4组方法19~24;5)在第1组方法1~6的基础上,舍去点0.04、0.06、0.1和0.15这4处数据,得到第5组方法25~30。为了更直观地显示出使用不同采样方法时“点数”的区别,将30种采样方法列出如表2所示。表2中方法0表示的是使用原始数据时的情况。

表2 30种树干采样设计†Table 2 30 kinds of stem sampling designs
1.2.3 模型评价
本研究采用留一交叉验证法(LOOCV)对各模型进行评价[21],具体过程为:1)从全部343株样木的总数据中每次只保留1 株样木数据,下一次不再保留该株样木数据;2)对于其余342株样木中每株树的15个采样点,进行如表2中的不同方法的采样,使用采样后数据对模型进行拟合,并使用拟合得到的参数估计值对保留的1株样木的15处直径进行预测;3)将以上2步过程循环343次,循环结束后得到各样木15个点的直径预测值。最后,通过预测值和实际值来计算确定系数(R2)、平均绝对误差(MAB)、均方根误差(RMSE)和相对百分误差(MPB)。
1.2.4 模型排序
为了便于比较,以曾伟生模型为例,将基于原始数据拟合的模型称为曾0,将基于不同采样方法拟合的模型称为曾i,其中i表示不同的采样方法(i=1,…,30)。当对多个模型进行评价与比较时,需要同时计算多个指标,但各个评价指标的大小往往不统一。因此,本研究使用相对排序法[22],分别计算各模型R2、MAB、RMSE和MPB的相对排序值,其计算公式如下:
式中:Ri为模型i的相对排序值(i=1,2,…,m),其值越小说明该模型的预测效果越好;m为参与排序的模型数;Si为模型i的评价指标值;Smax和Smin分别表示Si的最大值和最小值;
在这个排名系统中,最佳和最差模型的相对排序分别为1和m,其余模型的排序值在1和m之间。另外,MAB、RMSE和MPB这3个指标值越小,代表模型越好,但对于R2则是越大越好,因此为了统一标准,将1-R2作为排序的指标值。最后求出以上4个指标的平均相对排序值,根据排序值Rank越小越好的原则筛选出最优模型。
2 结果与分析
2.1 不同采样设计对曾伟生模型的影响
基于不同采样设计得到的数据,利用R软件GNLS模块对曾伟生模型进行拟合,并使用留一交叉验证法对各采样方法进行评价指标计算,结果见表3。通过比较表中的Rank值可以看出,基于采样数据的曾1~曾30模型中,表现最好的为曾27(Rank=1.585),其次是曾21(Rank=2.054)和曾26(Rank=2.433)。以上3个模型的Rank值均比曾0(Rank=4.618)的小。且相对于基于原始数据的曾0模型,曾27、曾21和曾26的采样点分别减少了8、7和8个。此外也观察到了一个规律,与第一组曾1~曾6模型相比较,即使曾7~曾12模型、曾13~曾18、曾19~曾24和曾25~曾30的点数依次递减,但其检验精度仍在依次提高。如曾1 <曾7<曾13<曾19<曾25。

表3 基于不同采样方法的曾伟生模型的评价结果Table 3 Evaluation results of Zeng model based on different sampling methods
为进一步比较曾0、曾27、曾21和曾26模型之间统计的显著性,基于检验时得到的直径预测值,利用Tukey多重比较法对以上模型进行成对比较。图2表示各模型预测直径时的成对比较。从图2可以看出,模型两两之间在预测落叶松直径时,其置信区间均包含0,说明他们之间均没有显著差异。

图2 曾伟生模型预测直径成对比较Fig.2 Paired comparison diagram of predicted diameters by Zeng model
2.2 不同采样设计对Bi模型的影响
Bi模型的评价指标计算过程同2.1,结果见表4。通过比较表中的Rank值可以看出,在Bi1~Bi30模型中表现最好的为Bi26(Rank=1.455),其次是Bi20(Rank=2.051)和Bi14(Rank=2.706),且以上3个模型的Rank值均比Bi0模型(Rank=2.742)的小。相对于基于原始数据的Bi0模型,Bi26、Bi20和Bi14的采样点分别减少了8、7和6个。同样也观察到了一个和曾伟生模型相同的规律,即与第一组Bi1~Bi6模型相比较,模型Bi7~Bi12、Bi13~Bi18、Bi19~Bi24和Bi25~Bi30的点数依次递减,但其检验精度依次提高。
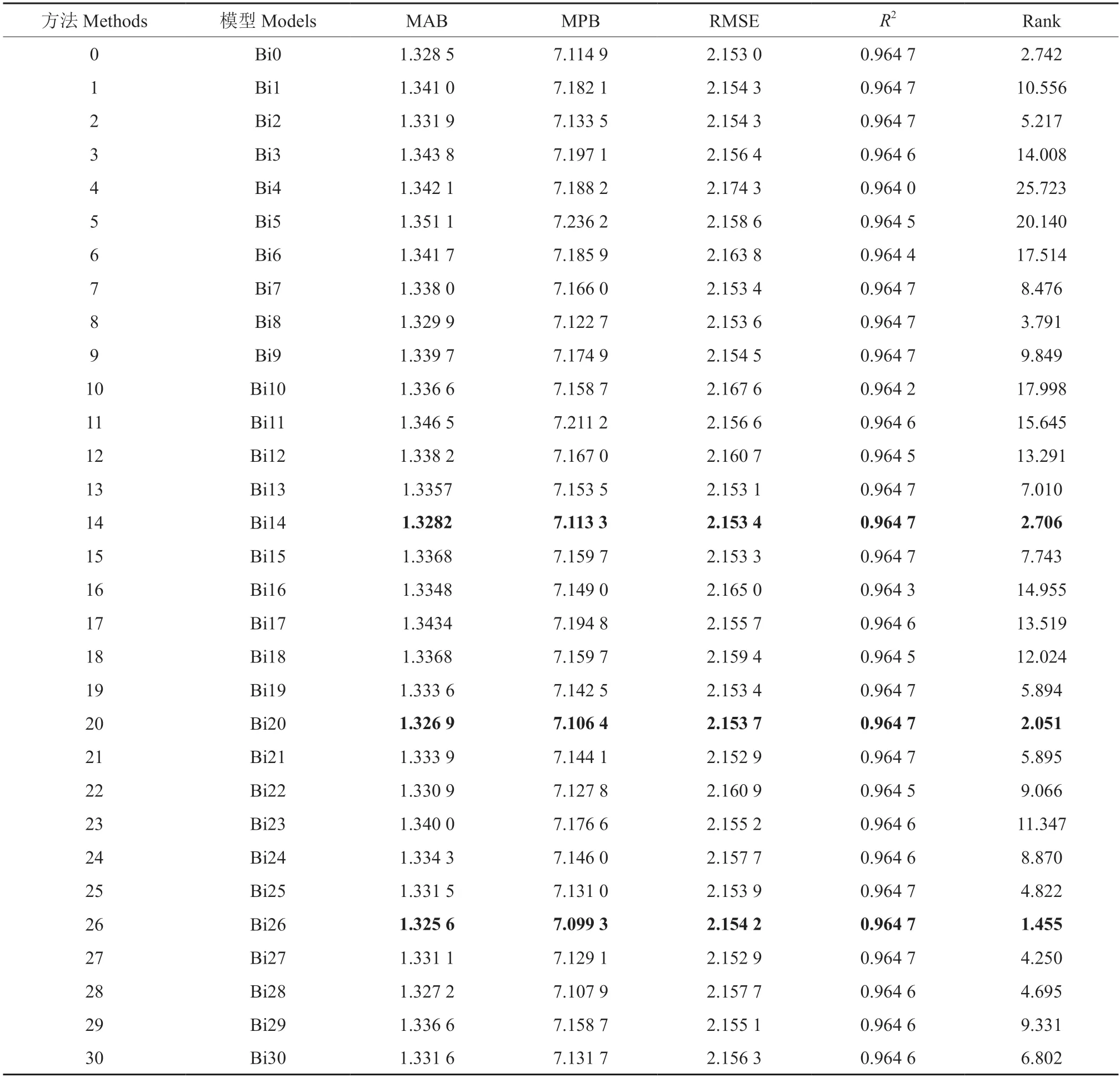
表4 基于不同采样方法的Bi模型的评价结果Table 4 Evaluation results of Bi model based on different sampling methods
基于Tukey多重比较法得到Bi0、Bi26、Bi20和Bi14模型预测直径时的成对比较图(图3)。从图3可以看出,模型两两之间在预测落叶松直径时其置信区间均包含0,说明他们之间也没有显著差异。

图3 Bi模型预测直径成对比较Fig.3 Paired comparison diagram of predicted diameters by Bi model
2.3 不同采样设计对MB模型的影响
MB模型的评价指标计算过程同2.1,结果见表5。通过比较表中的Rank值可以看出,在MB1~MB30模型中表现最好的为MB9(Rank=2.111),其次是MB11(Rank=2.675)和MB7(Rank=2.768),且以上3个模型的Rank值均比MB0模型(Rank=5.840)的小。相对于基于原始数据的MB0模型,MB9、MB11和MB7的采样点分别减少了5、6和5个。基于Tukey多重比较法,得到MB0、MB9、MB11和MB7模型预测直径时的成对比较图(图4)。从图4可以看出,模型两两之间在预测落叶松直径时,其置信区间均包含0,说明他们之间均没有显著差异。

表5 基于不同采样方法的MB模型的评价结果Table 5 Evaluation results of MB model based on different sampling methods
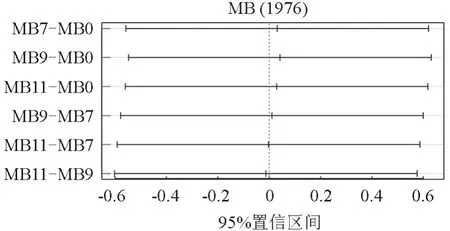
图4 MB模型预测直径成对比较Fig.4 Paired comparison diagram of predicted diameters by MB model
2.4 树干模拟
为了更直观的分析使用采样数据时各模型对树干的模拟效果,对于曾伟生等、Bi和MB模型,分别使用方法27、方法26和方法9对原始数据进行采样,并从落叶松样木中随机抽取一株小树和一株大树进行树干模拟。最后,得到小树的模拟结果如图5(A—C)所示,大树的模拟结果如图5(D—F)所示。从图5可以明显看出,除了图5(C、F)中,基于采样数据的MB9模型在对树干下部拐点附近模拟时与MB0模型稍微有点偏差,其余(A、B、D、E)均显示,使用原始数据时的削度模型,与使用采样数据时的削度模型,对树干的模拟效果几乎相同。
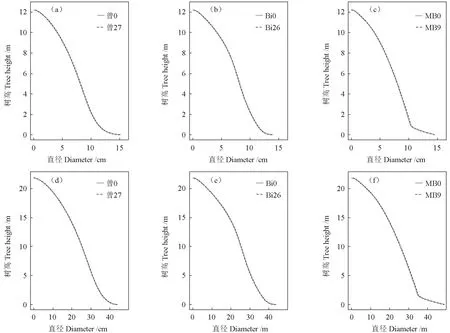
图5 不同削度模型对落叶松小树(A—C)(DBH=10.9 cm,H=12.2 m)和大树(D—F)(DBH =36.7 cm,H=21.8 m)的模拟Fig.5 Simulation of small tree (A—C) (DBH=10.9 cm,H=12.2 m) and large tree (D—F) (DBH=36.7 cm,H= 21.8 m) of L.gmelinii with different taper equations
3 讨 论
由于外业数据获取困难以及人力物力成本高等原因,构建削度方程时设计合理的数据采样方法是十分必要的。到目前为止,国内学者只是按照本研究所提到的某一种区分段来进行干形数据的采集,并没有研究干形测量的位置或数量改变时不同削度模型的变化。本研究在落叶松干形数据(相对树高0、0.02、0.04、0.06、0.08、0.1、0.15、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)基础上,设计了30种采样方法,通过对基于原始数据和采样数据的模型精度进行评价,发现针对不同的削度模型,其适用的采样方法也不同。针对曾伟生等、Bi和MB的模型,检验精度表现最好的分别是方法27、26和9,此时不仅能提高各模型的精度,还能分别减少8、8、5个采样点。Tukey多重比较和树干模拟结果也进一步表明,曾0与曾27模型、Bi0与Bi26模型、MB0与MB9模型之间在预测落叶松树干不同高度处直径时均没有显著差异,且对树干的模拟效果几乎相同。本研究只比较了不同采样方法对曾伟生等、Bi和MB的模型预测精度的影响,对其他模型的影响还有待于进一步深入研究。此外,本研究所用落叶松数据只是来自大兴安岭伊勒呼里山北坡西北部立地亚区的天然林样地,样木基本覆盖了该区域的直径和树高的分布范围。随着数据的积累,对其他区域及其他树种的应用还有待于进一步验证。
4 结 论
为了降低成本和提高工作效率,本研究针对大兴安岭落叶松干形数据的采集给出如下结论:1)如果使用曾伟生等的模型,建议使用第27种采样方法,即只采集树干相对高度0、0.02、0.08、0.3、0.5、0.6、0.9这7处的干形数据;2)如果使用Bi的模型,建议使用第26种采样方法,即只采集树干相对高度0、0.02、0.08、0.3、0.4、0.6、0.9这7处的干形数据;3)如果使用MB的模型,建议使用第9种采样方法,即只采集树干相对高度0、0.02、0.04、0.06、0.08、0.15、0.3、0.5、0.6、0.9这10处的干形数据;4)如果同时考虑以上3种模型,建议使用第20种采样方法,即只采集树干相对高度0、0.02、0.04、0.08、0.3、0.4、0.6、0.9这8处的干形数据,此时3个模型对落叶松树干不同位置处直径的预测精度均略有提高。
