随机变分不等式的二阶微分方程方法

庄慧婷，王莉，孙菊贺，贾丹娜，袁艳红

（1. 沈阳航空航天大学 理学院，沈阳 110136；2. 太原理工大学 经济管理学院，太原 030024）

变分不等式是数学领域的一个重要分支。经过几十年的研究与发展，变分不等式的理论和算法研究已经趋于成熟，并在多个学科中有所应用。变分不等式的研究主要集中于解的存在条件［1-2］、迭代算法及收敛条件［3-5］，并在经济、交通、工程等领域有广泛应用［6-8］。基于此，该问题得到了越来越多研究者的关注。

Ferguson等［9］在1956年提出了随机规划问题，而随机变分不等式问题作为随机规划的一个重要分支，在经济分析、交通均衡、能源建模等领域［10-11］都有着广泛的应用，更多关于随机规划知识的介绍见文献［12］。基于此，随机变分不等式问题成为近年来的研究热点之一［13-15］。本文将研究随机变分不等式问题，求解x∈C，使得

式中：Rn为n维实数空间；f(·，ξ)对任意ξ是局部Lipschitz连续。对每一个固定的η和ς，函数h(·，η)：Rn×Ω→Rl和g(·，ς)：Rn×Ω→Rm均是连续可微的凸函数。ξ、η和ς是定义在概率空间(Ω，F，P)上的随机变量，F是Sigma代数，P是定义在Ω上的概率测度。

显然，随机变分不等式问题中存在着随机变量，即该问题中可能存在不确定因素。随着时代的发展，人们越来越重视对实际问题中一些不确定性风险的预测和处理，特别是在经济金融、工程应用和决策科学等领域中所涉及的很多因素都是不确定的，因此研究包含的随机因素优化问题更符合实际意义。近年来，随机变分不等式作为处理不确定环境下最优化问题和博弈论的重要方法之一，受到了广泛的关注和研究。

Facchinei等［16］对变分不等式问题和互补问题的基本理论和应用进行了全面的介绍和总结，该书被认为是最优化领域中最有价值的工作，记录了变分不等式和互补问题很大一部分重要结果，但是却没有记录微分方程方法求解变分不等式的理论。因此，应用微分方程方法求解变分不等式这一问题的研究还远未深入，这部分内容还需要进一步补充，这也是本文将要讨论的主要问题。

受到Attouch等［17］的启发，利用二阶微分方程系统求解随机变分不等式问题（1）是一个新的思想。在上述研究成果的基础之上，本文将研究求解随机变分不等式问题（1）的二阶微分方程方法。许多文献的数值结果表明SAA方法是一种有效的求解随机问题的方法［18-19］，所以本文将运用互补函数和SAA方法将原始问题等价转换成方程组，利用该方程组建立具有正黏性阻尼系数γ(t)和时间尺度系数β(t)的二阶微分方程系统。然后进一步研究该二阶微分方程系统的收敛性和收敛速度。最后，给出两个数值实验说明该二阶微分方程系统求解随机变分不等式问题的有效性。

为了建立随机变分不等式的二阶微分方程系统，首先介绍下面的概念与相关性质。

定理1［17］设H是希尔伯特（Hilbert）空间，Φ：H→R是凸的连续可微的函数，其梯度∇Φ是Lipschitz连续的。

若β，γ：[t0，+∞)→R+，且g：[t0，+∞)→H

是局部可积的，则二阶微分方程系统

定义1［17］如果映射ϕ：Rn×Rn→Rn，满足x∈Rn，y∈Rn，xTy=0⇔ϕ(x，y)=0，则称ϕ(x，y)为Rn上的互补函数。特别地，NR函数)就是一类互补函数，将NR函数光滑化后可得光滑的NR函数为。

1 随机变分不等式的转化

由优化理论不难得到SVIP问题可以等价为-E[f(x，ξ)]≥0。因此，SVIP问题的KKT条件为

L(x，μ，λ)=E[f(x，ξ)]+JxE[h(x，η)]Tμ+JxE[g(x，ς)]Tλ（JxF(x，y)T表示对函数F(x，y)中的变量x所求得的Jacobian矩阵的转置表示SVIP问题的拉格朗日函数。由SAA方法，问题（1）可以转化为如下问题：找到x∈CN，使得

其中约束集合CN表示为

其中

根据互补函数的定义1，设S：R×Rn×Rl×Rm→R×Rn×Rl×Rm，z=(ε，x，μ，λ)∈R×Rn×Rl×Rm，则SAA问题的KKT条件（6）可以转化为如下的光滑化方程

运用光滑化的NR函数和SAA方法将原SVIP问题（1）转化为光滑化方程组（7），下一节将运用光滑方程组（7）建立二阶微分方程系统。

2 随机变分不等式的二阶微分方程方法

由于原SVIP问题（1）转化为光滑化方程组（7），为了求解方程组（7）的值，定义函数，考虑下面的凸优化问题

则有

首先假设以下条件成立：

（1）Φ(z)=为凸函数，P=argminΦ非空；（2）γ和→R+为非负连续函数；（3）t0＞0是初始时间。建立二阶微分方程系统如下

式中：∇Φ：R→R为Φ的梯度，还有两个随时间变化的参数分别为：γ(t)是正黏性阻尼系数，β(t)是时间尺度系数。根据定理1可知，该方程存在唯一的全局解。在平凡情况Φ(z)=≡0时，上述二阶微分方程系统（11）可直接积分得到

设二阶微分方程系统（11）满足以下假设条件

在该假设条件下，可以定义函数Γ：

Γ(t)的定义不依赖于初始时间t0的选择，当t0→+∞时，可以得到=γ(t)Γ(t)-1。

定义全局能量函数如下

以及锚点函数

有了上述三类函数，下面定义函数χ：，该函数在二阶微分方程系统（11）的收敛性定理的证明过程中起着重要的作用。具体形式如下

根据内积与范数的关系，上式的右边可以化为

显然，χ(·)是一个非负函数且是递减的。运用函数χ(·)可以得到二阶微分方程系统式（11）的收敛性定理，该定理也给出了收敛率的估计。

定理2设Φ(z)=为凸函数，P=argminΦ非空，β，γ：)

[t0，+∞→R+为非负连续函数，且满足假设条件(H)0，并满足以下增长条件(H)γ，β

则对于二阶微分方程系统（11）的轨迹z(t)=(ε(t)，x(t)，μ(t)，λ(t))∈R×Rn×Rl×Rm满足以下收敛性

此外，可以得到该轨迹z(t)=(ε(t)，x(t)，μ(t)，λ(t))在[t0，+∞)上是有界的。

证明：设m=，为了计算χ(·)的导数，首先计算能量函数W和锚点函数h的导数

结合以上结果，可以得到

因此，由假设(H)γ，β可以推断出χ̇(t)≤0。所以在[t0，+∞)上有χ(t)≤χ(t0)，根据χ(t)的公式可以得到对于所有的t＞t0有

此外，证明

在[t0，+∞)上仍为有界的，由χ(·)的公式和递减性，可得

q(t)=可得{q(t)|t≥t0}是有界的，因为＜+∞。将（17）除以p(t)，又因为=q(t)，且C=χ(t0)，可得

因为q̇(t)=，所以有C)≤0，再除以q(t)2后，可得

上式积分后可得：对于某些c1＞0，有h(t)≤c1(1+q(t))。

因此z(t)=(ε(t)，x(t)，μ(t)，λ(t))在)[t0，+∞上有界，证毕。

3 数值实验

数值实验采用Matlab9.0编写，常微分方程求解采用龙格-库塔ode 45。在实验中，选取系数γ(t)=，α=25和β(t)≡1。

例1考虑随机变分不等式问题（1），其中

和

式中：ξ服从均值为1、方差为1的正态分布；ς是[0，1]上的随机分布；该问题的最优解为x＊=(3.0000，1.5708，1.0000)。本实验中取初始点分别为ε0==0.0001，x0=(3，1，1)，λ0=(-0.5，-0.1，-0.1)。

表1总结了运用二阶微分方程系统（11）求解例1的数值结果。图1中给出了从所给的初始点出发，二阶微分方程系统（11）求解例1所得到的解的轨迹x(t)。

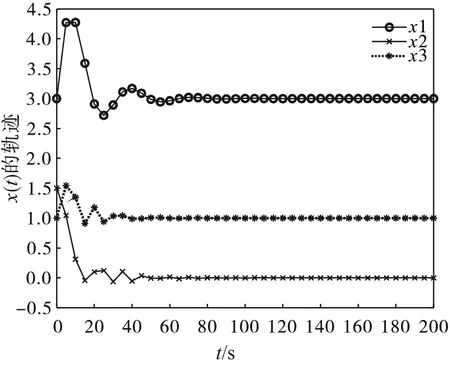
图1 例1的二阶微分方程系统（11）从初始点出发的x（t）轨迹曲线

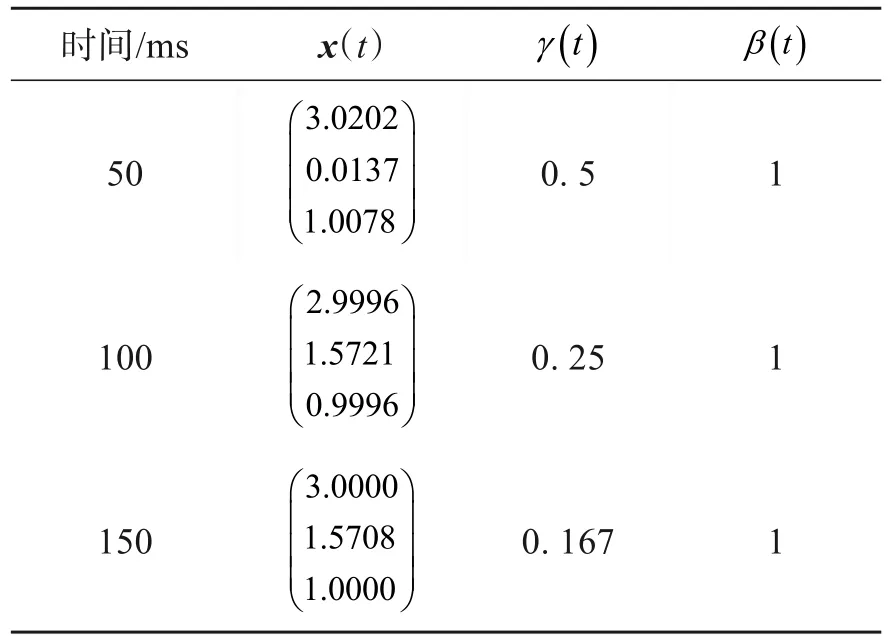
表1 例1的二阶微分方程系统（11）的数值结果

例2 考虑随机变分不等式问题（1），其中

式中：ξ服从均值为1，方差为1的正态分布；ς是[0，1]上的随机分布；该问题的最优解为x＊=(5，1.57，1，0，1)。本实验中取初始点分别为ε0==0.000 1，x0=(3，1，1，0，0)，λ0=(-0.5，-0.1，-0.1，0，0)。

在表2中总结了运用二阶微分方程系统（11）求解例2的数值结果。图2中给出了从所给的初始点出发，二阶微分方程系统（11）求解例2所得到的解的轨迹x(t)。

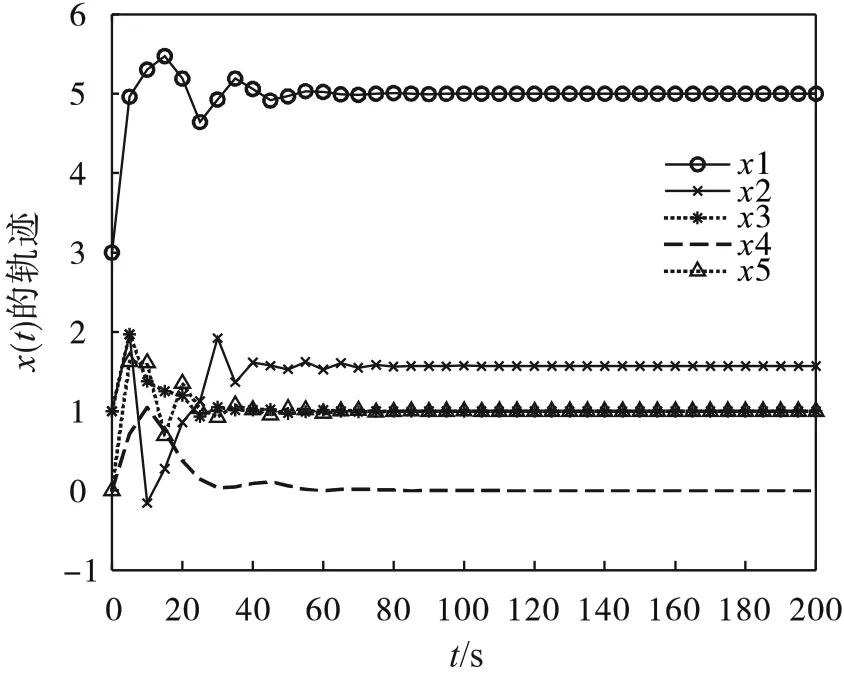
图2 例2的二阶微分方程系统（11）从初始点出发的x（t）轨迹曲线

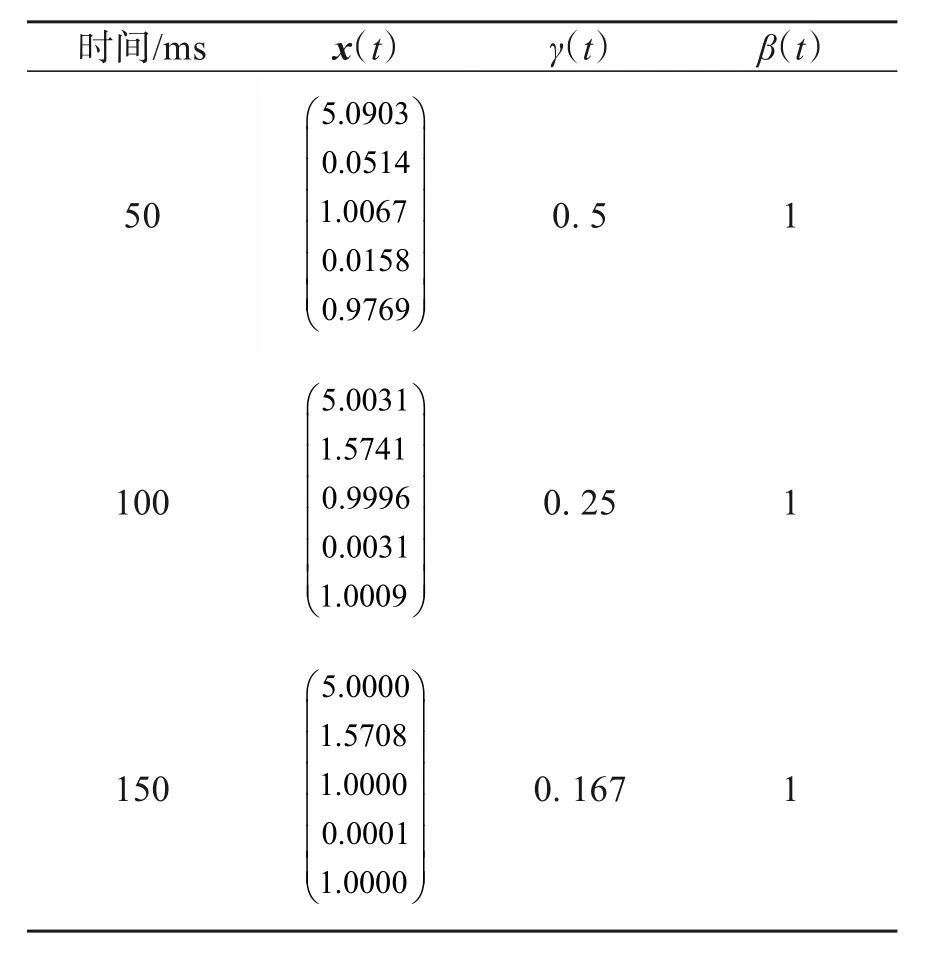
表2 例2的二阶微分方程系统（11）的数值结果

4 结论

本文首次采用Attouch等［17］提出的基于惯性阻尼系数γ(t)和时间标度系数β(t)的二阶微分方程系统来求解随机变分不等式问题（1），得到了该二阶微分方程系统轨迹的收敛性和收敛速度，并研究了在γ(t)和β(t)影响下解的收敛性质。除了理论结果外，本文还给出两个数值算例说明二阶微分方程系统在求解随机变分不等式问题中的有效性。