基于无迹卡尔曼滤波的BDS/INS组合定位方法

王尔申，朱骏，徐嵩，杨健，宋建，陈昌龙，刘依凡

（沈阳航空航天大学 a.电子信息工程学院， b.辽宁通用航空研究院，沈阳 110136）

惯性导航系统 INS具有自主性好、数据更新率高、抗干扰能力强等优点，但是导航误差存在随时间积累的问题［1］。全球导航卫星系统（global navigation satellite system， GNSS）能够提供全球、全天候、高精度导航定位授时信息，但易受无线电干扰［2］。组合导航系统利用两种或两种以上的导航设备提供多重信息，构成定位鲁棒性更强的系统［3］。北斗卫星导航系统（BDS）是我国自主建设、独立运行的全球卫星导航系统［4］，将惯导与北斗定位进行组合，发挥系统各自优势，成为组合导航技术研究的热点。组合导航的组合方式分为松组合、紧组合以及深组合［5］。松组合结构简单，BDS和INS可以独立工作，使用BDS数据修正INS；BDS和INS紧组合是伪距及伪距率的组合［6］；深组合又称超紧组合，是将INS的测量值反馈给BDS，以组合滤波后的导航信息修正INS［7］。

近年来，研究人员采用不同的算法线性化组合导航数学模型，从而提高组合导航的精度。目前，常见的组合导航滤波算法主要有扩展卡尔曼滤波［8］EKF、无迹卡尔曼滤波［9］UKF、粒子滤波［10］（particle filter，PF）等，而 UKF 因无需计算雅可比矩阵，具有高精度及方便实现的特性，在组合导航数据融合算法中脱颖而出 。本文主要研究松组合，并将基于UKF的组合导航定位结果与基于EKF得到的结果进行比较，验证了不同组合导航算法对定位精度的影响。

1 无迹卡尔曼滤波

扩展卡尔曼滤波EKF解决了经典卡尔曼滤波不能应用于非线性系统的问题［11-12］，但扩展卡尔曼滤波要求噪声服从高斯概率分布等［13］。无迹卡尔曼滤波UKF采用无迹变换（unscented transform， UT）的方法，对得到的确定的样本点（Sigma点）进行非线性变换处理，是一种基于确定性采样的非线性滤波算法［14］。离散非线性系统状态方程和观测方程如式（1）和式（2）所示

式中：xk为n维状态向量；Wk为p维系统噪声；Vk为q维量测噪声。

针对组合导航的状态方程，在UKF滤波算法中需要对状态进行扩维处理，状态矢量经扩维后变为：，则的状态协方差阵为

UKF的时间更新方程为

UKF的量测更新方程为

根据组合导航系统的状态方程和量测方程，设定一定的滤波初值，利用上述的UKF滤波算法能够获得第k时刻的系统状态估计值(k=1，2，3，4，…)。

2 基于无迹卡尔曼滤波的BDS/INS组合导航系统设计

2.1 BDS/INS空间杆臂误差模型与时间不同步误差模型

惯性导航系统一般将导航定位的参考基准设置为惯性元件的几何中心，然而卫星导航的参考基准通常为接收机天线的相位中心，当实际运载体中同时使用多种导航系统时，它们的安装位置会存在一定的偏差［15］。为将不同导航系统的导航信息进行比对和融合，需考虑空间杆臂误差。

设惯性元件相对于地心的矢量为R，北斗卫星接收机天线相位中心相对于地心的矢量为r，天线相位中心相对于惯性元件的矢量δl称为杆臂距离，三者之间的矢量关系满足

因接收机天线和惯性元件的安装位置通常固定不动，所以杆臂距离δl在惯性元件坐标系下为常矢量，将公式（15）两边相对地球坐标系求导，可得公式（16），其中记ven(BDS)为卫星天线的地速，ven(INS)为惯导的地速

由于杆臂距离一般在米量级，所以两种导航坐标系之间的角度差非常小，近似认为，则杆臂速度误差、位置误差δpGL如下所示。式中矩阵表示载体坐标系相对于导航坐标系的姿态阵；为载体坐标系相对于地球坐标系的角速度；LINS为惯导定位经度；RMh、RNh分别为子午圈主曲率半径和卯酉圈主曲率半径。

在BDS/INS组合导航系统中，计算传感器导航信息的时刻通常与传感器实际的信息采集时刻不同，从传感器信息采集到组合导航计算之间存在一定的时间滞后。文中在组合导航系统建立时，将对时间不同步误差进行估计和补偿。

如图1所示，INS和BDS两类传感器相对组合导航计算滞后的时间一般并不相同，将两者之间的相对滞后记为时间不同步误差δt，可以得到惯导速度和卫星速度之间的关系为

图1 时间不同步误差

式中：an是载体在不同步时间δt附近的平均线加速度，如公式（21）所示

3.2 BDS/INS组合导航系统模型

文中建立状态方程在传统的15维状态向量的基础上，考虑到空间杆臂误差与时间不同步误差，将系统状态向量扩大到19维。即导航系统误差状态变量由姿态角误差φ、速度误差δv、位置误差(δL、δλ、δh)、陀螺仪漂移误差ε、加速度计零偏误差∇、空间杆臂误差δl和时间不同步误差δt组成，误差状态向量如式（24）所示

导航系统的误差状态方程如式（25）所示

式中：XI(t)为系统状态变量；FI(t)为状态转移矩阵；WI(t)为系统噪声矩阵；GI(t)为噪声驱动矩阵；系统的转移矩阵FI(t)为19×19维的矩阵。

松组合导航方式有两组观测值，分别是BDS和INS输出的位置差值和速度差值。Vp和VV为BDS接收机沿坐标系3个轴方向上的位置与速度误差，则位置量测与速度量测方程为

3 BDS/INS组合导航算法实验分析

3.1 实测数据采集实验平台

为了验证基于无迹卡尔曼滤波的BDS/INS组合导航方法的性能，本文通过组合导航开发系统，采集真实数据进行组合导航算法实验验证。实验数据采集设备使用组合导航平台ZH3000A-OEM-ED，该平台配置有高性能的板载惯性测量单元IMU和高精度GNSS双天线接收板卡，能够输出BDS和IMU数据，支持高精度RTK定位。实验在体育场跑道上进行，在实验数据采集过程中，进行了加速、减速和转弯等机动性运动，实验轨迹如图2所示。

图2 实验数据采集轨迹

3.3 算法验证与结果分析

针对EKF与UKF两种滤波模型，采用实测数据进行组合导航数据融合实验。本文选取了其中420 s的实验数据用于算法验证，采用实验仪器配套的组合导航处理软件的高精度定位结果作为参考值，将两组实验的导航结果与参考值进行比较，分析不同滤波算法在组合导航系统中的性能。基于EKF算法的组合导航速度误差和位置误差如图3所示，而基于EKF算法的组合导航速度误差和位置误差如图4所示。通过对两种滤波方法的误差比较可以得出：EKF算法的东向、北向速度误差在4 m/s的范围内，而UKF算法的东向、北向速度误差控制在2 m/s的范围；EKF算法的经度、纬度误差在20 m左右，而UKF算法的经度、纬度速度误差控制在5 m的范围内。

图3 EKF误差

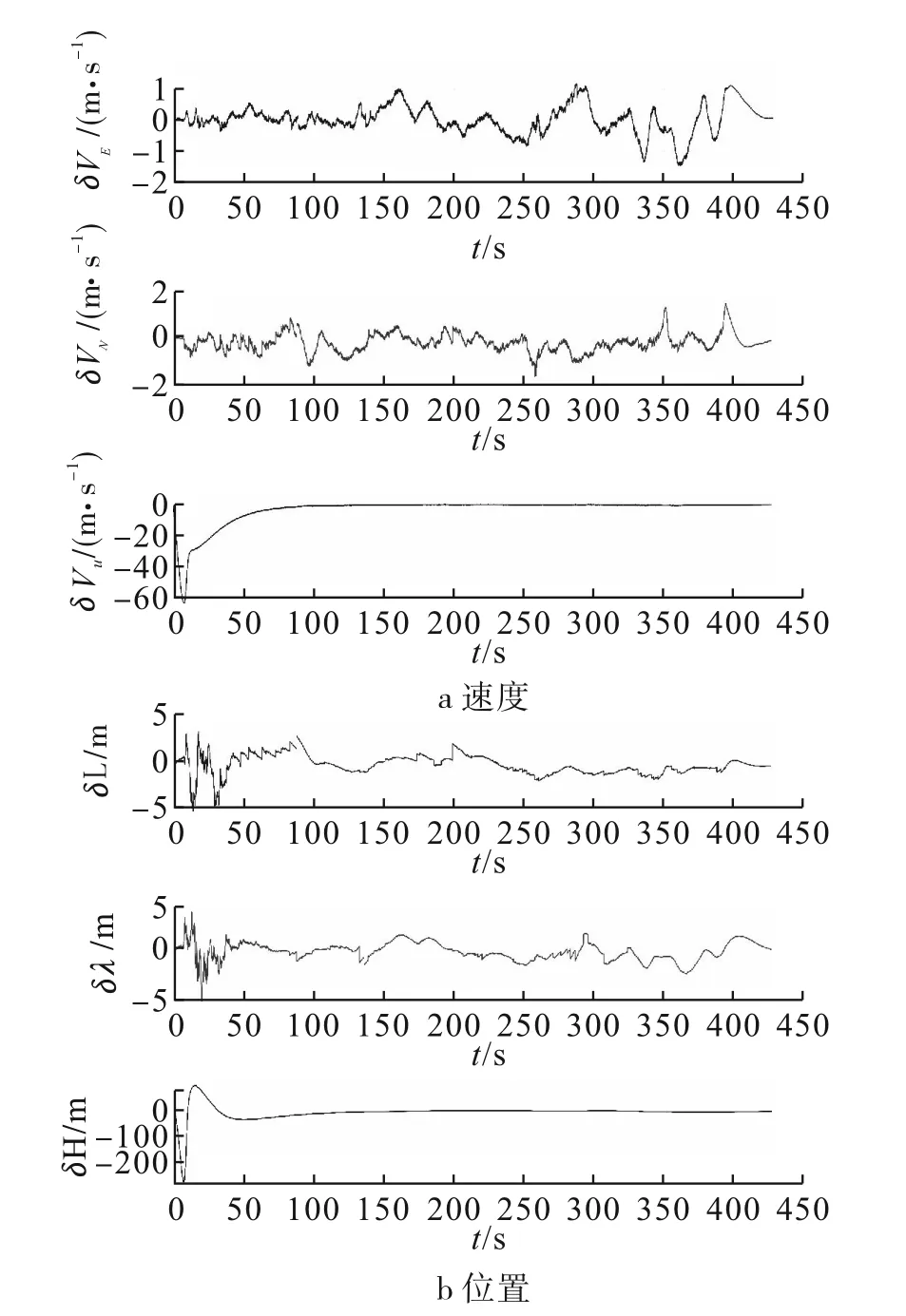
图4 UKF误差

两种滤波算法定位结果的误差特性统计表和经纬度轨迹对比图如表1和图5所示。

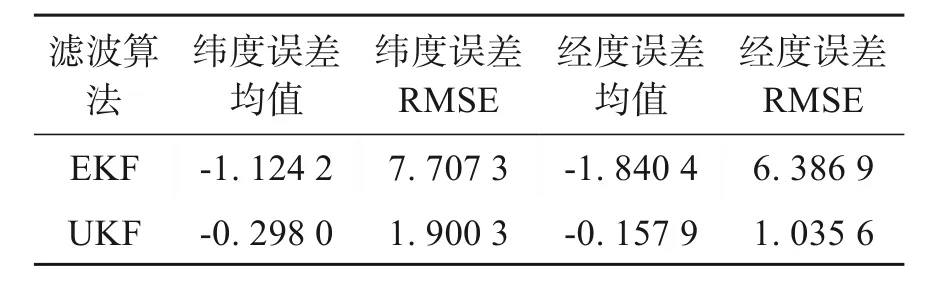
表1 组合定位误差分析 m

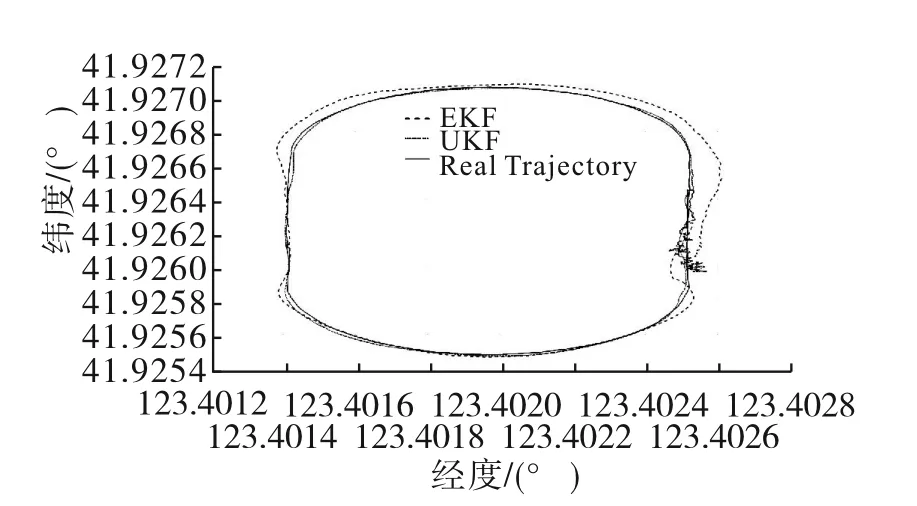
图5 经纬度轨迹对比

通过表1分析得出，UKF算法相比EKF算法定位误差明显减小，纬度和经度的均值分别减小73.5%和91.4%，均方根误差分别减小75.3%和83.8%。由图5看出，UKF算法的经纬度轨迹与参考系统输出的经纬度信息变化趋势接近，且误差与EKF算法相比更小。

4 结论

文中研究了无迹卡尔曼滤波BDS/INS组合导航定位算法，将传统15维状态向量扩展到19维，并采用无迹卡尔曼滤波算法对导航信息进行处理。利用组合导航平台采集实测数据，验证组合导航EKF、UKF滤波算法的性能。验证结果表明：本文的组合导航定位算法相比EKF算法在组合导航定位经纬度参数上的均方根误差分别减小了83.8%与75.3%，较好地提升了组合导航定位精度。