基于马尔科夫毯的近似函数依赖挖掘算法

夏秀峰，刘朝辉，张安珍

（沈阳航空航天大学 计算机学院，沈阳 110136）

数据分析最重要的任务之一是发现给定数据集中的函数依赖关系，在数据集成、数据清洗［1］、知识发现［2］、数据质量评估等相关领域有着广泛应用。函数依赖（functional depen‐dency，FD）是数据集中属性之间的一种依赖关系。对于给定数据集和两个属性集合X和A，若任意元组对在X中的属性取值相同，在A中属性取值也相同，则称X→A是一个函数依赖。本文只考虑挖掘非平凡且最小的函数依赖，即A不包含于X，且X删去任意一个子集B后，函数依赖XB→A不再成立。然而，实际数据往往存在各种错误，这些错误可能导致原本正确的函数依赖不再成立，无法出现在挖掘结果中，从而影响函数依赖挖掘结果的召回率。因此，研究人员提出了近似函数依赖挖掘算法，其核心思想是在适当放宽函数依赖的成立条件下，允许数据中存在少量违反函数依赖的元组对，从而在一定程度上降低了数据错误对函数依赖挖掘算法召回率的影响。例如，文献［3］将所有元组对中违反函数依赖的元组对所占比例定义为函数依赖的误差，并挖掘出误差小于给定阈值的近似函数依赖。

根据近似函数依赖挖掘算法的性质，可以分为行高效算法、列高效算法以及混合式算法。行高效的代表算法有Tane［4］、Fun［5］、FD_Mine［6］和Dfd［7］，它们将函数依赖的候选集建模为属性组合的幂集格，通过遍历得到最小且非平凡的函数依赖。虽然这4种算法的遍历策略不同，但是都连续生成候选的函数依赖，并使用位置列表索引中的剥离分区验证候选的函数依赖。Tane、Fun、FD_Mine算法使用基于先验候选生成原则，由搜索候选格自底向上进行遍历，Dfd算法使用深度优先随机游走的遍历策略。然而，这类算法的搜索空间是属性数量的指数级，在属性数量较多的数据集中表现不佳。列高效的代表算法有Fdep［8］，Dep-Miner［9］，FastFDs［10］，核心思想是两两比较所有元组，找出非函数依赖，然后利用非函数依赖推导出候选函数依赖，这类方法需要对全部数据进行两两比较，时间开销为O（n2），对于元组较多的数据集表现较差。混合式算法HYFD［11］结合了行高效以及列高效的优点，在第一阶段使用采样对部分元组提取非函数依赖；然后在第二阶段对第一阶段得到的函数依赖候选集进行验证。针对这两个阶段的切换标准是基于采样和验证标准的度量方法，如果切换过早，与直接利用搜索算法无异；切换过晚，无异于直接利用归纳技术，都会非常耗时。

现有的近似函数依赖挖掘方法虽然可以降低数据错误对函数依赖挖掘结果的影响，但仍然存在以下两方面的问题：（1）现有方法大多需要系统地枚举所有可能的FD，并逐一验证其共现频率是否满足阈值要求，导致候选FD规模巨大，挖掘效率较低。例如，假设数据中有m个属性，文献［3］的搜索空间为O（2m），搜索代价是指数级的；（2）现有的方法容易出现过拟合问题，挖掘出大量左部属性数量较多的虚假FD，挖掘结果准确率较低。例如，对于只有几十个属性的数据集，基于共现频率的方法会挖掘出成百上千条FD，其中大部分是过拟合的。

为了解决以上问题，本文提出了基于马尔科夫毯的近似函数依赖挖掘算法。该算法利用马尔科夫毯的条件独立性推导候选函数依赖，从而减少候选函数依赖的规模，在保证挖掘出最小且非平凡的近似函数依赖的同时，不会出现过拟合情况。具体算法流程如下：首先，对输入数据集进行采样，在样本上学习贝叶斯网络结构，得到每个属性的马尔科夫毯；其次，根据每个属性的马尔科夫毯创建其左部决定集的搜索空间；最后，对于搜索空间中最大候选函数依赖不断向下泛化验证，得到误差小于给定错误阈值的最小且非平凡的近似函数依赖。通过引入马尔科夫毯的条件独立性，该算法可以有效减少候选函数依赖的规模，并且避免了过拟合问题，从而提高了近似函数依赖挖掘的效率和准确性。

1 先验知识和问题定义

1.1 函数依赖

定义1 函数依赖：给定属性集U，关系模式为R，X和A是U的子集。若对于R的任意一个可能的关系r，r中不存在两个元组在X上的属性值相等，而在A上的属性值不等，则称X函数确定A或A函数依赖于X，记作X→A，称X为FD左部（left-hand-side，lhs）或者决定项，A为FD的右部（right-hand-side，rhs）或者依赖项。

例1 表1为部分美国医院信息表，包含5个属性ProviderNumber、HospitalName、County‐Name、MeasureCode、MeasureName，分别表示编号、医院名称、城市名称、诊断代码和诊断名称。该表中存在2条函数依赖，Measure‐Code→MeasureName和ProviderNumber→Hos‐pitalName。其中MeasureCode→MeasureName表示诊断代码可以唯一确定诊断名称，换言之，MeasureCode取值相同的元组，其Measure‐Name的取值也相同。如表1中所示，t1［Mea‐sureCode］=t7［MeasureCode］=pn-5c，t1［Mea‐sureName］=t7［MeasureName］=pxeumoxia。

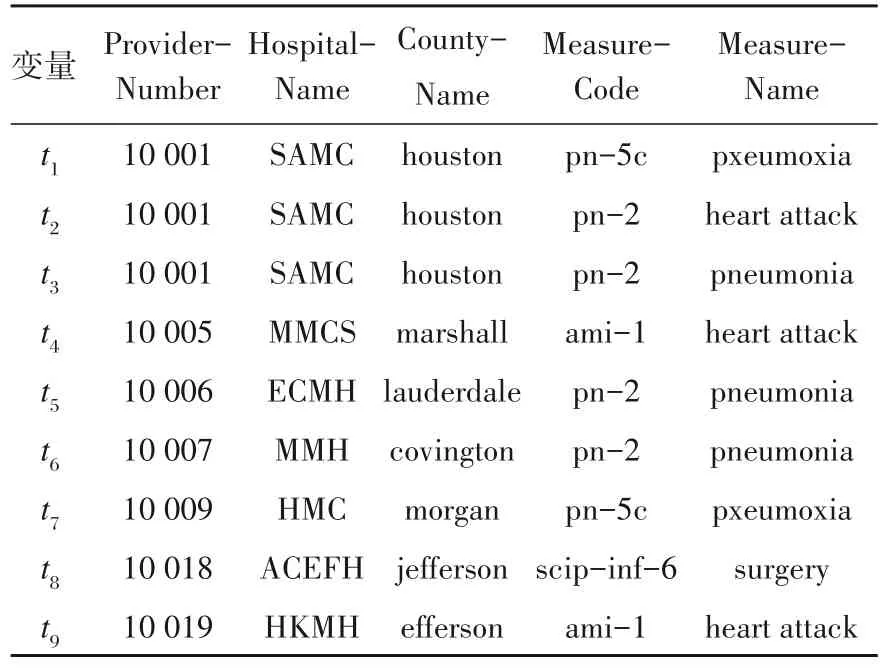
表1 部分美国医院信息表

对于一条函数依赖X→A，若X⊂Y，则称X→A是Y→A的泛化，Y→A是X→A的细化；若X→A的任意泛化在数据集中都不成立，则称其为最小函数依赖；若A∉X，则称该函数依赖是非平凡的。精确的函数依赖挖掘方法旨在挖掘出所有非平凡的最小函数依赖，这就意味着数据中不允许出现任何违反函数依赖的元组。然而，真实数据集往往不是干净的，存在一些数据错误或缺失值，导致原本成立的函数依赖不再成立。为了不丢失任何可能正确的函数依赖，对函数依赖成立的条件进行松弛，允许一定比例的违反，将松弛后的函数依赖称为近似函数依赖。下面从概率的角度给出近似函数依赖的形式化定义。

定义2 近似函数依赖（Approximate Func‐tinal Dependency，AFD）：给定关系模式R，令R上每个属性A的值域为V(A)，则属性集合X={A1，A2，…，Ak}⊆R对应的值域V(X)=V(A1)×V(A2)×…×V(Ak)，假设R中的每个实例D都有一个概率密度fR(D)，这些概率密度形成有效的概率分布PR。给定分布PR及FD：X→A，若存在函数ϕ：V(X)→V(A)，使得下面公式（1）成立，则称X→A为近似函数依赖，其中X⊆R，A∈R，ε是一个很小的常数。

当a=ϕ(x)，特别地，当ε=0时，X→A为函数依赖。可以看出，近似函数依赖通过引入误差ε放宽了函数依赖成立的条件，允许数据中存在一些违反函数依赖的元组。

例2 表1中的一条真实的函数依赖为MeasureCode→MeasureName。当数据发生错误时，t2元组的MeasureCode值由ami-1变为pn-2，此时，t2、t3、t5、t6的MeasureCode值都为pn-2，但t3、t5、t6的MeasureName为pneumonia，而t2的MeasureName为heart attack，导致Mea‐sureCode→MeasureName这条函数依赖不再成立。令误差ε=0.25，则PR（MeasureName=pneu‐monia|MeasureCode=pn2）=0.75，此时可以认为在表1的数据集中函数依赖Measure‐Code→MeasureName近似成立。

现有的近似函数依赖挖掘的方法通常利用样本实例D中(X，A)的共现计数与X值的计数比值作为PR（A|X）的估计，即count（X，A）/count（X）。然而，在给定的样本中，随着X中属性数量的增加，该比值有可能接近1，进而满足公式（1），此时挖掘出的函数依赖是过拟合的。例如，Country Name，Measure Code，Measure Name→HosptialName就是过拟合的近似函数依赖，因为左部属性数量较多，导致每种左部属性取值的计数都为1，左部属性与右部属性共现的计数也为1，从而比值为1。因此，在确定每个右部属性的左部决定集时，应尽量缩小左部属性范围，防止过拟合，提高挖掘的准确率。

1.2 马尔科夫毯

本节首先介绍马尔科夫毯，然后分析马尔科夫毯独立性与函数依赖之间的关系。

定义3 马尔科夫毯［12-13］：指在随机变量的全集U中，对于给定的变量X∈U和变量集MB⊆U，(X∉MB)，属性之间若存在X⊥{UMB-{X}}|MB（⊥：独立），则称满足上述条件的最小变量集MB为X的马尔科夫毯。具体而言，当全集U是贝叶斯网络的各个结点时，节点X的马尔科夫毯是由该节点的父节点Pa(X)、子节点Ch(X)和配偶节点Sp(X)组成，即MB(X)=Pa(X)∪Ch(X)∪Sp(X)。这种定义方式将马尔科夫毯与节点的独立性以及节点间的函数依赖关系联系在一起。

例3 图1是一个贝叶斯网络，节点X5的父节点Pa(X5)={X2、X3}，子节点为Cha(X5)={X8}，配偶节点为Sp(X5)={X6}，因此，MB(X5)={X2，X3，X6，X8}。

图1 马尔科夫毯示意图

根据马尔科夫毯条件独立性的原理，可以得出影响一个变量取值分布的变量都在其马尔科夫毯中。基于这一原理，做出如下猜想：对于函数依赖X→A中的右部属性A，既然X的取值能够唯一确定A的取值，那么X应该在A的马尔科夫毯中。经过引理1的证实，这一猜想得到了验证。

引理1给定属性集U上的关系模式R，对于U中任意属性A，假设其有唯一的左部决定集X，即存在函数依赖X→A，则X一定在A的马尔科夫毯中，即X⊆MB(A)。

证明：采用反证法，假设X不在A的马尔科夫毯中，根据函数依赖X→A可知，X值可以确定唯一的A值。假设X=xi时，对应的A=ai，即P(A=ai|X=xi)=1，因此P(A=ai|MB(A)，X=xi)=1。换言之，当给定X=xi时，A一定为ai，与MB(A)中的属性取值无关，与马尔科夫毯条件独立性相违背，假设不成立，因此X一定在A的马尔科夫毯中。

经过引理1的验证，可以得知，对于每个函数依赖中的右部属性，可以在其马尔科夫毯中搜索左部的决定集，从而避免了在全部属性空间中的搜索。这种优化不仅提高了搜索效率，同时也能有效解决过拟合问题。

1.3 问题定义

给定噪声数据集关系模式R及其概率分布PR，噪声数据集D'和错误阈值ε，挖掘PR的最小且非平凡的近似函数依赖如式（2）所示

式中：X⊆R，A∈R。对于PR采样中的任意一对元组ti、tj，当左部属性集X的取值相同时，右部A的取值也相同的概率是1-ε（ε的值很小）。

2 MB_AFD算法概述

为了解决近似函数依赖挖掘算法的准确率低及过拟合问题，本文提出了基于马尔科夫毯的近似函数依赖挖掘算法MB_AFD。输入为噪声数据集D'以及最大错误阈值emax，输出为每个属性对应的最小近似函数依赖集AFDs，算法MB_AFD的工作内容分为以下3个部分，如图2所示。

图2 算法MB_AFD总体框架图

（1）构建每个属性的马尔科夫毯

对于输入的噪声数据集D'进行采样，训练其贝叶斯网络结构，为每个节点属性构建马尔科夫毯Attribute_MB。

（2）锁定搜索空间的峰值

对数据集中的每个属性，生成其左部决定集的搜索空间，其中每个属性的搜索空间searchSpace可以表示为一个幂集格。接下来，利用每个属性的马尔科夫毯Attribute_MB，在搜索空间中锁定顶峰Peak，从而剪枝去掉大部分的搜索空间，减少搜索的复杂性。

（3）向下泛化搜索

在锁定每个属性搜索空间的顶峰节点Peak后，采用向下泛化验证的策略。具体而言，根据包含的所有子集逐步减少左部候选项的属性个数，从而降低搜索幂级格中的级别。在验证过程中，计算节点的实际误差e，并与预先设定的最大错误阈值emax进行比较，直到找出最小的左部属性候选集。最后，MB_AFD采用分治策略遍历其他属性的搜索空间，依次发现每个属性的最小近似函数依赖。通过这种方式，在搜索过程中可以高效地减少搜索空间，从而提高搜索效率并找到最小的近似函数依赖。

3 MB_AFD算法的搜索策略

本节介绍一种基于马尔科夫毯的近似函数依赖挖掘算法，其基本思想是通过构建贝叶斯网络来生成每个属性的马尔科夫毯，然后利用每个属性的马尔科夫毯来锁定该属性所在搜索空间的峰值。最后，采用向下泛化的方式不断挖掘最小的近似函数依赖。

3.1 构建每个属性的马尔科夫毯

对于给定的噪声数据集D'，每个属性的左部决定项的候选空间包含了数据集中其他属性所有可能的组合，需要逐一对这些组合进行验证，确保其精确误差小于错误阈值。然而，这样的计算复杂度会随着数据集中属性的数量和元组数量的增加而增大，导致求解过程缓慢，并可能生成大量的过拟合近似函数依赖AFDs，从而降低实验结果的精确性。为了解决这个问题，本文提出利用给定的噪声数据集训练数据集中各个属性马尔科夫毯的方法。通过构建每个属性的马尔科夫毯，可以将无关属性排除在左部决定项的候选空间之外，同时删除包含无关属性的集合，从而减小左部决定项的候选空间，并提高挖掘算法的精确率，避免近似函数依赖过拟合。这个方法作为MB_AFD算法的初始步骤，根据定义3依次构建出每个属性的马尔科夫毯，如算法1所示。

算法1：创建属性的马尔科夫毯算法（Create_MB）输入：关系模式R上的噪声数据集D'；输出：每个属性的马尔科夫毯Attribute_MB ；1.V ←数据集D'中的属性；2.θ←结构参数的最大似然估计；3.oldScore←f（skeleton，θ，D'）；4.while true do 5.for newSkeleton of adding or reducing or deleting do 6.tempScore ←f（skeleton，θ，D'）；7.if tempScore＞oldScore then 8. skeleton=newSkeleton；9. end；10.end；11.end；12.for each attribute X∈V do 13.MB（X）←search（X，skeleton，Pa（X）∪Ch（X）∪Sp（X））；14.Attribute_MB ←MB（X）；15.end；16.return Attribute_MB；

算法1首先从给定的输入数据集中进行采样，并学习属性之间的依赖关系，从而训练生成贝叶斯网络结构。本文采用了爬山法［14-16］来生成贝叶斯网络结构（第2～11行），该算法通过贪婪选择来判断是否对模型结构进行更新（第6行），目标是要找出评分最高的模型，从初始的无边空网络模型出发开始搜索，随后进入迭代的搜索阶段。用搜索算子对当前模型进行局部修改，得到一系列候选模型，然后计算每个候选模型的评分，并将最优候选模型与当前模型进行比较。若最优候选模型的评分大于当前模型的评分，则将当前模型替换为最优候选模型，继续搜索；否则，停止搜索，并返回当前最优模型。评分函数中的评分高低作为操作（加边、减边、删边）的依据（第5行），生成所需的贝叶斯网络拓扑图，接着再根据拓扑图中每个属性的父节点、子节点以及配偶节点，生成该属性的马尔科夫毯（第12～15行）。

3.2 向下泛化搜索算法

由函数依赖的定义可知，当挖掘右部属性的决定项时，搜索空间会变得非常庞大，且可能会出现过拟合现象，例如rhs=xi，左部可能是其他剩余属性的组合，即lhs=2Rxi。为了避免这类问题的出现，本文提出向下泛化搜索算法。在每个属性的搜索空间中，从锁定的顶峰向下泛化验证，峰值所包含的所有子集，最终生成最小近似函数依赖。算法的输入包括噪声数据集D'、各个属性的马尔科夫毯Attribute_MB以及错误阈值emax。输出为数据集中存在的最小近似函数依赖集合AFDs，算法2如下所示。

算法2：向下泛化搜索最小近似函数依赖算法（Discovery_AFDs）输入：属性的马尔科夫毯Attribute_MB，错误阈值emax，关系模式R上的噪声数据集D'；输出：挖掘出来的所有最小且非平凡的近似函数依赖AFDs；初始化searchSpaces；初始化PLI ←D'；1.searchSpaces ←UA∈R Create _ AFD_Space（R｛A｝，A，e）；2.for each space _ X ∈searchSpaces do 3. peak ←new priority queue Attribute_MB（X）；4. while peak ≠∅ do 5. P←peek from peak；6. M' ←look up subsets of P；7. if M' ≠ ∅ then 8. remove P from Peak；9. for each H ∈ hitting-set（M'） do 10. if P H is not an （estimated）11. non-dependency then 12. add P H to peak；13. else；14. e ←calculateError（P，X，PLI）；15. if e＜emax do 16. M ←Discovery Generalization（P，

算法2首先根据属性集依次建立搜索空间，并进行遍历（第4～5行）。将该属性的马尔科夫毯确定为顶峰节点peak（第6行），然后根据节点peak剪枝搜索空间，并验证当前节点是否满足实际误差小于给定的误差阈值（第17行），如果满足，则会迭代地逐级向下泛化（第22～36行），目的是找到最小的近似函数依赖；如果当前节点peak及其所有的泛化节点均验证结束，则返回⊥。

引理2 给定属性集U上的关系模式R，假设近似函数依赖X→A在属性集U上验证成立，则Y→A(Y⊆X)可能是最小的近似函数依赖，即A的最小左部决定项则是X的子集。

证明 假设Y→A和X→A在给定属性集U上均成立，并且Y⊆X，可证集合X中的属性个数一定大于等于Y中的属性个数，因此X不是最小的左部决定项。

例3 图3表示属性E在属性集U上的左部决定项候选搜索空间，假设A，C，D→E的实际误差小于给定的错误阈值，则认为A，C，D→E在属性集U上近似成立，但可能不是最小的近似函数依赖。因此，需要减小左部属性集中属性的个数，依次计算A，C→E，A，D→E，C，D→E，A→E，C→E，D→E的实际误差与错误阈值，并进行比较，不断向下泛化来寻找最小的近似函数依赖。

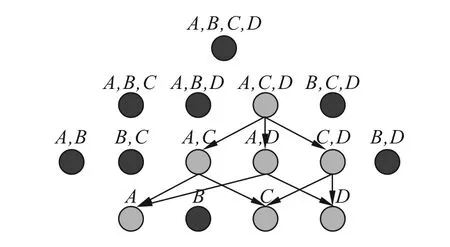
图3 属性E左部决定项的候选搜索空间

引理 3 给定属性集U上的关系模式R，假设近似函数依赖X→A在属性集U上验证成立，则Y→A(X⊆Y)不是最小的近似函数依赖。

证明 假设Y→A和X→A在给定属性集U上均成立，并且X⊆Y，可证集合Y中的属性个数一定大于等于X中的属性个数。因此，Y不是最小的左部决定项。

例4 图4表示属性E在属性集U上的左部决定项候选搜索空间，假设A，C→E的实际误差小于给定的错误阈值，则认为A，C→E在属性集U上近似成立。而A，B，C→E，A，C，D→E，A，B，C，D→E则是过拟合的。因此，搜索空间中的A，C→E的细化形式需要剪枝。

图4 属性E左部决定项的剪枝过程

4 实验测试与结果分析

4.1 实验设置

本节首先介绍了实验环境，接着说明了实验中真实数据集和合成数据集的获取，最后介绍数据集中噪声引入的方法以及F1-score的定义。

算法采用Java实现，实验环境为Intel（R）Core（TM） i5-6300HQ 2.30 GHz的4核处理器；1TB内存；操作系统为Windows10。

真实数据集使用Rayyan、Beers、Flights及Hospital 4个数据集，Rayyan，Beers［Ouzzani et al.，2016］和Flights［Li et al.，2012］是由用户手动收集并清理的数据集，Hospital数据集是常用于数据清洗的基准数据集，其中4个数据集分别包含3、3、4和15条真实的FD，如表2所示。

表2 真实数据集基本信息

合成数据集获取的方法为：给定一个具有n个属性的模式。生成器首先为这些属性分配一个全局顺序，并将有序的属性分成连续的属性集，其大小在2～4之间。设定(X，Y)为这种分割中的属性集，生成器从与域基数设置相关的范围内采样一个值v，并将X中的每个属性分配一个域，以便属性值的笛卡尔积对应于该值，还会将Y的定义域大小赋值为v。在上述过程引入函数依赖，生成了(X，Y)组，其他剩余的属性集执行条件概率分布，生成相关属性集。生成合成数据集的具体设置如表3所示。

表3 合成数据集设置

向已知给定函数依赖的干净合成数据集中引入噪声的具体方法为：将给定的干净数据集中的元组数量标记为n，注入的错误率标记为σ，生成噪声数据的方法为元组t中任意一个属性值t[a]改成t[a']。其中a，a'∈A并且a≠a'，也就是用该属性在数据集中值域的其他取值来替换该值，注入的噪声数据数量为n×σ。在许多案例和研究中，真实数据集的错误率不高于30%，因此本实验中将噪声数据错误率的最大值设置为30%。

用F1-score来评估挖掘近似函数依赖方法的准确性，其中，精确率是指输出的结果中所包含的真实FD条数占所有输出结果的FD条数的比率，记为Precision；召回率是指输出的结果中所包含的真实FD条数占全部真实FD条数的比率，记为Recall；F1-score由准确率和召回率计算得到，定义为

4.2 真实数据实验对比分析

将本文提出的方法标记为MB_AFD，并与以下目前比较流行的最优晶格遍历算法PY‐RO、TANE，模式驱动类算法DFD以及文献［8］提到的数据驱动类算法FDEP进行实验对比。真实数据集中存在自然发生的缺失值错误，为了进行定量分析，需测量出各方法发现的所有近似函数依赖，并与真实的函数依赖进行对比分析。通过表4可以发现其他4种方法的准确率只有2%～3%，造成这种情况的原因是PY‐RO、TANE等方法可以为数据集找到所有语义上成立的函数依赖，通常情况下挖掘出的函数依赖的数量都是成百上千的，与此同时挖掘出来的函数依赖大多都是过拟合或虚假FD，并不是真实存在的。而MB_AFD则根据每个属性的马尔科夫毯缩小左部决定集的候选空间，可以看出MB_AFD很好地删除了无关属性，并剪枝了过多无用的节点，只在马尔科夫毯的顶峰节点的子集中进行向下泛化验证，得到最小的近似函数依赖，从而解决了过拟合的问题。从实验结果来看，MB_AFD的精确率、召回率以及F1-score的值远远高于其他4种方法，对比试验结果如表4所示。

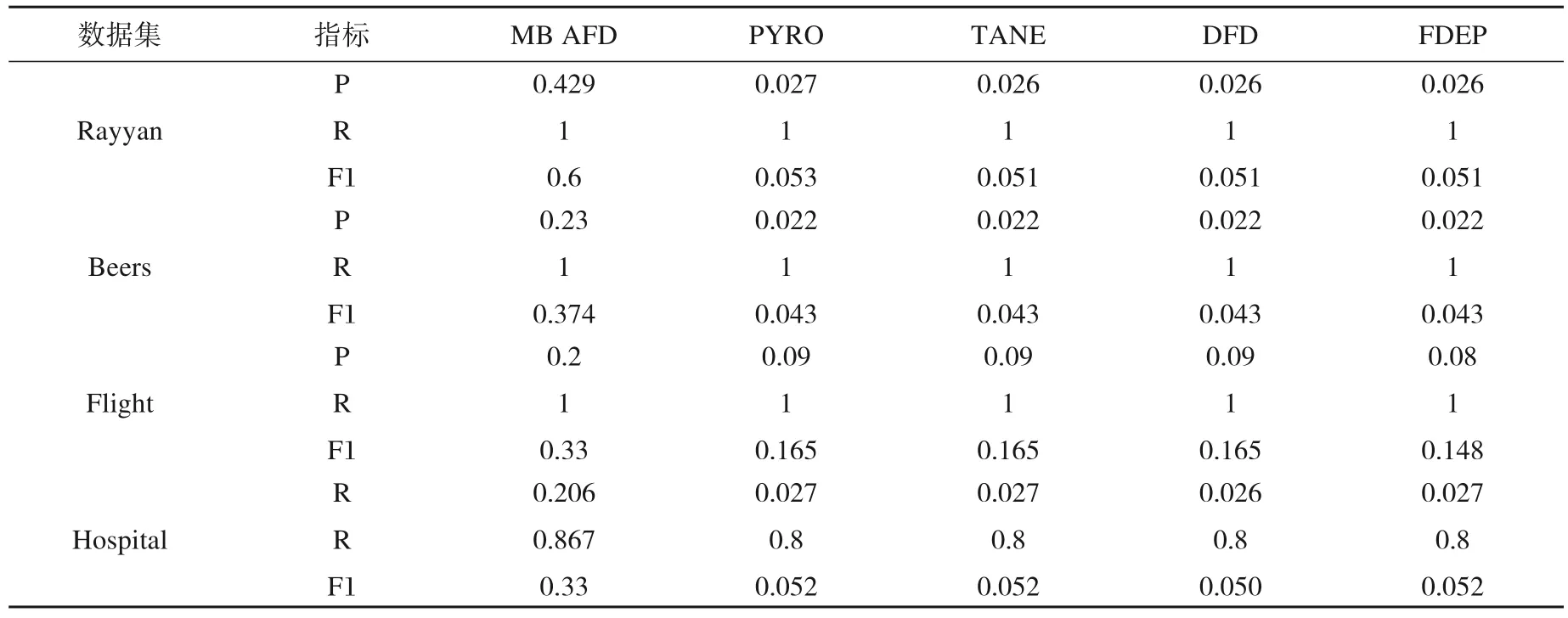
表4 真实数据集的对比实验结果

4.3 合成数据集实验对比分析

为了研究合成数据集中不同因素对近似函数依赖挖掘方法的性能影响，通过改变表3中输入合成数据集的关键因素进行实验探究。

相应的实验结果如图5所示，图5a～5d表明算法在低噪声合成数据集上的F1-score，MB_AFD在不同数据集的得分始终优于其他方法，而且与其他方法相比，MB_AFD受属性数量和元组数量的影响较小，且MB_AFD对于低噪声的数据保持良好的F1-score。PYRO、TANE以及DFD倾向于在合成数据集中生成接近完整的FD图，而不是稀疏的FD图，这使得PYRO、TANE和DFD都具有高召回率，但是精度低、F1-score低。算法FDEP在元组数量很多的情况下，表现出较差的伸缩性，比较元组对的时间过长，不能在短时间内终止程序，测试的结果也是F1-score值低。

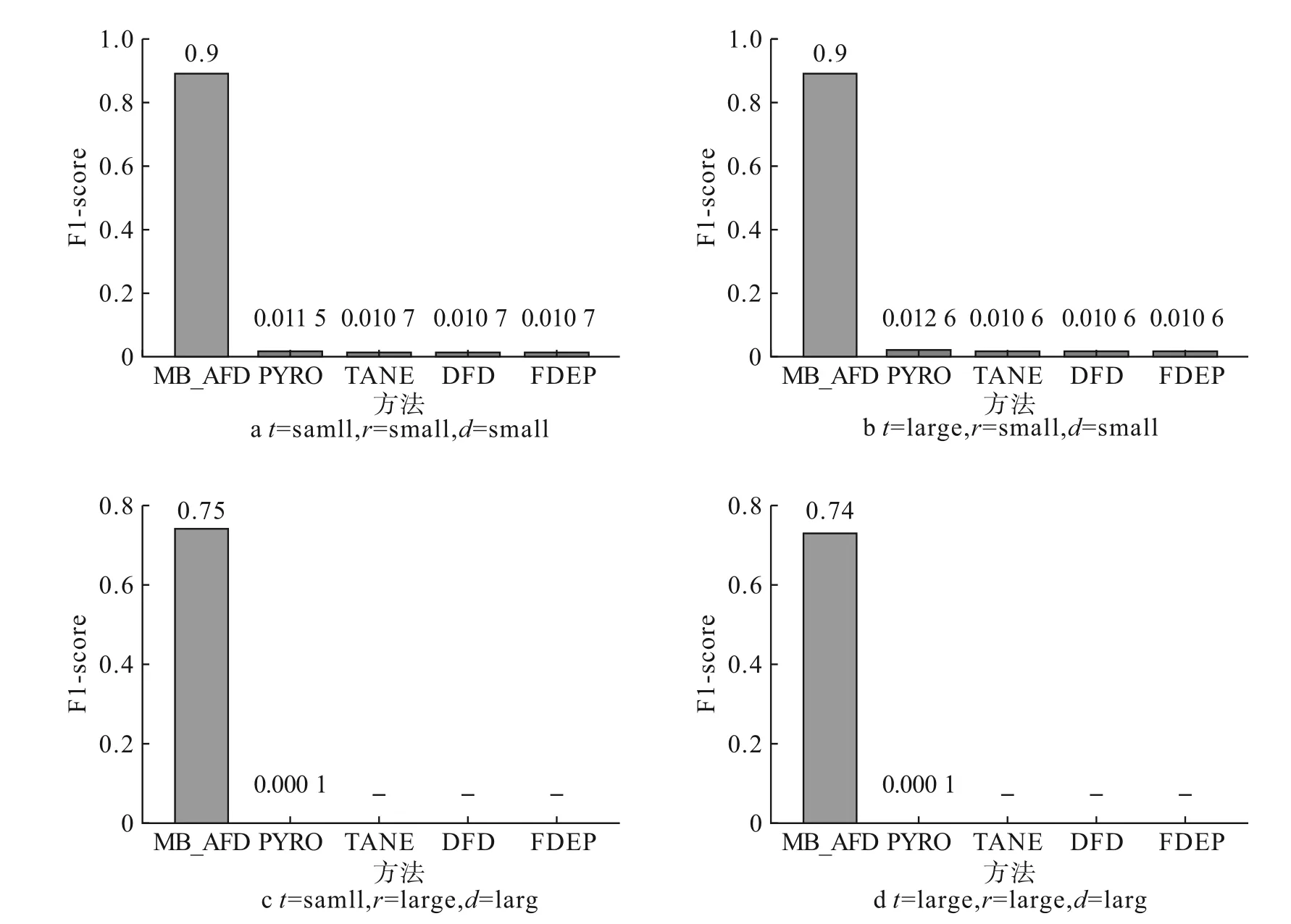
图5 5种方法合成数据的对比实验分析图

4.4 不同噪声对实验的影响

为了对比上述所提及的方法在不同错误率噪声数据集中的准确性，首先通过向给定干净的合成数据集中随机注入错误，人为地在数据集中引入噪声，得到注入错误率从5%到30%均匀变化的噪声数据集；然后分别求解出这5种方法在不同错误率的噪声数据集中挖掘的近似函数依赖结果；最后在同一错误率的噪声数据集中对比每种算法的F1-score。

实验结果如图6所示，通过改变合成数据集中的错误比率进行实验探究，本文提出的MB_AFD方法在每个噪声数据集上都表现很稳定，并未受到数据中的不同错误率的噪声数据影响，F1-score值始终未发生改变，说明MB_AFD对于噪声数据并不敏感。然而，其他4种方法在不同错误率的噪声数据中的F1-score会受到轻微的影响，而且F1-score值也非常低。究其原因，主要是其他4种方法仍保持不断地挖掘语义上成立的近似函数依赖，导致挖掘出的FD数量是庞大的。虽然在不同噪声数据集中挖掘出来的近似函数依赖数量存在变化，但是相比于挖掘出来的近似函数依赖集总体数量还是很微弱的，因而只是有轻微的波动。而MB_AFD的F1-score不但保持不变，而且准确率和召回率也很高，原因是MB_AFD先在噪声数据集上采样并训练贝叶斯网络，生成的马尔科毯并未受到数据中的噪声影响，说明MB_AFD对于噪声数据集有更好的鲁棒性，并允许更低的样本复杂性。因此，MB_AFD在不同错误率的噪声数据中依然可以更准确地发现近似函数依赖。

图6 不同噪声数据集实验结果

综上，本文提出的基于马尔科夫毯的近似函数依赖挖掘算法比当前最优的模式驱动类算法和数据驱动类算法的F1-score更高，并且当数据集中存在噪声时，并未影响MB_AFD的性能。MB_AFD通过创建属性的马尔科夫毯并不断向下泛化验证，不仅缩小了近似函数依赖左部决定集的候选空间，还解决了过拟合问题，使得MB_AFD方法更稳定，精确率和F1-score更高。

5 结论

针对在数据集中挖掘最小函数依赖的问题，本文提出了一种基于马尔科夫毯的近似函数依赖挖掘的算法，通过引入右部属性的马尔科夫毯，锁定左部决定集搜索空间的峰值。通过剪枝左部决定集的搜索空间，解决挖掘近似函数依赖的过拟合问题，同时提出了基于马尔科夫毯挖掘近似函数依赖的框架。实验表明本方法能够高效且高精确率地挖掘出最小的近似函数依赖，同时还适用于错误率不同的噪声数据。