驱动性问题在小学数学项目化学习上的实践探究——结合“简单的周期”谈驱动性问题的设置

江苏省无锡市锡山高级中学实验学校第二小学 夏亚军

驱动性问题是指围绕项目主题，简练而又更易驱动学生参与问题解决的问题。它不仅包含最核心的本质问题，还富含趣味性，更易引发学生的自主探究，是更能促进问题解决的问题。一个好的驱动性问题，有助于引导学生全面地思考问题，设计出解决问题的整体方案。驱动性问题的解决还需关注在解决主问题的过程中不断生成的子问题，及时提炼出有利于形成方法和技能的总结性的子问题来推进学生的项目化学习，促进学生深度参与问题解决的全过程，引发学生的高阶思维。下面，笔者结合“简单的周期”一课的问题设置实践来谈谈如何设计驱动性主问题，并把握其生成的子问题来实施项目化学习。

一、从本质问题和核心素材的分析中设置驱动性主问题

以“简单的周期”一课为例，其本质问题：什么是周期现象？其最核心的素材就是一幅色彩丰富的图画（如图1），意从盆花入手研究，在有了一定的感性认知后，再由学生自主探究、合作交流分析彩灯问题，最后让学生独立自主解决彩旗的问题，通过对比三组素材，引导学生总结提升、回顾反思，从而体会到周期现象，领悟到研究规律问题的一些步骤、方法和技巧。这样的安排思路很清晰，但区分度不高，研究的兴趣激发不够。在实际教学中，由于这幅图画的三维立体感不强，远近的视觉效果不明显，大多数学生会习惯性地由上而下选择素材。这样就很难与教学预设同步，导致教与学的不顺畅。

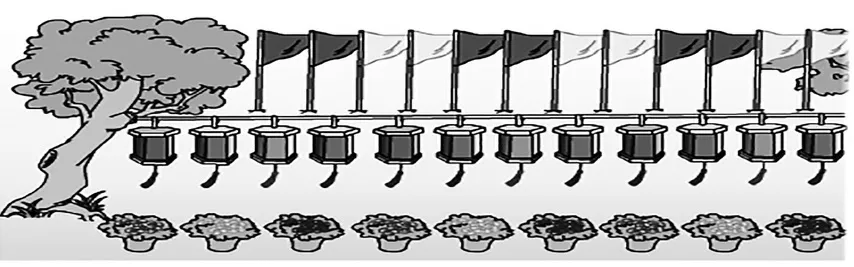
图1

针对核心的本质问题集中但无区分度、问题研究层次感不强和研究素材的顺序难判定这几个问题，笔者创设了以下的真实情境，提出了驱动性主问题。

教师在讲台上用魔术的手法（将已提前撕好的图画放在上面，下面重叠一张白纸）展示，“嘶”的一声（实质撕的是下面重叠的空白纸），学生眼睁睁看着匆忙准备上课资料的教师一不小心撕毁一幅完整的画作。整个教室都静了下来。仅“嘶”的一声，就把学生自然地带入到“真实”情境中。教师不说话，学生也会情不自禁地思考：“老师撕毁了精心准备的画作，接下来该怎么上课呢？我们怎样才能帮到老师呀？”慌乱的教师也嘀咕道：“这可怎么办哦？谁能帮我把这幅画修复完整呀？”

“怎样修复这幅撕毁的画作？”这是个看似与数学无关，却又集中了所有问题于一身的问题。因为要修复这幅画，学生就要去研究残留的画作：它由几个重要部分组成？每一部分有怎样的特征？怎样依据规律接着画？在这些问题的提出、思考和解决中，学生会逐渐清晰“什么是周期现象”，明白“如何运用周期现象解决问题”。“如何修复画作？”这样的问题，不像平常的数学题那样直接和枯燥，它的综合性、趣味性和挑战性也更容易激发学生参与的热情，从而驱动他们积极主动地去寻求解决方案，进行深入的观察和深度的思考，从而体悟出解决问题的一般步骤和方法，获得知识和经验。

驱动性问题藏身于教材的核心素材和本质问题中，教师要加强对它们的分析研究，通过思考和统整，创造性地提出集中度高、趣味性强、富有挑战性的驱动性主问题，驱动学生积极参与、深度思维。

二、在驱动性主问题的解决中关注催生的子问题

思考解决驱动性主问题的过程中会催生出各类子问题，众多子问题的解决是驱动性主问题解决的关键。所以，在问题解决的过程中，教师要注重提出的重点子问题、抓住难点子问题、发现细节子问题，及时抛出具有方法指引性的子问题等，再各个击破，直至问题解决和能力形成。下面，笔者谈谈本课问题设置中的子问题的设计策略。

（一）重点问题分层提：问题分层，拾级而上

要想成功修复画作，学生就会主动、认真地观察、研究已撕毁的残留的画作。通过观察分析，学生会发现这幅残留的画作的精妙之处，它将原本差不多一个层次的问题改造成三个不同层次的问题情境：彩旗的排列中不能确定规律；彩灯排列有规律，但由于紫色灯出现的次数与另外两种灯出现的次数不同，导致规律不易被发现；而盆花图中规律则较清晰明了。通过初步的观察、对比，学生不仅了解了各组图的情况，还甄别出了研究素材的难易程度，从而依据分析和思考把这课的重点问题进行了自主的分层或分类，再进行由浅入深的逐级研究。

在上述过程中，学生在问题解决中再发现问题、编排问题，确定要研究什么，按怎样的顺序来研究。依据实际情况的分析从整体上制订解决方案，有利于大局观的形成，提升从整体上把控事件的意识和能力。教师在重点问题的设计上暗自分层，并引导学生自主分析。战略性的分层研究，给学生的项目化学习创设了阶梯。

（二）难点问题引导提：方法指引，形成技能

从规律最为明显的盆花先展开研究，“这组图形有什么？接着画什么？为什么？如何简单快速地表示出盆花组的排列规律……”一个个引导性的子问题的提出和解决指引着学生体会解决这类问题的小技巧、大方法。如：图案较复杂不易表述时，学生可以选择用汉字、图形、英文缩写等化繁为简的方法来表示；为使规律清晰可见，可以用圈一圈或分一分的方法；当数据较大（如研究第28盆是什么颜色的盆花），列举困难时，可以用除法计算，再依据规律分析来解决问题；当除法计算后弄不清结论时，又能结合画图列举来分析……在问题解决的过程中，学生不断地发现新问题，体验到分类的重要性，感觉到化繁为简的快捷，体悟到数形结合的优越；在不同的方法对比中逐步优化解决问题的方法，形成解决这类问题的一般思路和方法。

盆花组的问题虽然简单，但经过这么多子问题的研究后，学生会形成一套解决这类问题的方法和经验，会自然地应用到彩灯组的研究上。如学生在彩灯组图上圈一圈、分一分或用字母、文字的形式来表示后，就会让彩灯组的规律清晰可见，一目了然。这里及时设计的子问题，指向了规律的发现、表述及应用，引导学生在问题解决的过程中慢慢形成了小技巧、大方法，收获了好经验，提升了解决问题的能力。

解决一个问题时，眼中不能只有这个问题，而是应该心系这一类问题。本课的难点是发现规律，通过一连串引导性子问题的提出和解决，引导学生更加深入和有针对性地思考“遇到什么样的情况时，可以怎样解决”，从而逐步形成解决一类问题的方法和技能，这样的学习会更有效。

（三）巩固问题开放提：开放应用，创造无限

残留的彩旗没出现依次重复出现的规律，没有周期现象，怎么办呢？教师不妨抛出一个开放性的问题：“接着画，可能是什么颜色的？你能当个小小设计师设计并给大家介绍你的想法吗？”这样开放性的子问题能激发学生依据已有的知识和经验，积极主动地展开想象，设计出不同的周期现象。

从找不到周期现象到自己设计周期现象，更加开放的形式引发更深层次的对周期现象的应用，不仅激发了学生设计规律的热情，还给学生提供了无限创造的机会。当学生通过字母、图形或文字等简洁的形式来替换图形，更快、更明了地展示设计时，他们可以充分地展现数学的抽象之美；当学生清晰地用周期现象的知识解释自己的设计时，就能充分地展现对知识的掌握和理解以及综合和应用的能力。

开放性问题是驱动性问题的一个重要形式。开放性问题让枯燥的巩固训练转为开放的自主创造，更能吸引学生的思维积极主动地参与，并使原本只有三组例图的例题内容一下子丰富了起来。更多的周期现象的显现，对于接下来的对比和总结周期现象提供了更多的实践支撑，更有利于学生从感性认识上升到理性的理解。

（四）总结性问题细细提：细节追问，学以致用

虽然我们的综合实践活动课没有课外作业，不需要学生立即去解决相关的数学和实际问题，但周期现象的问题是以后研究许多问题的基础，研究它的过程也是解决许多问题的一般过程。所以，在全课的总结中，教师不能简单地问一句：“今天你有什么收获？”就草草了事，可以通过更多的细节子问题来帮助学生回忆和梳理。如在刚才研究学习的过程中，我们遇到了哪些困难？是如何解决的？

1.寻找规律时，怎样能让规律更清晰可见？（画一画、圈一圈，分组呈现）

2.图案较复杂不易表述时，该怎么办？（用汉字、图形、英文缩写等形式化繁为简）

3.数据较大、列举困难时，如何处理？（用除法计算，再依据周期来分析解决）

4.除法计算后弄不清结论是什么时，怎么办？（结合一个周期图来分析）

5.如果不结合周期图来分析，从除法计算的数据推想到排列的最后一个是什么，你还有什么办法？（有规律，即余数是几，就是这个周期中的第几个，没有余数就是这个周期中的最后一个。）

6.你觉得什么是周期现象？（依次重复出现）

7.生活中还有哪些周期现象？你能利用这些周期现象吗？

在细节追问中，教师让学生再次回顾整个研究过程，在回顾中反思，在反思中提升。这样的细细深入的问，不断地指向知识、方法、技巧和实际问题的问，让学生的思维停不下来，让学生从知识的研究影射到数学的方法和思想上，使整个学习更加深入充实，也为以后的学习研究留下了许多宝贵经验。

巧设驱动性问题，可让学生在主问题的引领下，激发才智，展开宏观的思考与交流，在解决驱动性主问题的过程中注重生成的子问题，让重点子问题可拾级而上，在难点子问题中显现方法、思想，从细节子问题中留下经验，在指引性子问题中生成能力。如此设置驱动性问题，以问题细化研究、深化思维、活化应用、驱动学习，让问题更聚焦、更有趣、更深入，更有利于学生直击问题核心，进入深度思维，促进素养的养成。