“三个理解”视角下的初中数学优化教学设计与思考——以“三角形的边”为例

马卫华

⦿ 江苏省如皋市实验初中

章建跃博士指出:“高水平的教学设计是建立在‘三个理解’上的.”在数学教学中,教师如果能从“理解数学”“理解教学”“理解学生”的角度着手,挖掘数学知识中所凝结的思维活动方式与价值观资源,基于对数学教学目标、方式、规律、特征等的理解制定教学目标,基于对学生心理特点、学习支撑因素等方面的理解设计教学过程,就能让数学教学更好地为学生的学服务,从而让学生更好地理解数学本质,发展数学思维,提升数学素养.现基于“三个理解”的角度对“三角形的边”一课的优化教学设计谈一些自己的思考与观点.

1 “三个理解”视角下“三角形的边”的具体教学设想

1.1 从“理解数学”的角度分析本课的教学内容

理解数学是开展教与学的前提,如果不能真正理解数学,数学教学则只能是“无本之木”[1].理解数学就是深入研究学生的“学”,就本课而言,需要研究“三角形的边”涉及的数学知识背景,需要厘清“三角形的边”这一部分知识对“三角形”整章知识体系的作用与价值,需要明晰本节课应体现哪些数学方法、落实哪些核心素养等.

教材中呈现了一个思考栏目和一个探究栏目,即思考如何将三角形按边、角元素进行分类,在画三角形的实践活动中猜想并验证三角形的三边关系.研究涉及数学知识发展的背景,对于思考栏目,需要有序分类(从边、角元素出发进行归类)三角形知识基础;对于探究栏目,需要先猜想与判定“能否构成三角形”,再运用数学原理及不等变形说理论证“三边关系”.在教学“三角形三边关系”时,可从“两边之和”与“第三边”的大小比较中提出构成三角形的问题,此处可以设计分类讨论的教学活动,即创造性地整合教材中的例1,从等腰三角形的特殊性展开分类讨论.教学中,还可以借助具体实例逐渐推广三角形三边关系的一般性,以渗透从特殊到一般的研究方法.在“能否构成三角形”的探究活动中可以水到渠成地培养直观想象素养和抽象素养;在运用已知的数学原理证明三边关系的活动中可以自然而然地培养推理素养.

1.2 从“理解学生”的角度分析本课的具体学情

学生是教学活动的主体,因此深入研究学生、理解学生是必不可少的环节之一.分析学情并了解学生的认知基础,明确学生学习的困难,从而使后续问题情境的设计更贴合学生的具体实际,且能降低学生学习过程中的困难.此时的学生已经可以灵活辨析三角形的概念,并对三角形的边角元素、三角形的分类、两点间线段最短、不等关系等知识认识深刻,也具备了在实验中发现问题、提出问题、解决问题的学习经验,但应用已知数学原理论证数学命题却是摆在学生面前最现实的困难.

基于以上思考,笔者确立如下教学目标:①在经历三角形三边关系的探索过程中理解性质并学会判断是否能构成三角形;②在体会三角形三边关系的论证过程中,理解并学会自主证明.教学难点:通过“能否构成三角形”的数学体验活动来证明三边关系.

1.3 从“理解教学”的角度分析本课的教学设计

理解教学首先需落实教师的主导地位和学生的主体地位,并在分析学情和教学内容的基础上设计教学活动,搭建学生“学”的桥梁,让学生在积极思考、深入探索、深度合作中习得知识,培养思维,发展素养[2].基于上述理解,笔者设计了如下教学活动:

活动1：整合栏目,思维预热.

问题1小学阶段我们已经与三角形有过亲密接触,那你们认识的三角形是什么样的呢?从自己的理解去说一说.

问题2从“三角形的角”出发,可以将三角形分成几类?从“三角形的边”出发又能分成几类呢?

说明:活动1中的问题让学生在列举三角形种类的基础上,回顾一些本节课所需的基础知识,并调动学生原有知识经验,在经历“有序分类”的过程中体验如何按边、角分类.

活动2：创设情境,温故知新.

问题3试着用自己的话描述“什么是三角形”,并分别说一说图1所示的①②③是否是三角形?

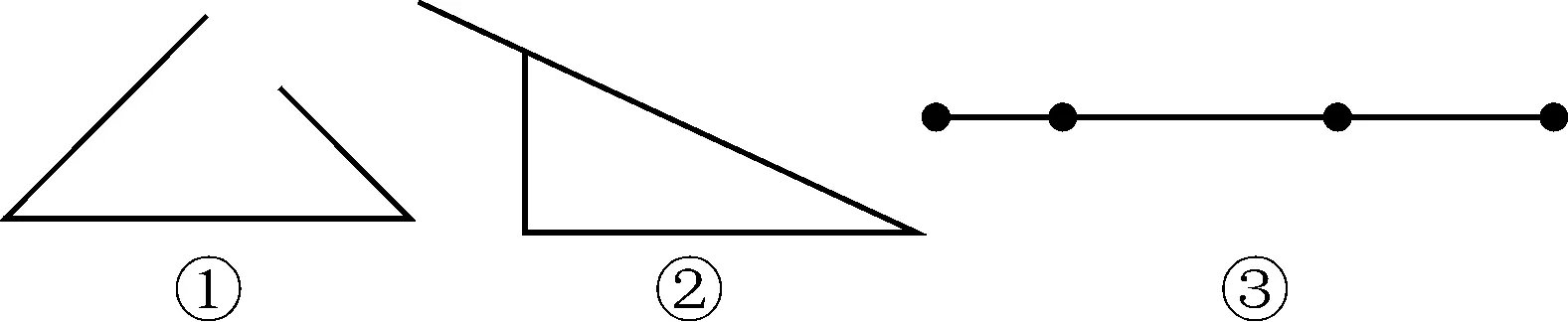
图1

说明:针对学生对“三角形”概念理解不完善的情形来设计问题,让学生在观察和辨析中获得对三角形的深刻认识.同时,这一环节的设计也为后续实验活动的展开提供了知识与经验上的支撑.

活动3：探索猜想,推理论证.

问题4现有3厘米、5厘米、8厘米、9厘米4根小棒,从中选择3根进行拼三角形的实验,并将结果填入表1.观察表1中生成的数据,你能发现什么?其中存在什么数量关系?为什么能构成三角形?

表1

说明：通过选小棒拼三角形的操作实验,学生获得了切实的实验感悟,并在对数据的分析中发现“能否构成三角形”的奥秘,为后续“三角形三边关系”的提炼提供经验支持.

问题5从选择的3根小棒中继续选取2根,对于这2根小棒,从中选取1根并将其剪成两段,再与另外1根小棒一起完成拼三角形的实验,你能拼出三角形吗?

追问:若选取的这2根小棒的长度相同,能拼出一个三角形吗?

问题6通过问题5中的实验,你能发现三角形三边间的数量关系吗?你会证明这个关系吗?

追问:三角形的两边之差与第三边也同样存在某种数量关系吗?

说明：在问题5的剪拼活动中,学生收获了两种不同的实验结果,随之也渗透了分类思想.教师适时的追问引领了“两根小棒之和等于第三根是否可以构成三角形”的探索,让活动探索得以完善.问题6则将教材中的探究栏目推到台前,让学生在深入探索中自然发展演绎推理能力和抽象思维能力.

2 “三个理解”视角下的优化教学设计的实施建议

2.1 以单元整体教学为指引

单元整体教学更有利于知识网络的构建,其整体性特征可以让学生整体把握一个知识体系中所涉及的数学概念关系,从而实现较高层次的知识建构.因此,“三个理解”视角下的数学教学设计需以“单元整体教学”为指引全方位解读教材,如此才能在教学中聚焦数学本质.

2.2 以数学基本活动为途径

数学教学中探究活动始终贯穿其中,这样不仅可以激起学生的学习兴趣,还可以让学生经历概念探究的过程,更能渗透思想方法和落实核心素养.在本节课的教学设计中,通过创设情境引导学生进行思考交流,通过“做数学”的活动引领学生在亲身经历中达成对数学知识的理解性建构,更加深对知识本质、数学思想等的感悟.

2.3 以数学核心素养为目标

教学目标是实施教学活动的起点与归宿,恰当的教学目标是教与学活动顺利开展的重要前提.在数学教学中,渗透思想方法,落实数学核心素养具有十分重要的意义.本节课中,教师基于“三个理解”的角度,以核心素养的落实为目标,站在学生发展的角度,从几何命题活动和落实素养这两条主线展开教学,用核心素养统领整个教学活动,努力增强学生的课堂学习活力,让学生的直观想象、数学抽象、逻辑推理等素养得以落实.

3 结论

总之,“三个理解”视角下的初中数学教学,应当站在理解数学、理解教学、理解学生的视角,以“单元整体教学”为指引,以数学基本活动为途径,以实现数学核心素养培养目标为宗旨[3].因此,我们需要重新审视数学课堂,增强学生的课堂学习活力,落实课改理念,构建“三个理解”视角下的优质数学课堂.