有的放矢微“创”教材,借“题”发挥发展思维——“三角形的中位线”的教学尝试与思考

沈 雯

⦿ 江苏省南京金陵汇文中学

1 问题的提出

新课程理念着重强调,想要促进学生基本技能的形成,需要适度训练且要注重训练的实效性,而非机械重复的实践活动,让学生经历发现和解决问题的过程,在主动参与中不断反思和积累,促进思维的自然生长[1].由此可见,实践性是数学学习的重要特征,需要让学生在“做数学”中主动探究,体验发现乐趣,感悟数学真谛,提高实践与创新能力,发展数学思维,逐步积累有效的数学活动经验[2].

数学实验具备较高的实践性,这也为一线教师的教学设计提供了好的思路与方法,通过整合与再加工实验手册与教材内容,精心设计问题情境与探究活动,用开放性的探究素材引发学生的探究兴趣,用创造性的教学过程为学生提供广阔的探究空间,巧妙地延伸拓展主题,促进学生思维的自然生长.下面以笔者讲授的“三角形的中位线”一课为例,评析微创教材、借题发挥促进思维发展的实践.

2 “三角形的中位线”的教学尝试

2.1 再识旧知,引领新探

问题1我们一起来回顾如何通过折纸得到直角三角形的斜边中线并研究该直线的重要性质,感受折纸的奇妙.仔细观察折痕,你发现了什么?(课件呈现图1.)

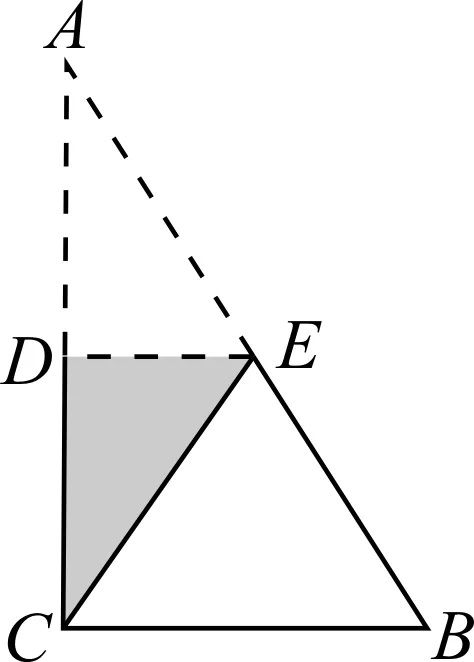
图1

设计意图：温故而知新,回顾折纸与验证的过程,在“再认识”中自然实现认知的“再生长”.在回顾旧知之后,又以开放性问题为导引,引领学生主动探究并发现“连接三角形两边中点的线段是一条特殊线段,它与第三边存在特殊的位置与长度关系”.

问题2观察图形,并阐述三角形中线与中位线的区别.

设计意图：以对比概念的强化方式获得对概念的深入认识与理解.

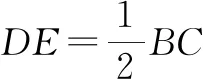
设计意图：问题3中的证明需要猜想与操作的辅助来积累丰富的感性认知,获得如何恰当添加辅助线的灵感,以突破认知难点.也正是有了前面的一系列铺垫,学生才充分感知到“图形的翻折”是演绎推理的重要思路,从而通过“化长为短”的方法完成问题的验证(如图2).

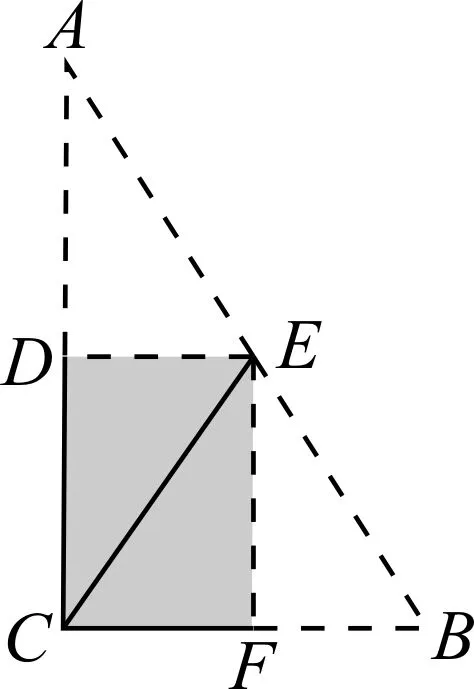
图2

问题4除了“化长为短”的翻折以外,你还能想到其他方法或策略吗?

设计意图：诱导学生在深入思考与探索中生成“补为矩形”的新证法,并利用几何画板的辅助让学生感受图形变化的每一个过程,从而在强化几何直观的同时促进思维的不断进阶.

问题5若这个三角形只是一个任意三角形(非直角三角形),你能折出它的一条中位线吗?请尝试并说出操作过程.

设计意图：学生从中位线定义出发能想到通过折线段中点来折中位线的方法,但很难得出其他折法.教师此时可以鼓励学生合作交流,生成“先折该三角形一边上的高,再折直角三角形中位线”的思路.当然,这个思路不是每个学生都能直观感知的,教师依旧可以借助几何画板进行演示来强化学生的几何直观.

问题6任意三角形的中位线也具有相同特征吗?如何验证?

追问:有没有其他验证方法?

设计意图：以上活动经验所得结论是新活动经验形成的基石,可以促进知识与能力的内化,最终水到渠成地突破难点.学生在多次探索之后形成了方法,并能从“图形旋转”的角度“补短为长”给予证明.

问题7试着简洁概括三角形的中位线定理.

设计意图：在总结提炼的过程中自然而然地训练学生的自主归纳与自主探究精神,并促进学生对知识间联系的顿悟.

2.2 例题巩固,变式提升

例题如图3,DE为△ABC的中位线.

图3

(1)已知DE=5,那么BC的长是多少?

(2)已知∠A=60°,∠B=50°,那么∠AED的度数是多少?

变式1如图4,已知F是BC的中点,那么△ABC的中线AF与中位线DE有何关系?

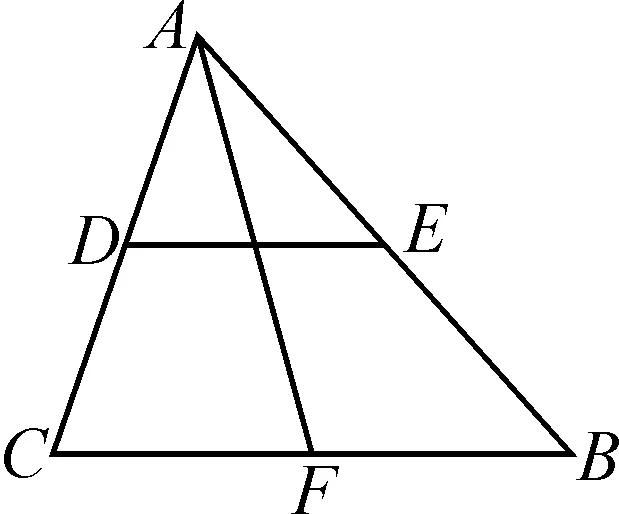
图4

追问:想要AF=DE,则△ABC需满足什么条件?想要AF⊥DE,则△ABC又需满足什么条件?想要AF=DE且AF⊥DE,则△ABC需满足什么条件?

变式2如图5,已知D,E,F分别为△ABC三边的中点,依次连接DE,EF,FD,你有何发现?

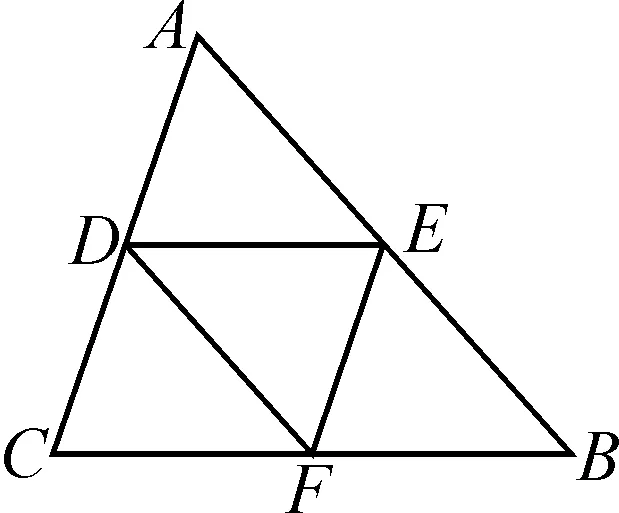
图5

追问:挖掘特殊图形后,你发现了什么?

设计意图：以例题与变式的方式,引领学生沟通知识间联系,发散联想去解决问题,并在解题中不断丰富联想,为后续经验的生长储存充足的能量.

2.3 小结拓展,内化提升

问题8顺次连接三角形的三边中点后得到的三角形为中点三角形,观察这个中点三角形,你发现了什么?

追问1:在研究问题8之后,后续你想研究什么?

追问2:何为中点四边形?你想研究它的哪些方面?

设计意图：此处教师通过“设问+追问”的方式,引领学生用“类比+对比”的方式进行进阶式学习,促进思维的不断生长,实现经验的内化,促进新经验的形成与生长.

问题9回顾本节课的研究历程,分析你收获的经验,并说一说你还想研究哪些内容.

设计意图：通过回顾本节课的探究历程,对学习路径和研究方法等方面有了深刻的感悟,为良好思维品质的形成播下种子.

3 一些思考与感悟

完美融合数学实验与数学教材设计教学,有的放矢地组织教学过程,可以让学生在充分体验中积累丰富的活动经验,在实践运用中内化经验,促进数学思维的自然生长.

3.1 从思维生长点着手,激发学生的源动力

事实上,笔者是做足功课才生成以上教学思路的.在课前笔者生成了多种设计灵感:如从特殊到一般的剪拼活动,后续由于这种设计方案具有一定的普遍性选择舍弃;又如从实际问题情境导入,但由于“概念还应以讲授的方式呈现”而再次选择舍弃;再如以逆向思维的方式导入,即我们可以将三角形纸片剪拼为平行四边形,也可以将平行四边形纸片剪拼成三角形,继而以“拼接线”是三角形的中位线导入,这样的导入方式可以帮助学生积累丰富的活动经验,但无法借题发挥,即无法从三角形中位线这一主题延伸出去,帮助学生更透彻地领悟新知,促进思维的自然生长,因此选择放弃.笔者多次深入思考,决定立足折纸操作与图形的平移、翻折、旋转的已有活动经验,深入整合教学内容,从“利用图形的运动研究三角形中位线”这一主题长驱直下,在磨砺学生实践能力、表达能力和思维能力的同时培养学生的创造力,提高课堂活动的针对性[3].

3.2 借助主题延伸拓展,提高学生的思维力

在数学学习中,学生亲历操作、猜想、验证、证明的过程,获得丰富的数学活动经验,提高数学的思维力.在本课中,教师引导学生“做中学”,亲历操作、实验、观察、思考、交流等活动,拾级而上地感受演绎推理,步步深入地厘清数学本质.这样,在活动的引导下,学生像科学家一样进行研究与探索,自主归纳定义与定理,对研究方法、知识理解有了切实的感悟与思考,能利用已有知识经验大胆猜测与推理,同时在类比与对比中深化了对特殊与一般关系的认识,促进了良好思维品质的深度发展.教学过程中重视主题的强大功能并巧妙延伸拓展,往往可以集反思、运用、巩固和迁移于一身,让学生在获取知识的同时提升数学思维,发展数学核心素养.

在优化教学设计的道路上,教师要善于创造性整合教学内容,通过借“题”发挥引领学生去探索、去感知、去体验,获得丰富的活动经验,提高数学思维力,发展数学核心素养.