“双减”背景下初三高效复习课的实践探索

卢乙玮

⦿ 江苏省张家港市第二中学

初三阶段数学教学内容的显著变化是新知识比例降低,转入全面复习[1],旨在引导学生梳理数学课程知识体系,进而提高解题能力,以更好地应对即将到来的中招考试.作为一种课型,复习课不仅强调数学知识的系统性、整体性,而且有着明确的目的性、功利性,因此即便数学方面的“新知减少”,但学生面临的学习负担“不降反增”.

在“双减”背景下,如何构建初三高效复习课堂、提高学习效率,对数学教师是巨大的挑战.其中,造成复习负担、影响复习效率的问题主要体现在三个方面:首先,初三数学复习课上采取“就题讲题”的方式,缺乏对数学思维过程的关注,即统一标准、按部就班地讲解如何解题,无法满足不同层次学生的需求,不利于学生对所学过的知识进行归纳梳理.其次,初三数学复习课上一味“传授技巧”的行为,导致学生停滞于浅层学习,即学生针对某一个或某一类问题形成认知,却无法深度思考、举一反三,限制了数学知识的融会贯通.再次,初三数学复习课上强调“题海战术”的做法,给学生带来了巨大的负担,教师为了应对中考,收集大量真题、预测题等进行讲解,同时布置大量作业供学生练习,导致学生陷入“低效率复习”的局囿.

1 利用多元表征优化初三数学复习课

宏观上看,初三阶段复习课堂的基本组织形式是“讲解和练习”[2],数学问题是复习活动中的主要对象和承载媒介.而数学问题的设计、要素构成、解答原理等都是依据“数学概念”展开的,在这一前提下,所谓“多元表征”就是利用多种形式、基于多种目的表达出“概念特征”,使之与初三数学复习课上的多元知识点建立联系.但是,传统数学课堂教学活动中,无论“复习课”还是“一般课”,涉及概念教学时多以罗列、解释的方法展开,这样只能满足知识重现的需求,并不能通过“问题表征”来建构知识结构.基于此,可以从数学问题出发,经由数学表征解构,转化成学生便于识别的模式[3],进一步展开解题迁移,这样既可以有效减轻复习负担,也能够提高复习效率.

例如,“相似三角形”(苏教版初中数学八年级下册)复习课上,利用多元表征的实践策略设计,可以通过一组问题展开.

问题(1)请同学们自行画出相似的三角形.

(2)如图1,DE为△ABC上的一条线段,已知DE∥BC,可以推导出角、线段的哪些关系?

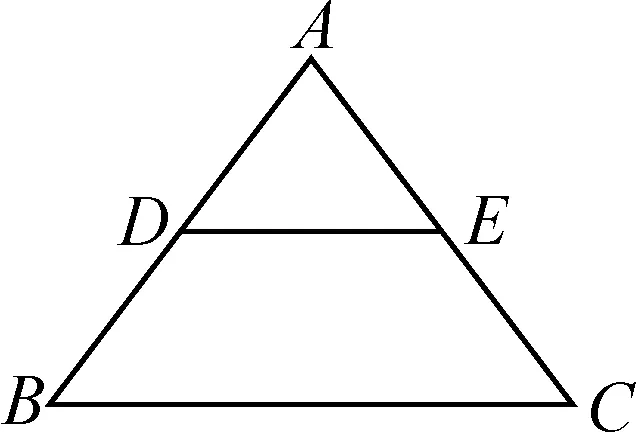
图1

(3)如图2,DE为△ABC上的一条线段,已知DE∥BC,想要使得△ABC∽△AED,需要提供哪些条件?

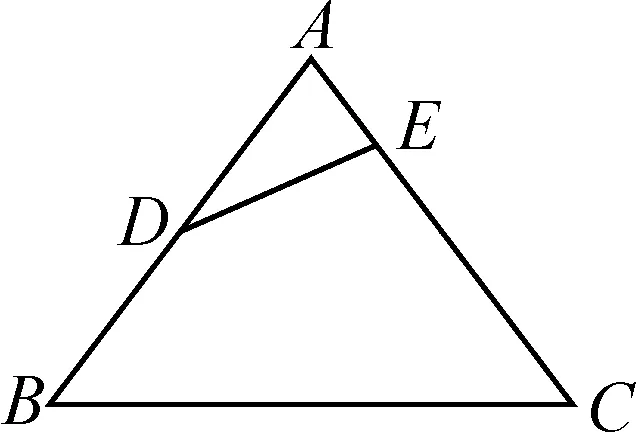
图2

2 利用开放问题优化初三数学复习课

立足“双减”背景,初三阶段的数学复习要着力减轻学生负担,同时要保障复习的高效率、高质量.这一要求在传统初三复习认知中是一对悖论.要达到良好的复习效果,势必要通过大量习题训练、海量知识梳理,因此初三数学复习理应是一项辛苦的工作.为了达成初三数学复习“减负与增效”的平衡,利用开放性问题贯穿初三数学复习课堂是较为科学的方式,这是因为开放性问题更容易引导学生进入深度学习状态,以数学问题为媒介,设置开放性条件、开放性过程、开放性结论等,拓展学生的逻辑思维、形成自我的意义建构,同样能够将不同知识点纳入到同一个体系内,实现融会贯通,举一反三[4].

例如,针对苏教版初中数学八年级上册“相似三角形”的复习,围绕“开放性条件”设计问题,以此检验和增强学生对相关知识点的复习效果.

问题△ABC为任意三角形,D为AB上任意一点,通过添加一个条件,实现两个三角形相似.

本题完全基于“条件开放”设置问题,即没有明确点D的位置,也没有指明哪两个三角形相似,这样就给了学生较大的思考空间.相对应地,采取不同的判定定理,学生得到的答案也是开放的.一方面,如图3,设定点D在AB边上,使得∠ADC=∠ACB,∠BAC为△ABC和△ACD的公共角,因此可以判定△ABC和△ACD相似.另一方面,如图3,过点D作线段DE,使DE∥AC(或DE∥BC),这一条件满足了△ABC和△DBE(或△ADE)相似.通过开放条件的方式,复习课上不需要设置太多问题,但可以同时复习多个知识点,利用已知条件的变化,可以将相似三角形的四个判定定理都列举出来.

图3

3 利用思维导图优化初三数学复习课

从教学实践出发,思维导图在初中数学教学的各个阶段均有运用,尤其在不同课时、单元的复习课上,思维导图呈现了强大的信息整合与知识梳理工具价值[5].进入初三数学复习阶段,利用思维导图优化教学活动能够取得事半功倍的效果.思维导图在初三数学复习课上的应用主要有三种形式,分析如下.

第一,在复习课前段使用,围绕数学概念展开,搭建基础知识结构.每一节复习课确定一个主题,课程前段以梳理概念为主,同时关联数学概念的应用方面及如何运用等.例如,“锐角三角函数”复习课上,利用思维导图将“特殊角度(30°,60°,45°)”“直角三角形边边关系(正弦、余弦、正切)”“数学建模”等分别建立思维导图模块,确保同一层级上的知识点突出共性.

第二,在复习课中段使用,用来解答数学问题,引导学生探寻本质.简单来说,就是将例题的讲解过程用思维导图表示出来,例如:在Rt△ABC中,已知∠B为直角,斜边AC=10,cosA=0.6,求sinA和tanC.将求解的思维过程进行可视化处理,即可生成本题的思维导图,这一过程中明确了何处利用了哪一个知识点.

第三,在复习课后段使用,促进章节内容融合,完善数学知识网络.一节复习课的后段,通常用来总结复习课堂上出现的所有知识点及应用方法,形成一个完整的思维导图(如图4),便于学生课下自主学习.

图4

综上所述,在“减负增效”导向下构建初三数学复习课高效学习模式,首先要摒弃机械性做题、高密度传授的做法;其次是采用科学的手段引导学生,使其能够积极思考、深入学习.如利用“开放问题”的情境,利用思维导图工具、突出问题多元表征等,不仅符合“双减”政策的要求,也能够将碎片化的复习内容聚合成“数学支架”,达成高效率、高质量复习的目的.