聚焦图形本质 合理分类解题——分类讨论思想在求平行四边形顶点坐标问题中的应用

李爱琴

⦿ 南京师范大学附属中学树人学校

1 背景分析

《义务教育数学课程标准(2022年版)》中“图形与坐标”强调数形结合,用代数方法研究几何图形,在平面直角坐标系中用坐标表示图形中点的位置,用坐标法分析和解决实际问题.平行四边形是初中几何中一种非常重要的几何图形,对于它的性质和判定,学生都要会合理应用.与平行四边形相关的问题在中考中也较为普遍,而由于与之相关联的知识点涉及面广,求解方法多、思路活,因此有些学生对这类问题有时束手无策,有时考虑又不全面.

对于初中学生来说,高效而准确的数学解题方法是不可或缺的.在解决有关求平行四边形顶点坐标的问题时,往往要用到分类讨论思想.下面笔者拟通过几例问题分析,谈谈分类讨论思想在求平行四边形顶点坐标问题中的应用.

2 分析说明

如图1,在平行四边形ABCD中,任意连接它的四个顶点中的两个点,可以得到六条线段,分别是线段AB,BC,CD,DA,AC,BD.这六条线段要么是平行四边形的边,要么是平行四边形的对角线.所以,在平面直角坐标系中解决平行四边形问题时,如果已经知道了平行四边形的三个顶点,那么一般分三种情况讨论;而若只知道平行四边形的两个顶点,则一般需要分两种情形来讨论.因为这两个顶点组成的线段只有两种情形,可能是平行四边形的边,也可能是它的对角线.

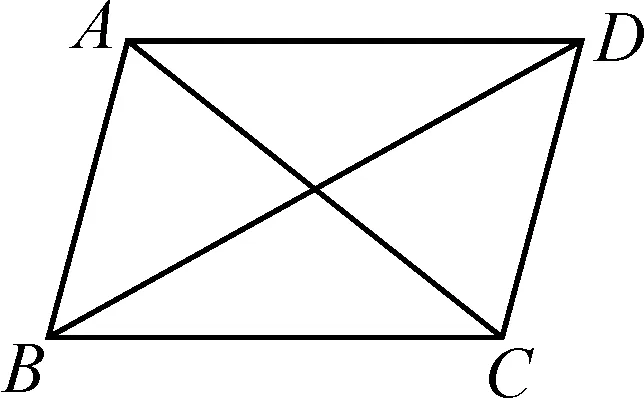
图1

3 案例剖析

案例1若以A(-1,0),B(3,0),C(0,4)为其中三个顶点画平行四边形,求第四个顶点的坐标.

分析：如图2,已知平行四边形三个顶点A,B,C,求第四个顶点,可以分三种情况,分别将AC,AB,BC向右或向上或向左平移就能得到第四个顶点的三种不同位置;也可以分别把AC,AB,BC看成对角线,从而得到第四个顶点的位置.

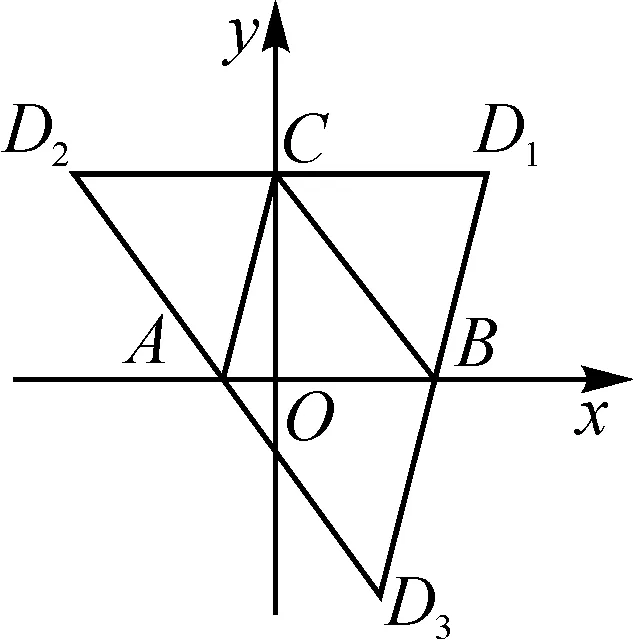
图2

在这里,具体的求解有两种方法:一是运用几何论证方法,根据平行四边形对边平行且相等的性质容易求得第四个顶点的坐标.二是代数论证方法,运用线段中点坐标公式从而确定第四个顶点的坐标.如图2,平行四边形第四个顶点的坐标分别是(4,4),(-4,4),(2,-4).

案例2如图3,在平面直角坐标系中,点A,B的坐标分别为(1,5),(3,3),一次函数y=kx+b的图象与x轴、y轴分别交于点D,C,如果以A,B,C,D为顶点的四边形是平行四边形,则一次函数y=kx+b的关系式为______.

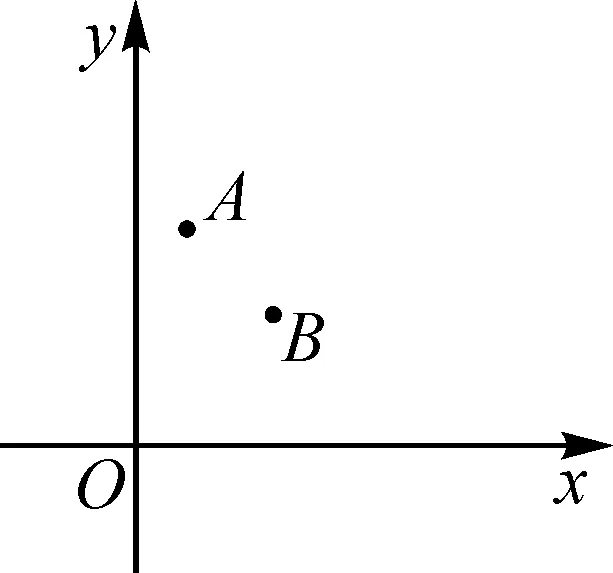
图3

分析：本题只知道平行四边形两个顶点A,B,所以分两种情形,一种是AB为边,另一种是AB为对角线.

先看第一种,如图4,如果AB为边,那么CD也是边,此时过点A作x轴的垂线,过点B作y轴的垂线,两条垂线的交点为E,则根据“平行四边形对边平行且相等”,可得△AEB≌△COD,所以CO=AE=2,EB=OD=2.当点C,D分别在y轴和x轴的正半轴上时,直线CD的解析式为y=-x+2;当点C,D分别在y轴和x轴的负半轴上时,直线CD的解析式为y=-x-2.

再看第二种,如图5,若AB为对角线,则CD也为对角线.平行四边形对角线具有的性质是互相平分,根据线段中点的坐标公式,可以确定AB的中点E的坐标是(2,4).取OD中点F,连接EF,则EF是△COD的中位线.根据中位线的定义及性质可以确定点D(4,0),C(0,8),所以CD所在直线的解析式为y=-2x+8.

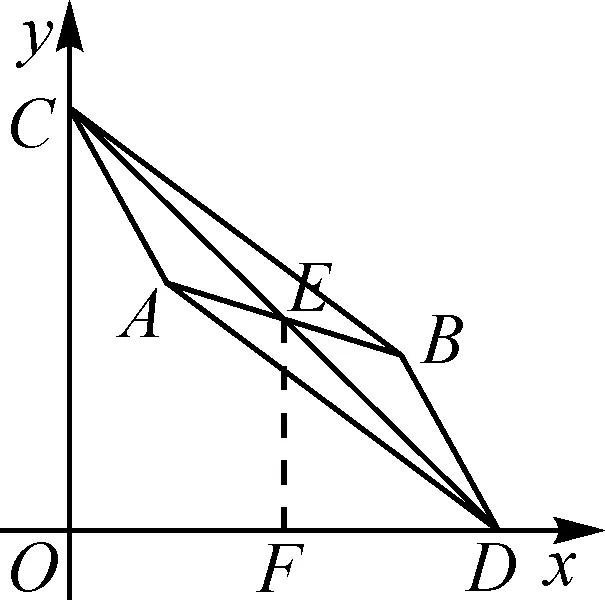
图5

综合上述二种情况,可确定所求的一次函数解析式为y=-x+2或y=-x-2或y=-2x+8.

案例3如图6,在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.

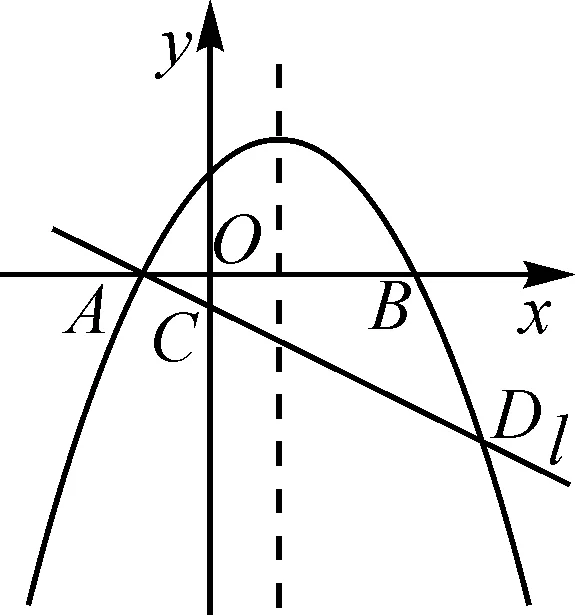
图6

分析：以A,D,P,Q为顶点的四边形是平行四边形,而在这四点中只知道两点A,D,所以分两种情形,即一种是AD为边,另一种是AD为对角线.

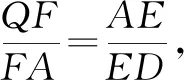
图7

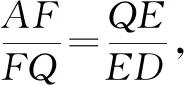
图8

4 解题反思

平行四边形的存在性问题已经成为中考的热点问题之一,教师平时要注意引导学生在遇到这类问题时应仔细分析题目信息,根据已知条件选择合适的分类标准.分类讨论思想是一种比较系统性的思想,有助于解决一般性问题,在数学解题中有广泛的应用.总之,利用分类讨论思想解决有关平行四边形的问题时,一般分三步:第一步寻找分类标准,第二步画图,第三步计算.而难点在于寻找分类标准,如果分类标准恰当,可以使解的个数不重复、不遗漏,从而提高解题的正确率.教师在此类问题的解题教学中,要探索例题的教学价值,教会学生聚焦图形本质,探索分类的合理性、思路的自然化,拓展思维的深度和广度,提高解题能力,使每个学生得到不同的发展[1].