例谈复习课中分类讨论思想的有效渗透<br/>——以“圆”的复习课为例

例谈复习课中分类讨论思想的有效渗透
——以“圆”的复习课为例

2023-11-24陶秋霞

中学数学 2023年22期

关键词：锐角三角等腰三角圆心

陶秋霞

⦿ 江苏省常熟市实验中学

1 在“点与圆”的位置关系中渗透分类讨论思想

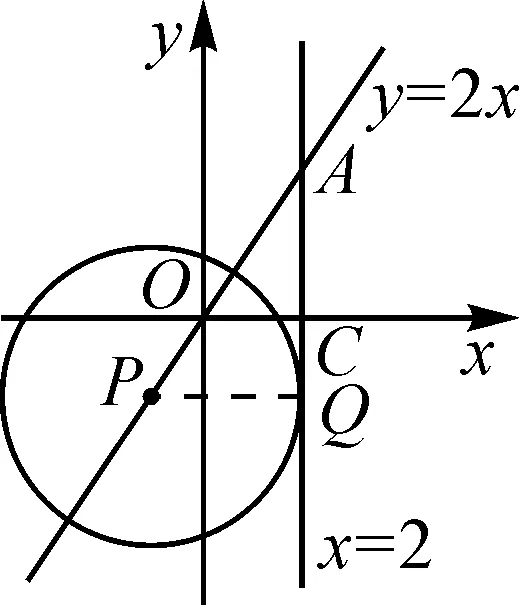
例1若圆O所在的平面内有一点P与圆O上的点的最大距离是m,最小距离是n(m>n),那么圆O的半径是______.

师:在同一平面内,点P与一个圆可能存在哪些位置关系?问题中的点P与圆O可能存在哪些位置关系?为什么?

生:点与圆的位置关系可能有三种——点在圆内,点在圆上,点在圆外.因为题中并没有指明点P在圆的哪个位置,只是点P与圆O同处一个平面,所以点P与圆O也可能存在点P在圆O内、在圆O上、在圆O外三种位置关系.

师:当点P在圆O内部时,如何才能找到点P与圆O上的点的最大距离与最小距离呢?请画出相应的图形.

图1

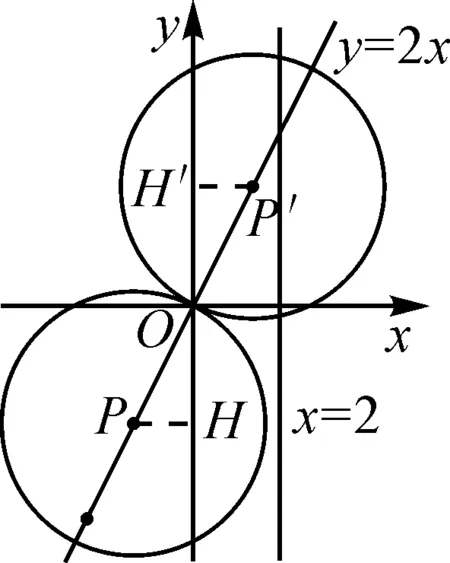
师:当点P在圆O上或圆O外部时,如何才能找到点P与圆O上的点的最大距离与最小距离呢?请画出相应的图形.

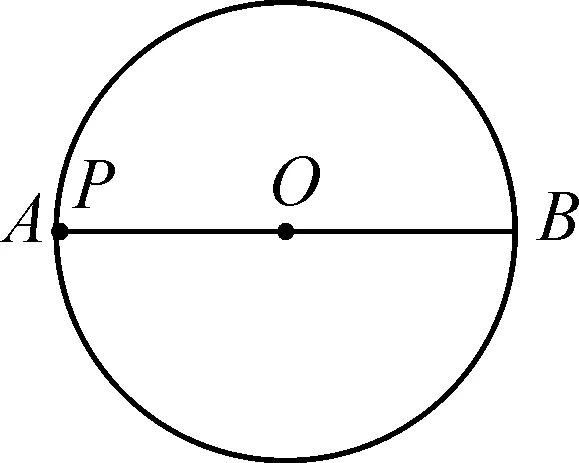
图2

图3

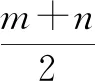
2 在三角形与圆的位置关系中渗透分类讨论思想

例2已知圆O的内接三角形ABC中,AB=AC,圆心O到BC的距离为3 cm,圆O的半径为7 cm,求腰长AB.

师:由已知条件“在△ABC中,AB=AC”,可知△ABC是等腰三角形.对于等腰三角形,可以分为哪几个类型?

生:对于腰与底边不确定的等腰三角形,以三边中的任意一边作底边,会出现三种情况.对于腰与底边确定的等腰三角形,因为内角大小不确定,所以也可能存在三种情况,即等腰锐角三角形、等腰直角三角形、等腰钝角三角形.

师:此题中的等腰三角形ABC可能存在哪些情况呢?为什么?

学生:此题中的等腰三角形ABC可能存在两种情况,即等腰锐角三角形ABC和等腰钝角三角形ABC.因为它属于腰与底边确定,但内角大小不确定的三角形.当△ABC是等腰直角三角形时,圆心在底边上,即圆心到底边BC的距离为0,而题中已知圆心O到BC的距离为3 cm,所以△ABC不可能是等腰直角三角形.

师:请同学们分别画出等腰锐角三角形ABC内接于圆O和等腰钝角三角形ABC内接于圆O的图形,并分别解答.

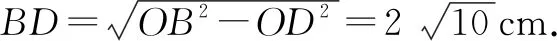
图4

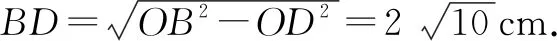
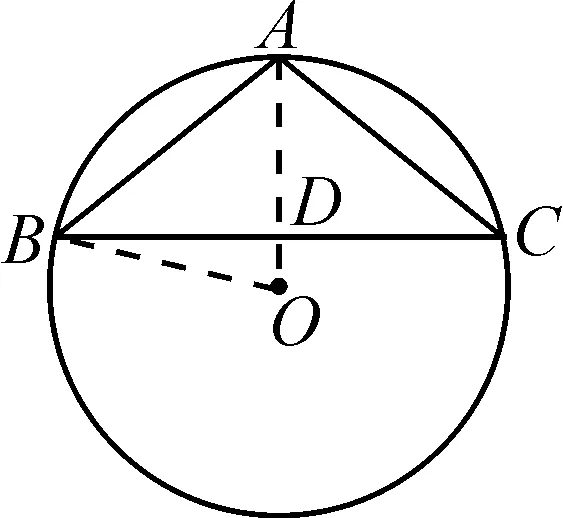
图5

2 在直线与圆的位置关系中渗透分类讨论思想

例2如图6所示,已知P是正比例函数y=2x图象上的一个动点,圆P的半径为3,设点P的坐标为(x,y).(1)当圆P与直线x=2相切时,求点P的坐标;(2)当点O在⊙P上时,求点P的坐标.

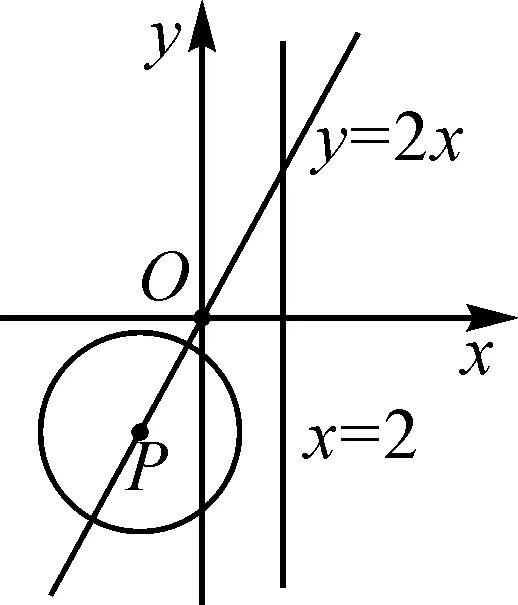
图6

师:认真阅读题目,找出其中的确定条件与不确定条件,并说明理由.

生:正比例函数y=2x的图象是确定的,直线x=2是确定的,因为它们的系数都是确定的.圆P的大小是确定的,因为它的半径为3.圆P的位置是不确定的,因为圆心P是直线y=2x上的一个动点,圆心可以在直线y=2x上自由运动.

师:直线与圆的位置关系有哪几种?有哪些判定方法?

生:直线与圆的位置关系有三种,分别是直线与圆相离、相切、相交.判断直线与圆的位置关系有两种方法.第一种方法,根据直线与圆的公共点个数来判断,当直线与圆有0个、1个、2个公共点时,直线与圆分别相离、相切或相交.第二种方法,根据d与r的关系判定,当d>r,d=r,d

师:当圆P在直线y=2x上从下向上运动时,圆P与直线x=2依次会出现哪些位置关系?

生:当点P从下向上运动时,圆P与直线x=2依次会出现相离、相切、相交,再相切、再相离的位置关系.

师:也就是说,圆P与直线x=2有两次相切的机会,设直线y=2x与直线x=2相交于点A,则分别是圆P在点A下方时和圆P在点A上方时.请同学们分别画出这种相切时的图形,并解答.

生:如图7所示,当圆P在点A的下方与直线x=2相切时,因为直线y=2x与直线x=2相交于点A,则点A的坐标为(2,4),在直角三角形AOC中,tan∠AOC=2.因为圆P与直线x=2相切,若PQ⊥AQ于点Q,所以OC∥PQ,可知∠AOC=∠APQ,则有tan∠AOC=tan∠APQ.因此在直角三角形APQ中,tan∠APQ=AQ∶PQ=2∶1.因为圆P的半径为3,即PQ=3,所以AQ=6,则CQ=2.因为点Q到y轴的距离为2,所以点P的坐标为(-1,-2).

图7

生:如图8所示,当圆P在点A的上方与直线x=2相切时,在三角形APQ与三角形AP′Q′中,PQ=P′Q′=3,∠AQP=∠AQ′P′=90°,且∠PAQ=∠P′AQ′,所以△APQ≌△AP′Q′(AAS),可得AP=AP′,也就是说A是线段PP′的中点.因为点P(-1,-2),点A(2,4),设点P′的坐标为(a,b),根据中点坐标公式,可解得a=5,b=10,所以点P′的坐标为(5,10).