巧妙追问促提升,灵活设计引思考——以“勾股定理”复习课为例

黄建松

⦿ 江苏省如皋市经济技术开发区实验初中

追问是在教师提问的基础上对学生的答案进行进一步的提问,引导学生深入思考,探究问题的本质.问题是教学过程中师生互动的载体,而追问则是有效提升学生思维能力的手段.数学课堂以核心素养为培养目标,旨在促进学生在数学知识、思维方法上的增长,促使学生通过课堂学习建构数学思维,激发学生的数学想象力,形成生长型数学课堂.教师在课堂教学中以追问促使学生深度思考,以逻辑思维的生长贯穿数学课堂,促进课堂教学的智慧生成.

笔者以“勾股定理”复习课为例,以一个三角形为教学起点不断进行追问,促进学生增长知识经验,掌握思想方法,助力思维和综合素养的生长.

1 教学实录

在黑板上画出一个△ABC,如图1,三角形的边AC长度为4,BC边的长度为3.

图1

师:根据这些条件可以得到什么结论呢?

生1:可以得到边AB的长度为5.

(话音未落,马上就有学生抢答.)

生2:AB的长度不一定是5.

师:你们的依据是什么呢?

生1:根据勾股定理,已知AC长度为4,BC的长度为3,可以求出第三边的长度.

生2:勾股定理使用的前提是三角形为直角三角形,但是这道题中没有给出这一条件.

师:看来两位同学的意见不统一,你们觉得哪位同学说得有道理呢?

生(齐):生2说得对.

师追问:很好.那么给这个三角形添加一个什么条件就能使它变成直角三角形呢?

生3:只要让三角形的一个角为90°就可以了,如∠C等于90°,那么AB就是直角三角形的斜边.

生4:应用勾股定理的逆定理,可以添加条件“AB的长度为5”,由此得到AC2+BC2=AB2,所以△ABC是直角三角形.

师:很好!两位同学从不同的角度添加条件,一位是从角的角度,另一位是从边的角度,但都能说明这个三角形是直角三角形.

师:如图2,下面添加条件“∠C为直角”,你能获得哪些结论呢?

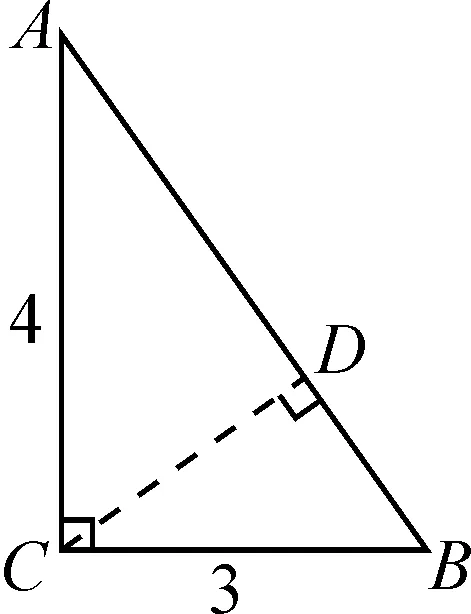
图2

生5:若∠C为直角,则△ABC是直角三角形,根据勾股定理可得AB的长度是5.

师:还可以获得哪些结论呢?

生6:可以求得△ABC的周长和面积.

师追问:不错.还有其他的结论吗?

生7:根据“直角三角形斜边上的中线等于斜边的一半”这个基本定理,可以得到△ABC斜边的中线长为2.5.

师追问:非常好!还有吗?

生8:还能求斜边AB的高.

师追问:怎么求呢?

生9:根据等面积法来求,△ABC的面积等于AC与BC积的一半,也等于AB与对应高的积的一半,所以可以得到CD的长度为2.4.

师进一步追问:现在已经知道了直角三角形斜边上的中线和高的长度,那么还能得到哪些结论呢?请大家先独立思考.

生10:还可计算三个角的角平分线长度.

师:能和大家分享一下你是如何计算的吗?

生10:如图3,具体计算过程略.

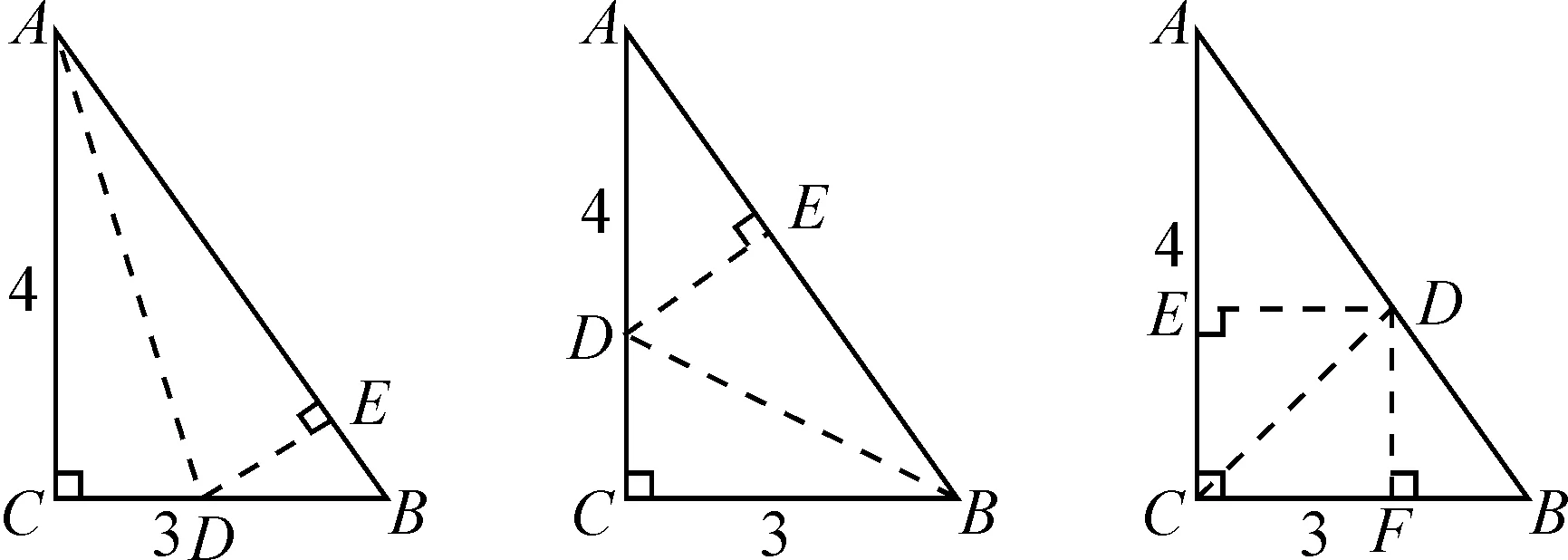
图3

师追问:刚才在计算这三条角平分线时使用了哪些知识?

生11:角平分线的性质定理和勾股定理.

师追问:角平分线与轴对称知识有关,那么你还能联想到其他与轴对称有关的知识吗?

生12:还有线段的垂直平分线.

师追问:如图4,如果添加一条边的垂直平分线,能得到什么结论呢?大家独立思考5分钟.

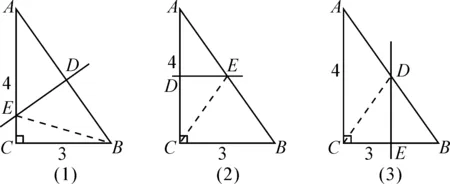
图4

生13:可以求出三角形的两条边与垂直平分线相交所形成的线段DE的长.

图4中的第(2)种情况:若添加AC的垂直平分线DE,则连接CE.根据垂直平分线的性质,可知EA=EC.设AE长为x,此时学生大多想要模仿第(1)种情况用勾股定理求解,但是发现无法很好地表示出三边的长.既然从边的角度不易求解,那么不妨从角出发进行研究,利用EA=EC,得到∠A=∠ACE.由于∠A与∠B的和为90°,∠ACE与∠BCE的和为90°,因此∠B=∠BCE,从而EC=EB,所以EA=EB.显然E是AB的中点,从而可得EA的长度为2.5,进而利用勾股定理求DE的长度.

图4中的第(3)种情况与第(2)种情况类似.

作业:在△ABC中,∠C为直角,AC的长度为4,BC的长度为3,假设动点P从点C出发沿着三角形的边运动,从点C运动到点A再到点B,最后再回到点C停止运动,当△BCP为等腰三角形时,求点P运动路线的长度.

2 教学反思

笔者在教学过程中着力建构勾股定理的知识体系,围绕教学主线,深入探究,形成不断生长的智慧课堂.本课教学过程中贯穿始终的一条主线是如何形成直角三角形,通过直角三角形又可以获得哪些结论.直角三角形属于特殊三角形,因此选择以三角形作为课堂的导入,从三角形开始追问,明确将三角形变成直角三角形一共有两种方法.

接下来建立了另一知识框架,追问有了直角三角形之后,还能得到哪些结论?在教师的追问下,学生的思维不断深入,探索出可以运用“直角三角形斜边上的中线等于斜边的一半”求中线的长度,还能够运用数形结合的思想通过建立方程来求角平分线的长度,等等.

3 教学启示

3.1 以追问促思考,自然生长

在本课中,以连续的追问引导学生深入思考,由浅入深,调动学生运用已学知识思考问题,获得结论,从而使教学环节层层递进,教学活动流畅自然,学生的知识、技能和思维在这样的教学活动中自然得到发展.让学生根据自己已有的知识基础自然生长,既符合学生的认知规律,又体现了数学课堂的精髓.

学生的生长有其自然规律,教师不能为了完成所谓的教学任务,而只注重知识的讲解,忽略学生的思考,导致学生不能真正理解知识,挫伤学生学习的积极性,最终影响学习效果.因此,教师要真正理解学生,深入研究教学,引导学生能够抓住数学的本质,从而实现深层次的理解,使学生能够自然得到生长.

3.2 以追问促探究,提升思维

本课依据学生的答案连续追问,学生根据所学知识很容易求得直角三角形斜边的长以及斜边上的中线长和斜边上的高.这种连续的追问是引导学生进行深层次思考的重要手段,有利于提升学生的思维能力.数学教学不仅要教授学生知识,还要引导学生进行深入的思考,只有深度的课堂才能真正吸引学生,实现教育的价值.教育的目的是为了促进学生思维的发展,只有让思维真正扎根,才能让思维之树枝繁叶茂.

3.3 以追问促设计,全面发展

课前的精心设计是教学活动顺利开展的基础.教师在备课中精心设计追问,充分预设学生在学习过程中可能会出现的问题,使学生的思维力得到提升.

教师在备课时要设想在教师的追问下学生可能会出现的答案,如有的会思考求三角形的周长、面积或者斜边的长,有的会思考斜边的中线,等等.通过追问,引导学生从多个角度进行思考,发展学生的创新思维,培养学生的知识迁移能力,使学生能够举一反三.