开展变式教学,促进深度学习

陈艳阳

⦿ 江苏省南通市北城中学

变式教学以试题改编、一题多解、知识迁移等为手段,从不同的角度引发学生对试题产生新的思考,有效锻炼学生的思维能力,是数学教学中一种常用的训练手段.变式教学使学生对原有的试题产生新的认识,为知识建构、实现举一反三创造了条件,调动学生的高阶思维参与学习活动,有效促进深度学习的开展,提升学习效果.

1 何谓深度学习

深度学习是指学习者围绕学习目标积极主动地运用所学知识进行观察、分析和探究,并主动接受新的知识,领悟其中思想,从而将新知与旧知进行整合,进一步完善知识结构,有效实现知识迁移,寻求解决问题路径的一种学习方式.深度学习要求学习者能够有效整合知识,注重对学习过程的反思与建构,从而培养批判性思维,发展思维的灵活性,提升解决问题的能力.本文从八年级“直角三角形”中的一道习题出发,通过习题变式展开教学,引导学生进行知识和方法的建构与反思,从而实现深度学习.

2 指向深度学习的变式教学

2.1 例题展示与分析

例题如图1,已知AD与BD垂直,AC与BC垂直,AB的中点为E,请问DE与CE是否相等,并说明理由.

图1

解析：因为AB的中点为E,AD与BD垂直,AC与BC垂直,所以根据直角三角形斜边与斜边上中线的关系,可以得到DE,CE都等于AB的一半.因此,DE与CE相等.

本题考查学生对直角三角形斜边与斜边上中线的关系这一知识点的掌握情况,通过将两个直角三角形叠加,找到它们共用的斜边,构建出多种等量关系,实现相互转化,从而找到答案.本题在结构上看似简单,巧妙地构造出共用斜边的直角三角形,实则结构精巧,内涵丰富.通过这道例题,学生更加深刻地掌握了直角三角形的性质定理,提升了知识运用能力.

2.2 变式教学的实践

(1)线段关系

变式1如图2,已知AD与BD垂直,AC与BC垂直,AB的中点为E,CD的中点为F,证明EF与CD垂直.

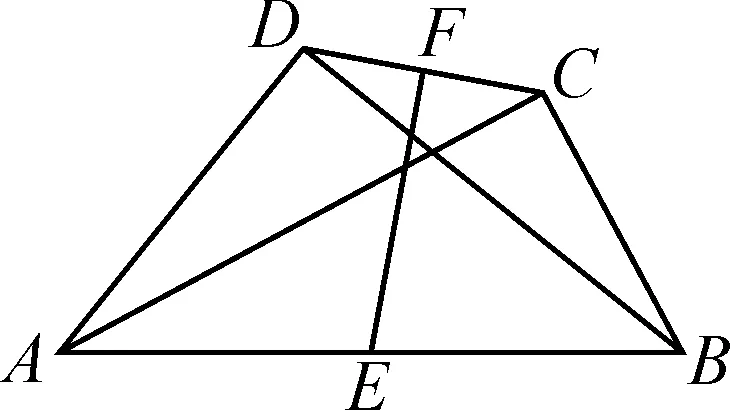
图2

分析：本题从等腰三角形的性质出发,将原题中求解线段的数量关系转化为证明线段的位置关系,从而引导学生能够透过现象抓住本质,运用已学知识构建数学模型,进一步理解三角形的性质定理,灵活运用知识解决问题,发展数学思维能力.

(2)角度关系

变式2如图3,在三角形ABC中,BD与AC垂直,垂足为D,AB与CE垂直,垂足为E,BC的中点为F,∠EFD等于50°,求∠DEF的度数.

图3

变式3如图4,在四边形ABCD中,∠ABC和∠ADC为直角,对角线AC的中点为E,连接BE,ED,BD,若∠BAD等于58°,求∠EBD的度数.

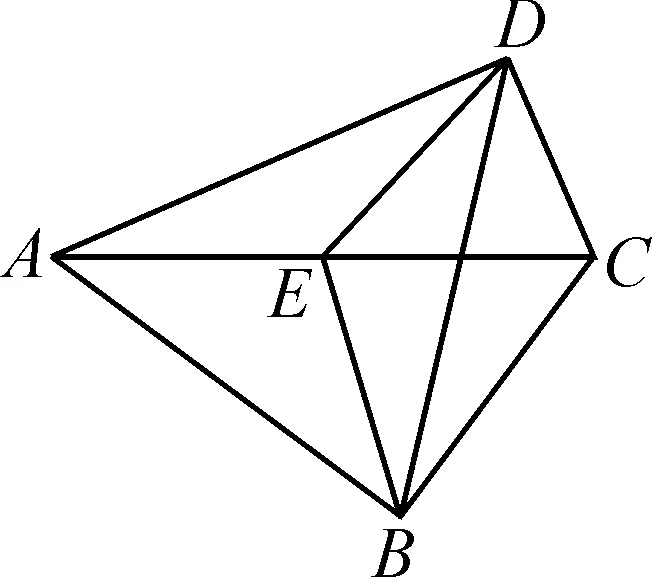
图4

分析：变式2和变式3依托放置在不同位置的直角三角形进行设问,引导学生从不同的角度进行思考,使学生学会知识迁移,从思考线段间的关系转变为思考角间的关系,实现思维的进阶,提升学生综合运用基础知识的能力,进一步理解三角形的性质定理.

变式4如图5,在锐角三角形ABC中,AB与AC上的高分别是CD和BE,M和N分别是线段BC和DE的中点.

图5

(1)连接DM与ME,请问∠A与∠DME之间是什么关系,并证明.

(2)如图6,若将锐角三角形ABC变为钝角三角形ABC,你的结论还成立吗?请说明理由.

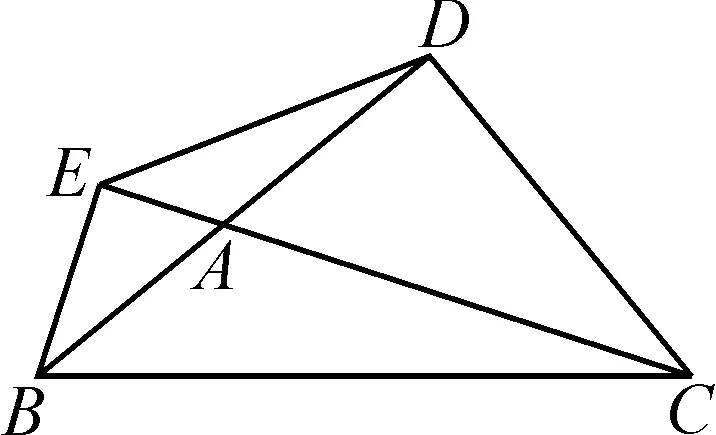
图6

解析：(1)∠DME=180°-2∠A.下面证明.由已知条件,可知BM=DM=EM=CM,因此∠ABC=∠MDB,∠ACB=∠MEC.所以∠BMD+∠CME=180°-2∠ABC+180°-2∠ACB=2∠A,故∠EMD=180°-(∠BMD+∠CME)=180°-2∠A.

(2)连接DM与ME,可以得到∠BME+∠CMD=2(∠ABC+∠ACB),经过转化可以得到∠DME=2∠BAC-180°.

变式4通过条件的拓展,进一步探究三角形中的角度关系,考查学生从复杂问题中抽象数学模型的能力,提升分析和推理能力,进一步促进深度学习.

3 多角度设计指向知识迁移

3.1 基本图形中的线段长度关系

变式5如图7,已知AC与BC垂直,BD与AD垂直,AB的中点为E,AB与CD相交于点F,假设AD与BD相等,EF,DE的长度分别为3和4,求CD的长度.

图7

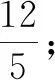
本题利用基本图形中直角三角形共用斜边,运用勾股定理、等面积法、等腰三角形三线合一等知识求解线段的长度,渗透了知识迁移的思想,使学生能够综合运用知识求解问题,培养思维的灵活性.

3.2 基本图形中的坐标问题

变式6如图8,在三角形ABC中,∠A等于67.5°,BC的长度等于4,BE与CA垂直,垂足为E,CF与AB垂直,垂足为F,BC的中点为D.假设以F为原点,以FD所在的直线为x轴构建平面直角坐标系,则点E的横坐标是( ).

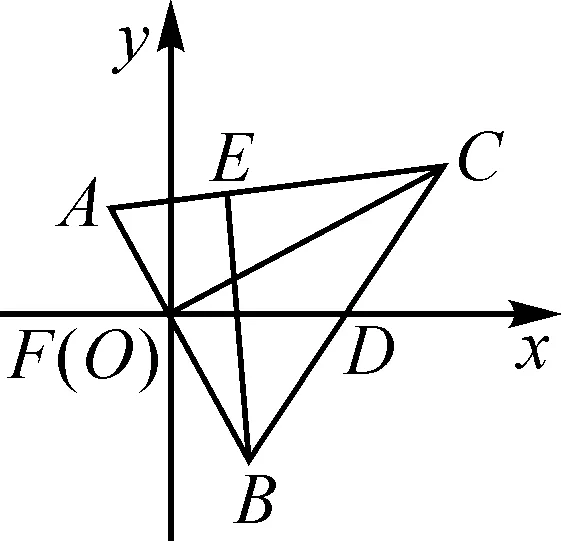
图8

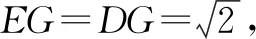
本题在基本图形中加入了坐标轴的知识,使学生学会将三角形的性质、勾股定理、等腰三角形与坐标轴的知识相结合,利用直角三角形共用斜边的知识,结合线段的长度求解点的坐标,进一步发散思维,学会透过现象抓住本质,拓宽了视野,培养举一反三和知识迁移的能力.

3.3 基本图形中的面积关系

变式7如图9,已知三角形ABC中,BD和CE是高,BC边的中点为F,连结DE,EF和DF.

图9

(1)如果∠A等于45°,请判断三角形DEF的形状,并说明理由;

(2)如果∠A与∠DFE的度数比为5∶2,BC的长度为4,求三角形DEF的面积.

解析：(1)三角形DEF是等腰直角三角形.下面证明.因为BD和CE是高,BC边上的中点为F,所以EF等于BC的一半,且与DF相等.因为∠A等于45°,所以∠EBF+∠DCF=180°-45°=135°.因为EF与BF相等,所以∠EBF与∠FEB相等,同理∠DCF与∠FDC相等.于是∠FEB与∠FDC的和为135°,所以∠BFE与∠CFD的和为90°.由此可知,三角形DEF为等腰直角三角形.

(2)作EG垂直于DF,垂足为G.设∠A为5x,则∠DFE为2x,所以∠FEB+∠FDC=∠EBF+∠DCF=180°-5x.因此可得∠BFE+∠CFD=10x,所以10x+2x=180°,解得x=15°.结合BC的长度为4,可以求得三角形DEF的面积为1.

本题涉及等腰三角形的性质和判定、三角形的内角和定理及面积公式,考查学生综合运用知识的能力.通过变式7,进一步考查学生从综合性问题中抽象出基本图形的能力,有效训练学生灵活运用知识和迁移知识的能力.根据这一变式练习,巩固了学生对基础图形性质定理的掌握,同时又开阔了视野,在不同角度的知识应用中实现能力的提升和思维的跨跃.

从基本的习题出发,通过题干条件和设问内容的变化,实现变式练习,使学生能够通过基本的活动经验和数学思想,形成关于基本图形的结论、解题思路和解题方法,并能够将解题方法灵活运用到变式习题中,有效锻炼了抽象思维能力.这样的教学过程能帮助学生建立起一种解决问题的模型,并应用这一模型解决问题,既落实了基本的数学知识和技能,同时又发展了抽象思维能力,在积累活动经验的同时又体验了数学的思想和方法,在变式练习中落实了核心素养.