EAST 反磁剪切qmin ≈ 2 条件下磁流体力学不稳定性及内部输运垒物理实验结果简述*
2023-11-24徐明徐立清赵海林李颖颖钟国强郝保龙马瑞瑞陈伟刘海庆徐国盛胡建生万宝年EAST团队
徐明 徐立清 赵海林 李颖颖 钟国强 郝保龙 马瑞瑞 陈伟 刘海庆 徐国盛胡建生 万宝年 EAST 团队
1) (中国科学院等离子体物理研究所,合肥 230031)
2) (河北省紧凑型聚变重点实验室,廊坊 065001)
3) (新奥科技发展有限公司,廊坊 065001)
4) (核工业西南物理研究院,成都 610041)
托卡马克装置内,建立和维持内部输运垒结构是提高等离子体约束的重要保障.本文简单概述了EAST反磁剪切 qmin ≈2 实验条件下建立和维持内部输运垒的关联物理过程: “离轴锯齿”和双撕裂模不稳定性;快离子激发的阿尔芬波不稳定性;热粒子激发的低频模不稳定性等.首先,“离轴锯齿”是判断实验条件qmin ≤2的重要依据.文中详细介绍了“离轴锯齿”的激发条件、分类方式和先兆模结构等基本特征,其崩塌事件由m/n=2/1 双撕裂模磁重联诱发产生.其次,在“离轴锯齿”振荡期间,快离子很容易激发比压阿尔芬本征模和反剪切阿尔芬本征模.这两类阿尔芬本征模的环向模数为 1 ≤n ≤5,径向位置为环向区域1.98 m ≤R ≤2.07 m (磁轴 R0 ≈1.9 m,归 一化小 半径 0.2 ≤ρ ≤0.45).简述阿尔芬波的激发条件和3 种 不同物理量(热压力梯度、快离子分布函数和环向流速剪切)等之间的关系.第三,在“离轴锯齿”振荡期间,热压力梯度可以诱发低频模不稳定性.利用一般鱼骨模色散关系很容易得出EAST 上低频模的基本特征: 1)离子抗磁漂移频率大小;2)阿尔芬波极化方向;3)反应型动理学气球模特征.低频模不稳定性的激发不依赖快离子,主要发生在高的压力梯度区 α ∝(1+τ)(1+ηi),τ=Te/Ti,ηi=Lni/LTi,也即是足够高的τ和ηi.最后,“离轴锯齿”不稳定性的抑制和内部输运垒结构的建立.EAST 内 qmin ≈2 条件下内部输运垒建立过程中包括3 个重要过程: 1)切向(NBI1L)注入比垂直方向(NBI1R)注入的中性束更容易缓解“离轴锯齿”的爆发周期;2)存在“离轴锯齿”的情况高效缓解微观不稳定性,且此位形更有利于内部输运垒结构的建立;3)内部输运垒建立过程中伴随阿尔芬波(1 ≤n ≤5)不稳定性的激发,内部输运垒维持期间存在热离子温度梯度激发的中尺度微观不稳定性(5 ≤n ≤10)等.因此,理解和掌握“离轴锯齿”实验条件的建立和抑制、阿尔芬波的激发和快离子的再分布、热压力梯度相关不稳定性等物理过程,对于内部输运垒形成机制的理解具有重要的借鉴意义.
1 引言
磁约束聚变装置(包括托卡马克和仿星器),建立和维持内部输运垒(ITBs)结构是提高等离子体约束的重要保障.内部输运垒建立需要几个重要条件[1−3]: 1)径向电场剪切;2)反剪切磁位形;3)qmin大小接近正整数(qmin=1,2,···) 等.最新实验发现,特定的快离子分布函数在内部输运垒建立过程中同样起到了至关重要的作用[4,5].利用电磁模拟GENE 代码的结果发现,快离子的密度梯度分布可以激发一个新的ITBs 结构,被称为快离子引起的反常输运垒(F-ATB)[6].内部输运垒结构最先在JT-60U 装置上发现[7],并相继在TFTR[8−10],DIII-D[11],JET[12,13]C-Mod[14]等装置观察到.一般情况下,ITBs 等离子体常常遭受压力梯度诱发的磁流体力学(MHD)崩塌事件,如发生双撕裂模不稳定性[15].本文将利用EAST 装置qmin≈2 的反剪切磁位形为出发点,系统研究和内部输运垒相关联的各类物理问题.文章的总体布局如下: 第2 部分,总体介绍反磁剪切qmin≈2 条件下相关物理之间的关系图;第3 部分,“离轴锯齿”和双撕裂模的激发条件,分类和先兆模的基本特征;第4 部分,快离子激发阿尔芬本征模不稳定性;第5 部分,热压力梯度激发低频模不稳定;第6 部分,内部输运垒的相关物理过程;第7 部分,结论部分.
2 反磁剪切 qmin ≈2 条件下关联物理
在EAST 托卡马克装置上开展了一系列探索高约束模式放电过程的物理实验.在反磁剪切最小安全因子qmin≈2 的实验条件下,几个重要的物理结果如图1 所示.
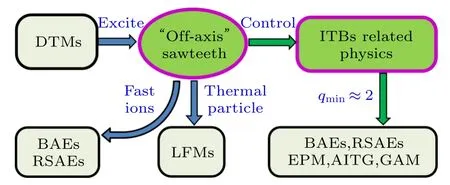
图1 EAST 托卡马克装置反磁剪切 qmin ≤2 条件下双撕裂模(DTM)和离轴锯齿(OAS)、快离子激发低频阿尔芬波(BAEs,RSAEs)、热压力梯度激发低频模(LFMs)和内部输运垒(ITBs)等物理过程之间的相互关系Fig.1.Sketch of different physics phenomena,namely,Double tearing modes (DTM) and “off-axis” sawteeth (OAS),fast ions induced low-frequency Alfvén waves,thermal pressure gradient induced low-frequency mode (LFM) and internal transport barriers (ITBs) under the condition of qmin ≤2in the EAST tokamak.
1)“离轴锯齿”的定义和由来.锯齿的先兆模一般发生在磁轴附近(on-axis),且磁轴处的安全因子满足条件q0<1,而“离轴锯齿”(“off-axs”sawteeth,OAS)的先兆模发生在最小安全因子qmin位置,因此被称为“离轴锯齿”(为了方便,后面去掉了“离轴锯齿”的引号).离轴锯齿的爆发诱因是出现了双撕裂模(double tearing mode,DTM)不稳定性,即周期性地爆发m/n=2/1 双撕裂模,诱发磁重联崩塌事件,这里的m和n分别指极向和环向模数.一般锯齿的先兆模为m/n=1/1 扭曲撕裂模,是与离轴锯齿的先兆模存在本质的不同,具体参考文献 [16].严格意义上来说,离轴锯齿仅仅为周期性崩塌事件.
2)离轴锯齿期间的阿尔芬本征模不稳定性.在离轴锯齿爆发的反磁剪切qmin≤2 的实验条件下,快离子很容易共振激发阿尔芬波不稳定性,例如比压阿尔芬波不稳定性(beta-induced Alfvén eigenmodes,BAEs)、反磁剪切阿尔芬波不稳定性(reversed shear Alfvén eigenmodes,RSAEs)等,具体参考文献 [17,18].
3)离轴锯齿期间的低频模不稳定性及其命名由 来.反磁剪 切qmin≤2 位形下,高温度比τ=Te/Ti≫1 的条件下(Te和Ti分别指电子和离子温度),很容易观察到在离子抗磁漂移频率范围下的一类不稳定性,具有阿尔芬波极化方向的动理气球模特征[18,19].这类模最先被识别为比压阿尔芬声本征模(beta-induced Alfvén acoustic eigenmode,BAAE)[20,21].随后,DIII-D 的实验结果发现,这类不稳定性的激发不依赖于是否存在高能离子[22],且其频率低于BAAE 的带隙中心,是一种与高能量离子激发条件无关的反应型不稳定性,由于其频率小于BAAE 和BAE 等不稳定性而重新命名为低频模(low-frequency modes,LFMs)不稳定性.
4)微观不稳定性的抑制和内部输运垒的建立.在qmin≈2 实验条件下的离轴锯齿振荡期间,通过改变中性束的注入方向等方法,可以有效抑制双撕裂模的爆发周期.当外部注入功率较低时,常伴随电子温度梯度相关联的微观不稳定性的激发和缓解现象;而当外部注入功率超过某一阈值时,等离子体进入具有离子内部输运垒(internal transport barriers,ITBs)结构的高约束模状态.在EAST内ITBs 建立过程中,可观察到丰富的物理现象,如和压力梯度有关的AITG (Alfvén ion temperature gradient)不稳定性,高能离子再分布有关的高能粒子模(EPM)、BAEs 和RSAEs 等不稳定性,等离子体旋转效应有关的GAM (geodesic acoustic modes)不稳定性等.
3 离轴锯齿和双撕裂模
离轴锯齿爆发事件最先在TFTR 装置反磁剪切放电位形中观察到[15].随后,针对双撕裂模的结构和相关特征开展了一系列理论和模拟工作[23−25].快离子可以显著改变双撕裂模的增长率[26],剪切流可以导致双共振面上撕裂模的解耦并抑制双撕裂模的线性增长率[27]等.离轴锯齿和一般锯齿拥有很多类似的地方,如两者均表现出周期性崩塌过程.严格意义来说,离轴锯齿不能称为锯齿,因为它不满足锯齿的基本特征.利用EAST 上观察到的实验结果,我们把离轴锯齿和一般锯齿进行对比,如表1 所列.

表1 EAST 上离轴锯齿和一般锯齿的对比图Table 1.Direct comparison between the OAS with conventional sawteeth in EAST.
1)爆发条件: 离轴锯齿主要发生在反磁剪切位形的实验条件下,存在双有理面如qmin≤2 (q0>2);而一般锯齿发生在单调q分布的条件下,且满足芯部安全因子q0≤1.
2)先兆模结构: 离轴锯齿崩塌前爆发的先兆模为m/n=2/1 撕裂模;而一般锯齿崩塌前的先兆模为m/n=1/1 扭曲撕裂模.
3)先兆模径向位置: 离轴锯齿的先兆模出现在远离磁轴的“环形”区域,对应的径向位置为1.7 m ≤R≤1.8 m (高场侧)和 2 m ≤R≤2.1 m (低场侧);而一般锯齿的先兆模发生 1.8 m ≤R≤2 m (其中磁轴的位置R0≈1.9 m).
4)对等离子体的影响: 离轴锯齿崩塌和一般破裂过程类似,常带来等离子体约束过程的极大破坏作用,如离轴锯齿中心崩塌事件中的电子温度扰动为 ΔTe0/Te0≥30%,等离子体储能下降ΔWdia/Wdia≥10%,并在边界Dα信号上产生极强的热脉冲信号;而一般锯齿芯部的电子温度扰动约为 ΔTe0/Te0≤10%,且崩塌所产生的脉冲不容易传输到边界Dα信号上.主要原因为: 锯齿崩塌过程中同时存在“反转半径”(inversion radius)和“混合半径”(mixing radius),这两个径向位置的存在形成了“护城河”,高效地阻止了粒子和能量的向外输运过程 (“混合半径”的定义见文献 [28,29],主要指锯齿崩塌中粒子和能量输运的最外部区域,锯齿崩塌过程中“反转半径”和“混合半径”处的温度扰动均为 ΔTe/Te≈0,这在3.2 节有进一步介绍).
此外,离轴锯齿和边界局域模(ELM)爆发事件均产生类似的Dα脉冲信号,但两类事件却代表着完全不同的物理过程,如ELM 事件为边界台基区(或外部输运垒)结构崩塌所产生的热量或粒子脉冲信号;而离轴锯齿崩塌为芯部区域双撕裂模发生磁重联过程而产生的热脉冲信号,其传输到边界区域而被Dα信号捕获到.
3.1 离轴锯齿的激发条件
反磁剪切磁位形是建立内部输运垒结构必不可少的实验条件,而qmin≤2 条件下最容易出现的现象是离轴锯齿.因此,探索离轴锯齿的激发条件也是探索反磁剪切出现的实验条件.EAST 上激发离轴锯齿的实验条件如图2 所示.
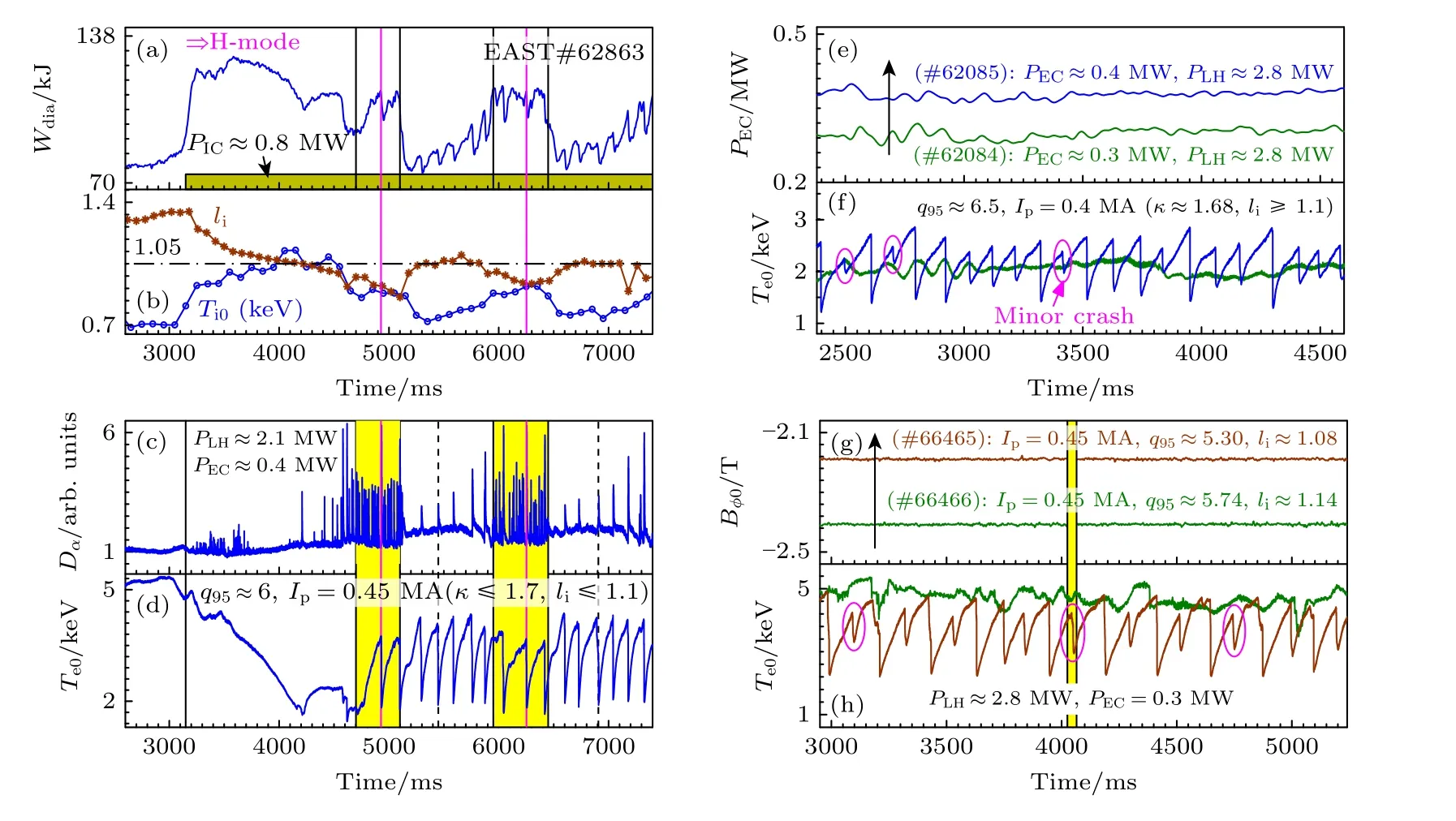
图2 EAST 上离轴锯齿的不同激发条件 (a)—(d) ICRH 辅助条件下离轴锯齿和边界局域模共存现象(#62863);(e),(f) 提高ECRH 功率阈值(#62085) 和(g),(h) 降低环向磁场Bφ实现离轴ECRH 加热(#66465) 条件下激发的离轴锯齿现象Fig.2.Several different conditions for the excitation of OAS: (a)−(d) Coexistence of OAS and ELM instabilities during the ICRH(#62863);(e),(f) effect of ECRH with power threshold (#62085);(g),(h) effect of toroidal field Bφ on the deposition of ECRH(#66465).
首先,离轴锯齿的爆发需要合适的内感li大小.在#62863 中,当离子回旋共振加热(ICRH)系统在t ≈3.15 s 时刻打开,如图2(a)所示,其注入功率为PIC≈0.8 MW.等离子体迅速进入高约束模(H-mode)状态,等离子体芯部的电子密度ne0、等离子体储能Wdia和离子温度Ti0显著增加,并伴随着等离子体内感li的下降.当内感li≤1.05 时,观察到离轴锯齿崩塌事件的爆发,即满足实验条件qmin≤2.在高约束模放电条件下,离轴锯齿崩塌事件和边界局域模(ELM)爆发事件共存,如图2 左列阴影区间所示.需要说明的是,离轴锯齿的崩塌事件对等离子体的约束起到破坏作用,引起等离子体储能Wdia的下降,并容易形成高约束模向低约束模(L-mode)转换.在H-mode 阶段爆发离轴锯齿崩塌事件,引起的Dα脉冲强度远大于ELM事件或L-mode 阶段下离轴锯齿崩塌事件,可能的原因是内破裂诱发了边界输运垒结构的崩塌.从目前实验结果看,ELM 爆发事件对芯部离轴锯齿的影响情况还不太清楚.
其次,离轴锯齿的爆发需要合适的ECRH 功率阈值和注入起始时刻.#62084 和#62085 相邻两炮的放电参数完全类似: 等离子体电流Ip=0.4 MA 完全由LHCD 驱 动(PLH≈2.8 MW),最外磁面的拉长比κ ≈1.68,等离子体内感li≥1.1,95%磁面处的安全因子q95≈6.5.两炮最大的不同为ECRH 的功率大小,当PEC=0.3 MW→0.4 MW时,可以有效地激发离轴锯齿现象,即合适的离轴ECRH 功率可以有效建立实验条件qmin≤2.如图2(e),(f)所示,对比#62084 和#66465 两炮发现,LHCD 和ECRH 功率完全相同(PLH≈2.8 MW和PEC≈0.3 MW).但是,等离子体电流增加Ip=0.4 MA→0.45 MA (q95进一步减小,q=rBφ/RBθ),最外磁面的拉长比下降κ=1.68 → 1.6,这些参数的改变直接影响着li的大小和q剖面的不同,进一步降低ECRH 的功率阈值,并诱发#66465 中爆发离轴锯齿现象.此外,为了更好地修改q剖面,ECRH的注入时刻常常选在电流上升阶段,将在6.3 节中进一步的讨论.
第三,离轴锯齿激发的必要条件—ECRH加热沉积位置远离磁轴,如图2(g),(f)所示.当Bφ·R≈4.16 T·m (如R0=1.9 m 时,Bφ0≈2.2 T),频率为f=140 GHz 的电子回旋共振加热(ECRH)的沉积位置为高场侧 0.4 ≤ρ≤0.5.而当Bφ·R≈4.58 T·m (Bφ0≈2.4 T)时,ECRH 功率主要沉积在磁轴位置,如#66466 炮所示.对 比#66465 和#66466 相邻近两炮发现: LHCD 和ECRH 功率完全相同,等离子体电流均为Ip=0.45 MA,且最外磁面的拉长比也完全相同.但当我们把环向磁场Bφ修改为Bφ0=-2.2T→-2.4 T时(“−”表示磁场和电流方向相反),ECRH 加热的沉积位置由高场侧位置移动到芯部磁轴区域(R=1.66 m →1.89 m),离轴锯齿现象消失.
从EAST 上现有的多炮统计数据来看,单独依靠LHCD 还不能有效建立离轴锯齿周期性崩塌事件,必须借助ECRH 功率的离轴径向位置沉积.图2 中多炮不同放电参数的对比可以发现,激发离轴锯齿(或建立反剪切qmin≤2)的必要条件包括:1) LHCD 的全波电流驱动(平均环电压〈Uφ〉≈0 V);2) ECRH 的共振加热位置,注入起始时刻和功率阈值大小;3) 影响等离子体内感li的多种方式,如额外ICRH 加热,等离子体电流Ip大小,最外磁面拉长比κ,重金属杂质的浓度等.我们把EAST 上2016 年离轴锯齿爆发的参数区间进行统计,可以概括为: 中心线平均电子密度n¯e0≈3×1019m-3,5.3≤q95≤6.8 (0.4 MA≤Ip≤0.45 MA,磁场强度维持不变Bφ0≈2.2 T),LHCD 和ECRH功率之和为 3.2 MW≤PLE≤4.2 MW (PLE=PLH+PEC),最外磁面拉长比 1.6 ≤κ≤1.7 和等离子体内感 1 ≤li≤1.2.详细可参看文献 [16].
3.2 离轴锯齿可以分为三类事件
TFTR 装置[15]最先给出了离轴锯齿的两个不同过程——环形和中心崩塌事件.随后,Tore Supra装置实验结果[30−32]和大量数值模拟计算结果[33−36]进一步演示了这两类事件.近期,双流体模拟结果[37]根据双有理面(这里指双q=2)之间的距离大小和模频率的差异性,把双撕裂模演化过程分为三个参数区间: 1)中心(Central)崩塌区;2)环形(Annular)崩塌区;3)无双撕裂模磁重联崩塌(No-Crash)区域,在EAST 上表征为“广义锯齿”现象.需要说明的是,中心和环形崩塌事件均能产生边界Dα脉冲信号,而“广义锯齿”和常规锯齿相类似,存在“混合半径”,所以未产生Dα脉冲信号.如图3(a)所示,当存在NBI 且满足特定q分布的条件下,离轴锯齿振荡期间交替出现以上三类事件.定义三类事件爆发过程中温度的变化量:ΔTe/Te(t0)=[Te(tc)-Te(t0)]/Te(t0),其中t0和tc分别指崩塌前后的时刻.
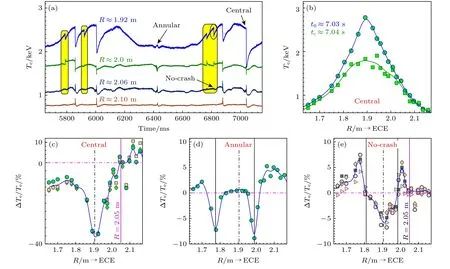
图3 离轴锯齿可以分为中心(Central)、环形(Annular)和“广义锯齿”崩塌事件三大类 (a) 不同径向 Te 信号随时间演化;(b) 中心崩塌事件前后的 Te 剖面的变化;(c)—(e)三类崩塌事件发生前后的温度变化量 ΔTe/Te (磁轴 R0 ≈1.9 m)Fig.3.The OAS can be divided into three categories:Central crash,annular crash and “generalized-sawteeth” crash events.(a)Te for different radial positions;(b) Te -profiles before and after the central crash event;(c)−(e) the relative alterations of ΔTe/Te for the three cases (magnetic axis: R0 ≈1.9 m).
1)中心崩塌事件,如图3(b)和图3(c)所示.双撕裂模磁重联发生在qmin内外两侧的双q=2面之间,当这两个有理面间距较大时或内部有理面靠近磁轴时,崩塌事件直接导致芯部的电子温度或密度快速向外输运过程.在中心崩塌前后,整个芯部区域内的电子温度全部释放出去,和一般破裂过程类似,磁轴附近的电子温度变化量ΔTe0/Te0≥30% (最高可达到 ΔTe0/Te0≈50%).崩塌前后表现出强的高低场侧不对称性,在低场侧可以观察到“反转半径”落在qmin区域2 m ≤R≤2.1 m (这里“反转半径”是借用锯齿的称呼).
2)环形崩塌事件,如图3(d)所示.环形崩塌事件发生的条件为:双q=2 面的间距小于中心崩塌事件或双q=2 面的径向位置远离磁轴区域.因此当发生环形崩塌事件时,内外有理面发生磁重联对芯部电子温度的影响显著下降,芯部电子温度的变化量近似为 ΔTe0/Te0≈0% 或远小于芯部崩塌带来的扰动幅值.在环形崩塌事件发生前后,温度释放最大的区域发生在qmin区域高场侧(1.73 m ≤R≤1.82 m)和 低场 侧(1.95 m ≤R≤2.02 m),温度变化量约为 ΔTe/Te≈10%.
3)无双撕裂模磁重联崩塌或“广义锯齿”事件,如图3(e)所示.当双q=2 面的距离变大或两个有理面上撕裂模频率差异性增加时,双撕裂模的演化进入第3 个阶段.和q=1 面爆发锯齿现象类似,q=2 面附近爆发的“广义锯齿”过程中同样存在“反转半径”和“混合半径”,对应的位置分别在R≈1.99 m (内q=2 面位置)和R≈2.05 m (外q=2面).在“广义锯齿”崩塌前后,由于内q=2 面附近磁岛结构的形成,导致芯部的粒子或能量释放到“反转半径”和“混合半径”组成的环形区域(即双q=2 面之间的区域),而R ≈2.05 m 附近的磁岛结构未发生任何改变,即未发生双撕裂模的磁重联崩塌过程.
在q剖面相似的条件下,经常观察到图2 右列所示的小崩塌事件.这些小崩塌过程的“在轴”(R=1.87 m)和“离轴”(R=1.98 m)区域的温度扰动分别为 ΔTe/Te|(R0≤1.9m)≤10% 和ΔTe/Te|(R=1.98m)≈40%,表现出环形崩塌特征,可参考文献 [16].实验上区分环形崩塌事件的边界条件存在相对性.当不存在快离子的背景条件时,离轴锯齿表现为中心和环形崩塌事件交替出现,如#62085 和#66465 炮所示;而在快离子环境下离轴锯齿常常表征为中心崩塌事件,如#62863 炮所示;而“广义锯齿”出现的条件相对苛刻,偶尔会伴随中心崩塌事件,并常常出现在内部输运垒结构的形成初期.因此,在实验中避免出现环形和中心崩塌事件,并通过改变等离子体旋转或q剖面结构等方式而进入“广义锯齿”的运行区域,对内部输运垒结构的建立具有重要的物理意义.
3.3 先兆模的形成和双撕裂模的激发
理论模拟中关于双撕裂模形成的各种模结构随时间演化过程,在实验中均体现在离轴锯齿的先兆模阶段.因此,分析先兆模演化过程,可以更好地理解双撕裂模的演化进程.选取#66465 炮中具有环形崩塌特征的小破裂事件,该崩塌过程在靠近磁轴位 置R ≈1.87 m 的温度扰动 ΔTe/Te≈15%,而在远离磁轴区域R ≈1.97 m 为 ΔTe/Te≈40%,如图2(h)中的阴影区间所示.这个崩塌前爆发的m/n=2/1 先兆振荡模结构,如图4 所示.需要说明一下,图4(b)为水平SXR 阵列所有的弦线沿着等离子体极向截面上下分布,ρ(Z/a) 代表弦线和磁面切点的归一化径向位置,ρ(Z/a)>0 代表切点位置在赤道平面的上半空间.离轴锯齿崩塌过程可以概括为3 个阶段.

图4 离轴锯齿崩塌前激发m/n=2/1 先兆振荡模(图2 #66465 阴影区间放大结果) (a) 不同径向ECE 信号;(b) SXR 阵列相对扰动信号(δIsx/Isx)沿着Z 方向随时间演化分布图;(c) 边界磁探针频谱图;(d) ECE 阵列相对扰动信号(δTe/Te)沿着R 方向随时间演化分布图.说明: 离轴锯齿崩塌前可以观察到两次不同的崩塌事件(t ≈4.043 s和t ≈4.05 s)Fig.4.The m/n=2/1 precursor mode is taken place before the final collapse of OAS: (a) ECE signals of different radial positions;(b) relative fluctuation of δIsx/Isx for SXR array along Z direction;(c) spectrogram of edge magnetic signal;(d) relative fluctuation of δTe/Te for the ECE array along R direction.Note: two different collapse events are observed successively (t ≈4.043 s and t ≈4.05 s).
首先,发生小破裂事件并引起温度的下降.1)小破裂事件引起芯部温度下降最大的区域,发生在离轴区域R ≈1.97 m,温度下降幅度达到了ΔTe/Te≈14%,而在靠近磁轴的区域R ≈1.94 m温度下降量仅为 ΔTe/Te≈5% (磁轴R0≤1.9 m).对比发现,中心崩塌前也发生类似的小破裂事件,但其引起的温度下降最大的区域发生在磁轴附近.2)磁岛结构的激发是小崩塌事件(t ≈4.043 s)的主要原因.如图4(c)所示,边界磁探针测量到的m/n=2/1 撕裂模频谱信号随着小破裂的出现而同时被激发起来,并同时在SXR 和ECE 信号上观察到密度或温度扰动.
其次,先兆振荡模的空间位置以及极向和环向模数.1)先兆振荡模主要发生在环形区域1.97 m≤R≤2.07 m (低场侧)和 1.7 m ≤R≤1.8 m (高场侧),并在环形区域内形成扭曲模结构(整个区域出现同相位正负变化的温度或密度扰动).2)先兆模的极向结构在SXR 阵列上表现为上下偶对称结构(一个波峰和两个对称的波谷结构),类似也可以在ECE阵列上看到高低场对称的模结构,即m=2.环向模数n=1 很容易被边界磁探针获取,该模式的传播方向沿着电子抗磁漂移方向.当存在快离子时,m/n=2/1 先兆模的传播方向发生改变(沿着离子抗磁漂移方向).
最后,先兆振荡模的演化和双撕裂模结构的形成.1)先兆模的外q=2 面磁岛结构在低场侧2.06 m ≤R≤2.08 m最先被观察到.随着芯部能量或粒子的向外输运,模式振荡频率不断减小(图4(c),f≤2 kHz),并伴随着磁岛宽度的增加和径向位置向内移动,如图4(d)中的品红色圆圈所示.2)先兆模的内q=2 面磁岛结构在低场侧1.94 m ≤R≤1.97 m 可以观察到,表征为正负相位反转面.3)先兆振荡模双磁岛链(主磁岛,2.02 m ≤R≤2.06 m ;次磁岛,1.94 m ≤R≤1.97 m)的形成,即m/n=2/1 双撕裂模发生磁重联过程是导致离轴锯齿崩塌的主要原因,并在崩塌阶段产生强磁扰动信号(图4(c)中高谐频扰动,2 kHz ≤f≤5 kHz).在EAST 离轴锯齿先兆模实验中,通常是外q=2 面的磁岛最先被激发起来,随后才是内q=2 面磁岛.可能原因如下: 由于正剪切效应,外q=2 面附近的磁岛结构优先被激发起来;在qmin区域很容易激发并形成自举电流[38],并抑制了内q=2 面磁岛的激发.
4 高能离子激发阿尔芬本征模不稳定性
比压阿尔芬本征模(BAEs)和离子温度梯度模(ITG)不稳定性之间的关系[39,40],或反剪切阿尔芬本征模(RSAEs)和ITG 不稳定性之间的关系[41],均是内部输运垒(ITBs)物理需要关注的重要方向.BAE 不稳定性的研究最先可追溯到DIII-D 装置[42],其测量完全符合理想MHD 代码GATO 的模拟结果[43].BAE 的频率近似为环形阿尔芬本征模(TAE)频率的一半,且BAE 的本征频率随着等离子体比压的增加而升高.当考虑热离子动理学效应时,如有限拉莫尔半径(FLR)和有限轨道宽度(FOW)效应,阿尔芬连续谱可以分裂成多支离散的本征模结构,即动理学比压阿尔芬本征模(KBAE)[44,45].实验和模拟结果的对比发现[46,47],快离子的比压βh、初始速度v0、轨道宽度ρh等参数对BAEs 不稳定性的激发起到重要的作用,而q剖面的不同又会引起阿尔芬本征模结构的变化.此外,等离子体的磁面拉长效应(或三角形变)会影响BAEs 增长率和本征频率[48,49].具有反磁剪切和ITBs 结构的等离子体运行模式中,常又会伴随一个类似阿尔芬瀑布(ACs)结构的模式,称为RSAEs[50].RSAEs 本征模的一个重要标志为: 频率的起始点为BAE 频率,并在很短的时间尺度内(约100 ms)完成向上扫频,TAE 为向上扫频截止频率点,具体可以参考GYRO 程序模拟结果[51].RSAEs 不稳定性的出现标志着反磁切q剖面的建立,而利用测量RSAEs的频率和模数等参数,可以有效地反推出等离子体背景的参数(如qmin位置和时间演化),这种方法称为MHD 光谱仪[52].对RSAEs 不稳定性已经开展了丰富的理论和实验研究,这里不再详细讨论.
比较幸运的是,在EAST 上离轴锯齿振荡的实验条件(qmin≤2)下,中性束产生的快离子可以同时共振激发BAEs 和RSAEs 这两类不稳定性.如图5 所示,BAEs 和RSAEs 不稳定性被多道的ECE 阵列所捕获到,其径向分布为1.98 m ≤R≤2.07 m (磁轴R0≈1.89 m,归一化小半径为0.2 ≤ρ≤0.45,径向覆盖范围约为 Δr ≈9 cm,Δr/a ≈0.2).模式的中心位置落在R ≈2.025 m,对应着归一化小半径ρ ≈0.3,即为qmin的径向位置.BAEs和RSAEs 的本征频率可以用下面的公式进行表示[44,53]:

图5 BAEs 和RSAEs 的径向位置 1.98 m ≤R ≤2.07 m (归一化小半径 0.2 ≤ρ ≤0.45),qmin 位置为 R ≈2.025 m (ρ ≈0.3)Fig.5.Radial coverage of the pairs of BAEs-RSAEs is located at 1.98 m ≤R ≤2.07 m (the radial position of qmin should be located at R ≈2.025 m).
其中,mi是指(氘)离子的质量,Te和Ti分别为电子和离子温度,vA是 阿尔芬速度,ωBAE是指BAE剪切阿尔芬连续谱极值点(continuum accumulation point,CAP)附近的角频率,Δω是指由于快离子的压力和有限压力梯度等带来的修正效应.
从图5 可以看出,BAEs 和RSAEs 两种不稳定性均存在至少4 支不同环向模数n(或极向模数m)阿尔芬本征结构.在等离子体坐标系下,不同环向模数的BAEs 频率或RSAEs 向上扫频的初始频率是相同的.在实验室坐标系下,由于多普勒频移效应fD而分裂成多支频率不同的结构.实验室坐标系下4 支BAEs 不稳定性的频率范围为50 kHz ≤fBAE,lab≤60 kHz,相邻分支的BAEs 频率差值为 ΔfBAE≈2.5 kHz.按照R≈2.02 m 附近的等离子体参数进行评估,Te=1.5 keV,Ti=0.75 keV,ne≈3×1019m-3,Bφ ≈2.06 T,vA≈5.6×106m/s,fD≈2.6 kHz≈ΔfBAE(fD=vφ/(2πR),环向旋转速度vφ ≈33 km/s).利用(3)式估算BAE-CAP频率为fBAE-CAP=41kHz.考虑多分支BAEs的环向模数范围为n=1 − 5,利用(3)式可以估算BAE 连续谱极值点的频率值44 kHz ≤fBAE-CAP+nfD≤53 kHz,符合动理学比压阿尔芬本征模(KBAE)的频率特征.(3)式只能估算BAE 连续谱极值点(BAE-CAP)附近的频率,而快离子效应或热粒子动理学效应带来的频移修正,需要额外的模拟计算.
从(1)式可得出,当qmin=m/n=2和Δω=0同时满足时,ωRSAE,min≡ωBAE(RSAEs 的起始频率点,fBAE≈50 kHz).从(2)式可以得出,当qmin发生改变并随时间减小时,不同RSAE 分支的扫频斜率随着m的增加而成倍增加.从图5 可以看出,离轴锯齿振荡期间的RSAEs 向上扫频可达到的最高频率约为f ≈85 kHz (m/n=2/1),远 未达 到TAE 的本征频率(f <fTAE≈vA/(4πqR)≈110 kHz).可能的因素包括: 1) 高能束离子的能量偏低(Eb≤60 keV),束离子的初始速度vb≤2.4×106m/s (vb≤0.4vA),而慢化后束离子的速度将远远小于阿尔芬速度;2) 在qmin=2 的条件且保持q剖面不变时,RSAE 模的频率正比于等离子体热压力[54],此时等离子体的归一化比压βN≤1.
为了更好地理解阿尔芬不稳定性的激发和不同参数之间的依赖关系,把放电条件相类似的两炮#60212 和#60223 进行直接对比分析,结果如图6 所示.由于#60212 和#60223 中NBI 系统的关闭时刻不一样,为了直观对比,把#60212 这一炮的时间轴整体往前移动 Δt ≈590 ms.这两炮中采用不同入射角的中性束束线NBI1L 和NBI1R,NBI1L 和NBI1R 分别沿着平行和垂直等离子体电流方向注入中性束粒子,其中两条束线的夹角为8.7°,具体参考文献 [18,55].束输出功率和能量分别为PNB≈1.3 MW和Eb≈52 keV.在EAST 条件下,中子产额代表着氘氘快离子聚变反应的产物,因此中子产额代表着快氘离子的密度[56].此时两种条件下离轴锯齿的振荡周期和中子产额略有不同,但仍然拥有相同的等离子体储能Wdia、芯部电子温度Te0和弦平均密度ne0等宏观参数.比较有意思的是,阿尔芬本征模不稳定性只有在垂直方向注入NBI1R 的条件下才能被观察到,而在平行方向注入NBI1L 的条件未能激发,如图6(e)中的红线所示.影响阿尔芬本征模不稳定性的激发因素有很多种: 1)q剖面分布;2)热压力梯度;3)快离子分布函数;4)径向电场或流剪切等因素,如图7 所示.定义Te,Ti和vφ这3 个物理量的归一化梯度标长分别为R/LTe,R/LTi和R/Lvφ(R/LA=R/A·|dA/dr|,A=Te,Ti,vφ).
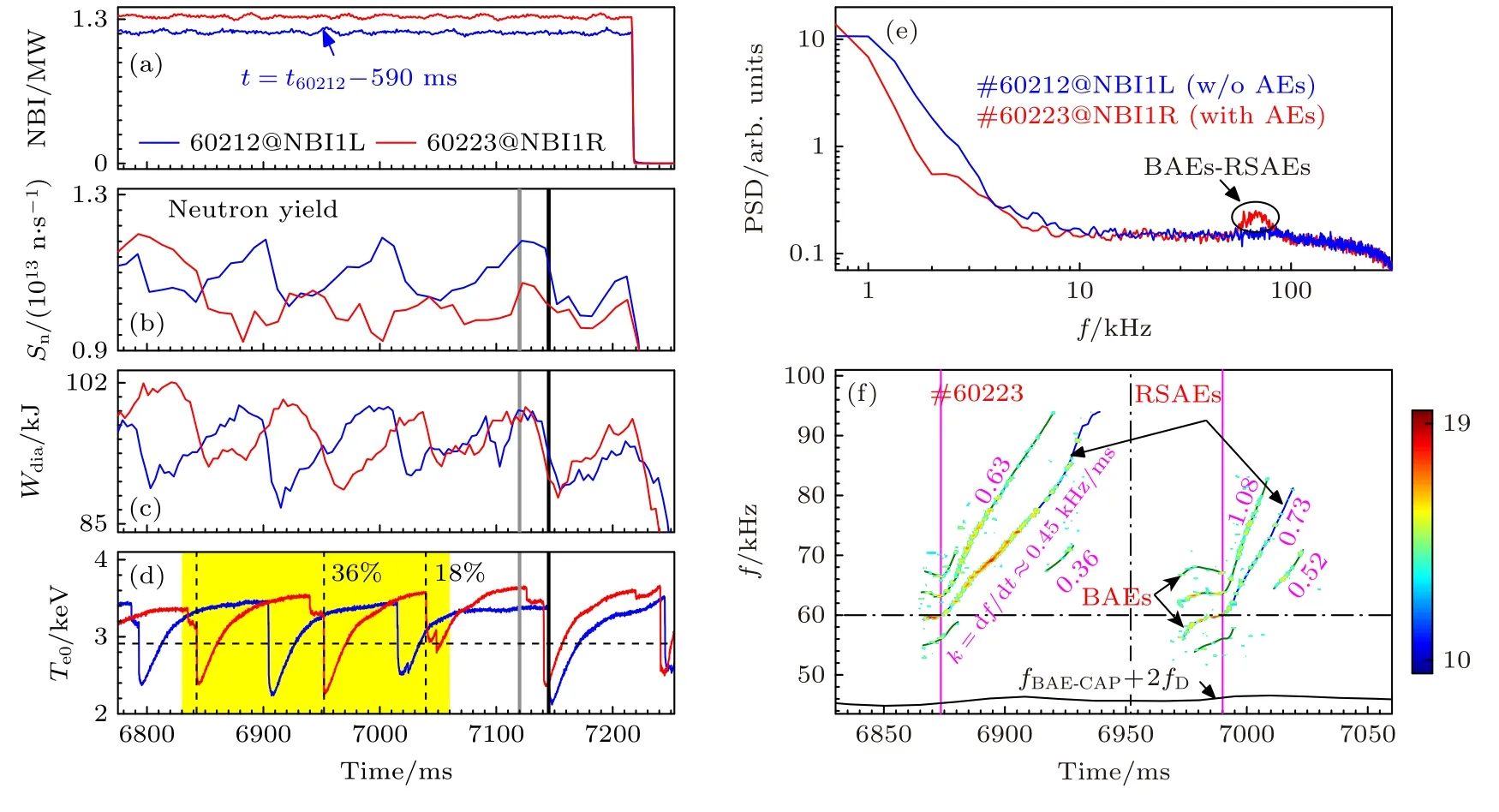
图6 EAST 上离轴锯齿振荡期间阿尔芬波不稳定性的激发条件对比 (a) NBI 功率;(b) 中子产额 Sn ;(c) 等离子体储能 Wdia ;(d) 芯部电子温度Te0 ;(e) 径向 R ≈2.02 m 附近ECE 信号功率谱;(f) #60223 下ECE信号频谱图Fig.6.Excitation conditions of Alfvén waves during the oscillation of OAS in EAST: (a) Input powers of NBI;(b) neutron yield Sn ;(c) plasma stored energy Wdia ;(d) core electron temperature Te0 ;(e) power spectra of ECE signal at R ≈2.02 m ;(f) spectrogram of ECE signal for #60223.

图7 影响阿尔芬本征模激发的3 个相关因素 (a) 温度剖面(Te 为点划线;Ti 为 实线);(b) 温度归一化梯度标长(R/LTe 为点划线,R/LTi 为实线);(c) RNC 诊断测量的中子计数率空间分布(高能离子密度);(d),(e) NUBEAM/TRANSP 代码计算不同NBI 束方向下的高能离子的经典分布函数;(f) CXRS 诊断测量的环向速度归一化梯度标长(R/Lvφ)Fig.7.Three correlated factors for the excitation of Alfvén eigenmodes: (a) Profiles of Te and Ti ;(b) normalized temperature gradients of R/LTe and R/LTi ;(c) counts of neutron flux measured by RNC;(d),(e) classical distribution functions for the two conditions are estimated by the NUBEAM/TRANSP;(f) the normalized gradient of R/Lvφ measured by CXRS.
首先,q剖面分布情况相近.两种放电条件下的等离子体约束状态相当,离轴锯齿的振荡周期接近,且等离子体内感相似(1.04 ≤li≤1.1),可以推测两种情况下的q剖面相似且满足qmin≈2.其次,压力梯度效应近似相当.两种不同方向中性束NBI1L 和NBI1R 注入条件下,电子温度的剖面基本上一致,离子温度的剖面略有不同,且在qmin位置处的电子和离子温度的梯度归一化长度分别为R/LTe≈15和R/LTi≈5,如 图7(a)和 图7(b)所示.BAE 的激发条件和压力大小之间的关系,可见文献 [44,57]中的讨论.第三,快离子分布函数不同.径向中子相机(RNC)[58]测量的快氘离子密度沿着径向的分布情况如图7(c)所示.可以看出,此时快离子的密度分布完全不同,即NBI1L (切向束)要高于NBI1R (垂直束)条件下的快离子密度.利用NUBEAM/TRANSP 代码,可以很容易计算出两种条件下高能离子的经典分布函数,如图7(d)和图7(e)所示.两种束线NBI1R 和NBI1L 方向下的高能离子偏转角(v///v)分别为v///v≈0.38和v///v≈0.65 (初始束能量Eb≈50 keV).NUBEAM/TRANSP 代码模拟结果中的快离子密度分布趋势和实验测量结果相类似.但实验测量结果更加精细,如两种情况下第二道RNC 弦信号幅值基本上一致,而其他弦信号均是NBI1R 注入条件低于NBI1L.因此,垂直束NBI1R 条件下qmin附近的快离子密度的梯度显著提高,这也是阿尔芬本征模的一个重要激发条件.最后,环向旋转速度和速度梯度完全不同.切向(NBI1L)和垂直(NBI1R)注入的中性束产生了完全不同的环向动量输入,如在R ≈2.02 m附近产生的环向旋转速度分别为vφ|1L≈50 km/s和vφ|1R≈34 km/s.从图7(f)可以看出,切向NBI1L 注入产生更强的环向流剪切,并在qmin附近流剪切大小为R/Lvφ≥3,这可能会对阿尔芬本征模的抑制起到一定的作用.因此,阿尔芬本征模不稳定性的激发强烈依赖于垂直束(NBI1R)注入条件下的快离子分布函数,而高的压力梯度起到了重要的辅助作用,但环向旋转或旋转剪切效应还不清楚.
离轴锯齿的“中心”和“环向”崩塌事件与qmin之间存在强烈依赖关系.选择图6(d)中阴影区间相邻两个离轴锯齿的振荡周期进行分析,其频谱如图6(f)所示.这两个离轴锯齿崩塌带来芯部的温度扰动分别为 ΔTe0/Te0≈36%和ΔTe0/Te0≈18%,对应着“中心崩塌”和“环形崩塌”事件.两类崩塌事件爆发之前均激发了RSAEs 不稳定性,相关结果对比如下.首先,RSAEs 的径向覆盖范围不同: “环形崩塌”前爆发的RSAEs 不稳定性只能被R ≈2.02 m处的ECE 信号所捕捉到,而“中心崩塌”前爆发的RSAEs不稳定性同时被R ≈2.02 m和R ≈2.06 m处的ECE 信号所捕获.其次,RSAEs向上扫频斜率(k ≡dfRSAE/dt) 不同: “中心崩塌”前和“环形崩塌”前的3 支RSAEs 扫频斜率分别标在图6(f)中,把2 组RSAEs 的扫频斜率放在一起,如图8 所示.依据#60223 炮相关分布参数有dfRSAE/dt ≈1.56×/dt·m.利用两种拟合曲线的交点很容易推测出RSAEs 极向模数m分别为m=2,4,6 (限制条件qmin≈2,n为连续的自然数).拟合得出“环形”和“中心崩塌”之前的qmin随时间的演化速率为≈9×10-3和≈4.4×10-3.因此,“环形崩塌”和“中心崩塌”发生的主要原因是q剖面的不同,并引起了qmin附近的梯度(cavity: dq/dr|min)和演化速率的不同.3 个RSAEs 分支最可能的模结构分别为m/n=2/1,m/n=4/2和m/n=6/3.根据BAEs-RSAEs 频谱的连续性和径向结构的一致性,进一步证明前面推测BAEs 的环向模数为n=1—5 的合理性.
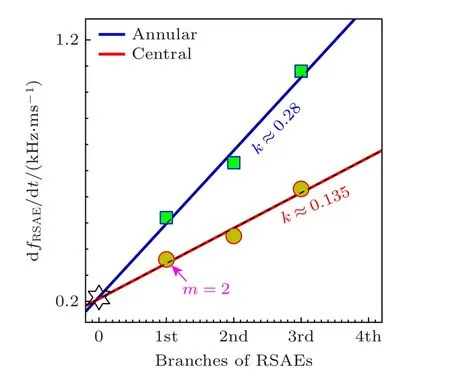
图8 两种不同类型离轴锯齿崩塌前RSAEs 向上扫频斜率对比结果Fig.8.Upward sweeping rates of RSAEs different branches before the central/annular collapse events.
5 热压力梯度激发低频模不稳定性
动理学热离子带隙(KTI)[59]频率范围内包含了3 类主要的不稳定性: 1)有限逆磁漂移效应引起的动理学气球模(KBM),在EAST[19]和DIIID[22]上又称为低频模(LFMs)或者低频阿尔芬模(LFAM)[60,61];2)热离子可压缩性而引起的比压阿尔芬本征模(BAE);3)由动理学热离子可压缩性及波-粒子共振效应引起的阿尔芬的离子温度梯度模(AITG).一般而言,AITG 剪切阿尔芬连续沉积点会转移到复频率平面[44],并导致这类不稳定性模具有短波长特征,而在实验上则表征为高的环向模数.
离轴锯齿振荡期间,热压力梯度可以激发低频模(LFMs)不稳定性.在EAST 上qmin≈2 条件下的低频模不稳定性可以分成两大类: 1)向上扫频LFMs 不稳定性;2)向上跳频LFMs 不稳定性,具体参考文献 [19].这两类不稳定性的频谱特征均可分为基频和高频两个部分: 基频部分的频率大小由离子抗磁漂移频率决定,而高频部分的频率大小和变化趋势与qmin紧密相关,且高频部分的模数远大于基频模数.两类LFMs 不稳定性的区别表现为:第一类的高频部分由基频逐渐向上扫频,如图9(b)所示;而第二类的高频部分和低频部分是相互分立的,且在模式由基频向高频跳跃时,环向模数直接翻倍(n=3 → 6),这和DIII-D 上观察的结果相类似[22,61].这里详细介绍LFMs 不稳定性的第一类情况.在反磁剪切qmin≈2 的实验条件下,当存在快离子时,热压力梯度激发的LFMs不稳定性和快离子激发的阿尔芬本征模不稳定性基本上同时发生,如图9 所示.LFMs 的演化过程中出现了基频和向上扫频两个阶段,对应着两类不同的阿尔芬本征模BAEs 和RSAEs.LFMs 的基频阶段和BAEs不稳定性同时被激发,拥有相类似的径向覆盖,且两种不同模式的存在时间基本一致,如文献 [18,19]中所描述.如图9(c)所示,随着离轴锯齿振荡周期的增 加,LFMs 和BAEs 共存 时间显著增加.在EAST 离轴锯齿的实验中发现,只要增加NBI 或ICRH 的功率,就可以使得反剪切q剖面(qmin=2)维持足够长时间不变,这也是ITBs建立和维持的实验条件.因此,LFMs 和BAEs共存的条件为qmin=2,当qmin偏离有理数2 并随着时间逐渐减小时,快离子激发的阿尔芬本征模由BAEs 转换为RSAEs 不稳定性,而压力梯度激发的LFMs 不稳定性环向模数突然增加.LFMs 和RSAEs 的频率随着qmin减小同时向上扫频,且LFMs拥有和RSAEs 相类似的色散关系:
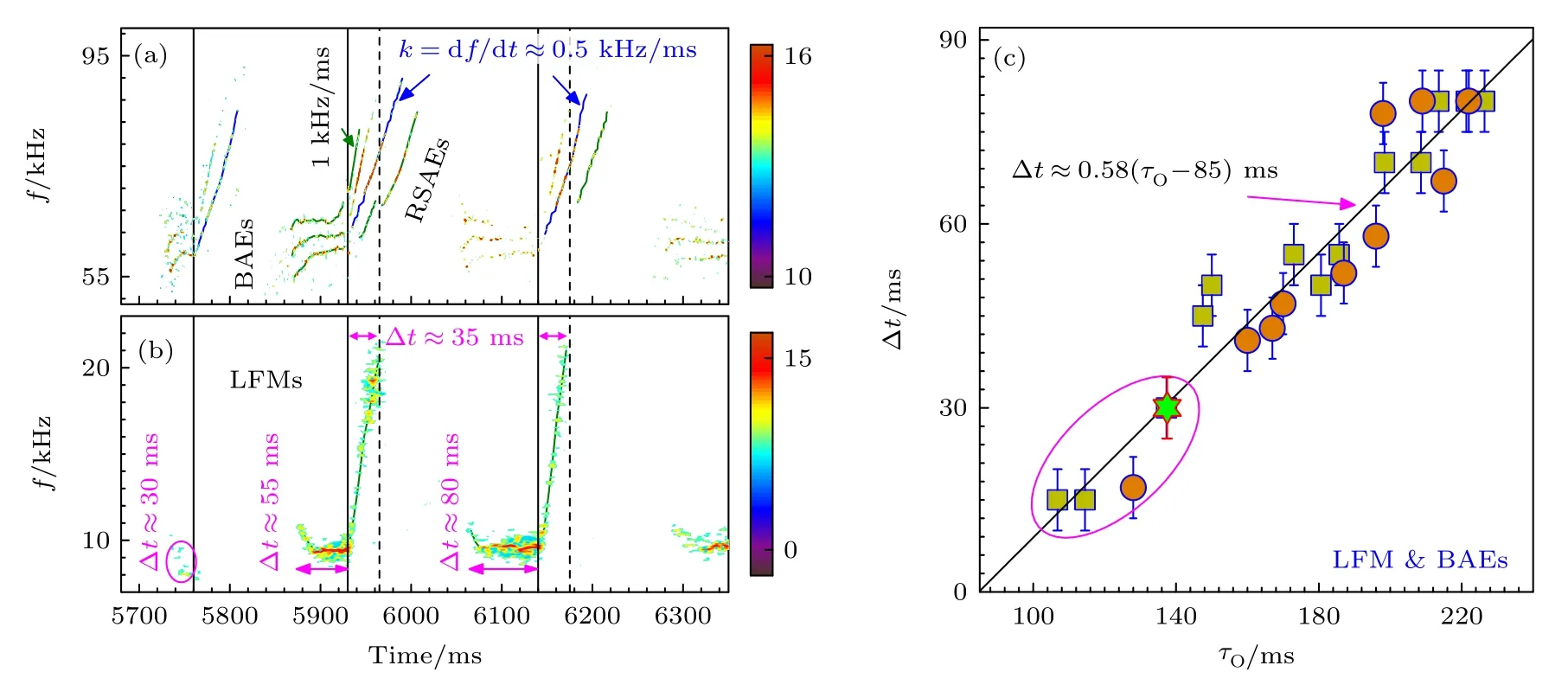
图9 低频模和阿尔芬本征模之间的共存关系 (a),(b) BAEs-RSAEs 和LFMs 的频谱图;(c) LFMs 和BAEs 的共存时间正比于离轴锯齿的振荡周期Fig.9.Coexistence between LFMs and Alfvén eigenmodes: (a),(b) The spectrogram of the pairs of BAEs-RSAEs and LFMs;(c) the coexistence time between LFMs and BAEs versus the OAS period.
对比LFMs 和RSAEs 频率的扫频斜率可以看出:LFMs 在 Δt ≈35 ms 的时间段内频率变化Δf ≈12 kHz,有k=df/dt ≈0.35 kHz/ms.目前,理论上还没有形成LFMs 的色散关系.根据EAST 上第一类LFMs 不稳定性,LFMs 和RSAEs 拥有相类似的扫频斜率大小,即(4)式可以表示成和(2)式类似的关系,例如,dωLFM(t)/dt ≈(2×0.35/0.5)×(vA/R)×
在EAST 上爆发离轴锯齿的多炮结果中发现,1)当交替出现环形和中心崩塌事件时,只有在环形崩塌事件发生之后(或中心崩塌事件之前)才更容易激发LFMs 不稳定性,即高的温度比τ=Te/Ti和合适的q剖面;2)当存在高能离子且振荡周期τO≥130 ms时,实验上才比较容易观察到LFMs不稳定性的爆发,如图9(c)所示.EAST 典型LFMs 不稳定性的典型激发条件如图10 所示.#61960 和#61970 这两炮的宏观参数基本上相类似,如LHCD 和ECRH 的功率分别为PLH≈3.5 MW和PEC≈0.5 MW,垂直束(NBI1R)注入功率和能量为PNB≈1.7 MW和Eb≈57 keV.两炮中快离子激发BAEs 不稳定性具有相似的频率大小、扰动幅度和径向位置.但只有在#61970 炮中,才能观察到LFMs 不稳定性的激发.此时,LFMs 和BAEs 不稳定性的径向位置基本上一致,其频率大小约为fLFM≈8.5 kHz,径向位置为1.98 m ≤R≤2.07 m.LFMs 和BAEs 均随着束方向NBI1R →NBI1L 的切换而消失,最大共存时间达到Δt ≈500 ms.需要说明的是,这两炮的弦平均密度略有不同,分别为≈3×1019m-3(#61960)和n¯e0≈2.8×1019m-3(#61970),并引起了温度剖面的改变,如图10(b)和图10(c)所示.
为了更好地理解LFMs 的激发条件和基本特征,把EAST 上相关实验参数输入到一般鱼骨模色散关系(GFLDR),得出如图11 所示的结果.可以看出,LFMs 的激发依赖于两个主要的分布参数(ηi,τ),即足够高的ηi=/和τ=Te/Ti,和分别为离子密度和离子温度的梯度标长,这里假设离子密度和电子密度相等.归一化压力梯度近似表示为α ∝(1+τ)(1+ηi),即激发LFMs 不稳定性所需要的压力梯度效应足够大,用于克服磁力线弯曲效应带来的致稳效应.而#61960 和#61970 炮中(ηi,τ)的实验参数分别为(2,0.96)和(2.93,2.3),只有#61970 炮符合LFMs 不稳定性的激发条件,且其增长率γ/2π ≥60 kHz 远大于模的评估频率Ω∗pi;exp≈0.83 kHz.数值求解还发现,LFMs 不稳定的激发和q剖面剪切度有关,如二次导数越小(弱剪切),LFMs 越容易被激发.此外,利用GFLDR 代码评估EAST 上LFMs 的基本特征,表现如下: 1) LFMs 频率落在离子抗磁漂移频率附近,并表现出反应型动理气球模特征;2) LFMs符合剪切阿尔芬波的极化方向,即极化因子满足条件 |S|≪1.依据Chavdarovski 和Zonca[62]建立的试探性标准: 模式频率和物理参数成比例的变化规律(包括极化因子S)均应具有反应型气球模特征.一般情况下,当极化因子 |S|≈1 时,表征为剪切阿尔芬波和声波之间的耦合极化方向,而只有当 |S|≪1 时,才表示剪切阿尔芬波,详细理论推导可参考文献 [62,63].
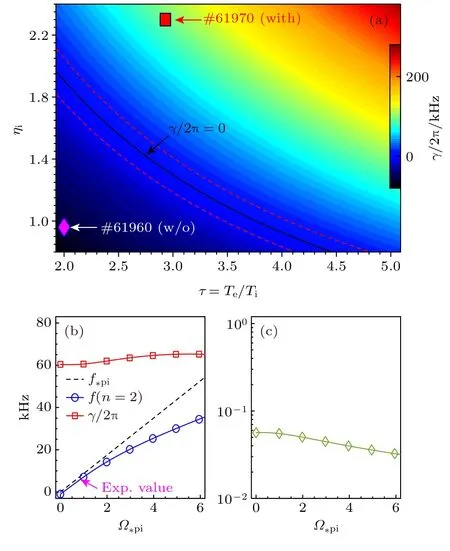
图11 利用GFLDR代码数值求解EAST 上LFMs 不稳定性的激发条件和基本特征 (a) LFMs 增长率 γ 和(ηi=/,τ=Te/Ti)之间的依赖关系;(b) LFMs 的频率f 和增长率 γ ;(c) 极化方向 |S|和Ω∗pi ≡ω∗pi/ωti 之间的关系Fig.11.Excitation conditions and basic features of LFMs are numerically calculated by GFLDR in EAST: (a) Growth rate γ of LFMs versus (ηi=/,τ=Te/Ti);(b) mode frequency f and growth rate γ ;(c) polarization |S| of LFMs on Ω∗pi ≡ω∗pi/ωti.
6 微观不稳定性的抑制及内部输运垒建立
在线性GENE 代码计算中发现,包含NBI 快离子效应可以显著抑制ITG 不稳定性,而快离子的压力剖面又会激发低环向模数的电磁模不稳定性,其频率为BAE/GAM 频率附近[39,40].最新的GENE 代码模拟[6],以及JET[4]和KSTAR[5]装置的实验结果均表明: 快离子对内部输运垒和等离子体的约束起到了重要的作用.EAST 装置建立ITBs 结构的实验结果,最早可追溯到2017年[64,65].随后,ITBs 建立过程中相继观察到RSAEs[17,66,67]和鱼骨模(fishbone)[68−71]不稳定性的爆发.此外,利用微波反射计诊断详细研究了ITBs 建立前后的湍流变化情况[72],发现弱垒情况下,内部的湍流并不能完全抑制.接下来将从EAST 内qmin≈2 条件,简要分析ITBs 和快离子及热离子压力梯度相关不稳定性.
6.1 双撕裂模的缓解和控制
从图2(a)—(d)可以看出,由于双撕裂模不稳定性的爆发,高约束态的等离子体很难长时间维持.因此,在反磁剪切位形下必须对离轴锯齿现象(或双撕裂模结构)进行有效控制.如图12 所示,#61959 炮利用LHCD 和ECRH 组合的方式(PLH≈3.1 MW和PEC≈0.4 MW),成功建立了qmin≈2 反磁剪切位形.离轴锯齿“中心”和“环形”崩塌事件交替出现,振荡周期约为τO≈100 ms.理论分析和数值模拟结果表明,通过增加旋转速度的方法可以有效解耦双q=2 面上的撕裂模不稳定性,并抑制双撕裂模的线性增长率[73,27].为了探索不同旋转速度对双撕裂模的影响程度,在#61962 中交替使用了不同注入方向NBI1R 和NBI1L 的中性束,源功率均为PNB≈1.7 MW.当使用垂直束NBI1R时,芯部等离子体芯部的旋转速度由原来vφ0≈25 km/s变成了vφ0≈50 km/s,而离轴锯齿的爆发频率也下降了一半以上,约为τO≈260 ms.当使用切向束NBI1L 注入时,芯部的旋转速度提高到vφ0≈80 km/s,并在NBI1L 注入的时间窗(Δt ≈500 ms)内,已经观察不到离轴锯齿的爆发事件,即τO>500 ms.未来将进一步进行深入研究关于利用旋转速度(或流剪切)控制离轴锯齿不稳定性相关物理问题.
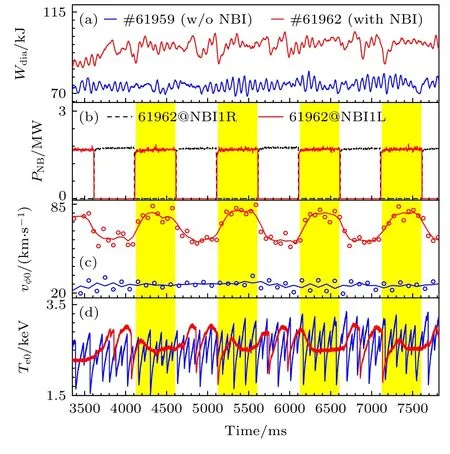
图12 利用不同注入方向的中性束(NBI1R 为垂直方向,NBI1L 为切向注入)实现离轴锯齿的缓解和抑制 (a)储能 Wdia ;(b) #61962 NBI 注入源功率;(c)芯部的旋转速度;(d)芯部电子温度Te0Fig.12.Suppression of OAS by the different injection direction of NBI: (a) Stored energy Wdia ;(b) source power of NBI in #61962;(c) central rotation velocity vφ0 ;(d) central electron temperature Te0.
6.2 电子温度梯度关联微观不稳定性
离轴锯齿振荡期间,常伴随和电子温度梯度相关联的微观不稳定性[17,18].这种微观不稳定性的激发和抑制过程,可以概括为4 个不同的阶段,如图13 所示.
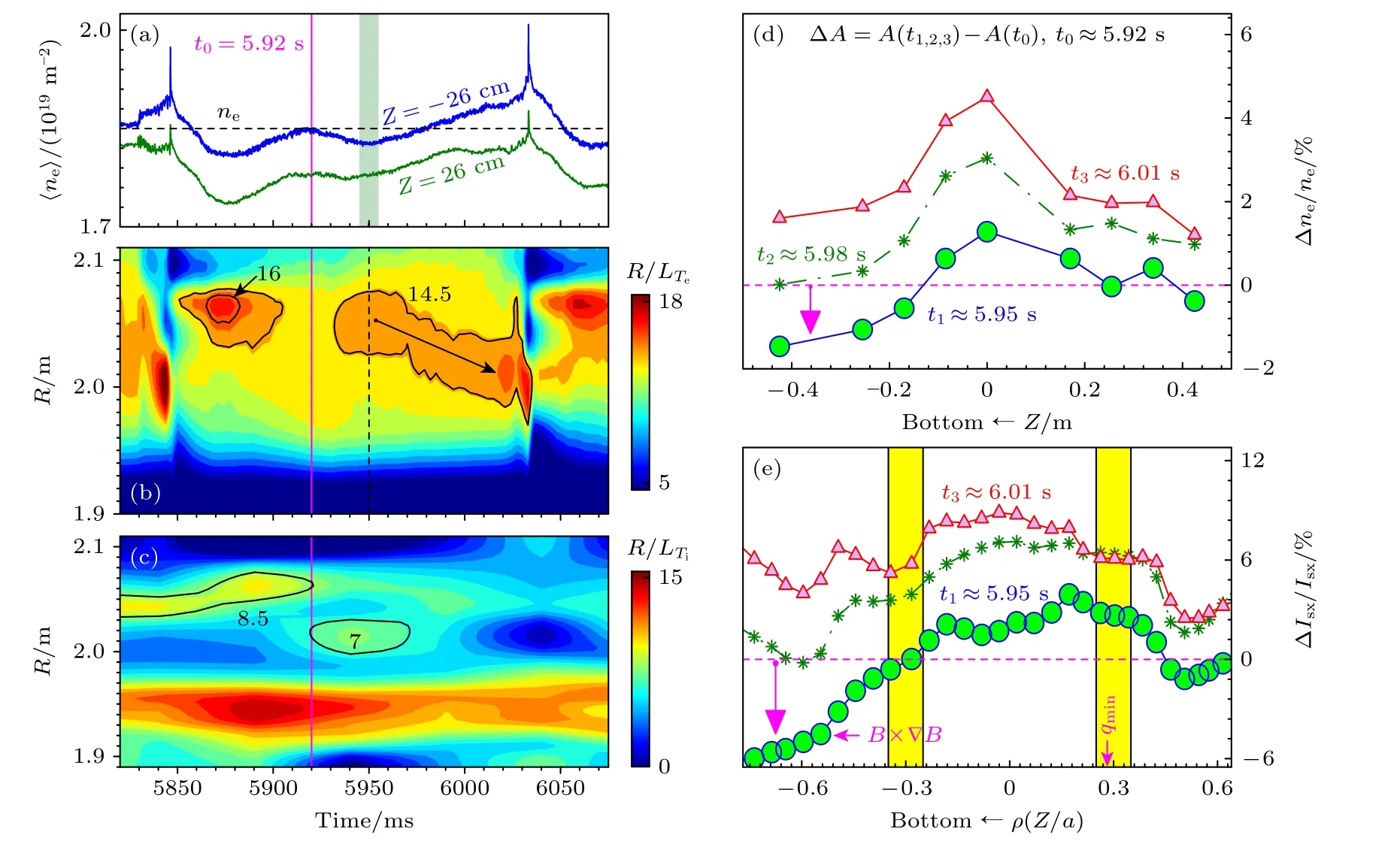
图13 离轴锯齿振荡期间微观不稳定性的激发和抑制 (a) POINT 诊断不同极向位置测量到的弦平均电子密度 〈ne〉 ;(b),(c)电子和离子温度的归一化梯度长度 R/和R/ ;(d),(e)不同环向位置POINT 和SXR 诊断测量到的相对扰动Δne/ne 和ΔIsx/IsxFig.13.One kinds of micro-instability is excited and suppressed during the oscillation of OAS: (a) Line-integrated electron densities 〈ne〉 for different chord position of POINT array;(b),(c) normalized gradient of R/ and R/ ;(d),(e) relative fluctuations of Δne/ne and ΔIsx/Isx respectively for the different toroidal positions of POINT and SXR arrays.
1)芯部电子温度的恢复和BAEs 不稳定性的激发.在前一次离轴锯齿崩塌(t ≈5.85 s)之后,芯部的电子温度迅速增加,在R ≈2.06 m 附近形成的温度梯度(R/LTe,R/LTi)显著增 大.在t ≈5.87 s 时,电子温度梯度(R/LTe≥16)和离子温度梯度(R/LTi≥8.5)达到极大值,并伴随着BAEs不稳定性模式的激发(qmin=2),如图7 中的讨论.可以看出,压力梯度效应是阿尔芬波不稳定性的激发的一个必要条件.
2)拐点的形成和RSAEs 不稳定性的激发.t ≈5.92 s时刻,出现拐点并伴随以下物理过程:Te0维持不变,但在 1.95 m ≤R≤2.1 m 区域内的电子温度梯度略有下降;Ti的离轴最大梯度区由R ≈2.06 m 跳变到R≈2.02 m (qmin).随后,在5.92 s≤t≤5.93 s时间段内,观察到阿尔芬本征模不稳定性发生模式转换(BAEs → RSAEs,如图5 所示),表明qmin偏离有理数随时间而逐渐减小(qmin<2).
3)微观不稳定性的激发和密度上下不对称性结构的出现.如图13(a)所示,EAST极向截面下半空间(Z ≈−26cm)的电子密度在t≥5.92 s后随时间逐渐减小,而上半空间(Z ≈26 cm)的电子密度近似维持不变,表现为上下(或极向)不对称性.这种不对称性在EAST 不同环向位置的POINT和SXR 诊断同时观察到,即在整个环向等离子体中均存在这种微观不稳定性.这类微观不稳定性引起的电子密度(或粒子浓度)在t ≈5.95 s 时达到最大值,在电子密度和SXR 信号上表现为Δne/ne≈2%和ΔIsx/Isx≈6% (Isx∝),如图13(d)和图13(e)中的下半空间品红色箭头所示.从图13(e)可以看出,粒子向外输运过程仅仅发生在qmin外部区域(ρ≤-0.3,ΔIsx/Isx<0).这种微观不稳定性引起粒子的输运方向沿着离子B×∇B(垂直向下)方向,这和高波数(kθ,k⊥≥9 cm-1)低频微观湍流引起的粒子输运方向一致[74],即这种微观不稳定性可能是沿着电子抗磁漂移方向传播的高波数微湍流.
4)微观不稳定性的抑制和密度上下对称结构的恢复.当t≥5.95s 时,极向截面下半空间(Z≤−26cm)的电子密度随时间逐渐增加,并伴随密度上下对称结构的逐渐恢复.不同环向位置POINT和SXR 信号上同时观察到上下对称结构的恢复,表明这类微观不稳定性的消失或抑制.实验上关联的变化有:qmin随着RSAEs 向上扫频而缓慢减小;芯部电子温度梯度(R/LTe≥14.5)向磁轴附近移动(R=2.05 m → 2 m),如图13(b)中黑色箭头所示.但是,这类不稳定性的抑制过程并未观察到离子温度或梯度的显著变化,进一步表明这类微观不稳定性的抑制和电子温度的梯度直接关联.电子最大压力梯度区由外部向中心(磁轴)区域移动的过程中,导致了q剖面的变化及双撕裂模不稳定性的爆发,在t ≈6.45 s 时刻发生离轴锯齿崩塌事件.
微观不稳定性的抑制过程(或弱ITBs 结构的建立过程)对于内部输运垒建立过程的物理理解具有重要的意义.下面首先讨论内部输运垒建立过程中的两个主要的机制: 反剪切q剖面和E×B剪切.但是这两种触发机制之间存在比较复杂的关系,例如E×B流由压力梯度效应通过新经典效应(neoclassical effect)和雷诺胁强效应(Reynolds stress)驱动,而q剖面又会受到压力梯度所驱动的自举电流的影响.因此,当某种湍流效应被抑制后,增加的压力梯度将会正反馈并进一步改变E×B流和q剖面.从图13 可以看出,在微观湍流抑制过程中,最大的电子压力梯度区(R/LTe≥14.5)由外部向磁轴附近移动,同时伴随着自举电流和q剖面的改变,即约束改善过程中两种效应E×B剪切和q剖面同时发生改变.
6.3 离子温度梯度输运垒
下面讨论EAST 上离子输运垒建立过程中的两类不同物理过程.EAST 内qmin≈2 条件下离子温度内部输运垒步骤如下: 根据前面第3 部分的讨论,利用LHCD 和ECRH 组合的方式建立反磁剪切磁位形,再注入总源功率P≥4 MW 的NBI 或ICRH 功率.图14 中分别使用了单独的NBI 注入和NBI+ICRH 相组合的方式建立了ITBs 结构.

图14 内部输运垒建立过程中伴随快离子或热粒子不稳定性事件 (a1),(a2)归一化 βN ;(b1),(b2)电子 Te 和离子 Ti0 温度;(c1),(c2) ECE 诊断测量到的频谱图Fig.14.Energetic ions and thermal pressure gradient instabilities are observed during the establishment of ITBs: (a1),(a2) Normalized βN ;(b1),(b2) electron Te0 and Ti0 temperatures;(c1),(c2) spectrogram of ECE signal.
图14 中的Case A (左列)展示了内部输运垒建立过程中伴随阿尔芬波不稳定性的激发及快离子的再分布过程.1)形成内部输运垒结构所需要的基本条件—激发离轴锯齿.图中蓝色线和深绿色线展示了两种不同的实验条件,主要区别为LHCD 和ECRH 功率不同,蓝色线PLH≈2.8 MW,PEC≈0.4 MW,而深绿色线PLH≈3.3 MW,PEC≈0.5 MW.根据前面第3 部分的分析和讨论,优化的LHCD 和ECRH 功率组合是激发离轴锯齿的重要条件.2)建立内部输运垒的过程—伴随阿尔芬波不稳定性的激发.当NBI 的总功率(PNB≈4 MW)台阶式注入等离子体中,可以观察到等离子体比压βN台阶式增加.但在t≥3.1 s 时,两种条件下的等离子体约束状态发生了显著分歧—存在离轴锯齿条件下的βN要高于不存在离轴锯齿的情况,表明内部输运垒结构的建立.爆发阿尔芬波不稳定性是这类情况下建立内部输运垒结构的另一个标志性事件.根据前面第4 部分的分析和讨论,阿尔芬波不稳定性的激发和背景热粒子及快离子紧密相关,且阿尔芬波不稳定性引起快离子的再分布,使得中子产额下降幅度达到3%.最新的理论和实验研究均表明,快离子分布函数的变化对等离子体约束的改善起到了重要的作用[4,6].
图14 中的Case B (右列)展示了内部输运垒维持过程中伴随着热离子梯度相关不稳定性.当NBI (PNB≈2.5 MW)以 后,首先在t ≈3.5 s 附近观察到向上跳频LFMs 不稳定性,如图14(c2)所示.当ICRH (PIC≈1.6 MW)注入后,芯部离子温度Ti0和βN迅速升高,标志着内部输运垒结构的形成(此时NBI 和ICRH 的总功率为4.1 MW).在ITBs 建立和维持过程中,当离子温度梯度超过某一阈值时,实验上可以观察到频率范围在75 kHz ≤f≤110 kHz 的多分支不稳定性模式.这类不稳定性的频率介于BAEs 和TAEs 之间,环向模数约为5 ≤n≤10,且扰动幅值和离子温度梯度关系密切,初步判定为AITG-like 不稳定性.根据前面第5 部分的分析和讨论,LFMs 和AITG 均位于动理学热离子带隙中的不稳定性.HL-2A 和DIII-D 的实验结果表明[75,76],AITG 不稳定性在内部输运垒和将来的反应堆等离子体中起到至关重要的作用.关于AITG 不稳定性的论证和内部输运垒之间的相关物理问题还有待进一步深入研究.
图14 中的两种情况均建立了qmin≈2 反磁剪切实验条件.Case B 实验条件包括: 在t ≈3.5 s 时爆发LFMs 不稳定性代表反磁剪切放电,在t ≈3.7 s附近出现的m/n=2/1 撕裂模进一步证明了此时的实验条件为qmin≈2.但两种情况下反磁剪切q剖面的建立方式不同,具体表现为: 1) LHCD 的功率不同,分别为PLH≈3.3 MW (Case A)和PLH≈2.3 MW(Case B).2)离轴ECRH 加热功率虽然相同,均为PEC≈0.5 MW,但注入的初始时刻不同,分别为t0=1.3 s (Case A)和t0=2.6 s (Case B).电流进入平台阶段(Ip≈0.4 MA)的时刻为t ≈2 s,则Case A 在电流分布向内渗透阶段已经开始利用ECRH 修改q剖面,而Case B 则是在电流剖面逐渐稳定后再利用ECRH 调整q剖面.
图15 详细展示了ITBs 建立前后的温度或环向旋转速度的变化情况.芯部离子温度由Ti0≈1.4 keV 增至Ti0≈2.1 keV,ΔTi0/Ti0≈50%,ΔTe0/Te0≈30%,而最大的离子温度归一化梯度长度由R/LTi≈10 增加到R/LTi≈15,表明了约束性能的大幅提升并伴随着内部输运垒结构的形成.比较有意思的是,内部输运垒feet 区域的环向旋转速度显著减小,可能的原因是与径向电场的变化有关.这里需要指出,图14 中出现的两种情况均为内外双垒的情况,这里仅仅分析了内部输运垒附近的情况.

图15 内部输运垒建立过程中温度和旋转剖面 (a) Ti ;(b) R/ ;(c) vφ ;(d)ΔTe/TeFig.15.Profiles of (a) Ti,(b) R/,(c) vφ,(d) ΔTe/Te for the establishment of ITBs.
7 结论
本文简单总结了EAST 上qmin≈2 实验条件的建立方式及表征形式—离轴锯齿和双撕裂模;并对这类条件下快离子激发的阿尔芬波不稳定性及热压力梯度激发的低频模不稳定性做了整理和分析;实现对离轴锯齿的抑制和建立内部输运垒结构过程中,常伴随阿尔芬波不稳定性或热离子梯度激发的相关不稳定性等.具体总结如下.
首先,在qmin≈2 条件下最容易爆发离轴锯齿和双撕裂模崩塌事件.1)详细讨论了EAST 上现有条件下这些模式的激发条件.2)根据离轴锯齿的特征分为三类: 中心崩塌、环形崩塌和无磁重联小破裂事件.3)离轴锯齿崩塌前常出现模结构为m/n=2/1 撕裂模的先兆振荡模,并最终形成双撕裂模的出现和离轴锯齿的崩塌过程.
其次,离轴锯齿振荡过程中常伴随BAEs 和RSAEs 不稳定性.1)展示了两类阿尔芬本征模的径向位置,并利用理论模型对频率进行估算;2)详细对比了两类相似放电条件下的阿尔芬波不稳定性的激发条件,并对关联的4 个物理参数进行对比;3)对比分析了中心和环形崩塌前的RSAEs 扫频特征,并反推出两类崩塌事件对应着不同的qmin演化曲线.
第三,离轴锯齿振荡过程中常伴随LFMs 不稳定性的激发.1)EAST 上低频模不稳定性可以分为向上扫频和向上跳频LFMs 不稳定性.2) EAST上LFMs 不稳定性的激发条件是需要强的压力梯度α ∝(1+τ)(1+ηi) (高ηi=/或τ=Te/Ti).3) EAST 上LFMs 特征表现为: 离子抗磁漂移频率大小、阿尔芬波极化方向和动理学气球模特征.
最后,抑制离轴锯齿的爆发可以高效建立内部输运垒结构.1)通过增加环向旋转速度(或快离子分布函数等)方法可以有效缓解离轴锯齿的爆发频率.2)离轴锯齿振荡初期常伴随某种微观不稳定性的激发,并在后期得到有效的抑制—拉长离轴锯齿振荡周期(缓解或抑制)可以获得更好的约束.3)内部输运垒建立或维持过程中常伴随快离子或热离子压力梯度相关不稳定性,因此,理解快离子或热压力梯度相关不稳定性,对内部输运垒形成机制的理解具有重要的物理意义.
