基于可分离替代函数优化的CT重建

侯晓文，郭金川陈伟，江浩川

1）深圳大学物理与光电工程学院，广东深圳 518060；2）明峰医疗系统股份有限公司，浙江杭州 310018

计算机断层成像（computed tomography，CT）技术［1］在临床诊断和治疗中已获得越来越广泛的应用［2-6］，与此同时，患者承受的X 射线辐射剂量也日益增高［7-12］，尤其新型冠状病毒肺炎（corona virus disease 2019，COVID-19）爆发以来，患者接受的CT扫描频次大幅增加［13］，因此，降低CT 扫描剂量具有广泛且迫切的临床需求.能谱CT 技术［14-15］（包括双能CT 与光子计数CT 等）对于低剂量扫描下的高质量成像亦有迫切需要.然而，对于传统的滤波反投影（filtered back projection，FBP）重建算法，降低扫描剂量将导致CT 图像噪声水平增高，影响医生的临床诊疗判断［1，7］.

迭代重建（iterative reconstruction，IR）算法能够在降低扫描剂量的同时，提供高质量图像［1］.IR 算法在问题描述中引入数据非理想性，并将非理想性构建到统计模型中，进而使CT 图像重建公式转化为以目标函数形式表达的正弦图数据及图像估计的统计度量.通过迭代计算，优化该统计度量，重建出CT图像.

为更好地降低图像噪声并保持算法稳定性，需在目标函数中加入图像空间分布先验信息［1］.马尔科夫随机场（Markov random field，MRF）是图像先验分布的一种典型选择［16］.使用MRF 作为先验分布能够获得仅具有局部相互作用的正则项函数.正则项函数中的势函数能够惩罚图像局部差异，从而降低图像噪声.势函数的恰当选择对迭代重建至关重要:①势函数应为凸函数，以保证目标函数最小值的全局唯一性，且可以通过较简单的优化方法求解；②势函数应具有足够的灵活性，以便灵活控制迭代重建图像噪声、空间分辨率及低对比度分辨率等特性，满足临床诊疗的不同需求.文献［16］提出的q值广义高斯马尔可夫随机场（q-generalized Gaussian MRF，q-GGMRF）同时具有凸特性和灵活性，以其为势函数的迭代重建结果在噪声及空间分辨率等方面表现优越.

但是，基于q-GGMRF 的迭代重建算法计算成本高、重建时间长.文献［16］采用迭代坐标下降（iterative coordinate descent，ICD）算法优化目标函数，在每次迭代中假定除当前图像像素外，其余像素均为常数，从而实现对目标函数的一维求导，再利用二分查找算法，求取上述一维导数的根；将上述一维优化过程遍历目标图像的所有像素点，即实现1次完整的迭代过程；通过多次迭代，使图像收敛到最优点.由于优化过程在一维进行，计算复杂度大幅降低.但是，遍历像素的过程使得重建耗时漫长，难以满足临床要求.为降低计算成本，减少重建时间，文献［17］提出一种非均匀ICD（nonhomogeneous ICD，NH-ICD）算法，根据像素选择标准自适应确定需要更新的像素，利用像素选择算法确定像素更新顺序.为加快每个像素的更新速度，NH-ICD 算法使用替代函数方法获得一维目标函数的封闭解，避免了搜素算法的多次计算.NH-ICD相对于ICD 重建速度提高了3 倍，但重建时间仍需约1～2 h，相应地FBP重建算法仅需几分钟就能完成重建.由于NH-ICD 的重建时间过长，仍难以满足临床需求.

为进一步降低迭代重建时长，本研究提出一种基于可分离替代函数优化，以q-GGMRF 为正则项统计模型的迭代重建算法.针对该统计模型目标函数为凸函数的特点，采用优化转换策略，构建恰当的可分离替代函数，将目标函数优化转换为各个像素相互独立的替代函数优化，实现各个像素的同时优化，大幅提高了算法的并行性.实验结果验证了算法的可行性.

1 统计模型和目标函数

令X=[x1，x2，…，xN]T为三维图像离散向量，即图像估计；令y=[y1，y2，…，yM]T表示投影的离散向量.首先根据统计模型，将上述X和y的统计度量关系表达为目标函数的形式.

迭代重建中假设离散向量X和y是随机向量.在CT 扫描过程中，每个探测器单元记录了穿透目标物体的X射线强度λ={λi，i=1，2，3，…，M}.根据比尔定律，λ与衰减系数线积分相关，且λi～，其中，Ii是入射X 射线光子强度；是理想的无噪声线性衰减系数线积分.

根据贝叶斯公式

其中，P表示概率.取负自然对数后得

图像估计X和投影测量y采用如下线性模型

其中，A为系统矩阵；向量n中每一分量对应光子噪声和电子噪声强度.λ和y满足比尔定律，且服从泊松分布，式（1）等号右边第1 项可通过二阶泰勒级数展开，以足够的精度近似为

其中，f（y）是关于y的函数，与X无关，可忽略；D=diag{d1，d2，…，dM}是对角权重矩阵，反映测量数据固有可信度.对于临床CT范围内的泊松计数，上述近似足够精确.

系统矩阵A和权重矩阵D的恰当选择对于重建速度和最终的重建图像质量至关重要.文献［16］采用距离驱动（distance driven，DD）系统矩阵模型，可以在保持CT 系统扫描几何结构精度下快速实现正反投，兼顾了计算时间和重建精度.本研究采用相同系统矩阵模型.CT扫描中，D的对角元di∝λi.

式（1）中等号右边第2 项是图像估计先验分布的负对数，等于目标函数正则项R（X）加1个常数.R（X）用来控制图像估计的噪声，并保证算法的稳定性.图像估计先验分布的典型选择是马尔科夫随机场，本研究采用基于MRF的正则项形式为

其中，参数p用来平衡图像降噪和边界保持，p值增大，降噪水平增强，边界保持减弱；参数σ为标量，控制图像估计中相邻像素集合Sj所定义的局部邻域上，相对于噪声模型的先验强度，参数值根据经验确定；bj，h是方向加权系数，采用中心像素和Sj中第h个元素之间距离的倒数，并进行归一化，即=1；ρ（·）为势函数，用来惩罚局部差异，本研究采用文献［16］提出的q值广义高斯马尔可夫随机场所用的势函数，即

其中，参数q用来保持图像边界，p固定时，q值越小，图像边界信息保持越好；参数c用来确定边界的强弱，其值增大时，表示更大像素差值Δ才被当作边界.

当1≤q＜p≤2时，式（3）和式（4）所示的正则函数是严格凸的.此外，参数p和q为调节图像估计的噪声及空间分辨率等提供了更好的灵活性.

结合式（1）—式（4），可得用于迭代重建的目标函数为

其中，H（X）为目标函数的数据拟合项，

因此，CT 图像重建问题等价为根据统计模型构建的上述目标函数的最小化问题，即

2 可分离替代函数优化算法

对式（7）所示的目标函数进行优化非常困难，文献［16］和［17］分别采用ICD 和NH-ICD 算法进行优化.但由于需要对所有像素逐个优化，导致迭代重建耗时过长，无法满足临床要求.本研究基于目标函数的凸特性，利用优化转换原理，将优化过程转换为对可分离替代函数的优化.可分离替代函数具有并行性高的优点，结合图形处理器（graphics processing unit，GPU）技术，能够极大提高迭代重建计算速度.

2.1 优化转换原理

优化转换是在第k次迭代中，用容易优化的替代函数Lk（t）取代难以优化的目标函数L（t），替代函数的最优点是目标函数的第k+1次估计，即

由此可得估计数列｛tk｝.若每次迭代构建的替代函数满足

则数列｛tk｝将使目标函数单调下降.其中，Ω是L（t）的定义域.若目标函数是凸函数，数列｛tk｝将收敛到目标函数最小值点.

此外，替代函数还具有如下性质.

文献［16］已经证明，式（7）中的目标函数是凸函数，因此，可以利用上述优化转换原理计算全局最优值.基于此，文献［17］对每个一维优化过程采用优化转换方法替代二分查找方法的算法，提高了迭代重建速度.但其构建的替代函数仅适用于一维优化过程，总的迭代过程仍需要遍历所有需要优化的像素点，导致迭代时间仍然很长.本研究基于优化转换原理，根据目标函数的具体特征构建一种可分离替代函数.

2.2 替代函数

由式（5）可知，L（X）为数据拟合项H（X）和正则项R（X）的和.根据引理1，分别推导H（X）和R（X）的替代函数，并以二者替代函数的和作为L（X）的替代函数.

2.2.1 数据拟合项替代函数

将式（6）改写为

其中，Ai表示系统矩阵A的第i行.由式（12）可见，H（X）为M个凸函数的和，且这些函数形式相同.根据引理1，可先推导这些凸函数的可分离替代函数，然后以其和作为H（X）的可分离替代函数.记

其中，Hi（X）是关于X的凸函数，但各个元素不可分离.为实现所有像素同时优化，保证迭代并行性，为Hi（X）构建逐个像素可分离的替代函数.

首先，构建一组组合系数

2.2.2 正则项替代函数

由式（3）可得，正则项函数由一系列具有相同形式势函数ρ（xj-xh）的线性组合构成.ρ（xj-xh）为凸函数［16］，则其可分离替代函数为

因此，式（17）的替代函数满足式（8）和式（9）.

据引理1，正则项函数满足式（8）和式（9）的可分离替代函数为

综上可得，目标函数满足式（8）和（9）的可分离替代函数为

2.3 优化

式（7）所示的CT迭代重建优化过程可转换为

由于Lk（X）的各个像素可分离，可同时对所有像素进行优化.不失一般性，以下以像素xj的优化为例，推导式（20）优化过程的更新公式.结合式（15）—式（18）对Lk（X）求xj处的导数，并令其为0，即

由式（21）—式（24）可见，像素点xj的更新只与该像素点本身以及图像估计的上一次迭代结果有关，与图像估计中其他像素当前迭代过程无关.因此，各个像素点可以同时更新.

求解式（21）的根即可得到xj的更新.该方程的根难以计算封闭解，参考ICD方法，采用二分查找方法求解.

3 实验和结果

为评估算法性能，采用明峰医疗ScintCare CT 128 第3 代CT 扫描系统采集数据，分别采用FBP、ICD 及本算法重建图像.其中，ICD 算法和本算法中用来控制图像质量的参数（p、q、c和σ）值依据文献［16］中的最优参数值选取.

3.1 模体实验

采用明峰医疗ScintCare CT 128 头颅轴扫协议，64 mm × 0.625 mm开口，管电压为120 kV，管电流为100 mA，扫描转速1 s，扫描Catphan®500 模体CTP528空间分辨率模块.FBP、ICD及本算法对上述扫描数据的重建结果如图1.重建图像层厚为0.625 mm，像素大小为0.488 3 mm × 0.488 3 mm，窗位和窗宽为［680，1］，单位为Hounsfield 单位（HU）.模体的中心区域由相同物质组成，在中心区域选择感兴趣区域（region of interest，ROI）来评价图像噪声水平.图1的σ表示圆形ROI中各像素CT值的均方根误差，即图像噪声水平，单位为HU.

图1 （a）FBP、（b）ICD和（c）本算法对Catphan® 500模体的重建结果Fig.1 The reconstruction results by（a）FBP，（b）ICD and（c）algorithm proposed in this paper for Catphan® 500.

由图1 可见，FBP、ICD 和本算法所重建图像的空间分辨率相同（12 lp/cm），但ICD 算法与本算法的噪声水平约为FBP 的50%，且二者非常接近.因此，本算法保持了ICD算法既能降低噪声水平又能保持空间分辨率的优异性能，其在图像质量上的表现与ICD基本一致.

为比较ICD与本算法的收敛速度，对重建过程的归一化均方根误差（normalized root mean square error，NRMSE）γ进行测量.γ计算为

其中，上标0 和k表示迭代次数，设置迭代终止条件为γ（Xk）≤0.01.记录每次迭代的NRMSE，以及迭代终止时相应的迭代次数与消耗时间.NRMSE与迭代次数的关系见图2.迭代终止时，ICD 与本算法所需的迭代次数与消耗时间见表1.

表1 模体实验迭代终止所需迭代次数和消耗时间Table 1 Number of iterations and time consumed for iteration termination about phantom experiment

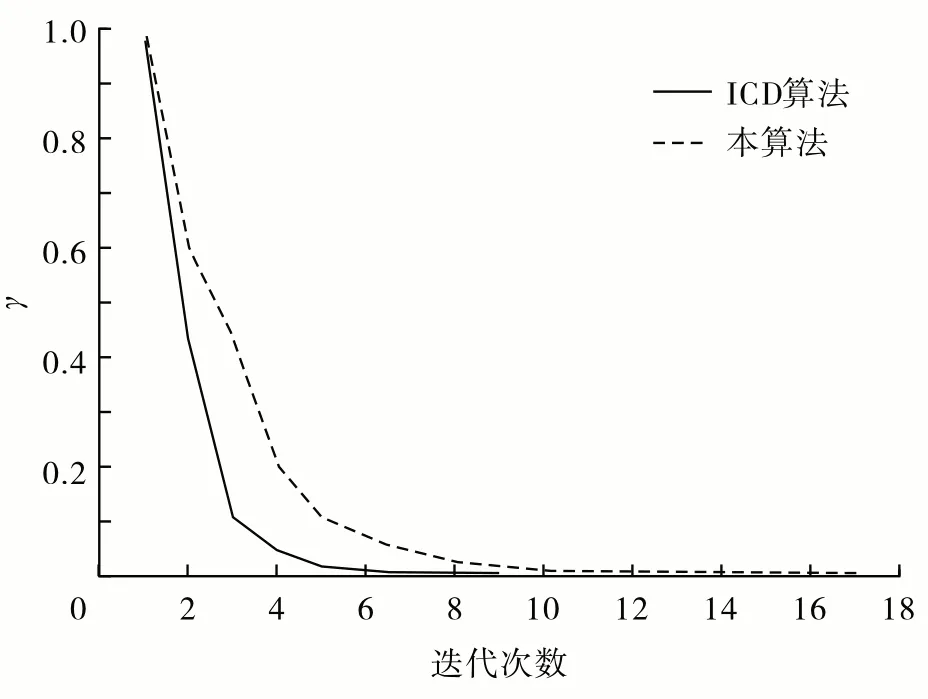
图2 ICD及本算法的NRMSE变化曲线Fig.2 NRMSE profiles of ICD algorithm (solid line) and algorithm proposed in this paper (dashed line).

由图2 可见，ICD 算法的RMSE 随迭代次数下降的速度比本算法要快，这是因为本算法中构建的可分离替代函数需要满足式（8）和式（9），每次迭代所得的最小值点略大于ICD方法，即迭代步长相对较小，导致NRMSE 随迭代次数下降的速度相应变慢.NRMSE 曲线变化速度表明ICD 算法收敛速度明显快于本算法.表1中迭代终止所需迭代次数的对比同样验证了上述结论.

然而，对比迭代终止消耗时间，本算法耗时远小于ICD算法.这是因为本算法中每次迭代所有像素同时更新，使得迭代耗时大幅降低.因此，本算法中即使迭代次数增加，总的迭代耗时反而降低.

3.2 临床结果

真实临床数据重建成功与否对算法有效性至关重要.采用明峰医疗ScintCare CT 128 腹部螺旋扫描协议，64 mm × 0.625 mm 开口，扫描人体腹部，分别利用FBP、ICD 和本算法进行重建，重建图像层厚为0.625 mm，像素大小为0.976 6 mm ×0.976 6 mm，窗位和窗宽为［60 HU，400 HU］，结果如图3.ICD 和本算法的迭代终止条件与前文模体实验相同.

图3 （a）FBP、（b）ICD及（c）本算法的临床实验结果Fig.3 The reconstruction results by（a）FBP，（b）ICD and（c）algorithm proposed in this paper for clinical experiment.

图3中σ表示小圆形CT值的均方根误差，即噪声水平，单位为HU.由图3可见，ICD算法与本算法的噪声水平约为FBP 的50%.此外，在ICD 和本算法重建图像中，一些软组织和小血管清晰可见，而在FBP图像中则被严重的噪声覆盖，难以清晰观察；观察图中肋骨可见，ICD和本算法都能够保持与FBP 相当的肋骨边界，即具有相近的空间分辨率.综合来看，ICD 和本算法显著降低噪声水平，提高了临床图像质量；本算法重建图像质量与ICD基本相同.

迭代终止时，ICD和本算法所需迭代次数与消耗时间如表2.可见，ICD 方法迭代次数少，收敛速度快，但耗时更长；本算法迭代次数较多，收敛速度较慢，但重建耗时极大降低.本算法在取得与ICD算法基本相同的图像质量同时，极大降低迭代重建所需时间.

表2 临床实验迭代终止所需迭代次数和消耗时间Table 2 Number of iterations and time consumed for iteration termination about phantom experiment

结语

针对采用q-GGMRF 正则模型的CT 目标函数，基于优化转换思想，提出一种并行优化目标函数的迭代重建方法.利用目标函数凸特性，构建满足特定条件的可分离替代函数，结合GPU 并行运算优势，在保证迭代重建图像质量的同时，极大降低了迭代重建的耗时.模体实验结果表明，本算法能够获得与ICD相同的空间分辨率和噪声水平，重建耗时仅为ICD算法的1/20.临床数据重建结果验证了本算法的临床有效性.接下来研究将集中于把本算法推广至能谱CT 成像技术，以期在低剂量扫描情况下，获得高质量的能谱CT 图像.近年来深度学习方法在CT重建领域得到越来越多的关注和应用，展现出优异的重建图像质量.本算法中的参数值通过经验确定，方法繁琐且难以得到最优值.将来研究中，可以利用深度学习方法对算法相关参数进行估计，从而自适应确定最优参数值，进而获得最优质量重建图像.