石灰岩粗颗粒湿化接触力学特性
2023-11-23王子寒刘建泽景晓昆肖成志黄达
王子寒,刘建泽,景晓昆,肖成志,黄达
河北工业大学土木与交通学院,天津 300401
粗粒土因承载力高、透水性强、压实性能好、抗剪强度高等工程特性,被广泛应用于公路、铁路、堤坝和土石坝等建筑工程中.近年来,关于粗粒土试验与数值模拟的研究不断深入,取得了丰硕成果[1-2].其中,离散单元法能够更加接近散体颗粒的实际工程性质,从而得到了广泛的应用[3-5];但是针对粗颗粒体的离散元数值分析中,粒间接触参数难以通过试验直接测试,目前仍以数值反演和参数试算为主,降低了使用效率.
目前针对粗粒土体颗粒间接触的研究主要从粗粒土体颗粒的破碎规律[6-7]和粒间接触力学性质[8-9]两个方面展开.从颗粒破碎规律方面来看,ZHAO等[10]将粒间接触形式简化为点-点和点-面接触,研究了法向受压条件下,材料、接触形式以及颗粒尺寸对粗粒土接触破碎特性的影响.YU 等[11]研究了石膏球和刚性板之间法向受压破碎,并通过数值模拟手段探究了点-面接触形式下球形颗粒内部破碎过程的力学机理.周健等[12]以大理岩球形颗粒为试验材料,通过开展双轴试验研究了在不同接触方式下的球颗粒间接触特性并将试验结果引入颗粒流程序(particle flow code,PFC)进行数值计算,直观显示了颗粒破碎的发展过程.此方面的研究重点是土体颗粒的破碎特性,主要是在微细观层面探究宏观特性潜在的细观力学机理.从粒间接触力学性质及其与宏观响应关联等方面来看,徐小敏等[13]基于土体细观与宏观参数间的联系,使用线性模型建立了颗粒体的细观参数与颗粒集合体的宏观参数之间的经验公式.丁秀丽等[14]以土石混合体的细观结构为基础,利用主-从接触面模型、渗流及强度理论对使用数值计算模拟非饱和土石混合体特性提出了具体的建模方法.赵凯等[15]对砂砾混合料开展三轴排水剪切试验,基于颗粒接触理论,提出最小孔隙比的混合料接触状态临界条件确定方法.颗粒间细观接触性质的研究有助于在离散元数值分析中获得更加准确的接触参数,提高粗粒土体宏观力学模拟的科学性与准确性.
目前对于粗粒土湿化特性的研究大多以颗粒集合体为研究对象,通过大三轴或大直剪试验研究其湿化变形规律[16-17].而对于颗粒间接触力学性质的研究大多数并未考虑材料的湿化状态,即在自然风干状态下开展力学试验.应当指出,处于湿化状态时颗粒间的接触特性与风干状态并不相同,尤其是以粒间摩擦力为主的切向接触力.另外,实际工程中的粗颗粒体并不总是处于干燥状态.
为了探究石灰岩粗颗粒湿化接触力学特性,本研究根据不同湿化状态下的粗颗粒接触力学试验研究颗粒接触力学特性,建立颗粒间接触经验模型并将其引入离散元软件中,用于对粗粒土体宏观力学特性的仿真模拟,并采用大型直剪试验对该粒间接触模型进行实际测试和模型验证.
1 粗颗粒湿化接触试验方案
1.1 试验设备及材料
本试验所用主要仪器是中国长春机械科学研究院研制的ZXB-500 型岩石双轴流变试验机,如图1(a)所示.试验机竖向最大压力为500 kN,水平向最大推力为300 kN,测力精度为5 N,变形量测精度为0.001 mm,可对岩石等块体材料进行单轴/双轴加载的蠕变或应力松弛测试,满足试验要求.

图1 试验设备(a)岩石双轴流变试验机;(b)湿化装置;(c)辅助夹具Fig.1 Testing equipment of (a) rock biaxial rheological testing machine,(b) humidifier,and (c) auxiliary fixture.
湿化箱置于加载平台上,内含湿度计和橡胶手套;通过导气管外接加湿器,实现对颗粒的湿化,如图1(b).结合强力磁条、滚排支座和刚性垫块等辅助加载夹具,对颗粒施加法向与切向荷载,法向荷载的施加沿粗颗粒的竖直方向,切向荷载的施加沿颗粒接触面的水平方向,如图1(c).
岩土粗颗粒之间的接触形式主要包括点-点接触、点-面接触和面-面接触等[18].受土颗粒的形状、大小和排列方式等因素影响,面-面接触数量有限,点-点接触不够稳定,因此点-面接触应是颗粒之间的主要接触形式.本研究制作了粒径为5 cm的立方体颗粒和正四棱锥形颗粒,正四棱锥形颗粒由长方体底座和四棱锥构成,锥体高度为颗粒高度的1/2.试验石材选择常用石灰岩,经试验测试可知,其密度为2.69 g/cm2,抗压强度为96.4 MPa,抗剪强度为30.0 kPa,压缩模量为45.5 GPa,泊松比为0.25.
1.2 试验方案
粗颗粒由干到湿再到被浸泡,其中存在的水主要有两种状态:一是颗粒表面吸水至完全润湿;二是表面湿润后入渗到颗粒全部孔隙至浸泡饱和[19].将试件湿化状态划分为自然风干、表面湿润和浸泡,对于自然风干态的试件不作特殊处理.表面湿润态通过向湿化箱内以1 500 mL/h通入水蒸汽,记录颗粒表面水汽成股流下时所需时间,同时记录湿化箱内加湿前后湿度的差值,将加湿时间和湿度差值作为粗颗粒达到表面湿润态的标准.结果显示,试件达到表面湿润态需加湿7 min,加湿前后的湿度差值约为33%.浸泡态采用自然浸水法进行处理,将试件浸泡在无压水中,间隔5 min取出称量,结果显示60 min后试件质量达到稳定.
试验分组情况如表1,颗粒湿化的法向和切向接触试验采用荷载递增的方式开展.在切向接触试验中需固定法向接触力,并按照相同湿化状态下法向接触试验中峰值法向力的大小,将法向力分成3~4 级开展颗粒切向接触试验.在法向接触试验中,自然风干、表面湿润和浸泡试样的峰值法向力分别为8、7 和5 kN,据此确定切向接触试验中的法向荷载如表1.
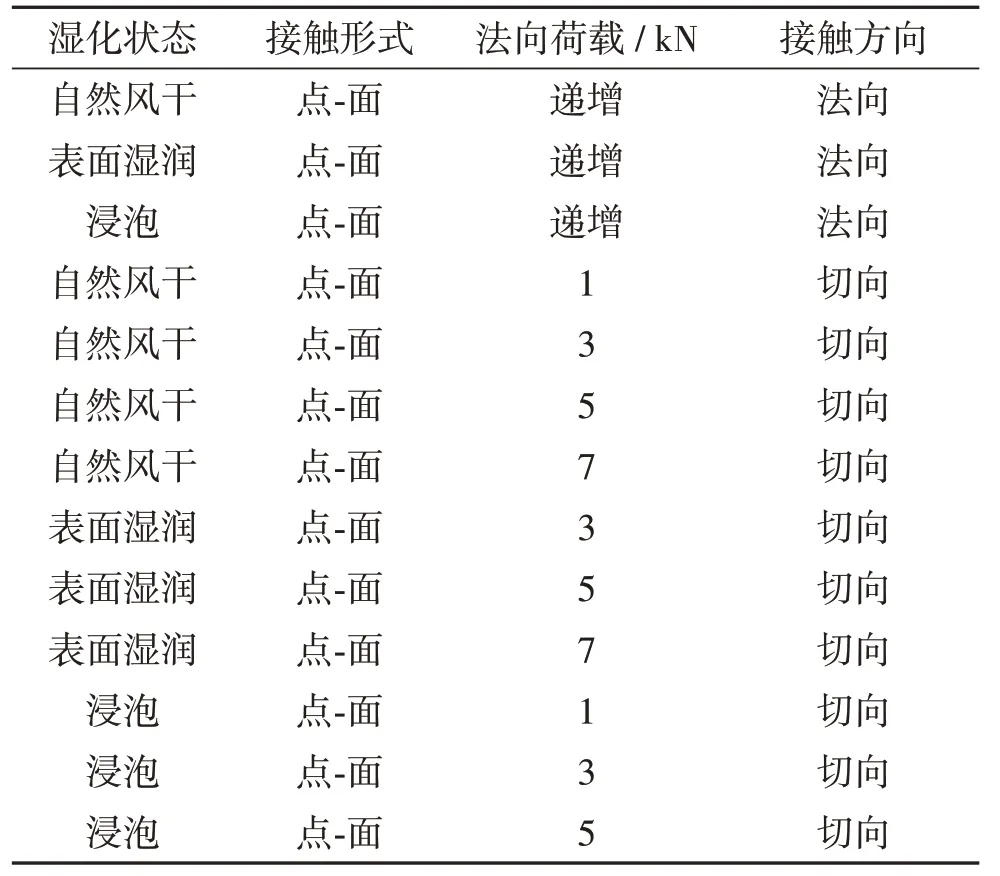
表1 颗粒湿化接触试验分组Table 1 Test groups of particle wetting contact
试验前颗粒和设备的接触面需进行润滑处理,防止摩擦力的干扰.颗粒湿化法向、切向接触试验均采用5 N/s的加载速率进行,直至试样被破坏.
2 颗粒湿化接触试验结果及分析
2.1 粗颗粒湿化法向接触试验
图2为不同湿化程度的颗粒间法向接触试验破坏形态,从整体上看,不同湿化状态的锥体颗粒凸起部分逐渐破碎并剥落,接触点变成凹凸不平的接触面.接触点的破坏随湿化程度的加深变得更加严重,随着湿化程度的加深,锥体颗粒凸起部分受挤压形成的接触面面积更大且更不平整,其中侧棱部分破碎更加严重.

图2 湿化法向接触破坏形态(a)自然风干;(b)表面湿润;(c)浸泡Fig.2 Wetting normal contact damage forms of (a) air drying,(b) surface wetting,and (c) soaking.
图3 为石灰岩湿化点-面接触法向力-法向位移关系(即法向刚度曲线)及其拟合曲线.其中,Fn为法向力;Un为法向位移.由图3可见,不同湿化状态的法向接触刚度曲线规律一致,随着接触点在加载过程中逐渐破碎和剥落,曲线总体上呈略向下凹的增长趋势,采用指数大于1的幂函数对曲线进行拟合,效果良好.

图3 湿化法向接触刚度曲线Fig.3 Wetting normal contact stiffness curves.Square,triangle and rhombus symbolic lines are testing results of air drying,surface wetting,and soaking,respectively.Black,red,and blue dashed lines are fitting curves of air drying,surface wetting,and soaking,respectively.
粗颗粒吸水后会产生一定程度软化,与自然风干试样相比,表面湿润试样法向接触刚度(曲线斜率)略小;而浸泡试样的法向刚度明显减小.由于试验曲线上存在接触点破碎产生的跳跃点,拟合函数虽然无法模拟破碎过程,但拟合出的湿化法向接触刚度能够反映实际颗粒破碎性质.
根据图3拟合曲线,粗颗粒湿化法向接触刚度可表示为
其中,a0和b0为自然风干状态下法向接触刚度曲线拟合参数;αn为法向湿润折减系数,βn为法向浸泡折减系数,两者统称为湿化法向折减系数.由于颗粒的湿化状态划分是由自然风干到表面湿润再到浸泡至基本饱和,颗粒的湿化程度是不断加强的,因此,以自然风干状态下的拟合参数为基础,引入湿润折减系数和浸泡折减系数,取值如表2.

表2 法向刚度曲线拟合参数Table 2 Fitting parameters of normal stiffness curves
通过表2中的数据换算可得,表面润湿约造成颗粒法向接触刚度(曲线斜率)减小14%;而浸泡造成法向接触刚度约减小46%,湿化水平对于粗颗粒法向接触性质影响非常明显.
2.2 粗颗粒湿化切向接触试验
根据粗颗粒法向接触试验结果,在不同级别法向力下进行粗颗粒切向接触试验(表1).在切向加载条件下,石灰岩锥体颗粒原本凸起的部位被剪切成较平整的接触面,且接触面的面积与划痕随湿化程度的加深而增大;当石灰岩颗粒吸水达到一定程度时,立方体颗粒由于吸水软化,在接触力较大时会沿接触面产生剪切破碎滑移面,如图4.
对比不同湿化状态下的石灰岩锥-面接触切向力-切向位移关系曲线(图5).可见,曲线形态呈现波动上升,湿化后的曲线在试验初期与风干态相比差别较小;随后湿润态与浸泡态曲线与风干态间的差值不断增大,尤其是浸泡态,体现了湿化作用对材料刚度的降低.

图5 湿化切向接触刚度曲线(a)湿润态对比风干态;(b)浸泡态对比风干态Fig.5 Wetting tangential contact stiffness curves of (a) contrast surface wetting and air drying: solid or hollow square,circle,and triangle symbolic lines are for surface wetting or air drying of Fn=3,5 and 7 kN,respectively;and (b) contrast soaking and air drying: solid or hollow square,circle and triangle symbolic lines are for soaking or air drying of Fn=1,3 and 5 kN,respectively.
对切向接触试验的切向力-切向位移关系曲线观察发现,大致在切向位移5 mm 左右,所有曲线的增长趋势都变缓,并逐渐趋于水平,此时的切向力大致与法向力成正比,由此采用(Us/ 5)的形式对切向刚度数学表达式进行幂函数拟合(图6):
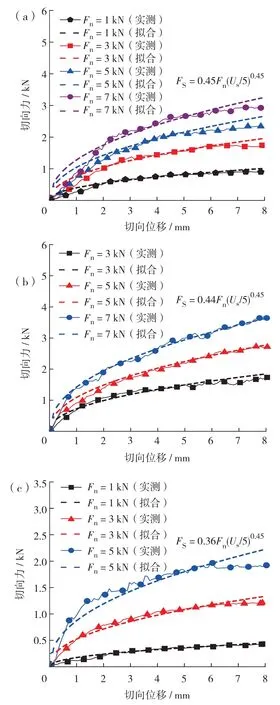
图6 湿化切向刚度拟合曲线(a)自然风干;(b)表面湿润;(c)浸泡Fig.6 Fitting curves of wetting tangential stiffness of(a)air drying: black pentagon,red square,blue triangle,and purple circle symbolic lines are for testing of Fn=1,3,5,and 7 kN,respectively;(b)surface wetting: black square,red triangle and blue circle symbolic lines are for testing of Fn=3,5,and 7 kN,respectively;(c)soaking: black square,red triangle and blue circle symbolic lines are for testing of Fn=1,3,and 5 kN,respectively.Dashed lines of the same color are for corresponding fitted results.
其中,Fs为接触切向力(单位: kN);Us为切向位移(单位: mm);c0和d0为自然风干状态下切向接触刚度曲线拟合参数,αs为切向湿润折减系数,βs为切向浸泡折减系数,统称为湿化切向折减系数;湿化切向折减系数的确定方法与法向折减系数一致,其取值情况如表3.

表3 切向刚度曲线拟合参数Table 3 Fitting parameters of tangential stiffness curves
根据表3 可知,表面湿润对于切向接触刚度(曲线斜率)影响很小,仅降低了2%;而浸泡的影响较大,切向刚度约降低了20%,吸水后软化对石灰岩颗粒切向接触刚度影响明显.
3 湿化接触刚度在PFC中的实现
由于在颗粒流程序中颗粒是刚性的,仅在接触点处产生叠合与错动变形.实际粗颗粒是多棱角的,接触点易被侵蚀破碎,而颗粒本身变形较小;因此,可认为点-面接触试验中,测得的接触力和位移皆是接触点侵蚀造成的.本研究认为,通过颗粒接触试验测得接触力和位移,推导刚度参数,直接作为数值模拟的接触参数,并利用物理试验验证,该方法是可行的.
PFC中的接触模型,其法向与切向刚度在计算中通常是固定不变的.为了使试验得到的粗颗粒湿化接触刚度能够在PFC中实现,对程序进行二次开发.通过编写Fish语言,在计算过程中法向与切向接触刚度能够不断调整,使得非线性湿化接触刚度能够在软件中实现.
接触点的法向刚度为
其中,Fn和Un分别为法向力和法向位移.代入式(1)可得
软件中接触点的法向刚度由接触处的两个单元体(颗粒-颗粒、颗粒-墙体)的刚度计算得到,即
其中,kn,A为接触处第1颗粒的法向刚度;kn,B为接触处第2颗粒或墙体的法向刚度.
当两个刚度相同的颗粒接触时,式(5)可表示为
将式(4)代入式(6),可得
其中,kn,A为颗粒的法向刚度.根据拟合参数a0、b0的数值和湿化折减系数及式(7)可以计算出在PFC程序中颗粒单元的法向刚度(表5).
同理,根据切向接触刚度Ks的定义
假定试验中的切向位移全部是接触点侵蚀造成的,忽略颗粒本身的变形和滑移变形,结合式(2)和式(8)可得
与法向刚度计算规则相同,接触点的切向刚度也是通过两个实体各自的切向刚度计算得到.当颗粒与颗粒接触时,切向刚度可表示为
其中,ks,A为颗粒的切向刚度.
考虑湿化作用时,将式(9)和式(10)联立,可以得到
由式(11)可得颗粒的切向刚度,结果请扫描论文末页右下角二维码查看补充材料表S1.由于法向、切向接触刚度与法向、切向位移有关,通过Fish语言记录数值计算当前的位移值,并通过表S1中的颗粒法向、切向刚度公式计算出下一时刻的颗粒刚度,并重新赋予参数,进行迭代计算,在PFC中实现粗颗粒湿化接触刚度的模拟.
为了与固定刚度进行对比,对图3 和图6 中的刚度曲线进行线性拟合,并确定其固定刚度值,结果请扫描论文末页右下角二维码查看补充材料表S2.其中,kn,dry、kn,wet和kn,sat分别代表自然风干、表面润湿和浸泡状态的颗粒法向刚度;ks,dry、ks,wet和ks,sat分别代表自然风干、表面润湿和浸泡状态的颗粒切向刚度.
4 大型直剪验证试验
为验证本研究所建立的粗颗粒湿化接触经验模型及参数的适用性,对复杂湿化状态下的石灰岩碎石颗粒进行大型湿化剪切试验,并建立离散元数值模型,验证湿化接触经验模型的可靠性.
4.1 试验设备及湿化改造
试验采用大型直剪仪,请扫描论文末页右下角二维码查看补充材料图S1.剪切盒尺寸为400 mm× 400 mm × 410 mm,壁厚为30 mm.最大竖向压力为200 kN,最大水平拉力为500 kN,最大位移量程为120 mm,最大采样频率为1 Hz.
为了与粗颗粒湿化接触试验相对应,使用保鲜膜缠绕上下剪切盒之间的缝隙,对直剪盒进行密封.同时,连接加湿器向剪切盒内通入水蒸气进行加湿.当从剪切盒顶部观察到试件表面颜色呈深灰色,颗粒表面分布较多水珠并流下,此时视为试样整体均已达到表面润湿状态.根据试做试验,最终确定以1 500 mL/h 出雾量加湿12 min,湿化程度达到试验要求.对于浸泡状态,与粗颗粒湿化接触试验一致,试验开始前将试件提前浸泡60 min.对于自然风干试样,无需做加湿处理.
与颗粒接触试验相对应,大型直剪试验所用石灰岩碎石土过标准筛,保留粒径在2~5 cm 内较大颗粒为主要研究对象,其干密度为1.875 g/cm3,相对密实度为0.8,不均匀系数和曲率系数分别为1.662和0.962.
4.2 试验内容及分组
根据湿化状态和法向压力的不同,大型湿化剪切试验共分为9 组,见表4.试验前刚性接触面需进行润滑,防止摩擦干扰.分4层装样并压实,装满后静置,确保应力分布均匀.

表4 大型湿化剪切试验分组Table 4 Groups of large wetting shear tests
根据直剪试验规程,通常需剪切至试样边长的15%,即60 mm 时结束试验.直剪盒壁厚仅为30 mm,因此试验前需将下盒反向推进30 mm,再进行试验,使得剪切位移能够达到60 mm以上.
启动设备后,采用静力控制加载方式施加法向压力,以5 kN/min速度加载至目标应力后静置,确保试样内部应力均匀.然后,采用位移控制加载方式施加切向拉力,并以2 mm/min 的速率对试样进行剪切,设置数据采样时间间隔为1.0 s.
4.3 大型湿化剪切验证试验结果分析
图7为石灰岩碎石颗粒的剪切力与累计位移关系曲线.不同湿化状态下的颗粒剪切曲线形态均表现为剪切力随剪切累计位移的增大而增大,且曲线中没有明显的下降阶段.湿化后的碎石颗粒曲线波动更明显,说明湿化对碎石颗粒起润滑和软化作用,导致接触点在剪切过程中更易发生滑移和破碎等现象.

图7 剪切力-累计位移关系曲线(a)自然风干;(b)表面湿润;(c)浸泡Fig.7 Shear force-cumulative displacement curves of (a) air drying,(b) surfaces wetting,and (c) soaking.Black circle,red square,and blue triangle symbolic lines are for Fn=30,60,and 90 kN,respectively.
由剪切力与累计位移关系曲线求得粗粒土的强度参数列于表5.由于石灰岩碎石颗粒的粒径范围为2~5 cm,粒径大且无细粒填充,产生较大假性黏聚力.湿化后的碎石颗粒内摩擦角较自然风干状态时略微增大,假定黏聚力约减小25%.

表5 碎石试样强度参数Table 5 Strength parameters of gravel samples
5 粗颗粒湿化接触模型的验证
5.1 离散元数值建模
选择基于散体介质理论的离散元程序PFC3D,对大型湿化剪切试验进行数值模拟,模型尺寸与大型湿化剪切试验保持一致,如图8,颗粒直径保持在2~5 cm,颗粒数目为1 756颗.

图8 大型湿化剪切试验数值模型Fig.8 Numerical model of large wetting shear test.
为了模拟刚性墙体,墙体的法向刚度取较大值,设为1.0×1020kN/mm.同时,切向刚度定为0,即摩擦系数为0,以模拟大直剪试验润滑后的刚性侧壁.如第4节所述,由于计算中法向和切向刚度都是非线性的,利用Fish语言记录计算过程中的接触位移和法向力,根据补充材料表S1 计算得出新的法向和切向接触刚度,再重新赋予到材料参数中去,通过这种迭代的方式在PFC中实现非线性湿化接触模型.剪切过程中法向应力保持不变,采用位移控制加载,加载速率为2 mm/min,当累计位移达到70 mm时结束数值试验.
5.2 碎石颗粒湿化剪切数值试验结果
根据式(9),可得到不同工况下碎石颗粒大直剪数值试验剪切力与切向位移的关系曲线(图9).为便于对照,同时给出采用固定刚度计算得到的曲线.非线性刚度和固定刚度数值计算的结果见表6.

表6 刚度的数值计算与实测结果Table 6 Numerical calculation and measured results of stiffness

图9 数值试验剪切力-位移关系曲线(a)自然风干;(b)表面湿润;(c)浸泡Fig.9 Shear force-displacement curves in numerical tests of(a) air drying,(b) surface wetting,and (c) soaking.The solid black circle,red square and blue triangle symbolic lines are for nonlinear stiffness of Fn=30,60 and 90 kN,respectively.The hollow symbolic lines are for corresponding fixed stiffness.
由图9可见,数值试验与物理试验的剪切力-剪切位移曲线变化规律基本一致,都属于剪切硬化型曲线,数值试验曲线的波动更加剧烈.
对比图9 和表6 可知,当采用非线性刚度计算时,数值计算和实测得出的剪切强度误差较小,最大相对误差也仅有4.68%;而采用固定刚度计算的误差明显偏大,最大相对误差达到35.3%.因此证明,采用本研究方法对实际石灰岩碎石颗粒进行离散元数值计算是可行的,计算精度满足要求.
6 结论
利用不同湿化程度的石灰岩粗颗粒进行接触试验,总结非线性接触经验模型,并对石灰岩碎石颗粒大型湿化剪切试验进行离散元数值模拟,可得:
1)湿化直接影响粗颗粒点-面接触的破坏形态.湿化使法向接触破坏程度更加严重,锥体颗粒凸起部分逐渐破碎并剥落,其中侧棱部分破碎更加明显;切向接触面积随湿化的加深而增大,立方体颗粒产生更深的划痕,甚至产生较浅的剪切破裂面.
2)不同湿化状态的粗颗粒法向接触刚度曲线形态大致相同.湿化对粗颗粒法向接触刚度产生影响,表现为表面湿润状态的粗颗粒法向接触刚度较自然风干状态时略微减小,而浸泡状态的粗颗粒法向接触刚度较自然风干状态时明显减小.
3)湿化后的法向接触刚度曲线在试验初期与风干态相比差别较小;随后差别不断增大,尤其是浸泡态.表面湿润对于切向接触刚度影响很小;而浸泡的影响较大,切向刚度约降低了20%,吸水后软化对石灰岩颗粒切向接触刚度影响明显.
4)利用湿化接触模型对大型湿化剪切试验进行数值模拟发现,采用固定刚度计算误差较大,最高可达35.3%;而非线性刚度的误差非常小,最高只有4.68%,其计算精度满足要求.
本研究只对颗粒直径范围在2~5 cm 的石灰岩粗颗粒湿化接触性质及接触模型进行了初步探索,受限于颗粒接触试验条件,细观参量的测试存在一定困难,并未对粒径的大小,尤其是小粒径的接触性质进行探究.同时,对于其他岩性,如软岩颗粒的湿化接触性质,仍有待深入研究.
