基于ZigBee的井下巷道人员定位系统
2023-11-21夏书娟苗曙光李晨晨汪徐德
夏书娟,苗曙光,李晨晨,刘 想,张 岳,汪徐德
(淮北师范大学 物理与电子信息学院,安徽 淮北 235000)
长期以来,我国的能源特点是“富煤少气”,煤炭资源约占世界煤炭总资源的11.1%,在国民经济中占有举足轻重的地位[1]。随着煤矿开采的不断深入,环境越来越恶劣,时常会发生瓦斯、煤尘、透水等灾害,井下人员的安全问题备受关注。建设可靠的井下人员定位系统是防范事故发生、减少人员伤亡、提高煤矿事故营救效率的重要保障。随着网络技术智能化的发展,以ZigBee为代表的无线传感器网络(wireless sensor network,WSN)的应用领域越来越广,如军事应用、工厂监测、农业生产、智能家居、医疗护理和煤矿井下等领域。本文设计了基于RSSI算法的井下人员定位系统,在不增加锚节点成本的情况下提出了一种基于卡尔曼滤波的阈值优化算法。该系统优势在于成本能耗低、硬件设备少、抗干扰能力强,能较好地满足煤矿井下场景的需求。
1 定位系统的整体概述
定位系统主要由锚节点、定位装置、协调器和监控管理中心组成,如图1所示。
(1)监控管理中心。监控管理中心主要用于分析协调器发来的各个锚点与人员的位置信息,通过算法计算出人员的具体位置并显示出来。在必要时还可通过监控管理中心找到距离人员最近的锚节点,并下发报警信号。
(2)协调器。协调器主要用于将锚节点发来的数据经过编码打包的方式通过以太网上发给监控管理中心,并在接收到管理中心下发的报警信息时,立即给对应的锚节点发送报警信号。
(3)锚节点。锚节点主要用于接收定位装置发送的请求信号,通过信号强度转化的RSSI值计算出节点与定位人员的距离,并将数据上发给协调器,在接收到报警信息后会立即给定位人员发送报警信号。
(4)定位装置。定位装置主要佩戴在井下人员的身上,通过不断地发送定位请求给锚节点,将自己的具体位置告诉监控管理中心。在接收到锚节点发送的报警信号后会立即通过声光报警装置发出报警提醒人员。

图1 井下ZigBee定位系统框图
2 定位节点设计
2.1 系统工作流程
系统以CC2530作为锚节点、人员定位装置、协调器的主控。将锚节点安装在井下隧道旁,当携有定位装置的人员经过时,定位装置会向附近的锚节点发送请求信号,接着锚节点会把接收到的信号强度转化为距离值,并通过多跳的传输方式进行逐级传递,使距离信息汇总至协调器,再由协调器借助以太网上传到井上的监控管理中心。监控管理中心通过处理各个节点与定位人员的距离,利用加权质心定位算法计算出人员位置,并显示出来。总体流程如图2所示。
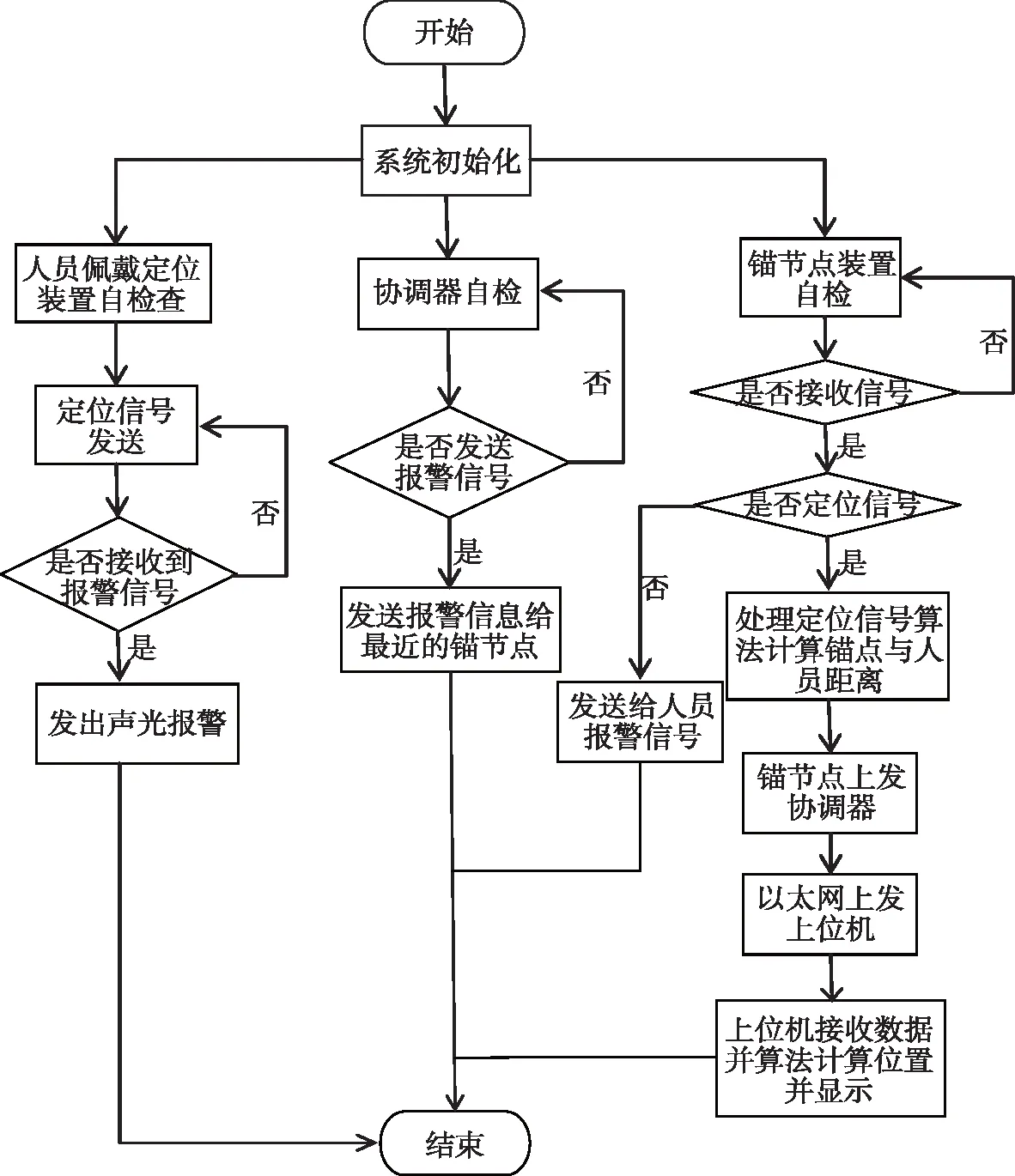
图2 总体流程图
2.2 系统资源介绍
主要用到的硬件资源:电源模块、CC2530单片机、无线通信模块、 声光报警和OLED显示模块,如图3所示。
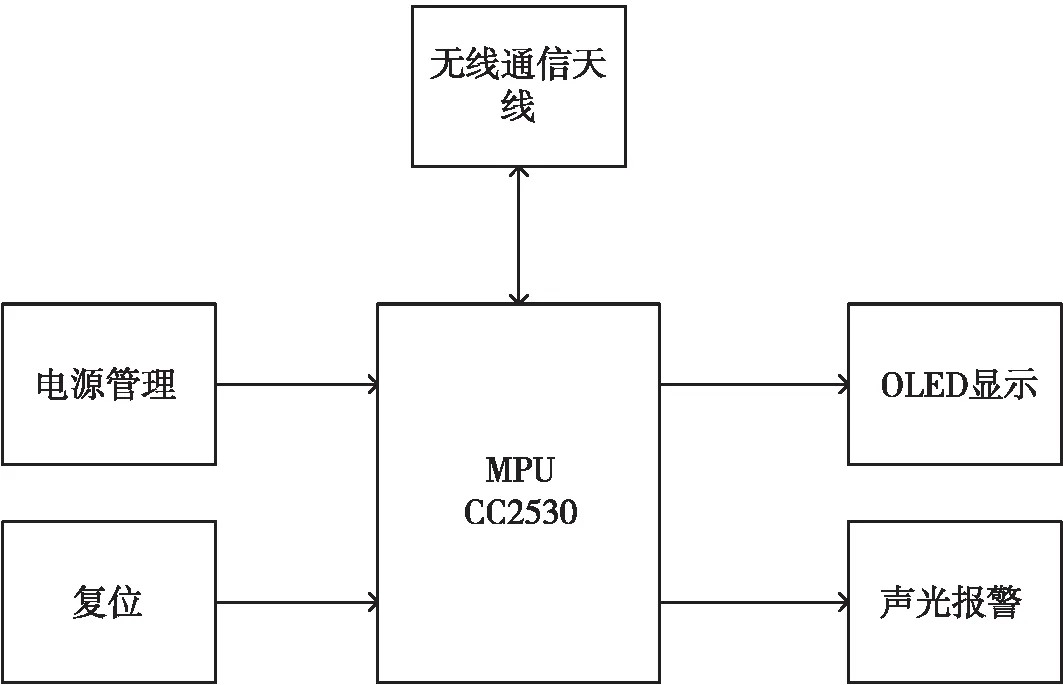
图3 定位节点组成框图
(1)电源模块:为定位节点提供电源,CC2530单片机工作电压一般处于2.6 ~ 3.6 V,为保障单片机以及其他模块的正常工作,选用了3.3 V稳压芯片作为系统供电模块。
(2)CC2530单片机:由TI公司生产,用于ZigBee的片上系统[2],芯片结合了ZigBee协议栈,具有中断、定时器、看门狗、串口、高精度ADC、DMA等多种功能外设,在本设计中通过使用内部12位高精度ADC采集信号强度并转化为RSSI;将RSSI值通过算法计算得到距离信息并存储在CC2530的Flash中;CC2530拥有高性能的RF收发器和增强型的8051微处理器[3],具有信号无线传输、数据分析处理等功能。
(3)RF天线接口:用于增强信号定向式传输和信号接收,通过天线接收人员定位装置发出请求信号,计算RSSI进一步转化为距离信息,再发送给协调器。
(4)声光报警:通过在监控管理平台给人员下发报警信号,人员定位装置接收到报警信号会立即通过声光的方式实现报警。
(5)OLED显示模块:通过OLED显示电源电量,人员定位装置可以显示人员所处位置,在接收到报警信号后可以显示报警信息。
3 定位系统的关键技术
井下工作面人员定位系统关键的定位技术主要包括:RSSI测距算法、卡尔曼滤波算法、加权质心定位算法。
3.1 RSSI测距
采用对数-距离损耗模型,利用信号值的损耗来计算信号传播的距离[4]:
(1)
将RSSI值转化为距离:
(2)
式中:d(d′)是收发端之间的距离;d0是锚节点间的参考距离;RSSI(d)表示锚节点接收到的强度值;RSSI(d0)表示理想环境下信号传输距离为d0时锚节点接收到的强度值;n为路径损耗系数;wσ是服从零均值高斯分布的随机变量[5]。
3.2 卡尔曼滤波算法
由于信号环境等干扰因素,采集到的RSSI值中含有大量噪声,采用卡尔曼滤波进行除噪处理,将RSSI值中的突变或异常数据滤除。将采集到的信号值输入到以下系统方程中,通过预测和更新,得到下一时刻的状态准确值。
状态方程:Xk=AXk-1+BUk+Wk
观测方程:Zk=HXk+Vk
式中:Xk是滤波后k时刻的RSSI值;A为状态转移矩阵,表示预测过程,取1;B为控制矩阵,取0;Uk称为控制输入向量;Zk是k时刻测量的RSSI值;H表示从状态量到观测的转换矩阵取1;Wk和Vk分别表示过程和测量噪声,均为高斯白噪声[6]。
卡尔曼滤波基本迭代过程:
(1)向前推算状态变量:基于上一时刻(k-1时刻)的最优估计值预测k时刻的先验估计,并加上外部控制量的修正。
X(k|k-1)=AX(k-1|k-1)+BUk
(3)
式中:X(k-1|k-1)是上一时刻的最优结果[7];X(k|k-1)是k时刻的结果。
(2)向前推算误差协方差:基于上一时刻(k-1时刻)的不确定性(后验估计协方差)预测k时刻的先验估计协方差,并加上外部环境的干扰。
P(k|k-1)=AP(k-1|k-1)AT+Q
(4)
式中:P(k|k-1)是X(k|k-1)的协方差;P(k-1|k-1)是X(k-1|k-1)的协方差;Q是Wk(过程噪声)的协方差[7]。
(3)计算卡尔曼增益:基于预测部分和测量部分的两个高斯分布的结合。
K=P(k|k-1)HT(HP(k|k-1)HT+R)-1
(5)
式中:R是Vk(测量噪声)的协方差,一般可以观测到,是已知条件。
(4)观测变量更新估计:预测和测量的残差结合卡尔曼增益一起修正预测,得到最优估算X(k|k)。
X(k|k)=X(k|k-1)+K(Zk-HX(k|k-1))
(6)
(5)更新测量协方差:
P(k|k)=P(k|k-1)-KHP(k|k-1)
(7)
这是卡尔曼算法的一次滤波过程,如图4所示,X(k|k)为新的最优估计,将X(k|k)和P(k|k)放到下一个预测和更新方程中不断迭代。

图4 卡尔曼滤波算法过程图
3.3 改进的基于RSSI测距算法
对通过卡尔曼滤波处理后的RSSI值从小到大进行排列,即RSSI,1≤RSSI,2≤RSSI,3≤…≤RSSI,n,确定其中位数MRSS:
(8)
由于中位值附近误差信号影响,在中位数中增加一个阈值,用于优化RSSI值。取值方法:不同RSSI值分别与中值求差,将差值平方求和,取平均值即阈值:
Ti=(RSSI,i-MRSS)2
(9)
(10)
接着使用误差的阈值对权值进行优化:若某个RSSI值位数之差的平方(方差)小于阈值,则权值由阈值(Tavg)决定[8];若方差大于阈值,则权值由方差(Ti)决定。RSSI测量值的权值定义:
(11)
将该组的每个RSSI值分别与对应的权值相乘再求和,得到最终的RSSI值。
(12)
3.4 三角形加权质心定位算法
三角形状加权质心定位算法在质心算法的基础上通过给每个锚节点分配不同权值的方法,进一步提高定位精度,即锚节点离未知节点越远其权值越小[9-10]。设未知节点到锚节点的距离分别为dai、dbi、dci。
第i个未知节点O估计坐标为(xi,yi),计算公式:
(13)
4 仿真结果与分析
为了验证改进算法的性能,使用Matlab软件进行仿真实验,选定区域为在100 m × 5 m的区域,将20个锚节点均匀分布在区域长边框,以此来模拟井下巷道。设路径损耗因子为5,通信半径为10 m,进行仿真实验50次,取结果的平均值。当锚节点为20个时,将实际值、质心定位、加权质心定位估计值进行对比,仿真结果如图5和6所示。
卡尔莫滤波改进后的加权质心算法的定位误差明显小于质心定位的算法误差。质心定位的最大定位误差距离为4.3 m,集中分布在1~3.2 m,平均定位误差在2.047 m;加权质心算法的最大定位误差距离为1.8 m,集中分布在0.3~1.5 m,平均定位误差在0.594 m,定位精度提高了70%左右。为了评估锚节点密度对质心定位算法和加权质心定位算法的影响,增加一组锚节点为40个进行仿真如图7和图8所示。质心定位受锚节点数量影响较大,在40个锚节点情况下,平均定位误差为1.27 m;加权质心定位受锚节点数量影响较小,平均定位误差为0.539 m。
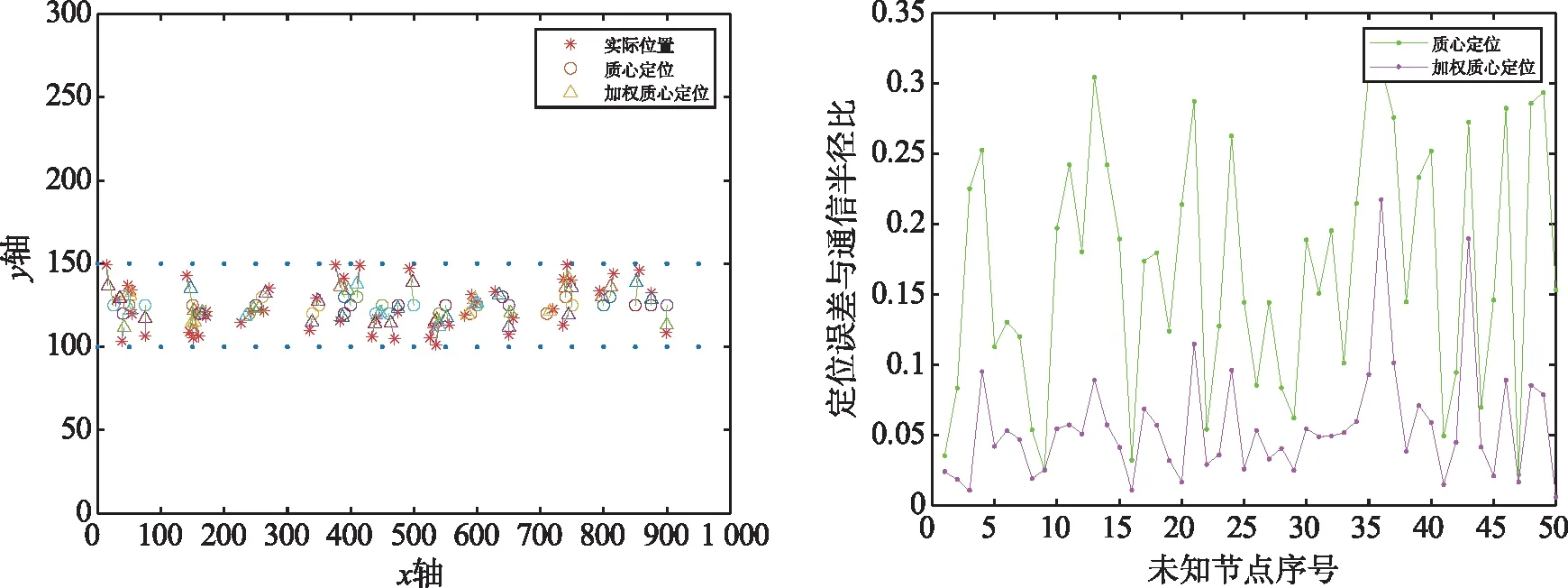
图7 锚节点为40个时的定位坐标 图8 定位误差
5 结 语
对ZigBee的井下人员定位系统进行了研究与设计,系统以CC2530作为主控芯片,实现了井下人员的实时定位与监控。针对RSSI信号容易受到噪声、多径传播、障碍物阻挡等影响,且在计算过程中存在信息丢失的问题,提出了一种基于卡尔曼滤波的阈值优化算法。相较于传统的质心定位算法,改进后的定位算法减小了定位误差,明显提升了定位精度,且不依赖于锚节点的数量,有效缩减了锚节点的硬件成本,同时也提高了定位的相对稳定性。
