低速重载风电齿轮箱径向滑动轴承多运行状态润滑性能分析
2023-11-21赵帅可苏华
赵帅可, 苏华
(西北工业大学 机电学院, 陕西 西安 710072)
风力发电有望成为未来绿色能源的主要来源,风电齿轮箱作为风力发电设备的主要装置,有着巨大的科研价值和市场潜力。传统的风电齿轮箱广泛使用滚动轴承作为传动装置支承,但是滚动轴承因传递扭矩小、承载力小、故障率高等问题无法满足风力发电机大功率、高承载力的发展需求。因此,研制能够满足大传递扭矩、大承载力、高稳定性且制造成本低的支承系统十分迫切。与滚动轴承相比,滑动轴承具有高承载力和高稳定性的优势,因此以滑动轴承部分取代传统风电齿轮箱中的滚动轴承,是未来风电齿轮箱传动系统支承的一种可行方案和研究趋势。
由于风力和风向变化的随机性,风电齿轮箱滑动轴承具有启动频繁、载荷大小和方向多变、低速重载等运行特点。
频繁启停和变载使得轴承更容易发生破膜,因此研究启动工况下风电齿轮箱中径向滑动轴承的润滑特性十分重要。国内外已有不少学者开展了径向滑动轴承启动过程中润滑性能的研究,如Liang等[1]将欧拉方程、平均Reynolds方程耦合起来,建立了水润滑径向滑动轴承启动模型,研究了冲击载荷对于轴承系统稳定性的影响;Chen等[2]将非理想轴颈的瞬态混合润滑模型与轴颈运动方程耦合,研究了水润滑轴承启动过程中轴颈缺陷对其摩擦动力学行为的影响;Li等[3]通过试验的方法测得了不同工况下滑动轴承的摩擦因数和磨损量,并指出启动工况下轴承的磨损量和摩擦因数远大于稳态工况;Cui等[4]研究了不同表面粗糙度对轴颈中心瞬态运动、瞬态平均油膜厚度、动水压力和接触压力的影响,指出表面粗糙度对轴承启动初期的瞬态特性有重要影响。
风电机组的服役工况比较恶劣,常年在低速、重载的工况下运行,较难形成稳定的动压油膜,频繁的变载冲击会使滑动轴承中的油膜容易发生破裂造成轴径/轴瓦粗糙表面接触,且偏航力矩所造成的轴颈倾斜也会对滑动轴承的性能产生较大影响。因此研究风电齿轮箱中的径向滑动轴承性能时,还必须综合考虑表面粗糙效应、轴颈倾斜以及转速等变化对轴承性能的影响。目前,国内外很多学者对考虑粗糙表面和轴颈倾斜的径向滑动轴承开展了相关研究。如Sun等[5-6]通过理论和试验的方法研究了粗糙表面滑动轴承在轴颈受载倾斜时的润滑性能,指出在滑动轴承设计中应考虑轴颈变形倾斜所产生的影响;Sander等[7]基于平均Reynolds方程研究了径向滑动轴承从流体动力润滑状态到混合润滑状态下的摩擦行为,通过2种不同静载荷的摩擦试验,指出了表面粗糙度对微凸体接触和摩擦力矩的影响不可忽视;李彪等[8]基于平均Reynolds方程,建立了考虑粗糙表面径向滑动轴承润滑模型,探究了滑动轴承中表面形貌和轴颈倾斜对轴承润滑特性的影响规律,指出在对轴承润滑性能分析时不能忽略表面形貌的影响。上述研究一般仅考虑了稳态条件下的轴承性能,很少涉及启动等瞬态阶段。
可以看出,目前针对瞬态或稳态条件下的滑动轴承性能研究基本上是各自独立进行的,瞬态和稳态耦合的相关研究鲜有报道。但是对于风电齿轮箱滑动轴承而言,频繁的启动和多变载荷工况下的性能稳定性必须同时考虑。本文基于平均Reynolds方程,提出一种将滑动轴承启动瞬态润滑工况和稳态润滑工况耦合起来的性能分析方法,分析由启动阶段至稳态工况的轴心运动轨迹以及不同作用角下轴承润滑油膜厚度、承载力的分布情况;研究表面粗糙度、轴颈倾斜角度和轴颈转速对启动阶段和稳态工况下滑动轴承润滑性能参数的影响,以获得风电齿轮箱滑动轴承从启动至稳定运行的整体运行润滑特征。
1 几何模型
本文研究的风电齿轮箱滑动轴承结构如图1所示,在偏航力矩作用下轴颈会发生倾斜。其中,γ为轴颈倾斜角度;L为轴承宽度;R为轴承半径;r为轴颈半径;δ为外载荷作用角;c1为轴颈在轴承左端面时的中心;c2为轴颈在轴承右端面时的中心。

图1 轴颈倾斜示意图
本文径向滑动轴承的结构及工况参数如表1所示。

表1 径向滑动轴承结构及工况参数
2 数值分析方法
2.1 数值计算模型
1) 润滑油膜厚度[9]
滑动轴承内任一点油膜厚度h为
(1)
式中:e为偏心距(不同y方向截面处偏心距不同,倾斜角度由x,y坐标进行控制);θ为轴承周向坐标;φ为作用角;c为半径间隙;x为轴颈中心在y方向(轴向方向)不同位置的坐标值(x1,x2分别为轴承左右端面坐标值);z为轴颈中心在y方向(轴向方向)不同位置的坐标值(z1,z2分别为轴承左右端面坐标值)。
2) 平均Reynolds方程[10]
本文基于平均Reynolds方程计算油膜压力

求解时采用以下边界条件:
端泄面处:p(θ,0)=p(θ,L)=0
油膜压力起始点:p(θ,y)=0
3) 能量方程[11]
设本文所研究的滑动轴承为均匀、各向同性材料,其导热系数、比热、密度均为常数,系统内无热源,可采用能量方程
(4)
式中:ρ为润滑油密度;cρ为润滑油比热;T为温度;U为流体在x方向上的速度分量;k为润滑油热传导系数;p为压力;J为热功当量;qx为x方向的流量;qy为y方向的流量。
能量方程的边界条件为:
温度起始点:T|θ=0=T|θ=2π
4) 温黏方程
对于重载和流体动压润滑,本文采用更加准确的Roelands表达式[12]来考虑温度和压力变化对黏度的影响
η=η0exp{(lnη0+9.67)·
(5)
式中:η0为润滑油在初始温度T0时的黏度。
5) 微凸体接触模型
对于油膜润滑,在考虑干摩擦接触时通过高斯积分得到接触压力与表面粗糙度因素的关系方程式[13]为
(6)
式中
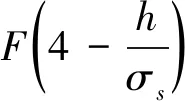
表面粗糙度因素在粗糙度接触区和全润滑区的取值不同:
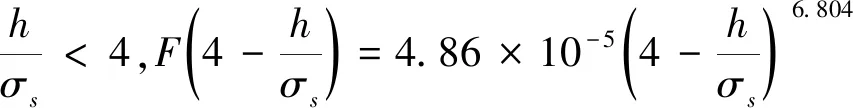

2.2 轴承润滑性能参数计算
1) 油膜承载力[14]
(7)
(8)
(9)
Fx,Fz为油膜反力F在x和z坐标轴方向上的分量,R为径向滑动轴承半径。
2) 摩擦力与摩擦因数[15]
式中:Fj为轴颈表面摩擦力;uj为轴颈表面摩擦因数。
3) 微凸体承载比[16]
本文所研究的微凸体不涉及弹性变形,对于微凸体承载比的计算如(12)式所示
F′为微凸体总承载力;Ro为微凸体承载比。
3 计算流程及程序准确性验证
为了更准确计算出径向滑动轴承的润滑性能参数,本文计算将滑动轴承从启动至稳态运动耦合起来计算,计算流程如图2所示。数值计算流程包括求解启动阶段的滑动轴承润滑性能和进入稳态工况下的滑动轴承润滑性能。首先,轴承启动进入启动阶段,此时采用含有时间项的平均Reynolds方程对压力分布进行计算,进而得出承载力,根据计算得出的承载力对启动阶段的偏心率进行修正,进而得到启动阶段的偏心率随时间t变化的轨迹;当偏心率满足收敛时(如(14)式所示)则进入稳定阶段,进而在稳定阶段定偏心率下求解滑动轴承润滑性能。
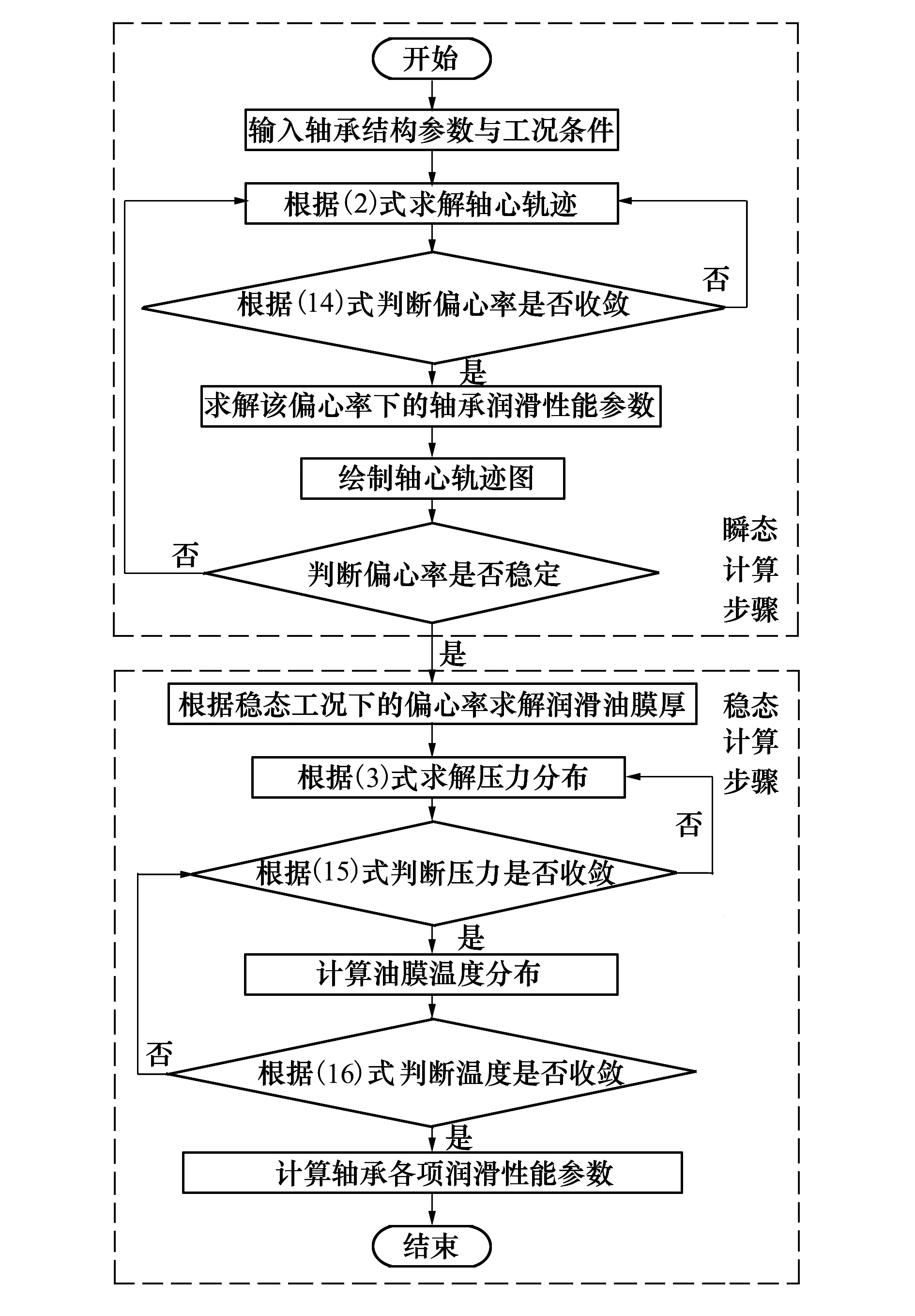
图2 计算流程图
由图2可知,数值计算循环迭代过程中涉及偏心率、压力、温度的收敛性判定。其收敛判断式为:
|εN+1-εN|≤0.001
(14)
(15)
(16)
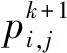
图3为不同倾斜角度下本文模型求解得到最大油膜压力与文献[8]中稳态工况下最大油膜压力的计算结果对比情况。文献[8]中轴承参数如表2所示。

表2 文献[8]轴承工况

图3 本文计算结果与文献[8]结果对比图
可以看出,本文润滑模型的计算结果与文献[8]中的计算结果具有高度的一致性,验证了本文计算模型和算法的正确性。
4 轴承润滑性能分析
4.1 启动阶段至稳态轴心轨迹及润滑性能
图4为初始偏心率在0.6和0.8时,表面综合粗糙度取0.8 μm、无轴颈倾斜的径向滑动轴承从启动至进入稳定运行过程中的润滑性能变化。可以看出, 2种初始偏心率条件下, 随着时间增加,轴颈瞬时偏心率、承载力、摩擦因数均逐渐增大,最小油膜厚度逐渐减小,相关变化趋势在23 s左右时达到极值;在23 s后随着时间进一步增加,偏心率开始缓慢减小、最小膜厚逐渐增大,轴承承载力和摩擦因数则迅速减小,并在44 s左右时,均变为定值,此时意味着径向滑动轴承进入稳定状态。
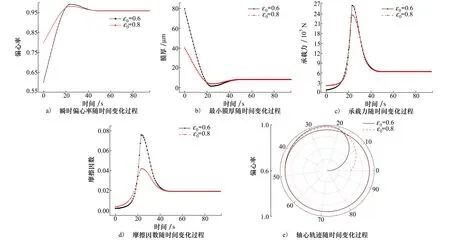
图4 从启动至稳定运行过程中滑动轴承性能变化
在时间为23 s左右时偏心率达到最大值0.996,对应油膜厚度达到最小值约为1.77 μm(如图4b)所示)、对应膜厚比约为2.2,使得轴承表面承载力出现最大值(如图4c)所示),并显著增加轴承摩擦力(如图4d)所示),此时轴承发生大比例粗糙峰接触,油膜破裂风险最高。另外,初始偏心率不同会使轴承的最大偏心率、最小膜厚、最大承载力、最大摩擦因数产生明显差异,但是进入稳定状态后不同初始偏心率对应的轴承性能则趋于一致。因此,选取稳态阶段的偏心率作为本文后续工作的研究工况,即在本文中表面粗糙度、轴颈倾斜角度和转速对滑动轴承性能的影响都是在同一偏心率0.96下进行比较。
4.2 表面综合粗糙度对滑动轴承启动阶段和稳态工况润滑性能的影响
启动阶段和稳态工况下径向滑动轴承的各项润滑性能参数如图5所示。由图5a)和图5b)对比可以看出,启动阶段表面粗糙度对压力影响较大,启动阶段轴向截面压力较稳态工况下的压力高出约96%,这是因为启动阶段偏心率较大,膜厚较稳态下小,因此固体接触更加显著,使得启动阶段压力大于稳态阶段。由图5c)~5d)可以得出,随着表面粗糙度由0.6 μm增长至1.2 μm,启动阶段最小膜厚比由3.54减小至1.77(均处于粗糙接触的破膜风险区),摩擦因数由0.032增加至0.098,微凸体承载比由4.9%增长至24.8%,承载力由2 464 kN增长至2 802 kN;稳态工况下膜厚比由5.06减小至2.53,摩擦因数由0.016增大至0.031,微凸体承载比由2.6%增大至14.6%,承载力由1 869 kN增大至2 242 kN。在表面综合粗糙度为0.8 μm的情况下,启动阶段最大承载力比稳定阶段承载力高出约30.99%,启动阶段最大摩擦因数较稳定阶段摩擦因数高出约131.58%。
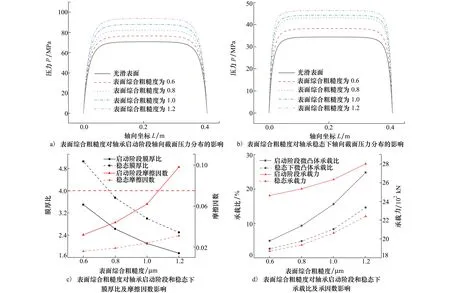
图5 无轴颈倾斜时表面综合粗糙度对轴承润滑性能的影响
4.3 轴颈倾斜角度对滑动轴承启动阶段和稳态工况润滑性能的影响
以图1所示倾斜情况为例,图6为表面综合粗糙度为0.8 μm时轴颈倾斜角度对油膜润滑性能的影响结果,图6a)~6c)稳定状态下为有轴颈倾斜且倾斜角度为0.000 2°的膜厚、压力和温度分布云图,可以看出在接近轴承右端面处(即轴向坐标L为0.41 m处)出现膜厚最小值,此处的固体接触效果更加明显,因此会出现压力最大值(如图6b)所示),同时该处的温升最大(图6c))。由图6d)~6e)可以看出,不论在启动阶段还是稳态工况,轴颈倾斜角度对压力分布的影响规律是一致的,即随着倾斜角度的增大,接近轴承右端压力的最大值增大,且在启动阶段的最大压力约为稳态工况的2倍。由图6f)可以看出,无论启动阶段还是稳定阶段,轴承承载力和摩擦因数均随倾斜角度的增加而增大,且启动阶段的最大承载力和摩擦因数比稳定阶段平均高出约30%和116%。当倾斜角度从0.000 1°增大至0.000 4°,启动阶段承载力由2 464增大至2 974 kN(增大约20%),摩擦因数由0.048增大至0.082(增大约70.83%);稳态工况下,承载力由1 987 kN增大至2 168 kN(增大约9.1%),摩擦因数由0.021增大至0.04(增大约90.48%),可见轴径倾斜对滑动轴承性能有很大影响。
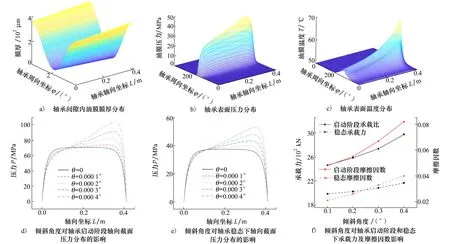
图6 倾斜角度对轴承润滑性能影响
4.4 转速对滑动轴承启动阶段和稳态工况润滑性能的影响
图7为在表面粗糙度为0.8 μm、轴颈倾斜角度为0.000 2°时不同轴颈转速对轴承润滑性能的影响。由图7a)~7b)可以得出,随着转速的增大,启动阶段和稳态工况下的油膜压力都有一定程度增大,且启动阶段的压力明显高于稳定阶段,启动阶段油膜轴向截面压力较稳定阶段油膜轴向压力高出约20%。随着转速的增大,油膜动压效果更加显著,油膜承载力增大,同时由于膜厚不变,油膜摩擦阻力无明显变化,因此摩擦因数呈减小趋势;由图7c)可以看出,随着转速从20 r/min增大至50 r/min,启动阶段承载力由2 184 kN增大至3 068 kN,增大约40.48%,启动阶段摩擦因数由0.046减小至0.031,减小约32.61%;稳态工况下承载力从1 736 kN增大至2 748 kN,增大约58.29%,稳态工况下摩擦因数由0.015 8减小至0.011,减小约30.38%。
5 结 论
基于平均流Reynolds方程,建立滑动轴承的热流体润滑数值模型,计算了风电滑动轴承从启动到稳定过程中的轴心运动轨迹变化,分析了表面综合粗糙度、轴颈倾斜角度和轴颈转速对径向滑动轴承在启动阶段和稳定状态下润滑性能的影响。主要结论如下:
1) 在启动过程中滑动轴承偏心率变化幅度较大,且偏心率的最大值出现在启动阶段。启动阶段膜厚比小于稳态阶段的膜厚比,启动阶段的摩擦因数大于稳态阶段的摩擦因数,故启动阶段出现粗糙接触风险高,轴承的摩擦磨损较大。
2) 表面综合粗糙度对滑动轴承性能有较大影响,当表面综合粗糙度超过0.8后,膜厚比降至3以下、微凸峰承载比显著增加。因此在本文的研究范围内,为了降低不同阶段运行过程中的磨损风险,在满足承载力要求前提下表面综合粗糙度不宜过大。
3) 在本文研究中,轴颈倾斜可以提升油膜的承载能力,但同时也会造成局部干摩擦增大、油膜局部温度过高;摩擦因数的增大使得轴承寿命和润滑性能降低。可以通过适当控制轴颈的倾斜角度来获得更佳的油膜润滑性能。
4) 轴颈转速增大使得轴承的承载力增大,摩擦因数减小;间隙比增大使得轴承的承载力和摩擦因数都减小。因此可以在一定的间隙比下通过适当提升轴颈转速来获得更好的润滑效果。
