基于RBF神经网络的自主水下航行器模型预测路径跟踪控制
2023-11-21郭琳钰高剑焦慧锋宋允轩陈依民潘光
郭琳钰, 高剑, 焦慧锋, 宋允轩, 陈依民, 潘光
(1.西北工业大学 航海学院, 陕西 西安 710072; 2.西北工业大学 无人系统技术研究院, 陕西 西安 710072;3.中国船舶科学研究中心, 江苏 无锡 214082)
自主水下航行(AUV)因其航程远、作业精准度高、可重复使用等特点,成为了人类认识和探索海洋领域必不可缺的工具,在近些年逐渐被广泛应用。精确路径跟踪控制是AUV实现自主航行的关键技术之一,受到国内外学者的广泛关注。
在路径跟踪控制问题上,早期的运动控制方法为比例-积分-微分(PID)控制,文献[1]使用PID控制器实现了路径跟踪,并通过大量的海上实验证明了该控制器的鲁棒性和稳定性。
水下航行器多为欠驱动、强耦合的非线性系统,并受到未建模动态和环境扰动的影响。为提高水下航行器运动控制面对多种不确定因素的鲁棒性,研究人员提出了基于自适应控制[2-4]、滑模控制[5-6]、反步控制[7-8]、神经网络控制[9-10]等路径跟踪控制方案。
Gao等[11]研究了水平面AUV非线性路径跟踪控制问题。以路径上自由参考点为起点的Serret-Frenet坐标来描述路径跟踪误差及其动态方程,解决了经典方法中的奇异性问题。Sun等[12]基于改进的反步法和滑模控制原理,研究了考虑未知环境干扰下的欠驱动水下航行器的路径跟踪控制问题。通过数值仿真验证了滤波反步滑模控制器的控制效果。与传统的反步滑模控制器相比,控制器输出的抖振明显减小,跟踪误差收敛更快,达到稳定跟踪状态所需的时间更短,稳定性更高。然而,AUV水下作业环境复杂,需要考虑各种约束条件,上述控制器难以处理约束问题。
模型预测控制(MPC)是一种基于模型的闭环优化控制策略,相对于传统控制方法的优势在于能够在控制器设计范围内系统地处理带约束条件的多输入多输出问题,目前己经成为了自动控制领域的主流研究方向之一。
在AUV的路径跟踪控制方面,模型预测控制发挥着重要作用。文献[13]考虑了有输入约束条件下的欠驱动AUV直线路径跟踪问题,提出了基于MPC的AUV路径跟踪控制器,并比较了线性预测模型、时变线性预测模型和非线性预测模型的方案,结果表明3种方案均具有良好的跟踪性能和鲁棒性。文献[14]针对含障碍物的受限工作空间,提出了一种新型非线性模型预测控制方案,引导AUV朝着特定方向前进,并在控制器设计中考虑了各种约束条件(如:障碍物位置、工作空间边界、推进器饱和速度限制等)。Shen等[15]针对AUV轨迹跟踪问题提出了基于李雅普诺夫稳定性的模型预测控制(LMPC)框架,在LMPC框架中考虑了驱动器饱和、推力分配等实际性的约束问题。Gao等[16]针对全驱动水下航行器的视角约束、执行器约束和模型不确定性,提出了一种基于滑动模态观测器的模型预测控制策略。刘昌鑫等[17]针对欠驱动AUV的约束路径跟踪问题,设计了一种MPC路径跟踪控制器,采用REMUS AUV的模型参数对提出的控制律进行了仿真研究,实验结果表明控制器在显式处理约束的同时,表现出良好的跟踪效果。在文献[15]的基础上,Shen等[18]研究了AUV的路径跟踪问题,将路径跟踪作为首要任务优先完成,提出了一种新的多目标模型预测控制框架。
MPC控制策略能处理多输入多输出并带约束的复杂系统,且具有较强的可靠性和鲁棒性。MPC优异的控制效果依赖于精确的模型,但是AUV模型具有多自由度、非线性、强耦合性的特点,而且AUV运动数学模型中的部分水动力附加质量、惯性矩和阻尼系数是难以精确建模的。另外,AUV在航行过程中,经常会受到外界(如:未知深层流和表面流)的干扰,上述特点使得AUV路径跟踪控制增添了许多不确定性。
径向基(RBF)神经网络能快速逼近系统动力学模型,结构更简单,与其他神经网络算法相比,RBF神经网络在解决实时函数逼近问题上有一定的优势。因此,本文针对AUV的模型不确定性引入RBF神经网络算法,通过提升预测模型的精度进而优化路径跟踪控制效果。
1 欠驱动AUV数学模型
针对AUV的路径跟踪控制问题,首要工作是建立AUV的数学模型。本文研究水平面上的欠驱动AUV路径跟踪控制问题,为了方便后续的研究分析,忽略欠驱动AUV水平面运动和垂直面运动带来的耦合效应,忽略动力学模型中的非线性二次阻尼项,建立欠驱动AUV的水平面三自由度运动方程。
通常使用2个坐标系来描述AUV的运动(如图1所示):地面坐标系和运载体坐标系。地面坐标系的原点O固定在地球上一处,规定OX向北为正,OY向东为正。运载体坐标系的原点OB选择在AUV的浮心,规定OBXB沿着AUV的纵轴并指向艏向,OBYB与之垂直,向右为正。
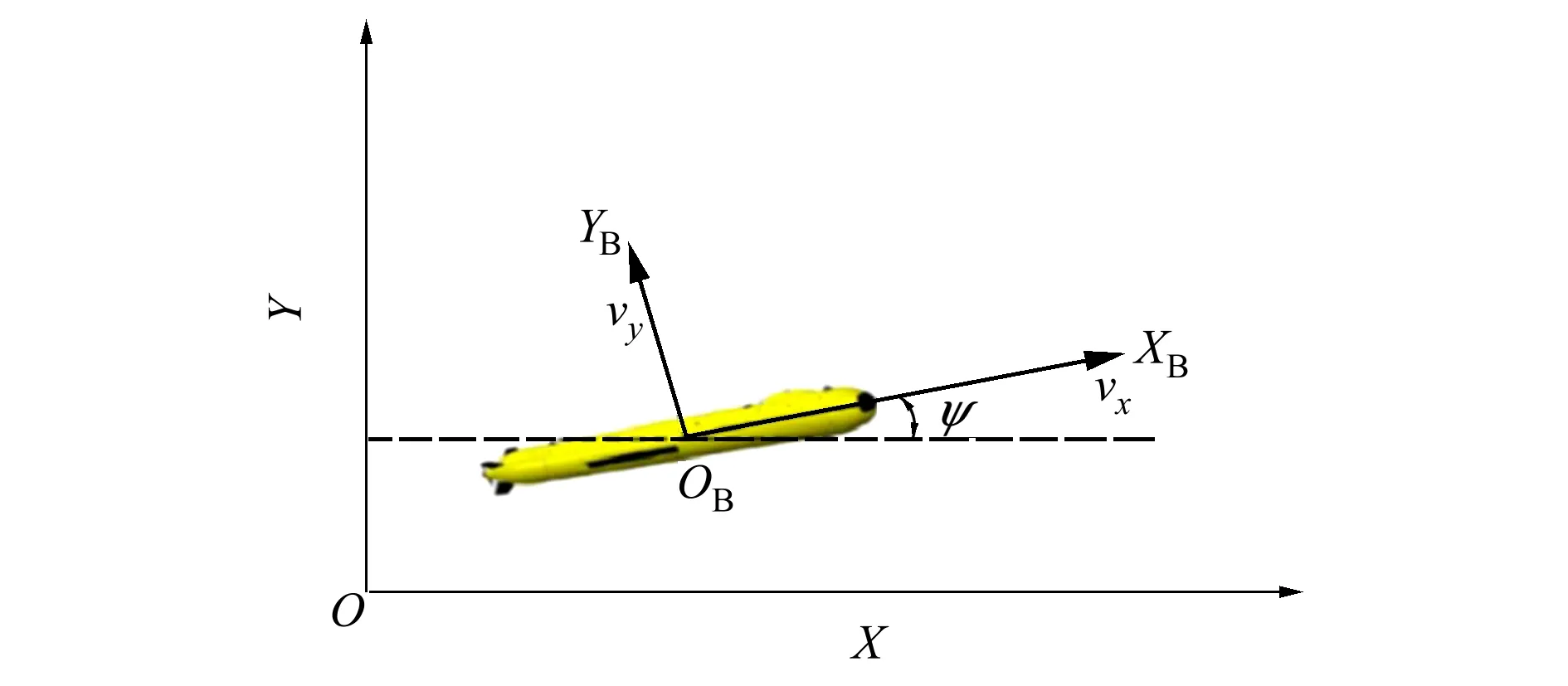
图1 AUV水平面坐标系
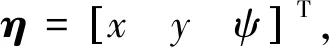
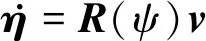
(1)
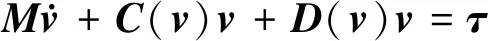
(2)
式中:M为含附加质量的惯性矩阵;C(v)为哥氏力和向心力矩阵;D(v)为阻尼矩阵;τ是在3个自由度上的输入力、推进器产生的推力以及操纵面产生的操纵力。
在(1)~(2)式中,AUV的质量、水动力附加质量、惯性矩和阻尼系数等通常随工作条件(包括任务和环境)的变化而变化,在实践中难以确定。此外,海洋环境扰动往往是不可预测的、多变的。因此,AUV的运动数学模型受到诸多不确定因素的影响。
假设AUV的纵剖面、横剖面分别对称,有
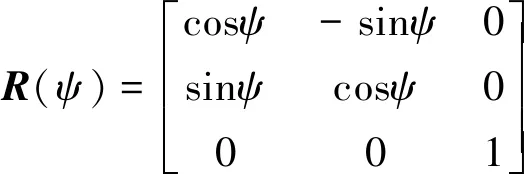
(3)
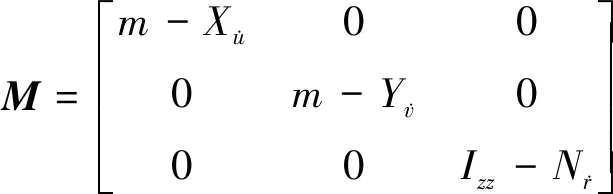
(4)
(5)
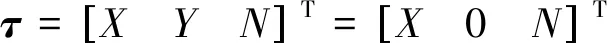
(6)
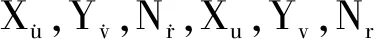
由此可得,欠驱动AUV在水平面上的运动学方程和动力学方程,分别表示为
(7)
和
(8)
式中:m11=M11,m22=M22,m33=M33,d11=D11,d22=D22,d33=D33。
2 RBF-MPC路径跟踪控制器设计
令向量x表示AUV的状态,u表示控制输入,则AUV的状态更新方程描述为
xk+1=f(xk,uk)
(9)
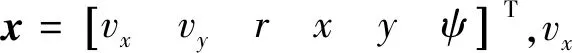
由于AUV模型中参数的不确定性,令Δf(xk,uk)表示AUV模型中的不确定项,fnom(xk,uk)表示名义模型,则真实系统ftrue(xk,uk)表示为
xk+1=fnom(xk,uk)+Δf(xk,uk)=ftrue(xk,uk)
(10)
因此可以将AUV路径跟踪控制问题描述为以下带约束的动态优化问题
(11)
满足
xk+1=fnom(xk,uk)+Δf(xk,uk)
(12)
e(k+1)=xk+1-xref
(13)
umin≤uk≤umax,k=1,…,Nc
(14)
x0=xk
(15)
式中:R和Q分别为路径跟踪状态偏差的权重矩阵和控制输入权重矩阵,(12)式表示不断更新的AUV模型;(13)式中xk+1表示补偿后模型的6个状态;xref是参考状态;u为控制输入力X和力矩N;(15)式中模型预测的初始状态x0为真实系统的当前状态xk反馈。
MPC控制器在AUV进行路径跟踪时通过传感器获得当前时刻的AUV状态值;然后根据预测模型对AUV在预测时域内的状态值进行预测,通过构建目标函数(11)式并结合约束条件(12)式和(14)式优化求解预测时域内的控制序列;最后选取求解得到控制序列的第一个元素作为系统的控制输入。这一时刻结束后在下一个采样时刻重新获取AUV的状态,继续下一周期的滚动优化。
在实际航行过程中,AUV的结构参数经常发生变化。除此之外,由于水下航行器系统的强非线性和强耦合性,也导致AUV实际上难以建立精确的实际系统模型,影响了其跟踪的预设路径的精度。因此,针对模型不确定项Δf(xk,uk),采用RBF神经网络来进行逼近。
RBF网络结构如图2所示,该结构包括3个不同的层,其中n是输入层节点的个数,m是隐藏层节点的个数,l是输出层节点的个数。
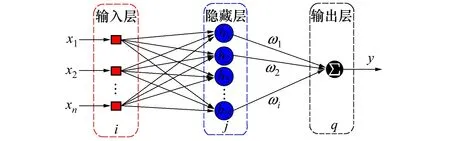
图2 RBF网络原理图
该结构中第一层是输入层,输入层X=[xi]T,其目的是将n个输入分配给第二层隐藏层的m个节点,隐藏层输出H=[hj]T,其中x和hj分别是系统输入和隐藏层的第j个输出,本文选择高斯函数作为激活函数,即
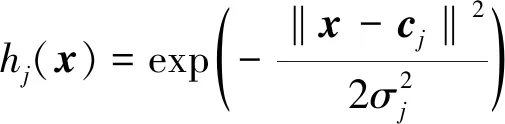
(16)
式中,‖x-cj‖表示x和cj之间的欧几里得距离,RBF神经网络采用中心cj和宽度σj为参数的高斯基函数。
RBF第三层输出层为网络的输出,通过线性组合隐藏层来计算网络的预测输出,从而有计算方式
(17)
式中,wjq是第j个隐藏层节点到第q个输出层节点的权重,采用梯度下降法辨识wjq。
结合(17)式,AUV模型不确定性可表示为
Δf(xk,uk)=WTH(xk)+ε
(18)
式中:W是隐藏层到输出层的权重矩阵;H是由(16)式计算得到的向量;ε是偏差项。权重矩阵W和H分别为m×l和m×1的矩阵,m和l分别表示输入层、隐藏层和输出层的节点数量。
3 仿真实验与结果分析
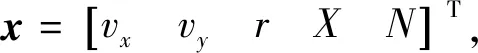
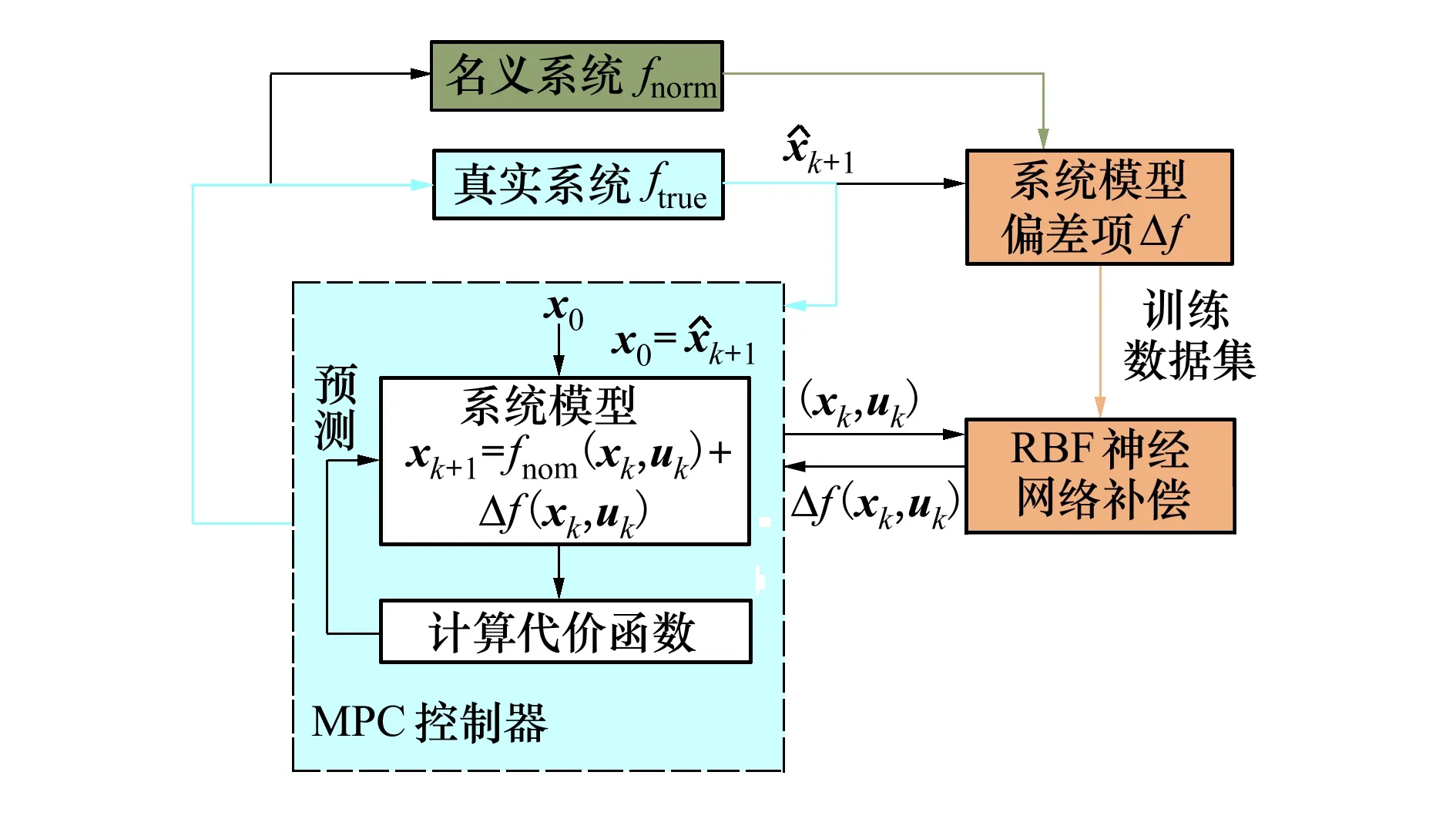
图3 RBF-MPC结构图
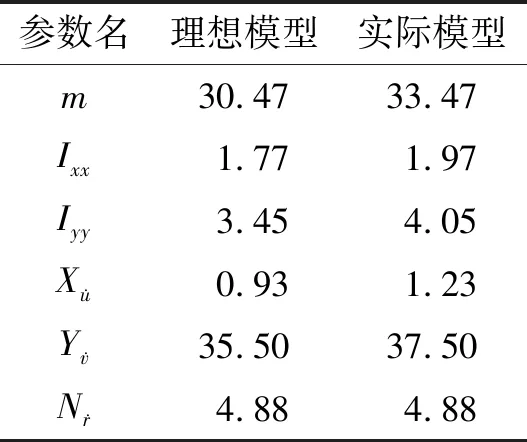
表1 模型参数表
3.1 波形曲线跟踪结果分析
为验证基于RBF-MPC的路径跟踪控制方法的有效性,先将参考路径选择为波形图进行测试,波形表达式选择为
yl=6sin(0.05xl)
(19)
式中:xl为目标横坐标;yl为目标纵坐标。
AUV的初始位置为(0 m,0 m),初始航向角为0 rad,控制器的采样间隔为T=0.1,预测步长为N=50,仿真时间为150 s。跟踪波形的仿真结果如图4~6所示。
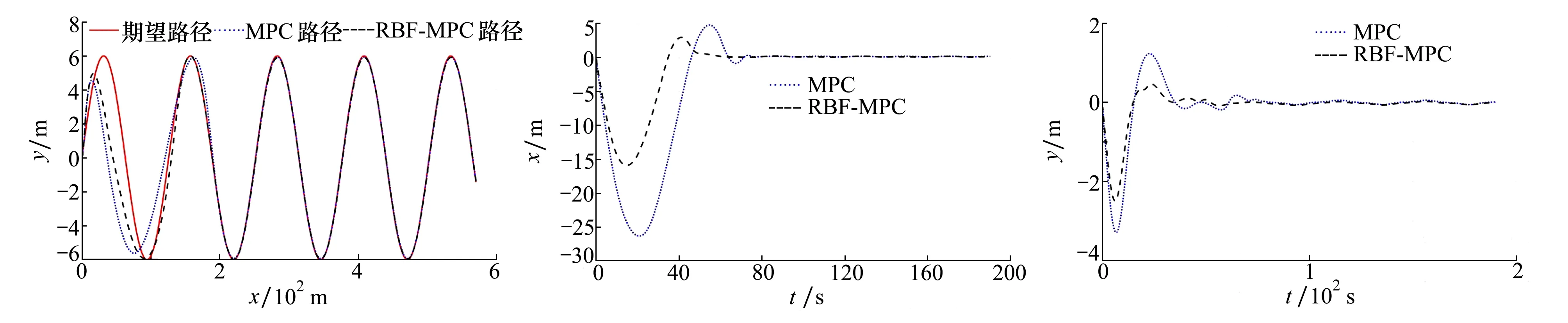
图4 波形跟踪控制结果 图5 x方向跟踪误差对比 图6 y方向跟踪误差对比
从图4可以明显看出,采用RBF神经网络的MPC控制器明显误差更小一些,在横向100 m以内即可跟踪上波形,不仅收敛速度更快,而且横纵位置的偏差更小;而MPC控制器在横坐标大约为180 m处才能在一定误差内跟踪上波形。
为进一步清晰看出MPC控制器和RBF-MPC控制器的跟踪效果差异,将横纵向位置的跟踪偏差结果展示在图5~6。MPC控制器在x方向达到稳态的时间大致为72 s,位置偏差最高可达26.0 m;而RBF-MPC控制器x方向达到稳态时间缩短为大约50 s, 位置偏差减少到13.0 m,位置误差减少大约50%。 因此,在控制器参数、AUV模型和初始状态等其他条件均相同的情况下,RBF-MPC控制器收敛速度更快,超调量更小。
图7~8展示了使用MPC控制器和RBF-MPC控制器跟踪正弦波时,控制输入力和力矩的变化。
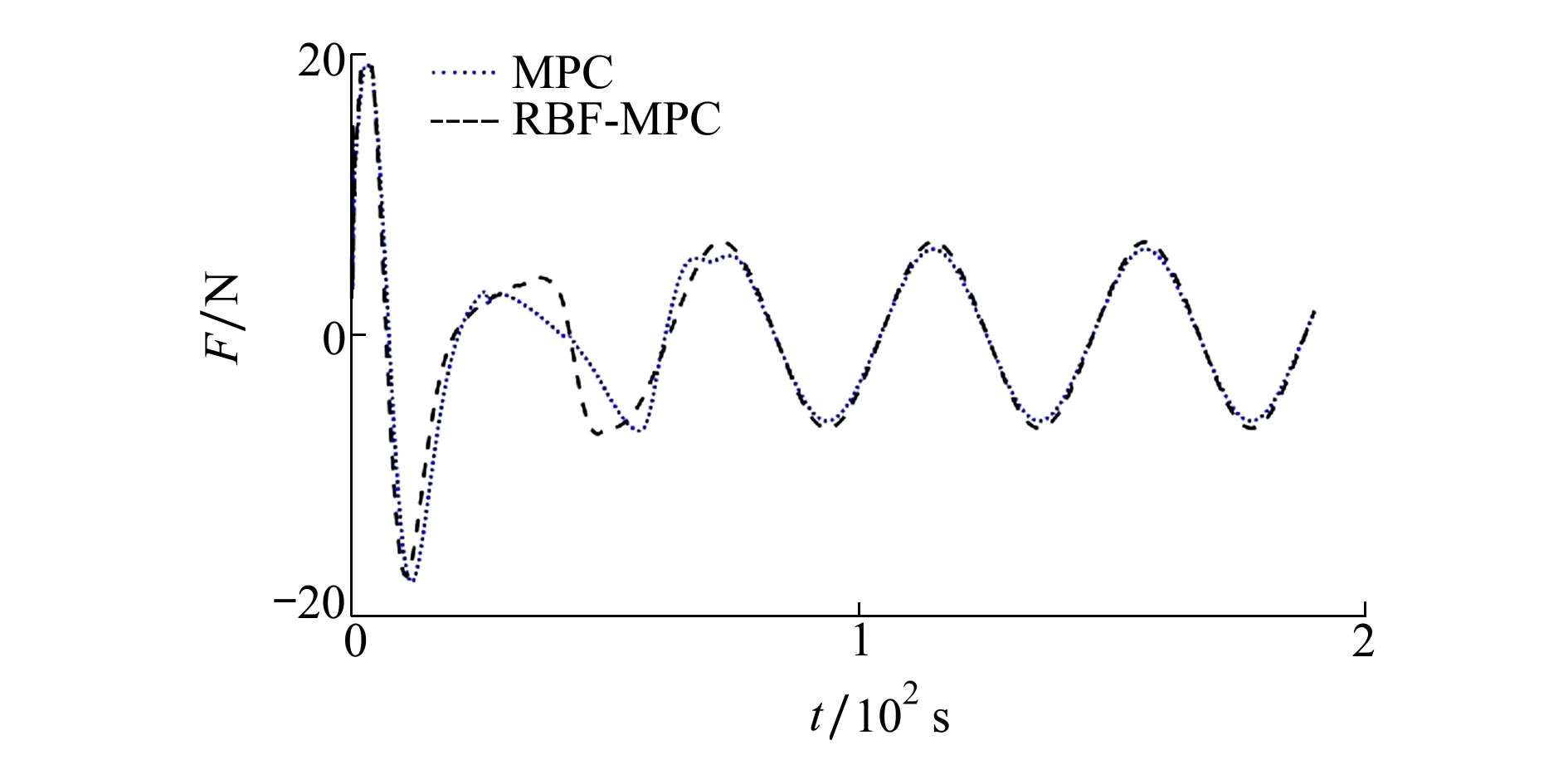
图7 控制输入力的变化曲线
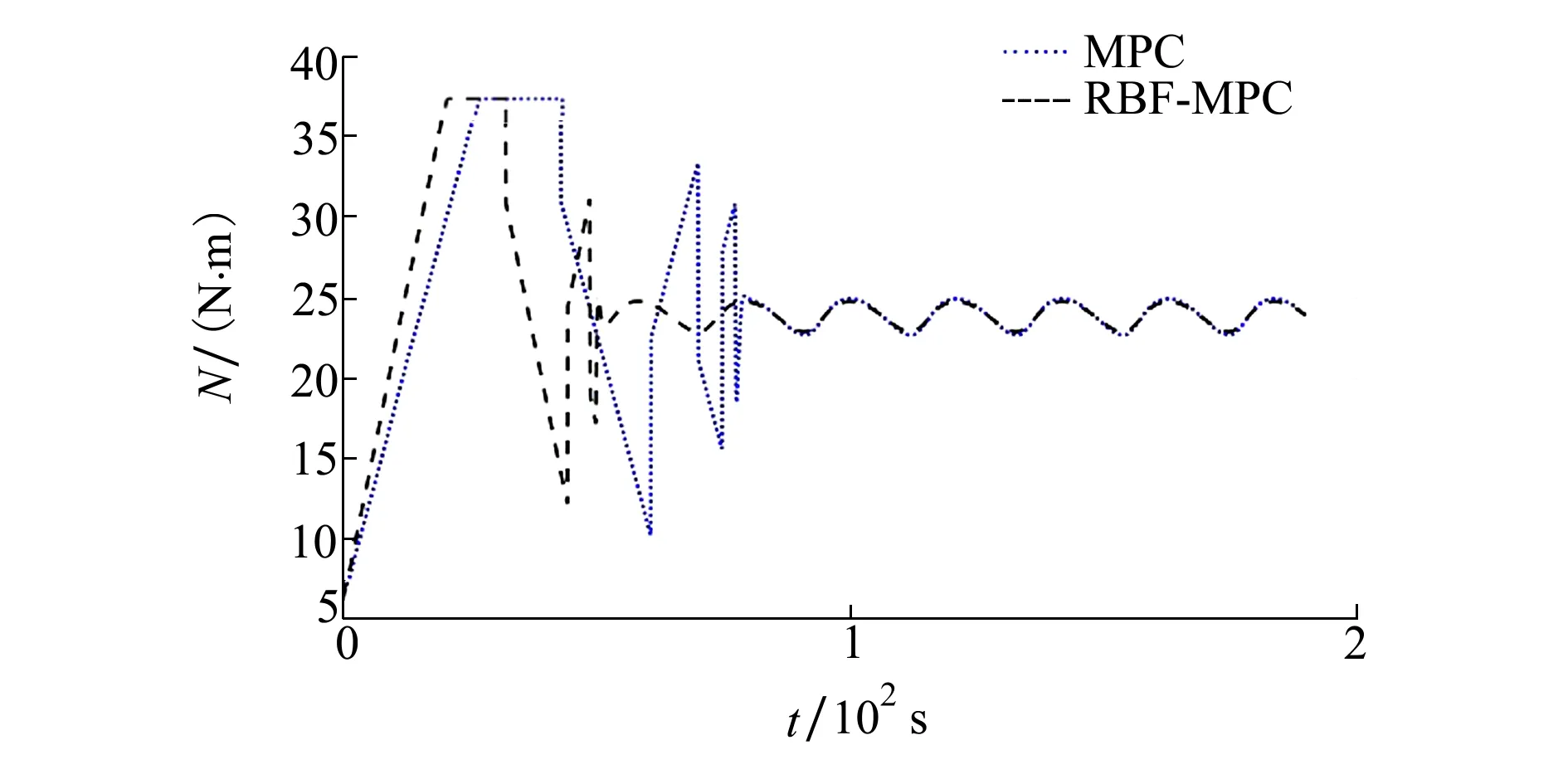
图8 控制输入力矩的变化曲线
从变化趋势上来看,RBF-MPC控制器产生的输入波动更小,特别在30,59,70 s峰值处差异较为明显,且在稳态阶段,RBF-MPC控制器得到的控制输入比较平稳。
采用2种控制器跟踪正弦波形,验证了本文提出的RBF-MPC控制器的可行性。该控制器能够有效减小模型不确定性带来的扰动,减小系统的超调和稳态误差。
3.2 参考路径仿真结果分析
设置AUV初始位置为(10 m,-10 m),依次到达目标点位置为(17 m,-56 m),(187 m,-146 m),(208 m,-234 m),(334 m,-414 m),(488 m,-488 m),(980 m,-980 m),初始航向角0,控制器的采样间隔T=0.1,预测步长N=50,仿真时间为360 s。
由图9可以看出,2种控制器都能较好地完成跟踪任务,从局部放大图可以看出,2种控制器都能产生平滑的运动轨迹,但是在转向点处,二者的差异非常明显。不论是在横坐标为30~80 m的第一次拐角路径跟踪段,还是在横坐标为350~400 m的第二次拐角处路径跟踪段, RBF-MPC控制器都比MPC控制器具有更小的超调量,能更快速地减少与期望的参考路径之间误差,具有更好的跟踪性能。
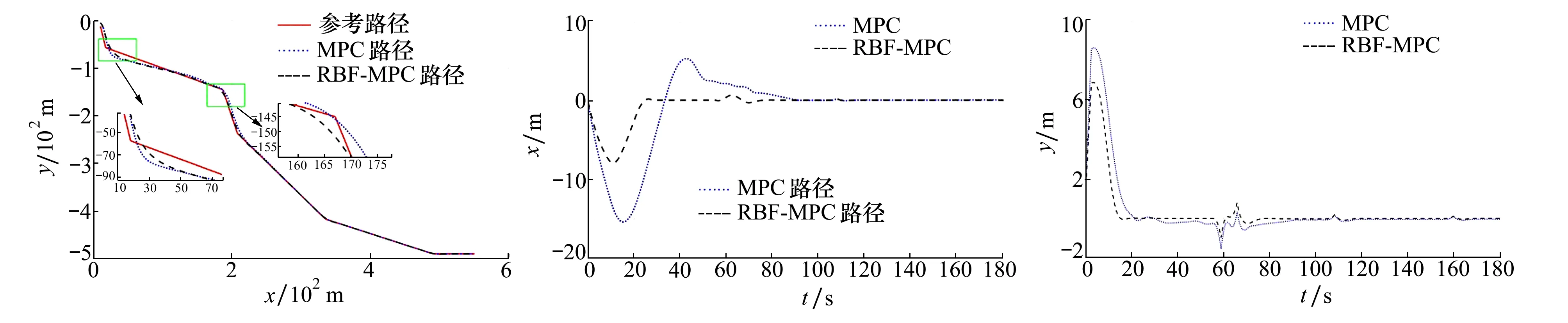
图9 路径跟踪控制结果 图10 x方向跟踪误差对比图11 y方向跟踪误差对比
为进一步清晰看出MPC控制器和RBF-MPC控制器的跟踪效果差异,将横纵向位置的跟踪偏差结果展示在图10~11。
MPC控制器在x方向的位置偏差最高可达15.5 m,而RBF-MPC控制器可以将误差减少到6.9 m,误差减少将近50%,在y方向的位置误差上RBF-MPC控制器的优势也很显著,特别是在第18 s到第75 s之间。因此,可以看出模型不确定性使MPC控制器存在较大的稳态误差,加入神经网络补偿后,超调量明显减少,更快达到稳定状态。
图12~13展示了使用MPC控制器和RBF-MPC控制器时,控制输入力和力矩的变化。从变化趋势上来看,RBF-MPC控制器产生的输入波动更小,特别在10,59,66 s峰值处差异较为明显,且在稳态阶段,RBF-MPC控制器得到的控制输入比较平稳,所耗能量更少,更利于AUV长时间水下作业。
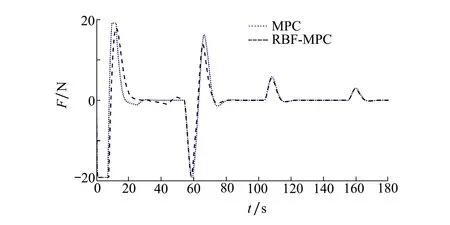
图12 控制输入力的变化曲线
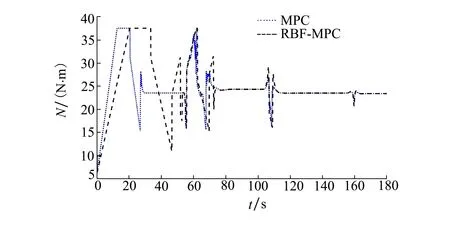
图13 控制输入力矩的变化曲线
综上所述,在存在模型不确定和扰动的情况下,RBF-MPC在控制效果方面具有更小的路径跟踪超调量和更小的稳态误差;在控制输入方面,具有更小输入幅值,更加节能。与传统的MPC控制器相比,综合优势明显。
4 结 论
本文中,针对AUV的路径跟踪控制问题,提出了基于RBF神经网络的模型预测控制器,使用RBF神经网络补偿AUV模型不确定性。仿真结果表明,在模型存在建模误差和显著不确定性的情况下,RBF-MPC控制器可以将跟踪误差减少到6.9 m,误差减少将近50%;加入神经网络补偿后,超调量明显减少,更快达到稳定状态。而且RBF-MPC控制器得到的控制输入比较平稳,所耗能量更少。综合比较, RBF-MPC控制器具有更好的跟踪性能。
