一种新型级联CDSOGI-PLL的电网电压同步信号检测技术
2023-11-21柯善文李玉忍
柯善文, 李玉忍
(西北工业大学 自动化学院, 陕西 西安 710072)
并网逆变器作为新能源与电网的接口,其控制策略的研究尤为关键,其中准确提取电网电压信息实现并网运行更是一个基本问题[1-2]。除了发生故障外,电力系统稳态运行时,电网电压也可能出现不平衡和畸变等现象[3-4]。因此,并网控制策略需要解决各种电网异常状态的问题,达到与电网的有效同步。
目前,电网电压同步信号的提取方法应用最广泛的是采用锁相环及其改进技术。当三相电网电压对称时,基于同步旋转框架SRF-PLL(synchronous rotating frame-phase locked loop)的锁相环可以准确地提取电压同步信号[5-6],但是,对于具有多种谐波的不平衡电网电压,则无法准确提取[7-8]。考虑到谐波的存在,文献[9-13]在SRF-PLL中添加了MAF(移动平均滤波器)、NF(陷波滤波器)等滤波器,用于消除双频谐波的影响,并获得电网电压同步信号。当电网频率漂移时,数字实现过程中频率估计存在误差,滤波效果受到一定影响。
由于SOGI具有频率选择和滤波功能,广泛应用于锁相环技术[14-16]。文献[17]提出基 于 双 二阶 广义 积分 器的 锁相 环 (dual second-order generalized integrator PLL,DSOGI-PLL),该锁相 环利用SOGI模块先滤除电网谐波,然后提取电网电压正序分量。该方法具有响应速度快以及暂态性能好的特点,但在电网电压含有多种谐波且低次谐波含量高时,提取的正序分量中将会出现不可忽略的纹波。考虑到在更大程度上削弱输入电压的谐波,文献[18]提出采用多个SOGI模块并联,并通过每个并联SOGI模块的输出信号交叉前馈的控制方法实现基波分量与各次谐波的分离。这种多二阶广义积分器锁相环(multiple second-order generalized integrators,MSOGI)可以准确提取电网电压的基波正序分量,但是,如果电网电压中的谐波类型未知,则无法确定SOGI模块的数量。文献[19] 在DSOGI-PLL的基础上进行了一些改进,首先消除了输入电压中的已知谐波,接着分离出输入电压的正序和负序分量并提取电网电压同步信号。结果相对准确,但是,当输入电压中存在多种谐波时,改进的锁相环需要级联多级谐波消除模块,从而增加系统延迟并降低系统的动态性能。
在 DSOGI-PLL的基础上,提出一种新型的级联SOGI锁相环结构CDSOGI-PLL。该锁相环结构利用SOGI正交输出的振幅衰减特性在PLL前端抑制输入电压中的谐波和间谐波,可以根据电网电压的失真程度灵活选择级联SOGI模块的级数,从而准确提取电网电压同步信号。
1 DSOGI-PLL
经过SOGI模块后,电网电压信号不仅可以转换为2个正交信号,而且其高次谐波也可以在一定程度上得到抑制。SOGI结构如图1所示。

图1 二阶广义积分器(SOGI)
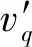
(1)
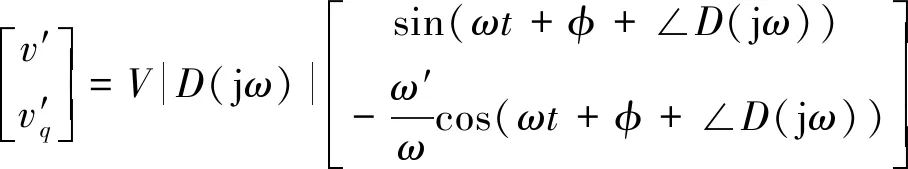
(2)
式中
(3)

(4)
对于三相电压不平衡且含有多种谐波的电力系统,传统的 SRF-PLL无法准确地检测电压同步信号,因此DSOGI-PLL在SRF-PLL基础上增加SOGI正交信号发生模块和正序分量计算模块PSC(positive sequence calculator)来分别抑制电网电压中的谐波干扰和幅值的不平衡, 其结构如图2所示。

图2 DSOGI-PLL结构图
式中,q=e-jπ/2,是一个90°滞后的移相运算。由(5)~(6)式可知,电网电压正序分量的提取需要分别获得输入信号的同相信号和正交信号。
2 新型级联CDSOGI-PLL
DSOGI-PLL中的单级SOGI模块可以衰减电网电压中出现的高次谐波。当输入信号为n次谐波时,即ω=nω0,根据(2)~(6)式可以得出同相输出端的输出信号幅值如(7)式所示
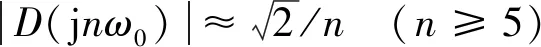
(7)
从(7)式可以看出,n次谐波经过一次SOGI模块后,同相输出端幅值经历大幅衰减, 特别地,n值越大,幅值衰减越多,n值越小时,幅值衰减越小,因此,SOGI模块具备高频滤波功能,抑制低次谐波的能力有限,对于含有低次谐波的电网条件,有必要提出一种能够衰减各种谐波的策略。
2.1 低频谐波抑制机理
通常,电网电压中的直流分量和偶次谐波分量可以忽略[19],在Clark变换后零序分量也会消除,因此,电网三相电压可表示为

(8)
对(8)式进行Clark变换,可得
式中
2.2 谐波消除模块
将(9)式输入到双SOGI模块,可得
(14)
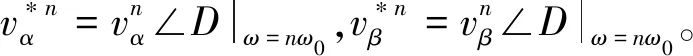
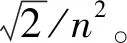
(15)
式中,n=5,7,11,13,…。这个结论同样适用于间谐波(即n大于5且不为整数)。
根据以上分析,将m级SOGI模块通过正交输出端进行级联,所得结构图如图3所示。
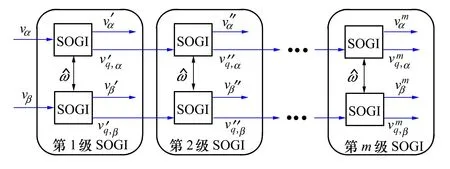
图3 m级SOGI模块级联结构
图3中,与第1级SOGI的输入谐波相比,第m级SOGI的同相输出谐波经历了大量的衰减。表1列出了图3中不同级数m的滤波系统衰减增益。

表1 图3中不同m值的谐波衰减增益 dB
为分析方便,以下按照SOGI模块级数m来标记不同的方法,其中m=1表示方法一,即传统DSOGI-PLL;m=2和m=3分别表示本文所提方法CDSOGI-PLL的2级和3级结构;m=4表示文献[19]提出的改进型DSOGI-PLL方法。
很明显,从表1中可以看出,SOGI模块级数m每增加1时,所有次谐波的衰减增益成比例增加。当采用方法一时,各次谐波的衰减增益较小,尤其是n=5,7,低次谐波,只有在电网电压发生轻微畸变时才能勉强适用。当电网电压低次谐波含量较大时,适合采用方法二,并且依据电网电压畸变程度大小来选择不同的级联结构,如可选择m=2或m=3。当m=3时,电网中存在的所有次谐波均可以被大量削弱直到可以忽略不计。虽然在m=4时,即方法三,各次谐波可获得理论上无穷大的衰减增益,但前提是谐波成分必须已知,另外,m取值越大系统快速性能越弱。因此,锁相环方法的选择需要综合考虑系统的动态性能和抗干扰性能2个因素。
2.3 改进型的锁相环结构
根据以上分析结论可知,不考虑谐波相位,对于谐波次数n≥5,谐波含量经过m级SOGI模块滤波后可以忽略不计,因此,最后一级2个SOGI模块的同相输出和正交输出可以近似重写成为(以m=2为例):
(16)~(17)式都仅含有基波的α,β轴正负序分量,通过简单的数学操作可以将基波的正序分量提取出来。
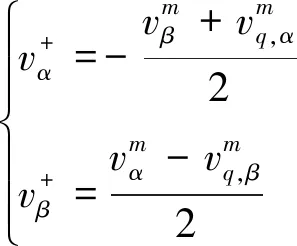
(18)
改进后的锁相环结构如图4所示。
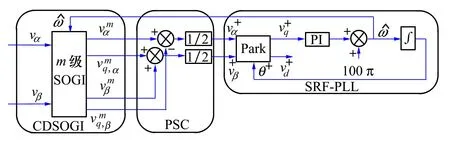
图4 CDSOGI-PLL结构
图4中第一部分是指m级SOGI模块级联的滤波结构CDSOGI,其可以采用上面提到的2种滤波结构,第二部分是PSC, 第三部分为传统SRF锁相环结构。
3 系统特性分析
3.1 系统稳态特性
图5为2级SOGI模块级联结构,该结构的空间状态方程可以写成(19)式,式中x是状态变量,y是输出变量。很明显,SOGI模块表现为一个非线性系统,系统中的动态响应和稳定性取决于3个参数,也就是输入信号的幅值、频率和K的值。
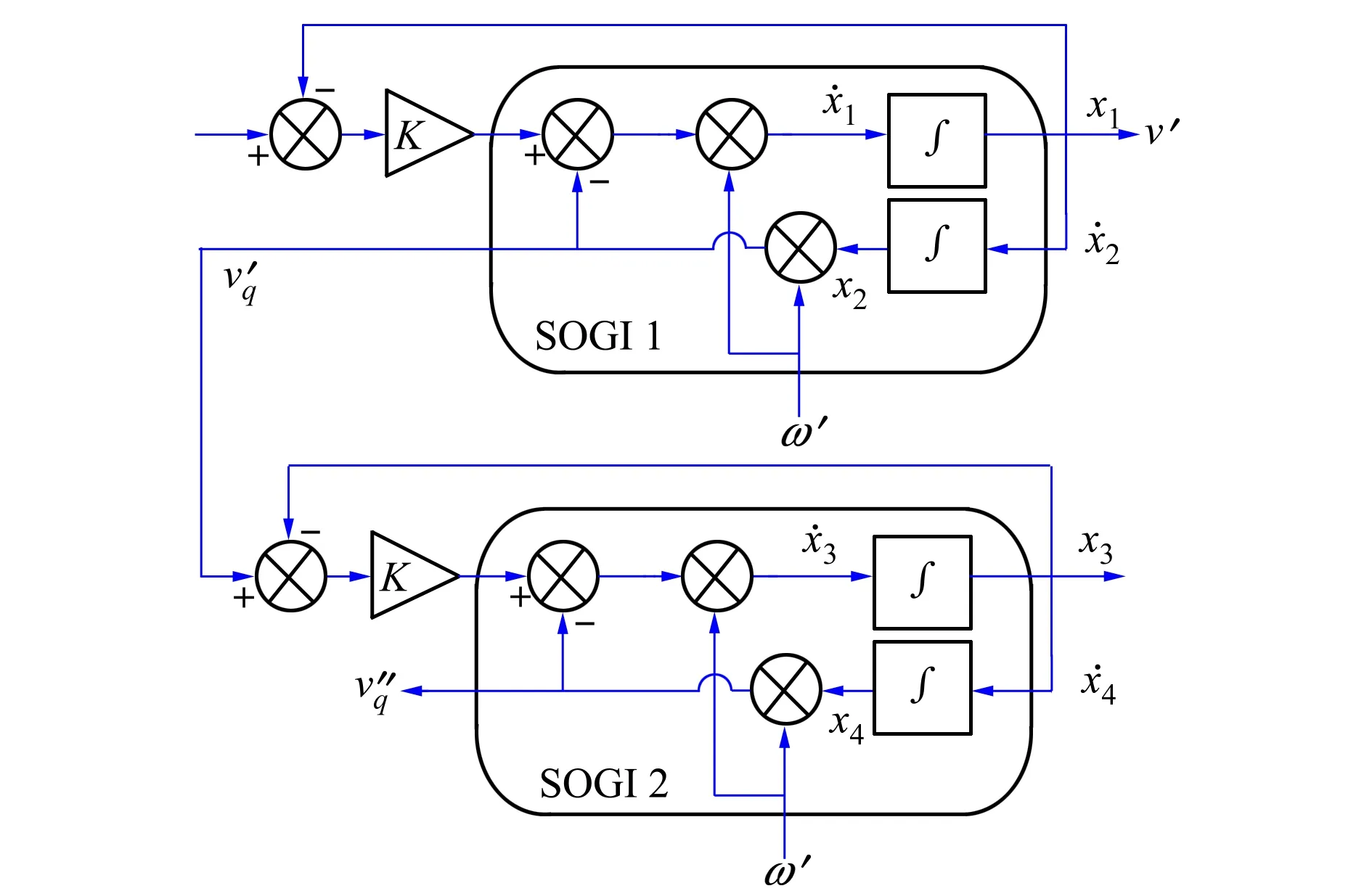
图5 2级SOGI 模块级联结构图
考虑到稳态运行条件,当x1=v和x3=qv′=x2ω′,(19)式可以变换为
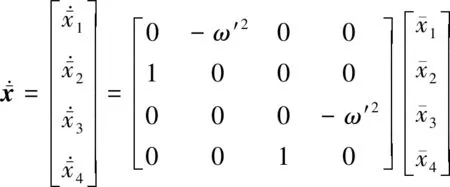
(21)

3.2 系统动态特性
参考SOGI传递函数,考虑到频率ω′≈ω且为一个常数,对于给定的正弦输入信号v=Vsin(ωt+φ),单个SOGI模块的同相端输出时域响应可以写成
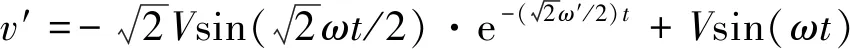
(22)
然而,2级SOGI模块级联时,对于同样的正弦输入信号,第二级SOGI模块同相端输出时域响应表达式为
(23)
从(22)~(23)式可以看出,等式右边由两部分组成,暂态分量和稳态分量,系统到达稳定时,稳态分量与初始输入信号相比除了相位发生偏移外,幅值和频率不变。然而,两式中的暂态分量均为指数衰减函数,不同的是指数函数的系数不同,为考察不同个数SOGI模块级联时到达稳态时的调整时间,现对2个衰减函数进行对比分析(令V=1.0 V),如图6所示。
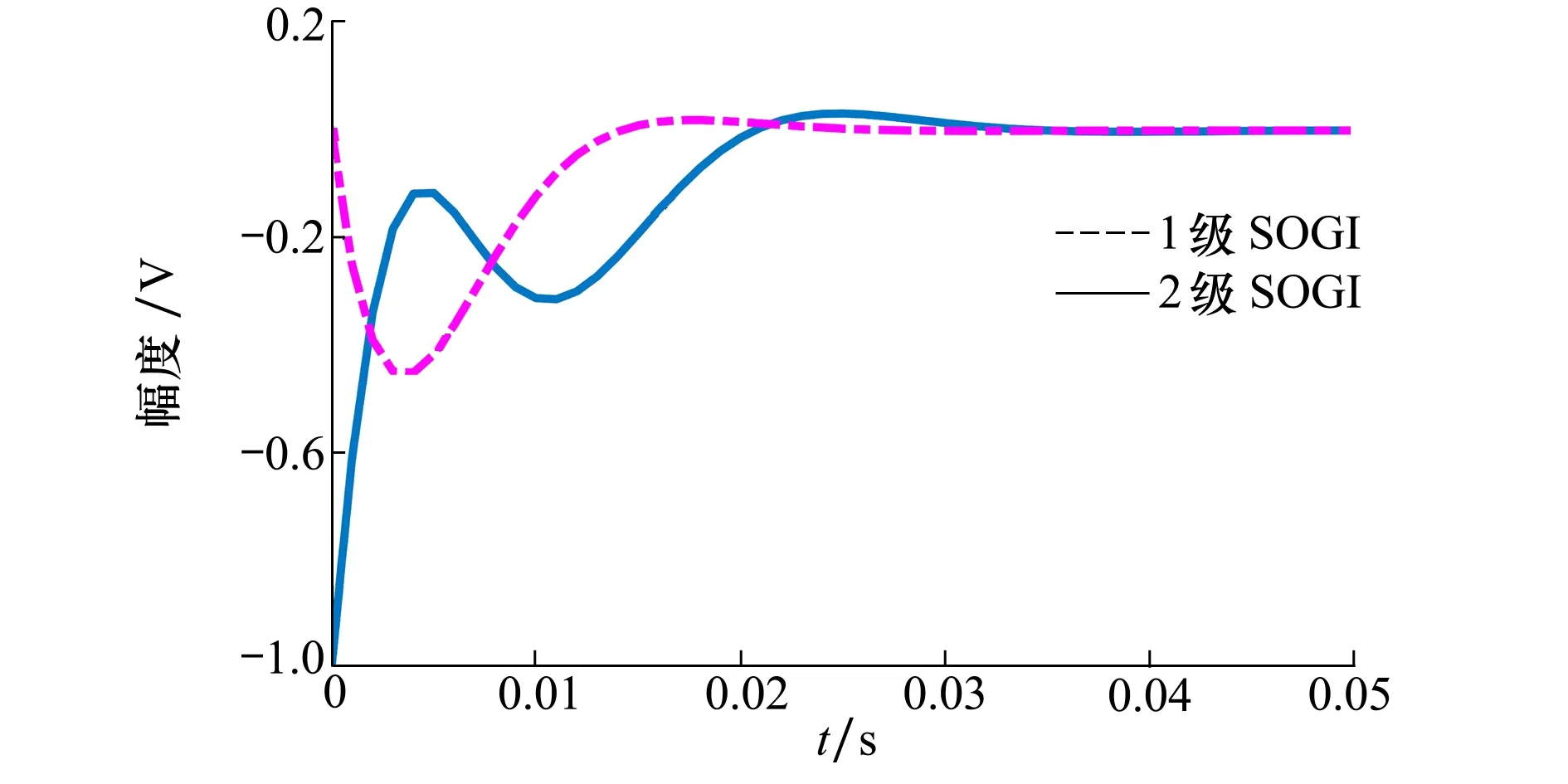
图6 (22)和(23)式暂态分量的波形
从图6中可以看出2级SOGI模块级联时,信号中的暂态分量衰减至零的时间很显然比单SOGI模块时更慢,由于SOGI模块的滤波器特性,从而可以得出每增加一个SOGI 模块稳态输出调整时间均有所增加。模块数的增加会影响系统的动态性能,因此有必要在谐波抑制效果和系统的动态性能之间取得平衡。
4 仿真及实验
4.1 仿真分析
为了进一步验证提出的CDSOGI-PLL的可行性和有效性,采用Matlab/Simulink搭建系统的仿真模型的方式,将其与传统的DSOGI-PLL和文献[19]提出的改进型DSOGI-PLL进行比较分析。3种锁相环系统分别在相位跳跃、频率突变、电压幅值降落等工况下进行仿真比较。几种工况设置具体如下:
工况1t=0.25 s时,电网频率突然增加3 Hz,t=0.5 s时,电网电压加入20%的5次谐波,10%的7次谐波以及5%的11次谐波。
工况2t=0.25 s时,电网电压相位突变20°, 电网电压加入20%的5次谐波,10%的7次谐波以及5%的11次谐波。
工况3t=0.25 s时,电网电压降落0.3 pu,t=0.5 s时,电网电压加入20%的5次谐波,10%的7次谐波以及5%的11次谐波。
实验条件表明,谐波种类共有3种且5次谐波含量较高,因此采用文献[19]中方法时需要级联4级SOGI模块(m=4)。为比较各种锁相环的动态性能,仿真和实验除了采用传统DSOGI-PLL和文献[19]中的方法外,基于CDSOGI的结构一(m=2)和结构二(m=3)也包含在内。3种工况下3种锁相环的仿真结果如图7所示。当0.25 s时输入电压频率、相位、电压幅值分别发生突变,对3种方法在暂态过程中的调整时间进行比较,很显然,方法一(m=1)最短,方法三(m=4)最长,方法二中的结构一(m=2)较结构二(m=3)更短。0.5 s时电网电压加入谐波,从图中可以看出,方法一(m=1)抑制谐波能力最差,稳态频率和相位差受谐波影响较大;而另外2种方法都能够很好地消除谐波的影响且抑制效果接近。因此,采用CDSOGI-PLL,级联更少的SOGI模块可以同时获得较满意的滤波效果和较好的动态性能。

图7 各种锁相环的频率估计和相位误差仿真波形
4.2 实验验证
为了进一步验证文中所提方法的有效性和硬件可实现性,本次实验采用了1套电网电压同步信号检测实验装置,主控芯片采用TI公司的TMS320F28335数字信号处理器,不仅实现算法的数字运算,同时可以模拟产生实验所需的各种工况下的电网电压信号。DSP主芯片的采样频率设置为10 kHz,在中断程序中模拟实际电网的几种工况,实验中生成的波形数据通过缓存和串口通信传输至上位机软件,并绘制出图形。实验设定的3种工况与仿真一致,各种参数波形见图8。
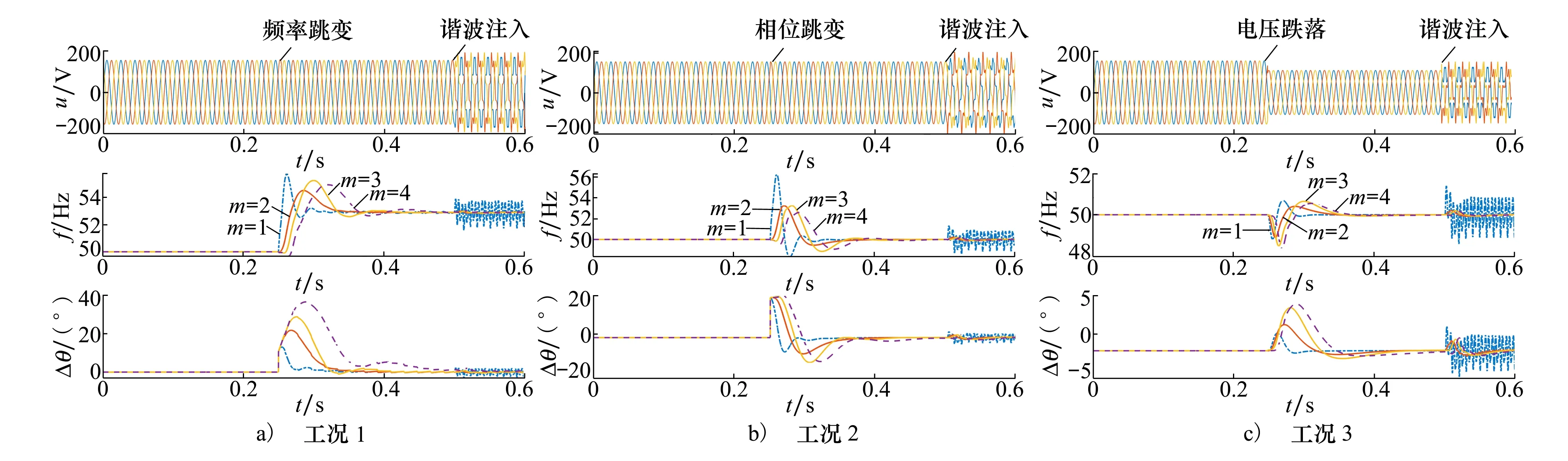
图8 各种锁相环的频率估计和相位误差实验波形
很明显,图8中实验波形与相应的仿真波形基本保持一致。频率、相位差在到达稳态后波形均表现出轻微振荡,跟3.1节稳态分析结论相吻合,另外,随着SOGI模块级数m的增加,系统动态性能随之变慢,验证了3.2节动态过程分析结论的正确性。从图8a)~8c)可看出,0.25 s时电网电压发生频率突变、相位跳跃以及电压幅值骤降,相比方法二(m=2,3),方法三(m=4)需要更长的调整时间。0.5 s时谐波加入后,方法一(m=1)由于不能完全抑制谐波,频率和相位跟踪动态波形出现较大振荡,方法二中结构一即2级SOGI模块级联,在谐波严重时不具备足够的抑制能力,故图中波形(m=2)有轻微振荡;而方法二中结构二即3级SOGI模块级联和方法三提供了充分的谐波衰减增益,因此,图中波形(m=3)和波形(m=4)呈现出一条近似平坦的直线。
表2中列出了m取不同值时,锁相环系统的耗时成本比较。从表中数据可知,随着m值的增大,系统耗时成比例增加,因此,在满足谐波抑制要求的前提下,m的取值不宜过大,以防加重系统计算负担。

表2 不同m值的系统计算时间成本
5 结 论
传统的DSOGI-PLL在电网电压含有大量低次谐波时无法正常工作,文献[19]中的方法在已知谐波成分的前提下获得很好的谐波抑制效果,但由于级联的SOGI模块过多而导致动态性能差。CDSOGI-PLL采用新的SOGI模块级联方式,可以在电网电压谐波成分已知或未知的情况下用最少的SOGI模块很好地抑制谐波,并保持较好动态性能。另外,实际应用时可根据电网电压畸变程度选择SOGI模块的级联级数m=2或m=3,从而在复杂的电网条件下能同时获得较好的综合性能。
