永磁同步电机无参数三矢量模型预测电流控制

张玉峰, 吴紫辉, 闫琪, 黄楠, 杜光辉, 贺虎成, 周勇

(1.西安科技大学 电气与控制工程学院, 陕西 西安 710054; 2.西北工业大学 航空学院, 陕西 西安 710072)

永磁同步电机(permanent magnet synchronous motor,PMSM)具有体积小、效率高等优点,在电动汽车、航空航天等领域获得了广泛青睐[1]。传统矢量控制和直接转矩控制存在带宽窄、转矩脉动较大等不足,限制了PMSM在高控制精度和高鲁棒性场合的应用[2]。

模型预测控制(model predictive control,MPC)可处理非线性多目标参数、动态响应迅速,适合多变量、强耦合的PMSM系统,近年来成为PMSM控制领域的研究热点[3-4]。经典MPC在控制周期内应用单个电压矢量并不断滚动优化来使电机具有良好的动态性能,但电机的稳态性能却不尽如人意。为此,有关学者提出在控制周期内应用多个电压矢量以提升稳态性能。文献[5-6]引入占空比模型预测控制,即通过单个周期内施加1个最优有效电压矢量和1个零矢量调节输出电压矢量的幅值,减小电机电流脉动,但输出的电压矢量角度仍然固定。文献[7-8]将占空比模型预测控制中的零矢量换成有效电压矢量,形成双矢量模型预测控制,使得逆变器输出电压矢量角度、幅值均可调,但由于未加入零矢量调节,电压矢量幅值范围仍然有限。为此,有关学者提出2个有效电压矢量和1个零矢量组合的三矢量MPC策略[9-10]。三矢量MPC策略下的逆变器输出电压更接近理想电压矢量,电机的稳态性得到较大改善,但存在矢量组合选择复杂、计算量大等不足。

模型预测控制依赖电机本体模型去构建各类控制目标的预测模型,易受本体参数的影响。为提升控制的鲁棒性,文献[11]以预测误差为评价目标,推导了定子电流预测误差与参数摄动之间的数学模型,并分析和验证了电机电感参数的变化对性能影响较大。为摆脱电机参数的束缚,学者们将无模型思想引入到PMSM的预测控制中,如基于增量模型的预测电流控制可以在不引入电机参数的情况下对系统下一时刻状态进行估算,但需要在一个控制周期内采集2次定子电流,对系统硬件要求高[12-14]。

Fliess提出了一种基于系统输入输出构建超局部模型的无模型控制方法,该方法无需被控对象的具体参数,提高了控制策略的鲁棒性[15-16]。该方法在文献[17]中被成功应用于表贴式PMSM中,证明了可行性与有效性。文献[18]在经典超局部模型预测控制的基础上加入了前馈非线性扰动补偿,在减少调参工作量的基础上改善了系统的动态性能和交直轴电流谐波。传统三矢量预测控制算法中,预测模型和矢量作用时间计算都涉及电机参数,对电机参数变化更加敏感。文献[10]对各环节进行误差分析并予以误差补偿,一定程度上改善了三矢量模型预测电流控制在电机参数失配情况下的稳态控制性能。文献[19]利用参数辨识法对超局部模型中的未知部分进行了估算,摆脱了电机参数的束缚,但需要采集并存储数个控制周期内的电流、电压,且未对电机参数变化影响进行分析。

为提高三矢量模型预测电流控制的鲁棒性,同时兼顾控制性能,本文提出一种无参数三矢量模型预测电流控制(nonparametric three-vector model predictive current control,NTV-MPCC)。所提方法基于无模型控制思想,仅依据电机输入输出信号构建超局部电流预测模型,抑制电机本体参数摄动对传统三矢量模型预测电流控制(three-vector model predictive current control,TV-MPCC)中预测模块的影响。针对传统有参数多矢量控制策略中电压矢量作用时间计算易受电机本体参数影响的问题,引入基于电流误差的矢量作用占空比直接计算法。此外,通过设计电压代价函数和重新划分矢量扇区,优化了三矢量组合的选择过程,减少了算法实施复杂度。最后通过仿真和实验验证了所提方法的有效性。

1 基于超局部模型的PMSM无参数预测电流原理

1.1 考虑扰动因素的PMSM数学模型构建

为建立更符合电机实际运行的数学模型,可将参数扰动项、外部扰动项以及系统未建模项引入到PMSM的理想数学模型中,得到考虑扰动因素的PMSM数学模型为

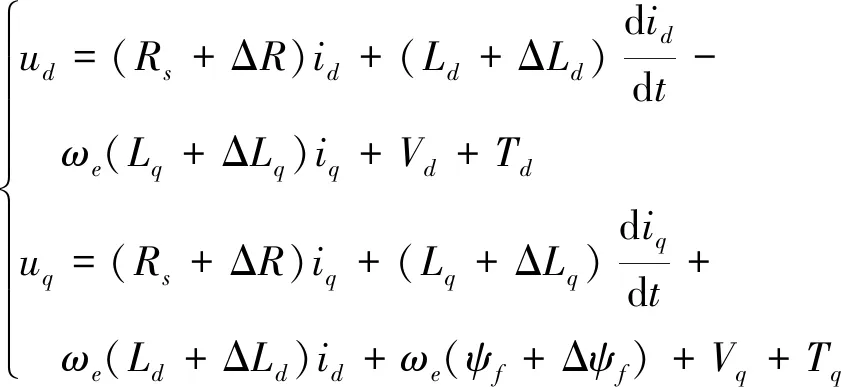
(1)

式中:ud,uq代表定子d,q轴电压;id,iq代表定子d,q轴电流;Ld,Lq代表d,q轴电感;Rs为定子电阻;ωe为电角速度;ψf为永磁体磁链;ΔR,ΔLd,Lq,Δψf为电机参数摄动量;Vd,Vq代表d,q轴的未建模部分;Td,Tq分别为d,q轴外部扰动项。

可将电机在d,q轴上的未建模和集总扰动部分分别表示为fd,fd

(2)

则(1)式可简化为

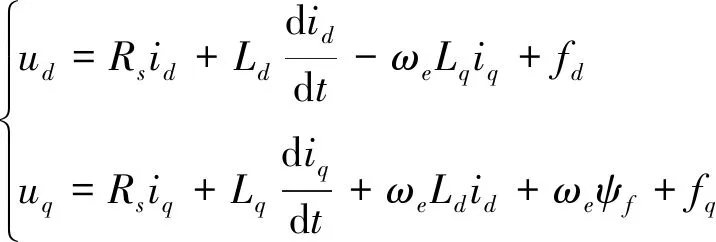
(3)

(3)式即为考虑系统扰动因素后的PMSM数学模型。

1.2 PMSM超局部预测电流模型设计

由PMSM数学模型可得PMSM超局部模型为

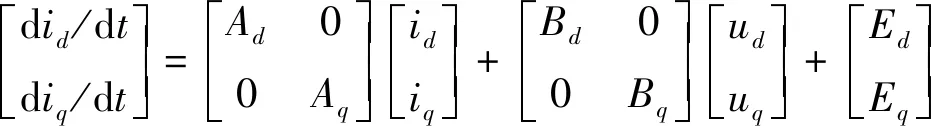
(4)

式中:Ad,Aq分别代表d,q轴的电流系数;Bd,Bq分别代表d,q轴的电压系数;Ed,Eq分别代表d,q轴未建模与集总扰动部分,电流和电压系数通常为常数并由设计者调校。

将(4)式进行离散化可得到PMSM超局部电流预测模型

(5)

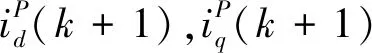
1.3 全阶离散扰动观测器设计

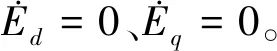
(6)

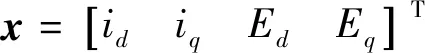
基于(6)式构建全阶扰动观测器为

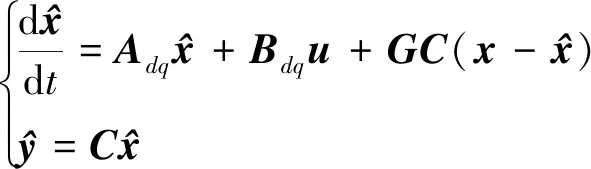
(7)

将(7)式构建的扰动观测器进行离散化可得

(8)

式中

由现代控制理论可知,观测器的稳定性主要由系统特征矩阵的特征值决定,若所有特征值位于Z域的单位圆内,则观测器能够最终趋于稳定。可通过设计反馈增益系数使观测器达到稳定状态。

观测器特征方程如(9)式所示

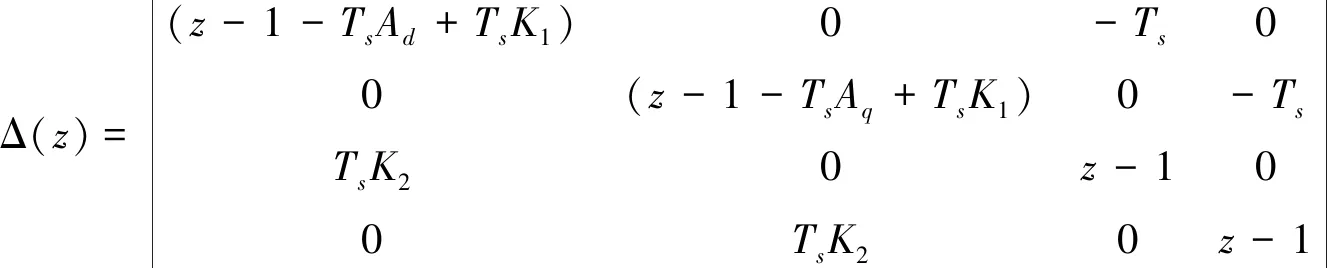
(9)

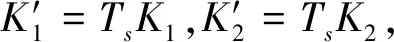
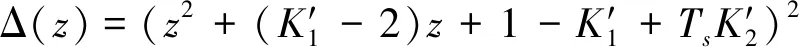
(10)

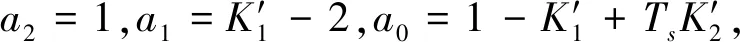
Δ(z)=(a2z2+a1z+a0)2

(11)

依据朱里准则对观测器进行稳定性分析,结合(11)式可得到3条系统稳定性判据

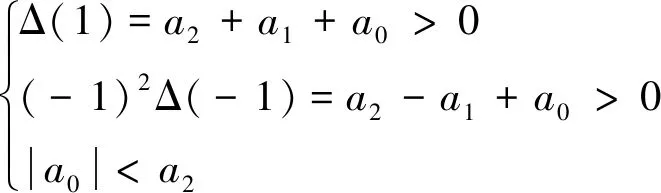
(12)

将a2,a1,a0对应代入(12)式可得

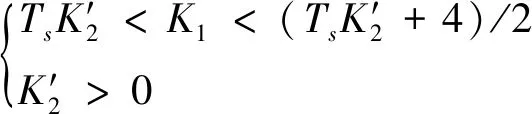
(13)

当K1,K2取值符合(13)式时,扰动观测器即可收敛。

2 PMSM无参数三矢量预测电流控制

2.1 三矢量选择原则

本文采用三相两电平电压型逆变器驱动PMSM,其输出的空间电压矢量如图1所示。

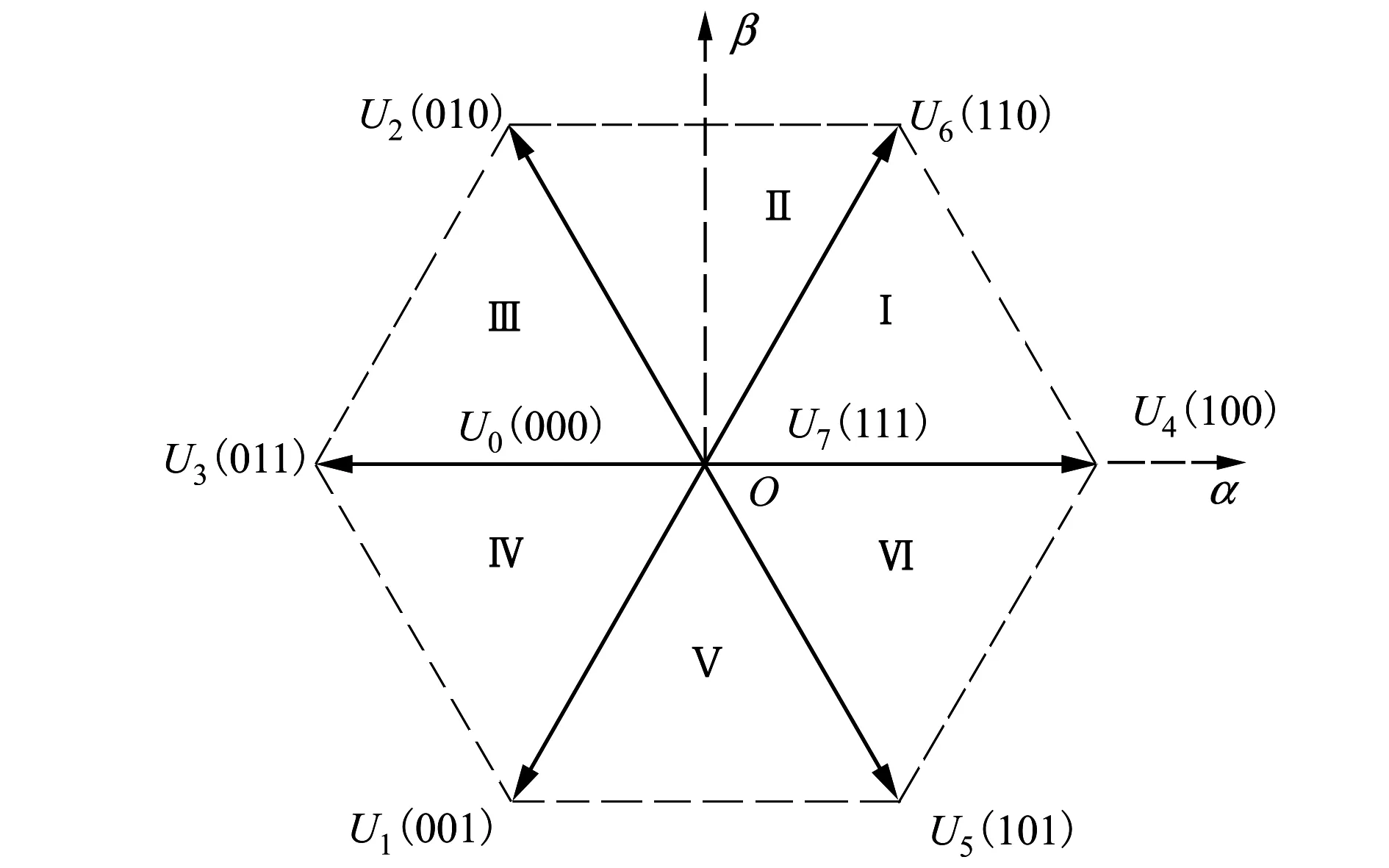
图1 逆变器基本电压矢量示意图

传统TV-MPCC采用2轮遍历法获取最优矢量组合,对硬件资源要求较高。为减小算法复杂度,本文将原有的电流代价函数改为电压代价函数,在第一轮遍历中省去电流预测值的计算;同时利用第一最优矢量与理想电压矢量的差值进行第二最优矢量选择,避免了第二轮遍历,具体实现思路如下。

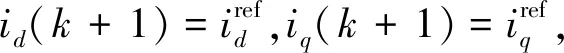
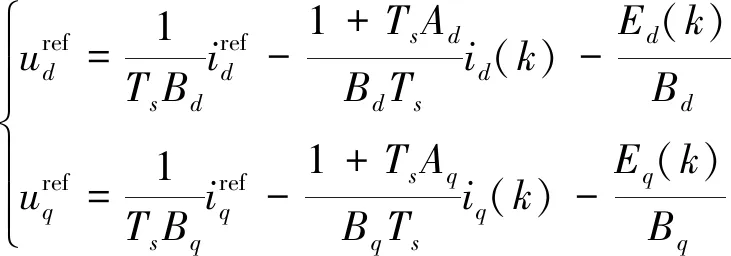
(14)

由反Park变换获得两相静止坐标系下的参考电压

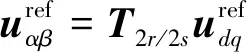
(15)

将传统电流矢量代价函数改写为电压代价函数

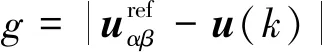
(16)

代入6个有效电压矢量遍历寻优,即可获得第一最优电压矢量uopt1。

进而计算uopt1与理想电压矢量的差值

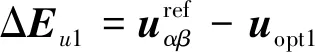
(17)

将原有电压矢量分布图重新划分为6个区域,如图2所示。判断误差电压矢量ΔEu1所处区域,选择扇区中心矢量为第二最优矢量uopt2。例如ΔEu1位于扇区S2,则第二最优矢量为U6(110)。第三矢量选择为零矢量,记为uopt0。

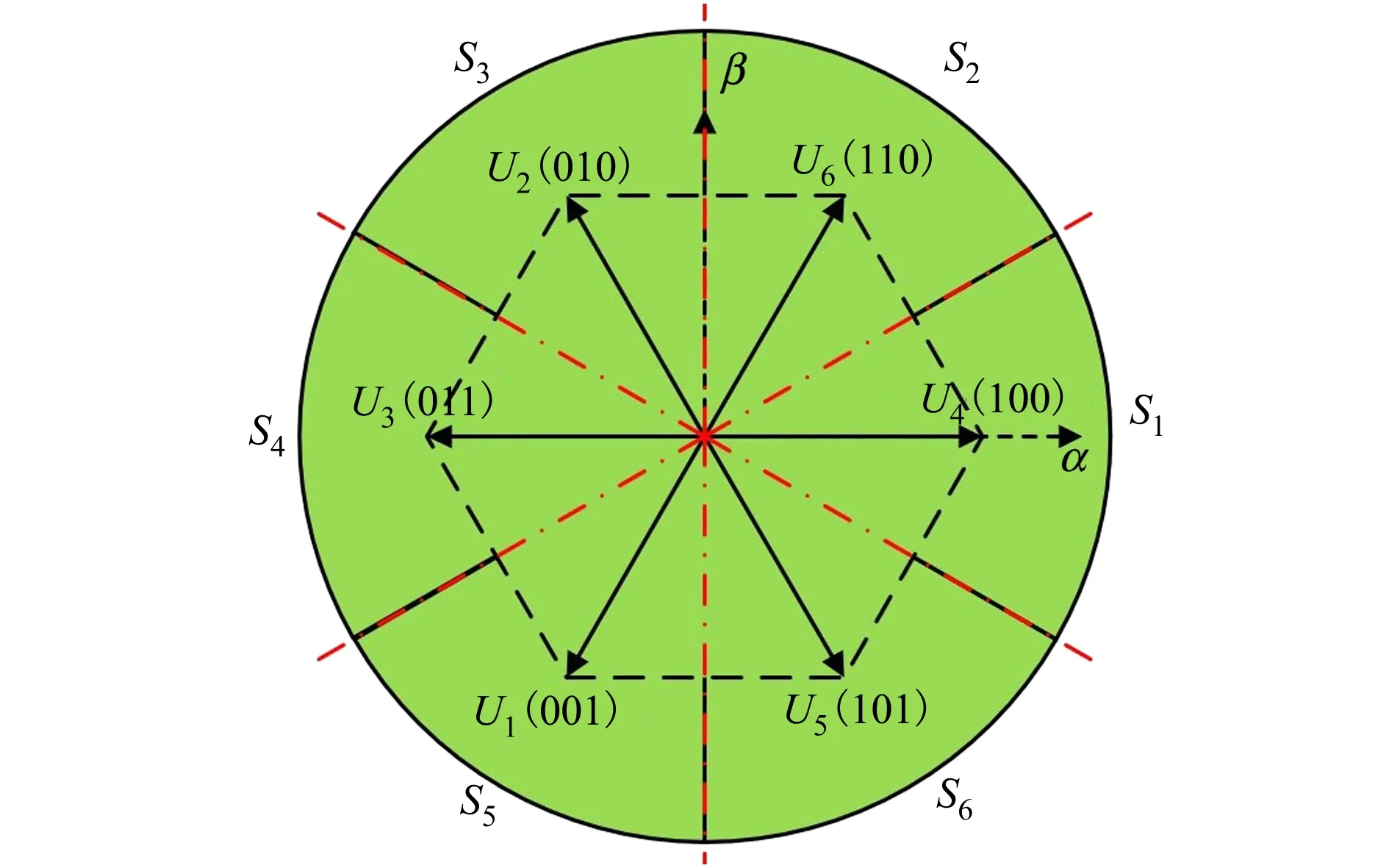
图2 新扇区划分示意图

2.2 基于电流误差的矢量作用时间计算

传统三矢量策略多基于电流斜率计算各个电压矢量作用时间,计算过程涉及多个电机参数。当电机参数失配时易导致矢量作用时间计算失准,降低了控制的准确性和稳定性。本文借鉴文献[11]中转矩控制算法中矢量占空比的计算思路,设计了基于电流误差的矢量作用占空比直接计算法,并优化了占空比计算输出值,以抑制占空比的过调制。具体思路为:

规定uopt1的占空比为d1,uopt2的占空比为d2,uopt0的占空比为d0。计算3个电压矢量电流预测值与电流参考值的差值为

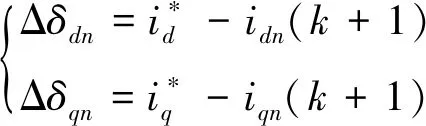
(18)

式中:Δδdn,Δδqn分别代表d,q轴预测电流与参考电流的差值;n为1,2或0。

则由电流无差拍原理可得占空比计算式为

(19)

由(19)式计算所得的三矢量占空比可能存在过调制的情况,故对三矢量占空比进行优化

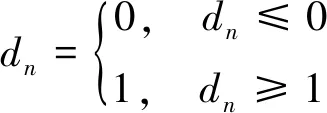
(20)

n为1,2或0。

经(20)式优化后判断d1+d2≥1是否成立,若成立,则执行(21)式,否则直接输出相应矢量占空比。

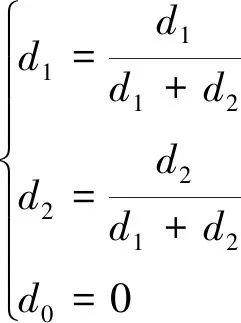
(21)

2.3 NTV-MPCC控制策略

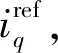
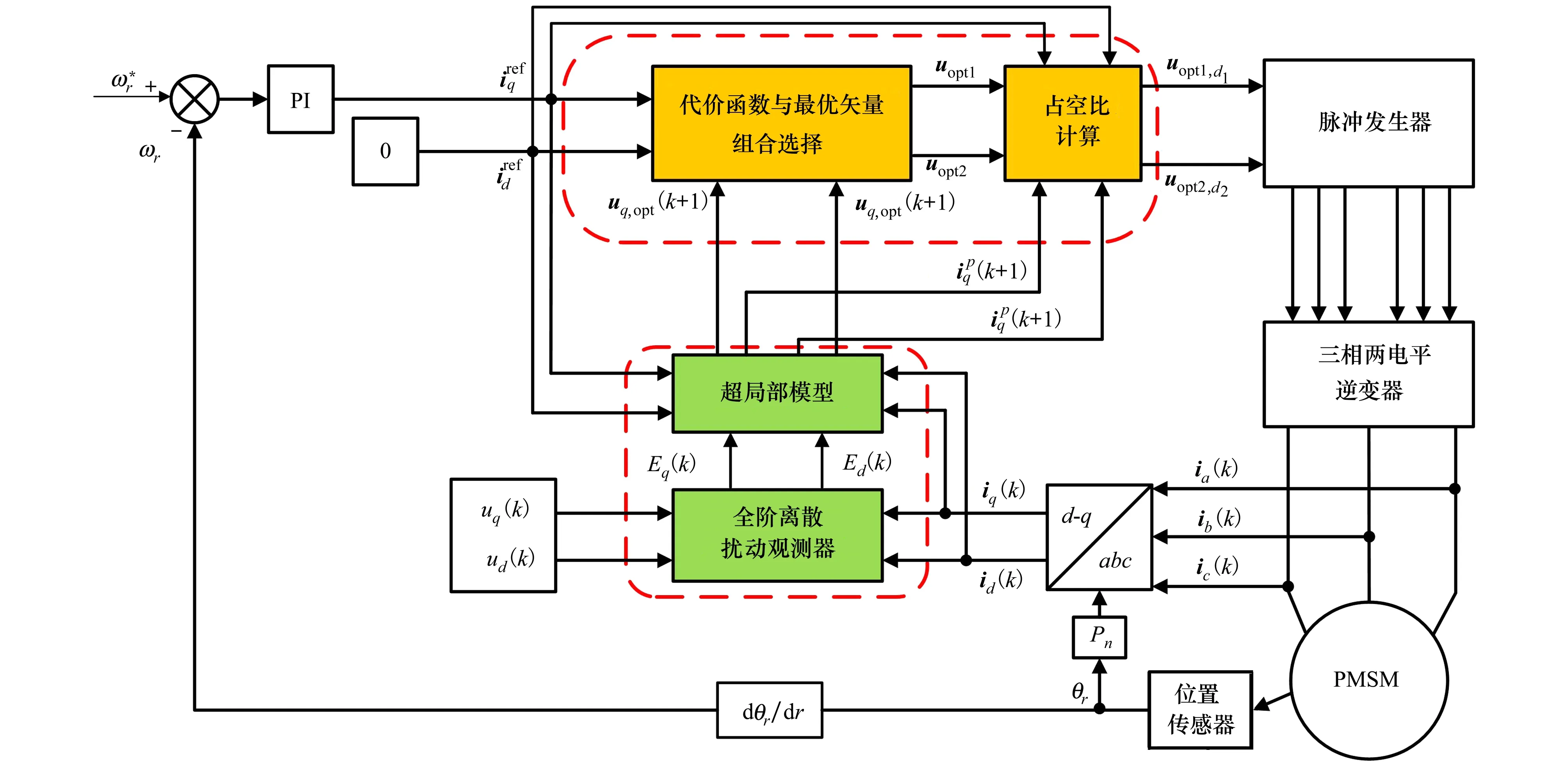
图3 无参数三矢量模型预测电流控制系统框图

3 仿真分析

利用MATLAB/Simulink对算法进行仿真验证,电机参数如表1所示。控制周期设置为100 μs,分别对起动、加速、加载和电机参数失配工况下的控制性能进行验证。

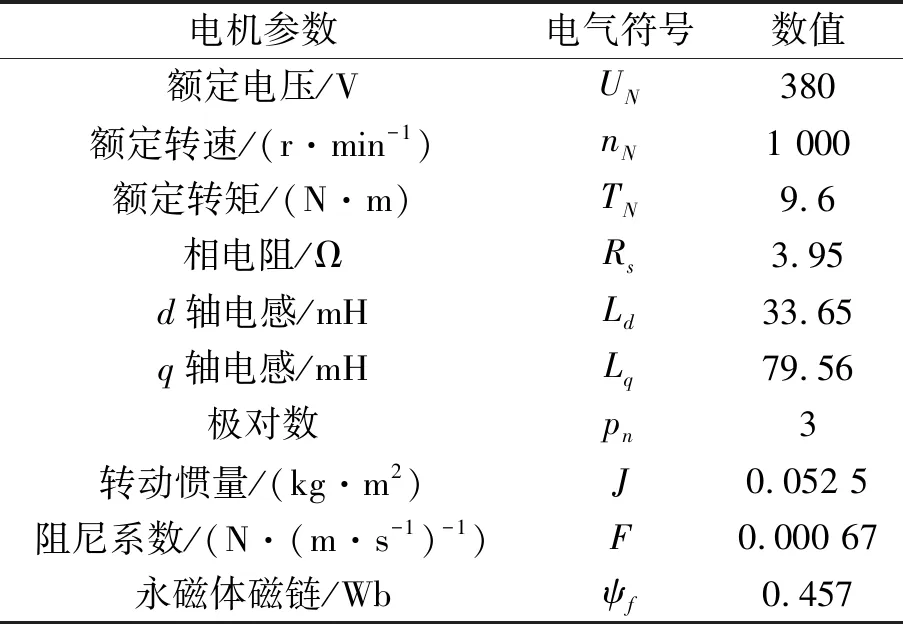
表1 PMSM参数标称值

起动、加速及加载工况仿真波形如图4所示,电机初始参考转速给定500 r/min,0.3 s时转速指令增至1 000 r/min,0.7 s时电机加载9.6 N·m。

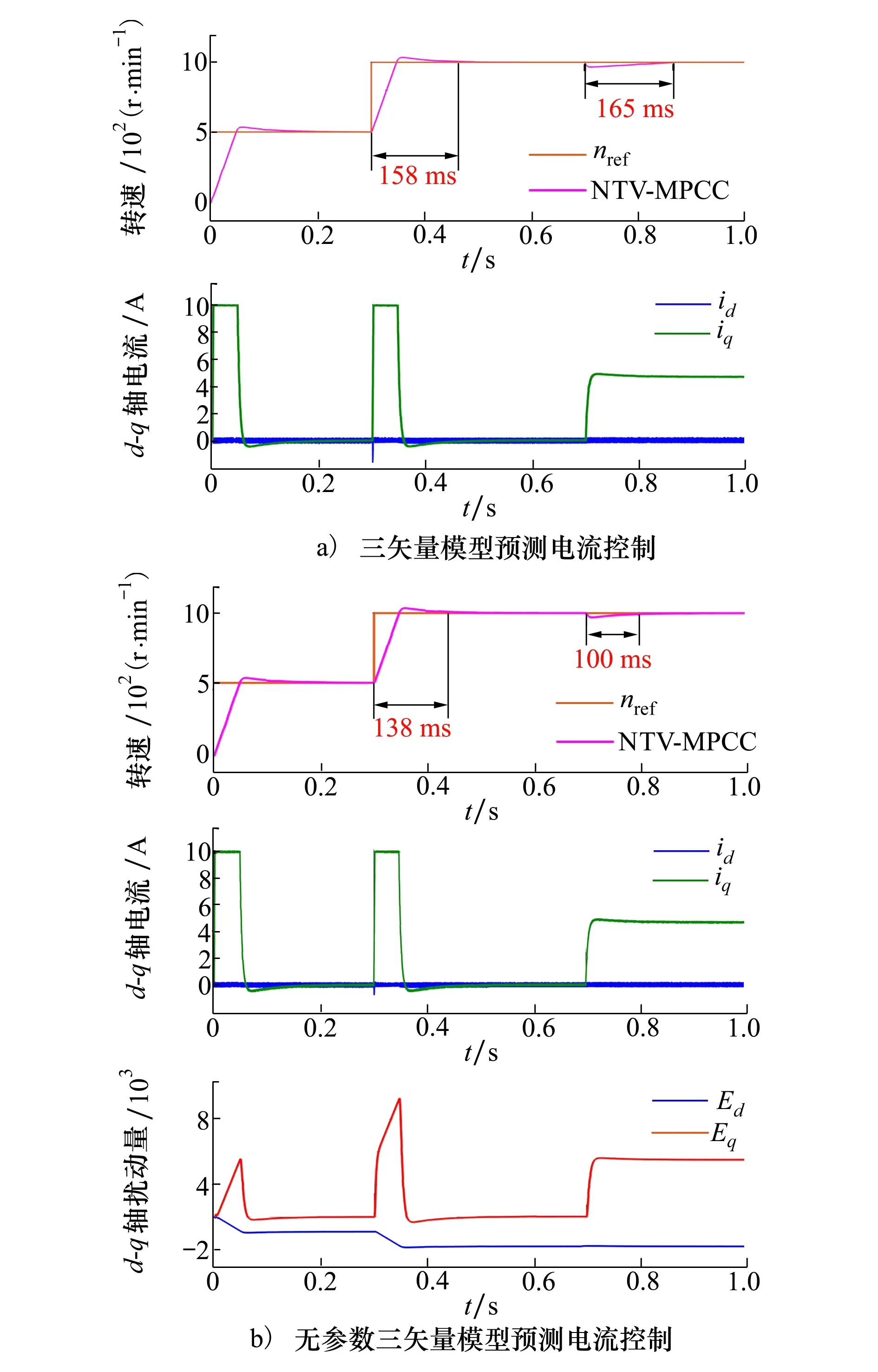
图4 电机起动、加速及加载工况仿真对比图

由图4a)～4b)转速和电流波形可看出,在电机参数未摄动时,传统TV-MPCC策略与NTV-MPCC策略的稳态性能相似,但NTV-MPCC动态性能优于TV-MPCC。电机从500 r/min升至1 000 r/min,TV-MPCC耗时158 ms,而NTV-MPCC仅用时138 ms。TV-MPCC控制下,电机加载后165 ms稳定在给定转速,而NTV-MPCC仅用时100 ms,证明所提NTV-MPCC策略能在确保稳态性能的基础上提升电机的抗扰性和调速过程。

由图4b)中系统d-q轴集总扰动观测量可以看出,d-q轴扰动观测值能随着系统状态的改变而迅速变化。在0.3 s时电机转速由500 r/min上升至1 000 r/min,此时q轴扰动观测值也随之变化。在0.7 s电机加载时,d轴未知扰动量观测值也随之迅速变化,且观测值与未建模以及扰动变化比例相吻合,证明本文所设计的观测器能够准确估计系统未知量,并使电机控制系统维持稳定。

电机参数失配工况的仿真波形如图5所示。电机转速设定为500 r/min,带载5 N·m。在0.2 s时d-q轴电感分别下降为0.5Ld,0.5Lq,0.6 s时恢复为1.0Ld,1.0Lq,1.0 s时上升为2.0Ld,2.0Lq。

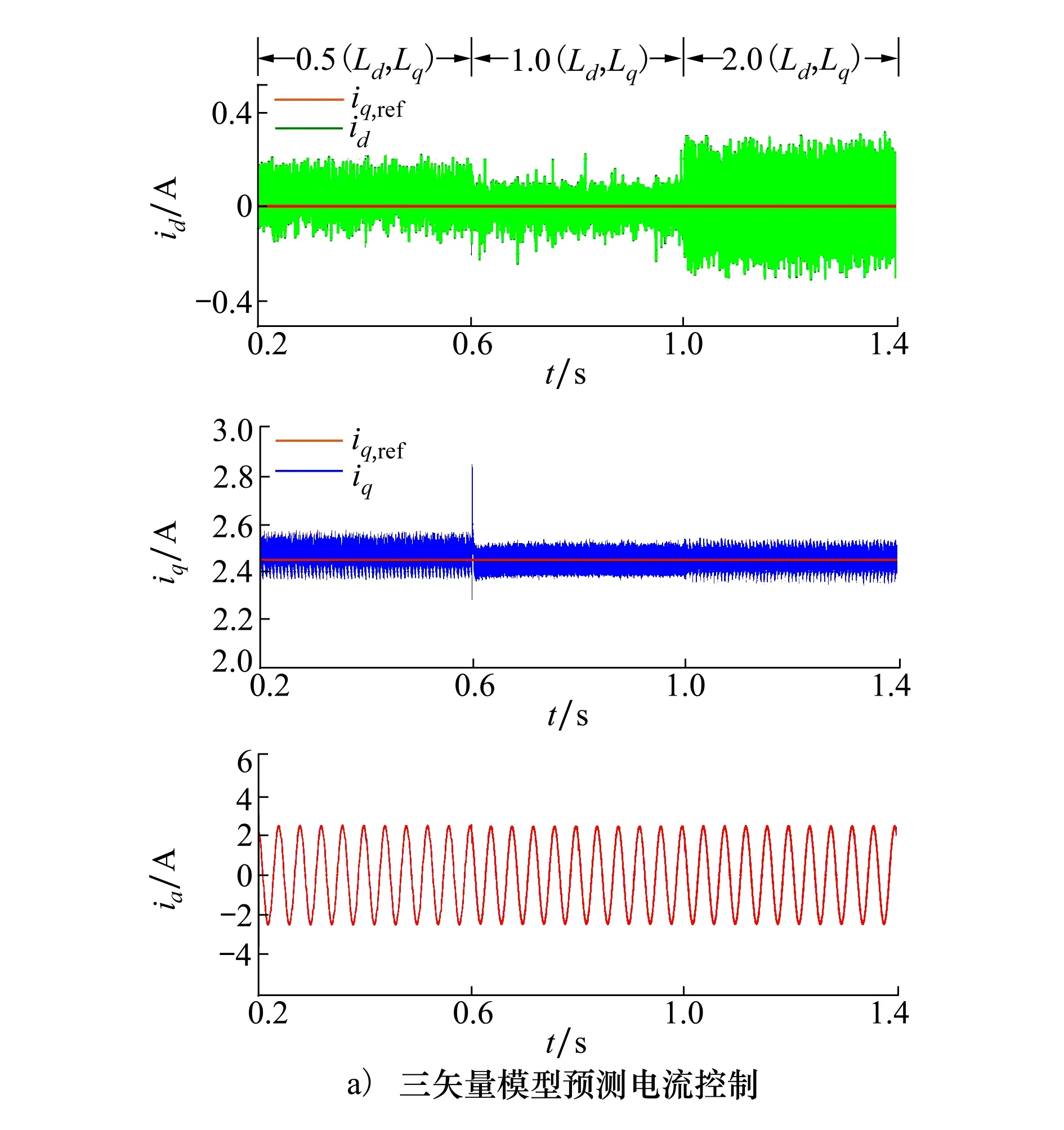
图5 电感参数失配情况下电机稳态性能仿真对比图

从图5a)可以看出,传统TV-MPCC对于电感参数变化十分敏感,d-q轴电流都出现了偏移给定值和纹波增大的现象,说明参数变化对传统TV-MPCC策略有较大的影响。而在图5b)中,电机电感参数变化前后电机状态变化微弱,d-q电流脉动较小,且能很好地跟随给定值,表明所提策略具有强鲁棒性。由图5b)中系统扰动观测图可以看出系统扰动观测值随电感参数改变而变化,表明所设计的扰动观测器对系统内部参数扰动能够进行有效估计。

图6为参数失配下2种控制策略的相电流傅里叶分析结果。可以看出传统TV-MPCC的定子相电流总谐波畸变率(total harmonics distortion,THD) 为6.80%,而NTV-MPCC的定子相电流THD仅为4.05%。

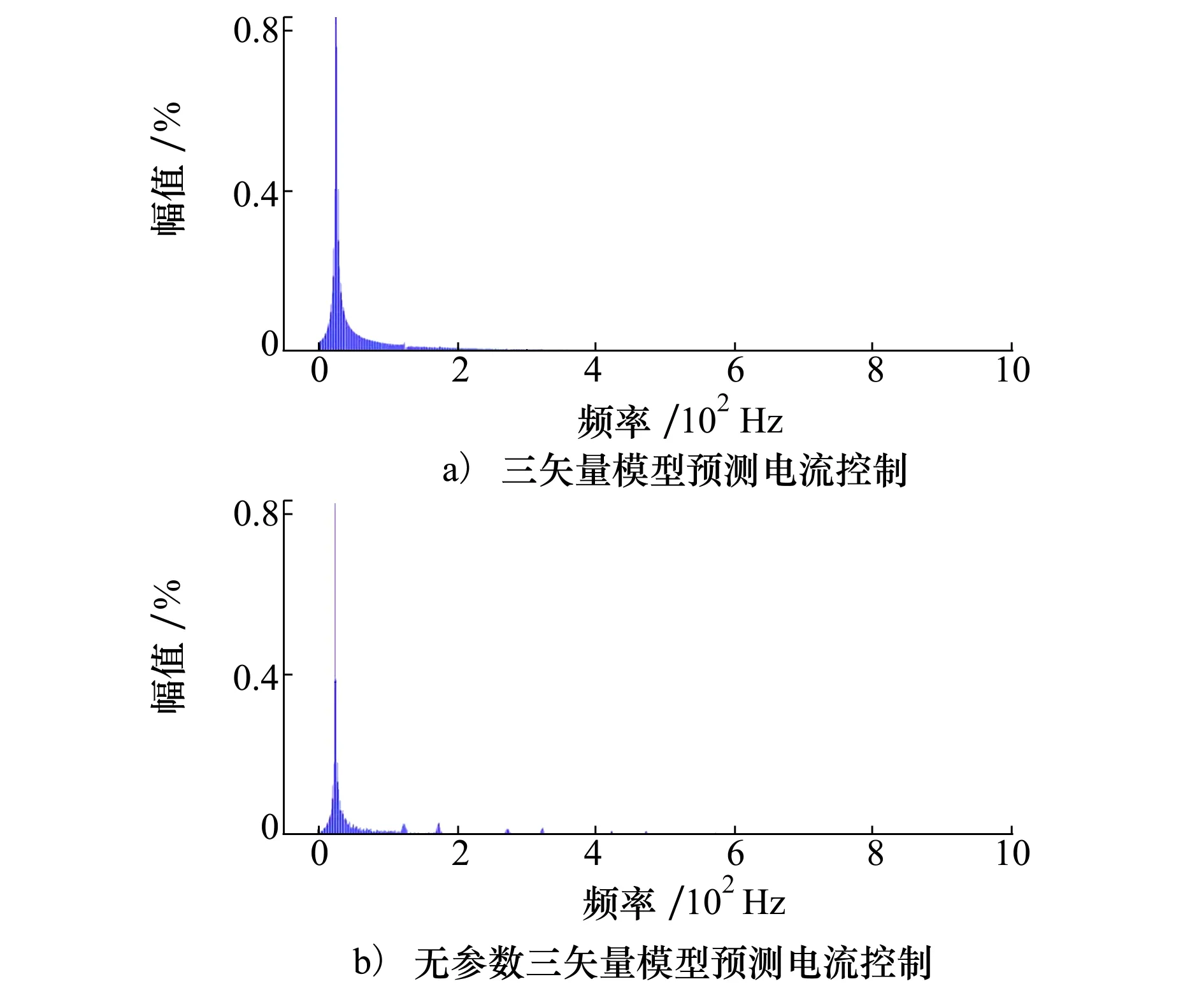
图6 参数摄动情况下A相电流THD分析对比图

由仿真结果可知,在电机参数摄动时,所提NTV-MPCC能对参数扰动进行准确估计并加以补偿,保证了电机的稳态运行性能。而传统TV-MPCC控制下的电机产生了d-q轴电流稳态误差增大以及偏离参考值的情况,影响了电机的稳态性能。

4 实验验证

图7为基于半物理仿真系统SP2000的PMSM实验平台,电机参数同表1。采样频率为10 kHz。实验数据通过上位机存储至MATLAB中进行分析。

图7 PMSM实验平台

为验证电机参数失配时算法的鲁棒性,首先进行参数失配稳态实验。针对传统TV-MPCC,将SP2000控制器中d-q轴电感和定子电阻分别设置为0.5(Ld,Lq),2Rs和2.0(Ld,Lq),2Rs进行参数失配实验。对于所提NTV-MPCC,将超局部模型中的电压、电流系数偏离最优先验值,分别设置为Ad=-480,Aq=-200,Bd=60,Bq=24和Ad=-120,Aq=-50,Bd=15,Bq=6。电机转速为1 000 r/min,负载为9.6 N·m。实验结果如图8和图9所示。

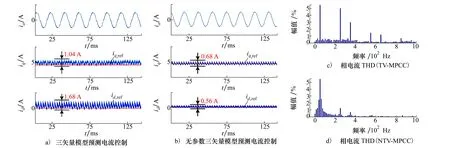
图8 0.5(Ld,Lq)和2Rs下2种策略的电机稳态实验结果

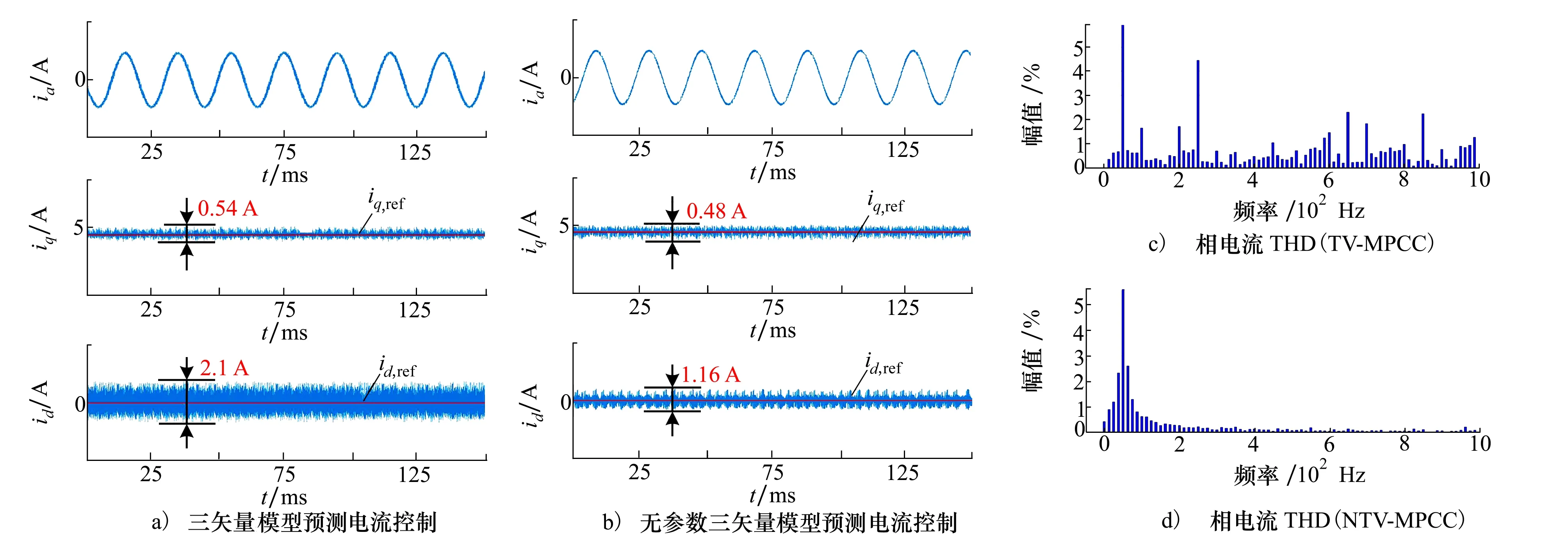
图9 2.0(Ld,Lq)和2Rs下2种策略的电机稳态实验结果

图8为0.5(Ld,Lq)和2Rs下电机稳态响应对比。由图8a)可以看出,传统TV-MPCC的d-q轴电流脉动显著增加,q轴电流脉动约为1.04 A,d轴电流脉动高达1.68 A,且严重偏离参考值。三相电流畸变严重,相电流THD高达8.26%。图8b)为本文所提NTV-MPCC控制下的波形。可以看出,NTV-MPCC的d-q轴电流稳态误差和电流脉动均较小。q轴电流脉动约为0.68 A,相较于传统有参数TV-MPCC,稳态精度提升了大约34.6%;d轴电流脉动仅为0.56 A,稳态精度大约提高了66.67%。三相电流波形正弦度良好,相电流THD仅为6.37%。

图9为2.0(Ld,Lq)和2Rs时的电机稳态波形图,由图9a)可以看出,传统TV-MPCC的d轴电流稳态误差显著增大,d轴电流脉动高达2.1 A左右。同时三相电流高频谐波含量增加,相电流THD高达11.35%。图9b)是NTV-MPCC的实验波形,可以看出稳态性能良好,d轴电流脉动仅为1.16 A,相电流THD约为5.61%,稳态精度提升了50%左右。d-q轴电流误差和三相电流的谐波都显著小于传统TV-MPCC,证明了所提策略的有效性。

为验证NTV-MPCC在电机参数未摄动时的控制性能,与传统TV-MPCC进行实验对比,结果如图10所示。实验中,电机转速指令设为1 000 r/min,带载4 N·m运行,一段时间后负载增至9.6 N·m。

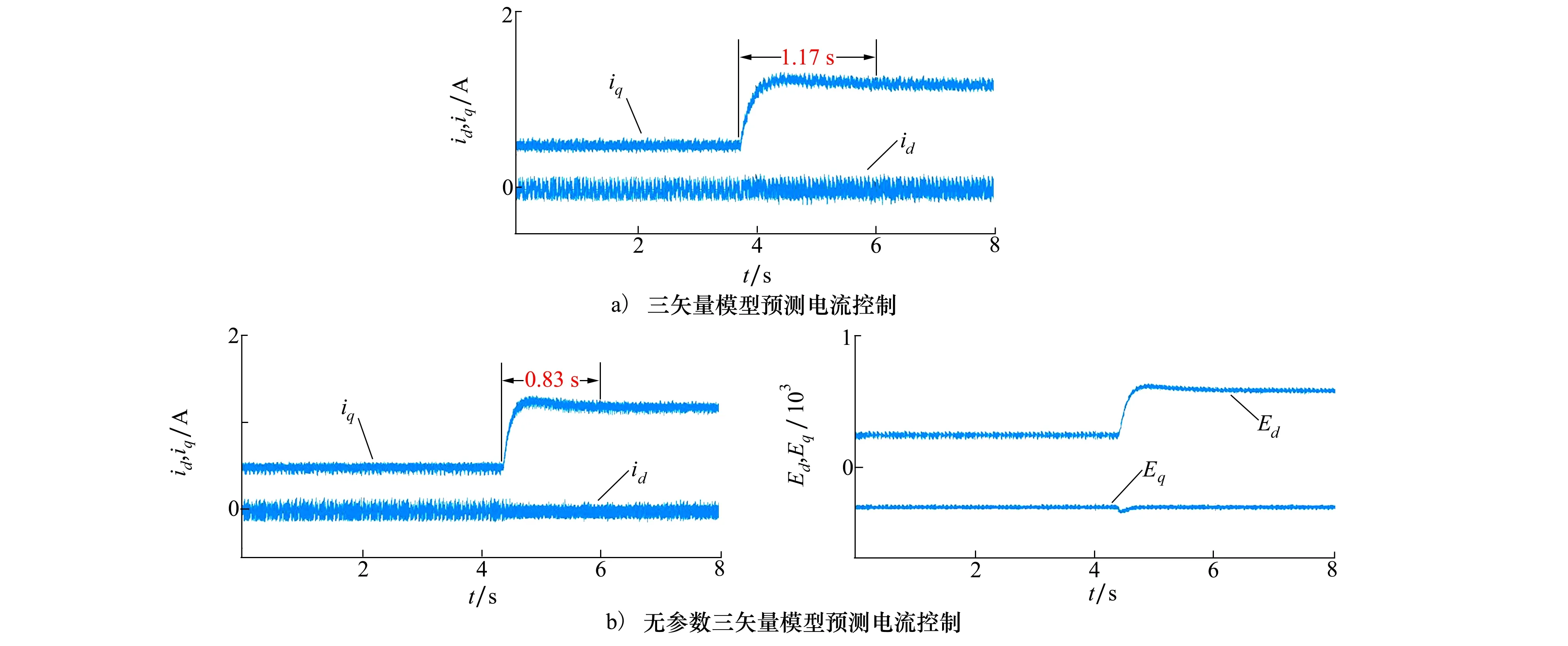
图10 电机参数未摄动时加载波形对比图

由图10可看出,负载从4 N·m增至9.6 N·m后,传统TV-MPCC经过1.17 s后达到稳态,而NTV-MPCC仅用时0.83 s,且加载后的d轴电流稳态误差略小于TV-MPCC。可见NTV-MPCC虽然没有依赖电机参数建立电流预测模型,但在电机本体参数未摄动情况下的动、稳态性能均优于传统TV-MPCC。

仿真和实验结果均可以看出NTV-MPCC策略能有效抑制多矢量模型预测控制易受电机本体参数影响的问题。而实验和仿真结果的差异主要表现在电流脉动的大小,经计算,实验的电流脉动值比仿真的电流脉动值高5倍左右,这主要是由仿真建模的电机,忽略了铁芯饱和、涡流和磁滞损耗等实际因素,以及实际实验过程中控制算法运算时间较长所带来的影响。但从总体控制效果和2种方法对比结论来看,这种误差并不影响研究的总体结论。仿真和实验二者均能充分证明本文所提新策略的有效性和鲁棒性。

5 结 论

针对PMSM传统有参数TV-MPCC对电机本体参数敏感、鲁棒性较低的问题,本文提出一种NTV-MPCC。所提策略构建不依赖电机本体参数的超局部电流预测模型,抑制了电机参数的变化及不确定性扰动对预测电流的影响。引入了基于电流误差的占空比直接计算法,使得占空比计算不受电机本体参数摄动的影响。并提出一种简化的电压矢量组合选择机制,减少了算法的硬件负担。仿真和实验结果表明:在电机参数未摄动情况下,所提NTV-MPCC与传统TV-MPCC具有相似的暂稳态性能;而在电机参数不匹配的情况下,NTV-MPCC方法的稳态性能都显著优于传统TV-MPCC方法。