入水管参数对船载养殖舱流场特性的影响
2023-11-21郭黎明王志陈楚瑶
郭黎明 王志 陈楚瑶
(1 上海和创船舶工程有限公司研发部,上海 200135;2 上海海事大学海洋科学与工程学院,上海 200135)
中国是世界上最大的水产养殖国,水产养殖产量占世界总产量的70%左右[1],但传统水产养殖业仍存在着耗水量大、尾水排放污染、病害严重、滥用药物等问题[2]。近年来,根据循环水养殖体系的优势,在国内外开展了水产养殖业的研究和实践[3]。封闭的工厂化生产方式对仪器设备的依赖程度很高,而养殖舱是可移动式养殖工船的关键设施,因此,构建适宜的养殖舱流场环境是实现高效养殖的重要保障[4-5]。目前养殖舱的设计及优化在国内尚未引起足够的重视,养殖舱内流场的研究更是少有涉及[6]。在养殖舱流场特性的相关研究中,Oca等[7]结合ADV(流速仪传感器)和数学分析法,针对圆形养殖舱内水体的速度分布提出了一个数学模型。该模型可以拟合流量、入水管直径和水深,以获得圆形养殖舱的最佳流速和均匀的流场。Gorle等[8]利用CFD(计算流体动力学)技术开发养殖舱流体动力学的计算模型,以模拟养殖舱中的流场,并区分相对较小和较大养殖舱的物理特性,研究结果给出了包括速度、涡流和湍流在内的舱内流场分布;此外他们还研究模拟了一个大型八角形循环水养殖舱的水流速度分布,通过ADV模型试验对数值模拟结果进行了验证,表明在低流量进水管中加入一个径向流量可以提高养殖舱的整体水动力性能[9]。于林平等[10]从养殖舱几何形状优化和进出水装置改进等多方面开展研究,以改善养殖舱系统的水动力特性和集排污性能。Føre[11]建立了一个模型来估计物理参数变化对鲑鱼生长性能的影响。该模型通过对不同尺寸养殖舱的研究试验数据进行验证,能够预测不同养殖舱规模的影响。
本文基于CFD技术模拟分析养殖舱的流场特性,并对入水管的数量、距池壁的距离、入射角度等参数对流场结构的影响进行探讨,通过对比养殖舱内流场的平均速度和均匀程度来探寻最优入水管的布置方案,以提供适宜养殖鱼类的生长环境,并为船载养殖舱的设计提供参考依据。
1 计算模型的建立
1.1 理论方法
(1)湍流控制方程
湍流是一种普遍存在的流动,其基本特征是多物理尺度和数学非线性,实际的水流流动大多可以认为是湍流流动,因此在进行数值模拟时需要选取适当的湍流模型[12]。RNGk-ε模型是对标准k-ε模型的改进,修正了湍流黏度,考虑了平均流动中的旋转和旋流流动情况,并在ε方程中反映了主流的时均应变率[13]。与标准k-ε模型相比,RNGk-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动[5]。因此本文所采用的湍流模型为RNGk-ε模型。该模型连续性方程和动量守恒方程用张量的指标形式表示如下。
连续性方程:
(1)
动量守恒方程:
(2)

RNGk-ε模型湍流动能和耗散率方程分别为
YM
(3)
(4)
式(3)~(4)中,Gk是由平均速度梯度引起的湍动能k的产生项;Gb是由浮力引起的湍动能k的产生项,对于不可压缩流体,Gb=0;YM表示可压缩湍流脉动膨胀对总耗散率的影响,对于不可压缩流体,YM=0。在FLUENT中,作为默认值常数,C1ε=1.44,C2ε=1.92,C3ε=0.09,αk和αε分别是湍动能k和耗散率ε的有效湍流普朗特数的倒数。
(2)自由液面捕捉方法
水汽交混自由液面应用VOF(volume of fluid)方法进行捕捉,VOF模型适用于处理分层或自由表面这样的问题[14-15]。VOF方程为:
(5)
当C=1时,网格充满流体A,为流体网格;当C=0时,为空网格;当0 (1)船载养殖舱模型 根据CAD图纸提供的参数,在Solidworks 2018中建立养殖舱包括内部入水管的几何模型,几何模型的详细参数在下文进行介绍。船载养殖舱布置见图1。如图1所示,整艘船载养殖舱共设置18个养殖舱,从船艉至船艏分别编号为1 ~18号,其中1号至14号养殖舱几何尺寸相同,15号至18号受船艏影响,外形和尺寸进行了调整。为了使研究结论具有普遍性,对船舯附近的7号养殖舱进行流场分析,7号养殖舱的位置见图1,其内部布置见图2。7号养殖舱为八角形,其内侧沿船长、船宽和深度方向的长度分别为15.34 m×16.60 m×17.00 m。为了收集沉积的饲料和鱼粪等固体残渣,养殖舱底部(图2中红色壁面)是坡度为2°的斜坡,以便于颗粒物向底排口集中。 图1 船载养殖舱布置图 图2 7号养殖舱水动力计算模型 (2)入水管和出水管模型 在养殖舱内设置进水管和出水管,并在管上开孔(见图3~4)。参考国内外研究现状可知,养殖舱进水管需要对称分布才能获得较好的循环流场,如果只在一侧安装1根或2根进水管,无法充分搅动养殖舱内部水体流场,导致进水口远端的流场速度较低,不适宜鱼类生存。根据养殖舱八角形结构的特点,在舱内对角线处对称安装2根或者4根进水管,使流场分布更为均匀,也有利于鱼类养殖作业。因此,本研究在养殖舱内设置2根或4根入水管,入水管直径为630 mm,沿长度方向均匀开设33个孔(出水口),入水管的安装位置、角度以及出水口孔径将在后文进行探讨。根据流量和开孔面积参数,初始布置4根进水管时养殖舱换水速度为1.52 m/s。出水口则由顶部排水口、中间排水管上的出水口及底排水口组成,其中顶部排水口的流量占总流量的30%,中间出水口及底排水口的排水量占总流量的70%。 图3 进水管网格分布情况 图4 出水管和底排水口网格分布情况 将建好的几何模型转换为IGS格式文件,并导入Ansys ICEM CFD软件中划分网格,网格分布见图2~4。整个流场内部采用四面体网格划分,入水口和出水口等尺寸较小的区域将网格进行加密进而提高计算精度。养殖舱流动空间内的网格数量为287万,入水管表面网格数为10.7万,入水口网格数为1.4万,出水口网格数为5.6万,中间管出水口网格数为1.5万,底排水口网格数为0.3万。 本研究中的养殖舱边界条件设置如下:入水口设为速度入口,入口速度根据入水口的直径和流量进行确定;出水口设为压力出口;假设水面无剪切和滑移速度,当作自由界面处理,压力值为大气压;池底和池壁为固体壁面边界,采用标准壁面函数;池顶为自由液面。计算过程中,压力速度耦合方式采用SIMPLE的方法,湍流动能采用一阶迎风离散模式[16]。 对网格的独立性进行验证,排除网格密度对养殖舱流场模拟结果的影响。划分3组不同密度的网格模型,分别命名为Mesh-coarse、Mesh-medium和Mesh-fine。舱室网格尺寸依次减小25%,对应的网格数量分别为128万、287万和644万。 采用前文介绍的方法对初始布置方案的养殖舱进行水动力分析,将3组网格计算的流场平均速度结果进行对比。由于养殖舱内的水流循环方向与水平面平行,且后文将对不同水深位置的流场进行对比,因此,本研究选取3种不同水深(2 m、7 m和12 m),对其平面处的平均速度和速度分布情况进行网格无关性分析。网格无关性验证结果见表1。 表1 网格无关性验证中不同水深处的平均速度 从计算结果中可以看出,网格密度对计算结果有一定的影响。由Mesh-coarse加密到Mesh-medium的过程中,平均速度变化较大,因此需要进一步加密。由Mesh-medium继续加密到Mesh-fine的过程中,网格数量增加了2.24倍,而不同位置处的流速变化均在1%左右。成倍加密网格带来了巨大的计算量,但是对计算结果影响较小,因此,后文均采用Mesh-medium的网格密度来进行养殖舱流动数值分析。 为了分析入水管布置方式对养殖舱流场的影响,本文对入水管数量、入水管与池壁距离和入水口开孔角度等参数进行分析,具体入水管入射角度和位置见图5,具体分析工况见表2。为了能够对比2根和4根入水管工况的流场情况,将2根入水管的口径改为4根入水管口径的1.414倍,也就是14.14 mm,这样处理后所有入水管的射流速度均为1.52 m/s。 表2 入水管参数 图5 入水管入射角度和位置示意图 2.2.1 计算结果的整理 为了分析以上入水管参数对流场的影响,文中计算了所有工况的流场,并对比了水深5 m处的流速分布,结果见图6~7。 图6 采用2根入水管的养殖舱速度分布(水深5 m处) 由图6~7可以看出,入射角度在22.5°~45°范围内,随着入射角度的增大,养殖舱内流场低速区逐渐减小,个别工况增加到一定程度时流场变得紊乱。当入射角度在30°~35°时,入射流将与舱内水体运动的切线方向形成一个夹角,切线方向上的水体与池壁相互作用,产生能量损失,使得流体的切向速度降低,入射流逐渐转向,驱使中心区域的流体旋转,破坏了流场的混合均匀性。为了分析入水管数量、池壁距离以及开孔角度3个参数对流场分布的影响,本文保持其他两种变量不变,单独分析某个参数对养殖舱内水体循环情况的影响。 2.2.2 入水管数量对养殖舱流场的影响 选取入水管距池壁2 900 mm、开孔角度为35°时的养殖舱,比较入水管分别为2根和4根时的养殖舱流场,养殖舱中纵剖面处的速度分布见图8。 结合图8结果和图7中对应的工况结果可以看出,在布置2根入水管的养殖舱内,显示为深蓝色的低速区范围较小,而布置4根入水管的养殖舱内流速小于0.1 m/s的区域范围更大。通常大范围的低速区不适合进行鱼类养殖,因此,在本研究的参数范围内,布置2根入水管的养殖舱流场更优。 图8 不同入水管数量的中纵剖面速度分布情况(左为2根,右为4根) 2.2.3 入水管与池壁的距离对养殖舱流场的影响 确定入水管数量后,将开孔角度设置为35°,分析入水管距池壁的距离对养殖舱流场的影响,养殖舱中纵剖面处的速度分布如图9所示。 由图9和图7中对应的工况结果可以看出,随着入水管与池壁距离的增加,流场中央的低速区逐渐变小,当与池壁的距离为3 400 mm时,低速区最小。继续增加距离,流场低速区反而增大。因此,在一定条件下,入水管与池壁的距离有最优布置情况,对比分析结果,入水管距离池壁3 400 mm时流场最优。 2.2.4 开孔角度对养殖舱流场的影响 确定前两个参数后,再对开孔角度进行对比,养殖舱中纵剖面处的速度分布如图10所示。 由图10和图7中对应的工况结果可以看出,随着开孔角度的增加,养殖舱内的低速区逐渐减小,当开孔角度为35°时,舱内流场最为均匀。继续增加开孔角度,入水口的射流互相影响,使养殖舱内流场混乱,不利于鱼类养殖,因此,开孔角度为35°时流场最优。 为了更合理地选择入水管的布置方式,对几种工况的平均速度和标准差进行对比,分别绘制成散点图和表格。在不同工况下流场平均速度变化情况见图11,标准差见图12。 图11 入水管与池壁不同距离时的流场平均速度变化情况 图12 不同池壁距离下流场速度的标准差结果 由养殖舱内平均流速、标准差和流场云图综合分析得出,当入水管距池壁距离由1 900 mm增大到3 400 mm时,舱内水体逐渐呈现离心运动状态,邻近舱壁的水体逐渐呈现向中心运动的态势,水体由离心运动状态逐渐变为环流运动(与舱壁几何形状有关),水体质点间的能量消耗占比减小,舱内水体混合均匀性明显改善;当入水管与池壁的距离从3 400 mm增大到3 900 mm时,水体质点间的非规则运动及相互摩擦产生的能量损失导致养殖舱中间区域出现大面积低流速区,舱内水体混合均匀性逐渐变差,养殖舱的利用率降低。 平均速度体现了养殖舱内整体速度的情况,当出现流场紊乱的情况,平均速度会迅速下降;而标准差体现了养殖舱内流场速度的均匀程度,标准差结果越小,流场越均匀。对比计算结果发现,入水管数量、与池壁的距离以及入射角度都影响流场的平均速度和标准差。减少流场与池壁间的摩擦和入射水流之间的干扰,能够减小流体动能的损失,流场速度也会更平均;当不同位置速度差异变小后,流场速度的标准差也随之减小。对比采用4根和2根入水管的养殖舱,2根管的平均速度更高,标准差更小,且2根入水管的安装布置更为简单。 增大入水管与池壁的距离能够提高养殖舱的平均速度并降低标准差,当与池壁的距离从1 900 mm增大到2 900 mm或3 400 mm时,流场平均速度达到最大值,此时标准差也达到最小值。 增加入射角度也可以提高养殖舱流场的平均速度并降低标准差,当入射角度增加到30°或35°时,流场平均速度达到最大值,此时标准差也达到最小值。 根据前文分析结果可知,当采用两根入水管、入水管距池壁3 400 mm、入射角度为35°时,养殖舱流场分布较为合理。确定好养殖舱入水管的布置方式后,还需要确定养殖舱换水速度(入水管射流速度)对流场的影响,同时观察液面的变化情况。其中1倍、2倍和3倍流量分别对应的入口射流速度为1.52 m/s、3.04 m/s和4.56 m/s,同时底排水的速度也随之成倍增加。不同流量下养殖舱对称面内液面状态和速度矢量结果见图13。 从以上结果可以看出,当底排水速度增加到一定程度后能够产生水面漩涡。增大底排水流速的方式是提高养殖舱内的流量,当入水管流速成倍增加后,底排水的流速也相应地成倍增加,当底排水流速增大到200%时,流场速度分布发生改变,液面产生轻微的凹陷,养殖舱中心位置出现漩涡,流场速度矢量产生旋转,出现类似“龙卷风”的结构,速度场中心处出现类似“暴风眼”的低速区。当底排水流速增大到300%时,这种漩涡的规模和强度继续增加,液面出现明显的凹陷,漩涡的旋转速度远超流场其他位置的速度,不同高度的中心在水平位置发生摆动,使之更像“龙卷风”。这种流场分布不利于鱼类养殖,因此设计养殖舱流量时一定要考虑流场是否会出现漩涡。 目前大多数船载养殖舱的深度相比宽度较小,大深度养殖舱的相关研究较少。本文采用CFD方法分析了不同入水管的布置方式对船载养殖舱流场的影响,得出以下研究结论: (1)流场模拟结果表明,养殖舱壁面处的水流速度最大,舱内流速分布由舱壁向中心逐渐减小。养殖舱中心存在流动较慢的低速区,随着进水流速的增大,低速区域的面积逐渐减小,但不会消失,舱体中心小面积的低速区可有效防止固体颗粒物受扰动后重新悬浮,但若该区域逐渐扩大,会降低养殖舱的利用率和排污能力。出现低速区的主要原因是:水体质点与舱壁摩擦造成的能量损失。 (2)选择合理的进水管布置,可以在满足养殖需要的同时优化养殖舱流场。由流场速度分布特征图可以看出,采用2根(双管间隔式)入水管布设舱底,流场平均速度更高,标准差更小,养殖舱壁面处的低流速区占比小,流场分布更加均匀。双管间隔式进水保证了流场水流均匀,有利于二次流的形成,可以促进鱼类粪便等固体废弃物的汇聚,且两根管的布置更简单。其余工况下,养殖舱的倒角和边壁处均会出现环流运动和大面积的低速区。 (3)增大入水管与池壁的距离能够提高养殖舱流场平均速度并降低标准差。当入水管距池壁3 400 mm时,水体质点与舱壁摩擦消耗的能量占比逐渐降低,舱内水体用于维持环流运动和离心运动所需要的能量增多,舱内能量足以忽略水体离心运动时质点间相互撞击产生的能量损失,舱内水体的均匀性得到改善,养殖舱水体质点呈现稳定平衡的规则质点运动,舱内高低流速区分布稳定,流场整体流速较高且流体混合均匀。 (4)降低养殖舱由入射水流与舱壁撞击所产生的能量消耗是优化养殖舱流场特性的有效方式。当入射角度在22.5°~35°时,水流平均速度随着入射角度的增加而逐渐增大;当入射角度在35°~45°时,水流平均速度随着入射角度的增加而逐渐减小。当入射角度为35°时,养殖舱内平均流速达到最大,此时标准差也达到最小值。 (5)提高底排水速度能够产生液面旋涡。当底排水流量增加到设计工况的2倍时,液面会出现凹陷,流场中心处出现漩涡结构,漩涡外围速度大小超过流场其他位置的速度;继续增加底排水流量,漩涡沿水深方向发生摆动。 本研究旨在为船载养殖舱流场分析提供一种新的研究思路,未来将会通过实船测量进一步验证本文研究结果的可靠性。1.2 养殖舱模型的建立




1.3 网格划分与边界条件设置
1.4 网格无关性验证

2 结果与分析
2.1 计算工况介绍


2.2 不同参数对养殖舱流场的影响
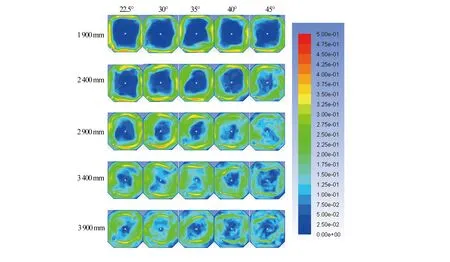

2.3 养殖舱入水管最优布置方式分析

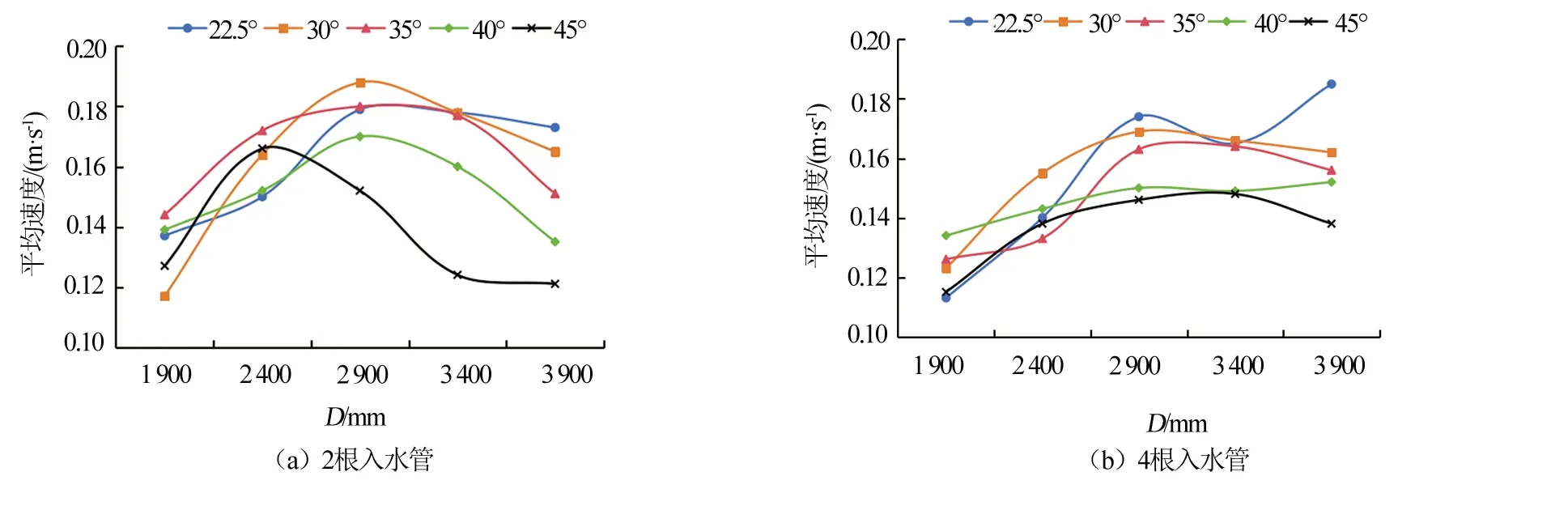
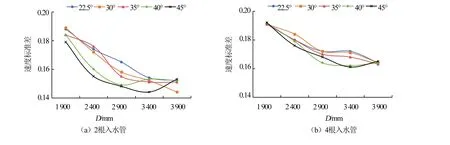
2.4 入水管流速对养殖舱流场的影响
3 讨论
