不确定分数阶超混沌Tang系统的有限时间滑模同步
2023-11-20杨喜平毛北行
杨喜平,毛北行
(郑州航空工业管理学院 数学学院,河南 郑州 450015)
滑模方法由于其良好的鲁棒性能被广泛应用于自动化、控制、通信、生化、医疗、化工等学科领域[1-3],相关混沌系统滑模同步控制方法的研究已经取得了丰富的成果[4-8].文献[9]基于滑模方法研究不确定非线性动力系统控制问题,并对系统的动力学行为进行了详细分析.文献[10]研究不确定超混沌Bao系统的积分滑模同步问题,给出了滑模面的设计.文献[11]基于自适应方法研究分数阶不确定Victor-Carmen系统的滑模同步,设计了控制器和自适应控制律.文献[12]研究超混沌Bao系统自适应滑模同步,得到超混沌Bao系统滑模同步的充分条件.随着人们对分数阶系统的深入了解,众多学者开始认识到实际系统都可以用分数阶微分方程来建立数学模型且更符合模型本身,因而该方面的研究备受关注.文献[13]研究分数阶新超混沌系统滑模同步的4种方法,给出滑模面的选取及控制器的设计.文献[14]研究分数阶不确定非线性Sprott混沌系统的滑模同步,给出了滑模函数的设计.另外系统建模时必须考虑不确定因素带来的影响,且大多数情况下实际的控制系统都要求系统能在有限时间内取得同步,即 “有限时间同步”.文献[15]研究不确定Victor-Carmen系统有限时间滑模同步.文献[16]研究不确定临界系统的有限时间滑模同步.而Tang混沌系统自2009年被提出以来就备受关注.文献[17]研究3阶Tang混沌系统的动力学行为等特性.文献[18]研究超混沌Tang系统的吸引性及电路实现.另一方面分数阶不确定超混沌Tang系统的有限时间滑模同步问题还没有被系统地研究过,基于以上研究,论文考虑不确定分数阶超混沌Tang系统的有限时间滑模同步问题,得到不确定分数阶超混沌Tang系统有限时间滑模同步的充分性条件.
1 系统描述
Tang系统[17]状态方程可描述为
(1)
当a=25.6,b=66.8,c=39.22,d=0.2,k=4时,系统呈现吸引子特性,其吸引子相图如图1所示.
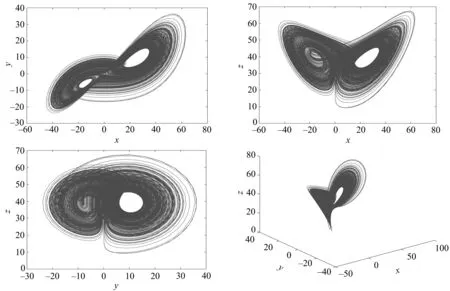
图1 Tang系统的吸引子相图
将上述系统增加一个非线性项,得到新的超混沌Tang系统[18],具体可描述为
(2)
当a=20,b=35,p=1,c=30,d=5,k=16时,系统呈现超混沌特性,吸引子相图如图2所示.
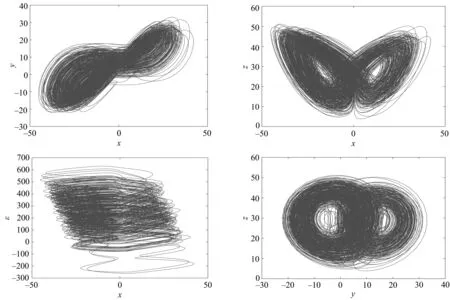
图2 超混沌Tang系统的吸引子相图
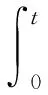
定义1[19]Caputo分数阶导数定义为
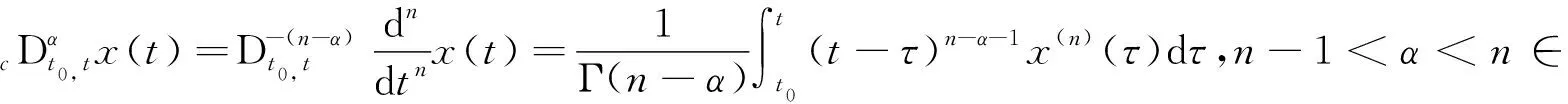
引理1[19]若x(t)为连续可微的函数,则对任意的t≥0,有
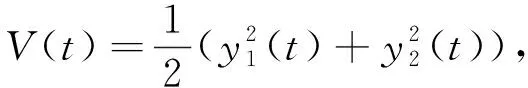

(1)α1‖x(t)‖a≤V(t,x(t))≤α2‖x(t)‖ab;
(2)kV1/β(t,x(t))≤α3‖x‖ab;


以下考虑分数阶超混沌Tang系统
(3)
当a=20,b=35,p=1,c=30,d=5,k=16,q=0.987时,系统出现超混沌吸引子,吸引子相图如图3所示.

图3 超混沌分数阶Tang系统的吸引子相图
以系统(3)为主系统,设计从系统为
(4)
其中:Δfi(y)为不确定项,di(t)为有界外扰,ui(t)为控制器,y=[x1,y1,z1,ω1]T.
假设1设不确定项Δfi(y)和外部扰动di(t)有界,即存在未知参数mi,ni>0,使得
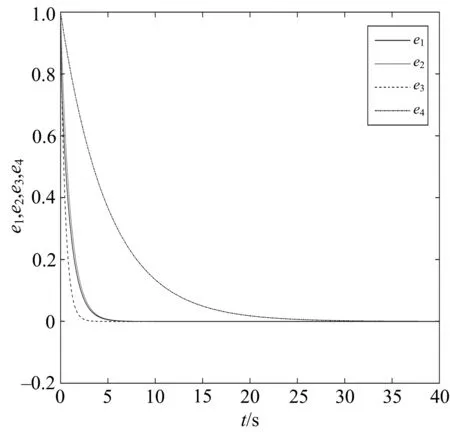
|Δfi(y)| 定义e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,得到误差系统方程 (5) 定理1假设1条件下,设计滑模面si(t)=ei(t)+λiDt-q|ei(t)|θsgn(ei(t)),0<θ<1,控制器 自适应规则 根据不等式 ‖x1‖p+‖x2‖p+‖x3‖p+‖x4‖p≥ 取λ=min{λ1,λ2,λ3,λ4},有 根据引理3,化简后得 λ1|e1(t)|θsgn(e1(t))]+s2[ce1-x1z1+xz-e2+Δf2(y)+d2(t)+u2(t)+ λ2|e2(t)|θsgn(e2(t))]+s3[x1y1-xy-d(e1+e3)+Δf3(y)+d3(t)+u3(t)+ λ3|e3(t)|θsgn(e3(t))]+s4[k(e1+e2)+Δf4(y)+d4(t)+u4(t)+λ4|e4(t)|θsgn(e4(t))]+ 作为分数阶系统的特例,以整数阶系统(2)为主系统,设计从系统如下 (6) 定义e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,得到误差系统方程 (7) V1-η(t)≤V1-η(t0)-p(1-η)(t-t0),t0≤t≤T, 自适应规则 根据不等式 取λ=min{λ1,λ2,λ3,λ4},有 不在滑模面上时,构造 s1[-ae1+be2-pe4+Δf1(y)+d1(t)+u1(t)+λ1|e1(t)|θsgn(e1(t))]+ s2[ce1-x1z1+xz-e2+Δf2(y)+d2(t)+u2(t)+λ2|e2(t)|θsgn(e2(t))]+ s3[x1y1-xy-d(e1+e3)+Δf3(y)+d3(t)+u3(t)+λ3|e3(t)|θsgn(e3(t))]+ s4[k(e1+e2)+Δf4(y)+d4(t)+u4(t)+λ4|e4(t)|θsgn(e4(t))]+ 其中:k=min{k1,k2,k3,k4},上式两边积分得 取a=20,b=35,p=1,c=30,d=5,k=16,q=0.987,(x(0),y(0),z(0),ω(0))=(3.2,8.5,3.5,2), Δf1(y)+d1(t)=0.1sin(t)x1+0.1cost,Δf2(y)+d2(t)=-0.1cos(t)y1+0.1cost, Δf3(y)+d3(t)=-0.1sin(t)z1+0.1cos(2t),Δf4(y)+d4(t)=0.1cos(t)ω1+0.1sint. 定理1中选取滑模面 si(t)=ei(t)+λiDt-q|ei(t)|θsgn(ei(t)),0<θ<1, 定理2中选取滑模面 定理1,2中的误差曲线如图4,5所示.从图4,5中可以看出,初始时刻误差相差较大,且系统误差距离坐标原点较远,随时间变化误差逐步趋向一致,并且逐渐向坐标原点趋近,说明系统达到同步.另外文中讨论的问题虽然是分数阶,但对于整数阶系统也同样成立.论文所使用的方法对整数阶、分数阶系统均具有适用性和可移植性. 图4 定理1中的系统误差曲线 图5 定理2中的系统误差曲线 根据有限时间滑模同步控制理论研究不确定分数阶超混沌Tang系统的同步,通过构造滑模函数和控制器及自适应规则,获得分数阶不确超混沌Tang系统取得有限时间滑模同步的充分性条件,结论不仅对分数阶系统成立,对整数阶同样适用,并用数值仿真验证了所得结论.如何设计出更加简洁的滑模面,使系统误差能够快速收敛到原点,是作者下一步需要考虑的问题.2 主要结果
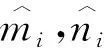
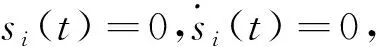
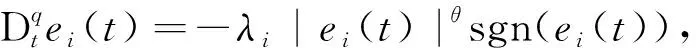
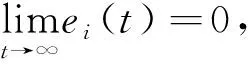

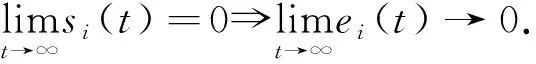



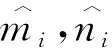
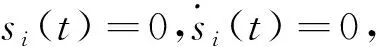
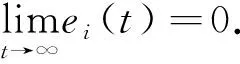
3 数值仿真
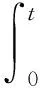

4 结束语
