模型无关元迁移学习用于空间滚动轴承寿命阶段识别

李统一，李 锋，汤宝平，汪永超

（1.四川大学机械工程学院，四川 成都 610065；2.重庆大学机械传动国家重点实验室，重庆 400044）

引言

空间飞行器的机械部件能否正常运转、实现预定功能和达到预期服役寿命，很大程度上取决于飞行器中各机械部件内滚动轴承的寿命和可靠性。由于空间在轨环境中难以获取轴承运行状态信息，空间环境与地面常规环境之间存在较大区别，处于空间环境下的滚动轴承要承受微重力、高真空、高能粒子辐照、高低温交变等极端恶劣环境的影响，地面常规环境测试得到的滚动轴承运行特性并不能全面反映滚动轴承在空间环境下的运行性能［1］。为保证安装到空间飞行器中的滚动轴承具有良好状态，目前国内外相关研究机构包括欧洲航天局、美国国家航空航天局等通常采取在地面模拟空间环境开展空间滚动轴承寿命鉴定试验来识别空间滚动轴承的寿命阶段，再对被识别为正常状态（即未产生精度失效）的空间轴承进行剩余寿命预测，以实现从大量的候选空间滚动轴承中筛选出最优寿命（即剩余寿命较长）轴承安装到空间飞行器中。

在地面模拟空间环境下，空间滚动轴承的失效一般是由于固体润滑膜的磨损造成的精度失效，相比于典型故障或早期故障状态，其有效寿命阶段内的振动特征更为微弱。其次，模拟空间环境的设备（如真空泵）空间狭小，多组轴承同时试验，导致空间轴承振动信号受到强烈的环境噪声干扰，这些干扰成分与空间轴承真实振动信号的低频段分量混叠、耦合。空间滚动轴承一般工作在变工况（即变加速应力）下，模拟空间环境下的滚动轴承往往采取径向无加载、轴向加载方式开展加速寿命试验，轴承振动受轴向载荷大小影响明显，随着轴承磨损，轴承间隙改变，轴向载荷将发生持续性的变化。同时，由于真空室容量的限制，难以实施电机转速的闭环控制，轴承转速存在波动［1-2］。以上地面模拟空间环境下空间滚动轴承加速寿命试验的特殊性使空间滚动轴承的运行、退化和失效过程与地面常规环境下的传统滚动轴承有明显差异，导致地面模拟空间环境下空间滚动轴承寿命阶段识别具有较大的挑战。

目前地面模拟空间环境下空间滚动轴承寿命阶段识别的研究刚刚起步，有为数不多的研究案例。如：陈仁祥等［1］采用线性局部切空间排列算法（Linear Local Tangent Space Alignment，LLTSA）和最近邻分类器（K-Nearest Neighbors Classifier，KNNC）相结合的方法进行模拟空间环境下航天轴承不同寿命阶段的识别；Dong 等［2］结合沙利斯熵KPCA（Tsallis Entropy-KPCA，TE-KPCA）和优化模糊C均值模型（Optimized Fuzzy C-means Model，OFCM）进行模拟空间环境下空间滚动轴承寿命阶段识别；Miao 等［3］采用支持向量机（Support Vector Machine，SVM）和模糊逻辑推 理（Fuzzy Logic Inference，FLI）来进行航空轴承寿命状态预测。然而，以上涉及到的机器学习方法都是基于概率分布一致性假设，而模拟空间环境下空间滚动轴承加速寿命试验是在变工况条件下进行的，基于分布一致性假设的机器学习方法在变工况条件下泛化能力较差，因此不是特别适用于地面模拟空间环境下的空间滚动轴承寿命阶段识别。以上所有机器学习方法都需要大量的有类标签的历史工况（即源域）数据来进行训练且要求各类训练样本数量必须均等，然而受试验成本和试验周期限制，地面模拟空间环境试验条件下往往仅能获得部分历史工况下的少量空间滚动轴承全寿命样本数据用于分类模型的训练，且空间滚动轴承不同寿命阶段的时间跨度的不均等因素往往造成各个寿命阶段的样本数量也不均等，以上复杂的地面模拟空间环境试验条件也决定了上述机器学习方法用于地面模拟空间环境下空间滚动轴承寿命阶段识别存在一定的局限性。

迁移学习（Transfer Learning，TL）［4-5］为变工况下的空间滚动轴承寿命阶段识别提供了全新解决思路，然而传统迁移学习面对少样本和样本不均等情况时在泛化性能、分类性能等方面仍然存在不 足。元学习（Meta Learning，ML）［6-7］在解决 少样本分类问题和提高网络泛化能力方面有很好的效果，在提高迁移学习网络的迁移性能方面具有潜 力。原型网 络（Prototype Network，PN）［8］在小样本和不同类别样本不均等这两情况下对样本分类的精度都比一般神经网络更高。因此本文结合迁移学习、元学习和原型网络的各自优势，提出了一种新型无监督的迁移学习理论——模型无关元迁移学习（Model-Agnostic Meta-Transfer Learning，MAMTL）用于地面模拟空间环境下空间滚动轴承寿命阶段识别。

1 模型无关元迁移学习

MAMTL 由内环平行网络、外环元学习网络和原型网络组成。内环平行网络和外环元学习网络都由相同的任一迁移学习网络构成。首先借助空间滚动轴承无类标签的源域和目标域样本对内环平行网络进行同步训练得到多任务所有的损失函数；然后通过多任务所有的损失函数的共同作用来训练外环元学习网络得到该网络参数的全局最优解作为该网络参数的初始值，这样使外环元学习网络具有更好的泛化能力；然后用空间滚动轴承目标域无类标签样本和少量的源域有类标签样本来参与训练外环元学习网络，以对外环元学习网络参数进行微调，使外环元学习网络具备小样本跨域迁移学习能力；最后用所构建的新型原型网络作为分类器，通过求空间滚动轴承目标域样本与每一类原型的相似度完成对目标域无类标签样本的类判别（即寿命阶段识别），MAMTL 的结构框架如图1 所示。

图1 MAMTL 的结构框架图Fig.1 Structure frame diagram of MAMTL

1.1 内环平行网络基础学习

每个任务分别在具有相同初始值的内环平行网络中训练。每个内环平行网络由相同的任一迁移学习网络组成，令迁移学习网络的特征映射函数为F(⋅)，该网络的参数集为θ，该网络的分布差异度量函数为G(⋅)。假设第m次训练时外环元学习网络的参数初始值集合为θm，同时将其作为N个任务对应的内环平行网络的参数初始值集合。在任务Ti中，先将支持集样本，输入该任务所对应的迁移学习网络特征映射函数，以分别提取得到高维特征该过程表达如下：

提取到高维特征后，通过分布差异度量函数G(⋅)来构造如下支持集高维特征的损失函数：

通过该损失函数优化迁移学习网络参数以实现源域样本高维特征和目标域样本高维特征分布差异的最小化，进而更好地实现从源域向目标域的跨域迁移。

得到支持集高维特征的损失函数后用随机梯度下降法对该迁移学习网络的参数θm进行一次更新，该更新过程如下：

式中α为内环平行网络参数的学习率；∇θ表示对参数集θ求偏导数。

于是，每个任务分别在对应的内环平行网络内依据式（1）～（4）来更新迁移学习网络参数，得到该任务更新后的内环平行网络参数集

接下来，再用分布差异度量函数来构建查询集高维特征的损失函数，可以得到：

于是，N个任务经过相对应的内环平行网络训练后分别得到N个不同的查询集高维特征损失函数

1.2 外环元学习网络

将N个任务的查询集高维特征损失函数的平均值作为外环元学习网络的总损失函数，该过程可由下式表达：

用得到的总损失函数来优化外环元学习网络的参数集θm，完成一次外环元学习网络的参数更新，该参数优化过程可推导为：

式中β为外环元学习网络参数的学习率。优化得到的参数集θm+1作为下一次训练时内环平行网络的参数初始值集。

重复执行式（1）～（9）所示训练过程，直到将外环元学习网络参数训练至收敛，也就完成了外环元学习网络的预训练。由于外环元学习网络每一次更新的参数都是由内环平行网络中多个任务的所有损失函数共同作用得到的全局最优解，所以以最后更新好的全局最优解（即预训练好的外环元学习网络参数集θn）作为外环元（迁移）学习网络的起始点（即初始值）去学习新的任务时仅需要少量迭代次数就能使外环元学习网络达到收敛，即又好又快地适应新的迁移学习任务，因此预训练好的外环元学习网络具有良好的泛化性能和域适配性。

1.3 MAMTL 的原型网络

然后由以上两组高维特征值的分布差异度量函数来构造外环元学习网络的损失函数L(θn)：

设空间滚动轴承源域和目标域全体样本一共有Q类（即Q个寿命阶段），令Sq表示属于第q类标签的样本，其中q∈1，…，Q，nq表示属于第q类样本的数量。接下来，由源域有类标签样本的高维特征计算每一类的原型，该计算过程如下：

计算目标域待测样本的高维特征与式（13）所示原型的相似度，并选择相似度最大的那一类原型所对应的类标签作为空间滚动轴承目标域待测样本的预测伪类标签，该过程表达如下：

式中d(⋅)表示两个向量之间的相似度函数。

计算该目标域待测样本属于伪类标签qj的概率如下：

接下来，将所有目标域待测样本属于其对应的伪类标签概率的负对数之和作为原型网络的损失函数，该损失函数推导如下：

于是，整合外环元学习网络的损失函数L(θn)和原型网络的损失函数J(θn)来共同构建MAMTL的总损失函数如下：

式中γ为外环元学习网络的平衡约束参数，用于约束外环元学习网络局部寻优行为。使用随机梯度下降法将MAMTL 的总损失函数训练至收敛，完成对外环元学习网络的参数微调，此时得到外环元学习网络对该任务的最优参数θ*，也即完成对MAMTL 的训练。

最后，再将空间滚动轴承源域有类标签样本和目标域待测样本输入训练好的MAMTL 网络，计算出目标域待测样本的类标签（即寿命阶段），以完成元迁移学习全过程，该过程表达如下：

由以上推导可知，为MAMTL 构建的新型原型网络是将源域每一类别中所有的样本用一个原型表示，通过计算目标域待测样本与原型的相似度完成目标域待测样本的分类，这样可以避免因源域不同类别样本数量的差异而造成对不同类别样本分类精度差别过大（即对少样本类别的样本的分类精度过低）问题；同时，在计算目标域待测样本与不同原型的相似度时没有参数学习的过程，所以在训练小样本情况下不会出现过拟合现象。

2 基于MAMTL 的空间滚动轴承寿命阶段识别

所提出的基于MAMTL 的空间滚动轴承寿命阶段识别方法的实现过程如图2 所示：

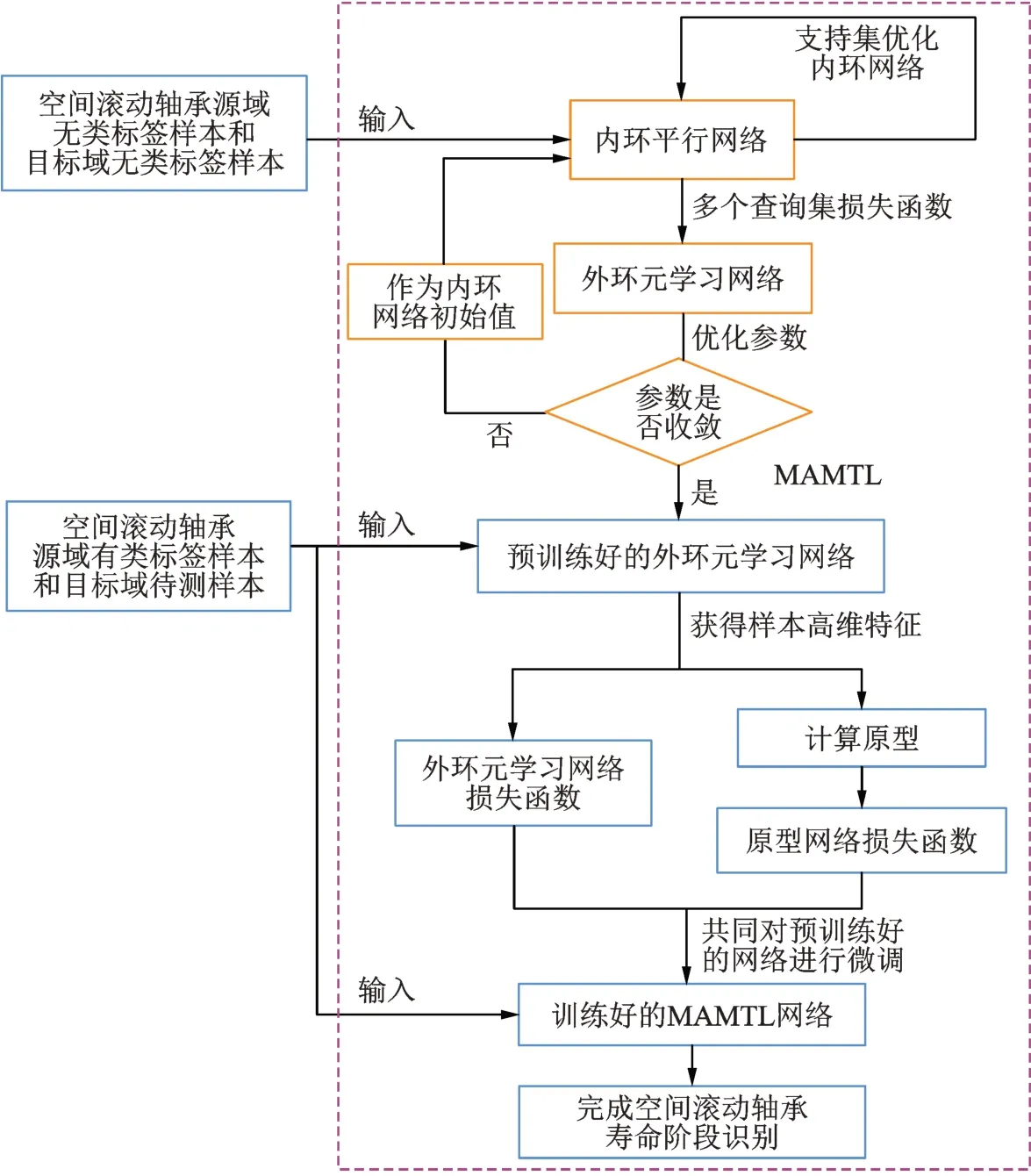
图2 基于MAMTL 的空间滚动轴承寿命阶段识别方法实现流程Fig.2 Implementation process of life stage identification method of space rolling bearings based on MAMTL

（1）选择空间滚动轴承无类标签的源域和目标域样本进行预训练，一次训练为内环平行网络设置N个学习任务，将每个任务的样本分为源域支持集、目标域支持集、源域查询集、目标域查询集。

（2）将每个任务的支持集样本输入与该任务对应的内环平行网络提取到高维特征，然后构建支持集高维特征的损失函数，以优化一次内环平行网络的参数。

（3）将每个任务的查询集输入更新参数后的与该任务对应的内环平行网络中提取高维特征，再将N个任务的查询集高维特征损失函数的平均值作为外环元学习网络的总损失函数用于优化外环元学习网络参数集，完成一次外环元学习网络的参数更新。重复（1）～（3）过程，直到外环元学习网络参数训练至收敛，完成外环元学习网络的预训练。

（4）将空间滚动轴承源域有类标签样本和目标域待测样本输入预训练好的外环元学习网络得到各自的高维特征，进而计算外环元学习网络的损失函数；然后由源域有类标签样本的高维特征得出每个类别的原型；最后计算目标域样本高维特征与每个原型的相似度以得到目标域样本的伪类标签，进而得到原型网络的损失函数。

（5）由外环元学习网络的损失函数与原型网络的损失函数共同构建MAMTL 的总损失函数，将该总损失函数训练至收敛，完成对外环元学习网络参数微调。

（6）用训练好的MAMTL 完成对目标域待测样本的分类，即完成对空间滚动轴承的寿命阶段识别。

3 实例分析

3.1 实验装置

实验数据主要来自自主搭建的空间滚动轴承振动监测（即加速寿命试验）平台上采集的地面模拟真空环境下空间滚动轴承寿命试验数据。该平台如图3 所示，主要由真空泵、轴承振动监测实验台架、压电式加速度传感器、双积分信号调理器、NI 数据采集卡和计算机组成，将型号均为C36018 的空间滚动轴承1 和2 安装于真空泵中的振动监测实验台架上。在真空环境下轴承1，2 均被加载7 kg 的轴向预载（随着轴承磨损加剧，轴向载荷会发生持续性变化），并分别在约1000 r/min 和3000 r/min 的2 种非平稳转速下运行（即表1 中的非稳态工况C1 和C2）。压电式加速度传感器对这两个空间滚动轴承进行振动监测并每隔2 h 以25.6 kHz 的采样频率采集一次它们的振动加速度信号，直至这两个轴承都完全止动失效。截取每1024 个连续的振动加速度数据点作为一个样本，最终采集到这两个空间滚动轴承全寿命期的总样本个数均为744 个。

表1 实验工况表Tab.1 Detailed working conditions

图3 空间滚动轴承振动监测平台Fig.3 Vibration monitoring platform for space rolling bearings

实验中被标记为工况C3 的实验数据来自Cincinnati 大学的滚动轴承加速寿命试验数据［9］。如图4 所示，将四个型号为ZA-2115 双列滚子轴承安装在轴承试验台的旋转轴上，使用转速为2000 r/min 的电机通过皮带驱动转轴，并通过弹簧机构在转轴和轴承上施加2721.55 kg（6000 lbs）的径向载荷，采样频率为20 kHz，每10 min 采集一次轴承的振动加速度数据。对每次采集的加速度数据截取前1024 个连续点作为一个样本，共获得全寿命期984个样本。

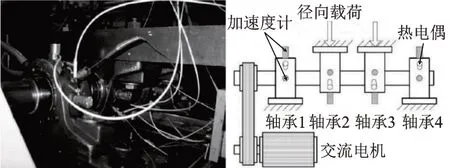
图4 Cincinnati 大学滚动轴承加速寿命退化实验台Fig.4 Accelerated rolling bearings life cycle degradation test platform in University of Cincinnati

在寿命阶段识别实验开始前需要对三个工况下的全寿命数据进行寿命阶段划分。首先对每个样本提取来自时域、频域和时频域的27 个特征［10］，然后用等度量映射（Isometric Mapping，Isomap）［11］方法对提取的特征进行维数约简，获得一维的主特征，接着用威布尔分布模型［12］对一维主特征构建可靠度评估曲线，得到三个工况下的（空间）滚动轴承的可靠度评估曲线分别如图5～7 所示。由于真空泵空间狭小，且两个空间轴承在真空泵内同时试验，导致空间轴承运行时的振动特征受到强烈的环境噪声干扰；同时，空间轴承所受轴向载荷随着轴承磨损和轴承间隙的改变而持续变化；且电机转速是非闭环控制，因而空间滚动轴承的转速具有一定波动性。以上原因造成空间滚动轴承的时域、频域和时频域振动特征的能量分布变得更为分散，进而Isomap 对以上振动特征的维数约简结果也随之变得更为分散，导致图5 和6 所示空间滚动轴承的可靠性评估曲线较图7 所示的普通滚动轴承波动更大。根据可靠度评估曲线，将全寿命数据划分为正常阶段、早期退化阶段、中期退化阶段、完全失效阶段这4 个阶段：从空间滚动轴承运行安全性、稳妥性考虑，将第一次出现可靠度0.9 对应的时间点作为划分正常阶段和早期退化阶段的时间点，该点也被视为空间滚动轴承精度失效阈值点［13］；将第一次出现可靠度0.5 对应的时间点作为划分早期退化阶段和中期退化阶段的分界点［14］；将第一次出现可靠度0.1 对应的时间点作为划分中期退化阶段和完全失效阶段的分界点［14］。

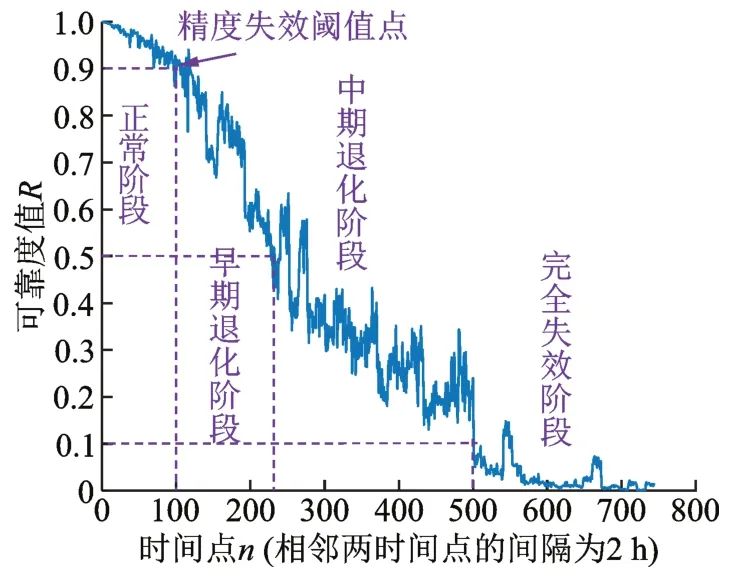
图5 空间滚动轴承1 的可靠度评估曲线Fig.5 Reliability assessment curve of space rolling bearing 1

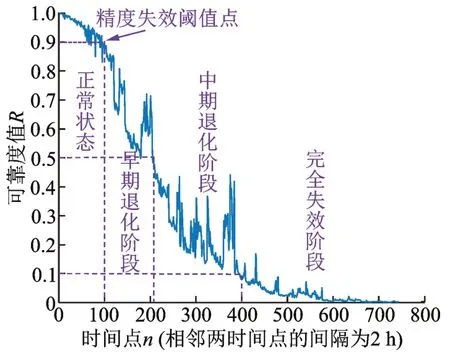
图6 空间滚动轴承2 的可靠度评估曲线Fig.6 Reliability assessment curve of space rolling bearing 2

图7 来自Cincinnati 大学的第二组实验中1 号滚动轴承的可靠度评估曲线Fig.7 Reliability assessment curve of rolling bearing 1 in the second set of experiments from University of Cincinnati

3.2 MAMTL 网络结构设计和参数设置

MAMTL 的网络结构设计如下：内环平行网络和外环元学习网络的特征映射函数都采用五层的卷积神经网络，该网络的具体配置如表2 所示；分布差异度量函数采用联合分布适配函数［15］；原型网络中的相似度函数采用如下的余弦相似度：

式中a，b表示向量。

MAMTL 的参数设置如下：内环平行网络参数的学习率α=4×10-2；外环元学习网络参数的学习率β=2×10-4；外环元学习网络的平衡约束参数γ=0.5；每一次训练内环平行网络的任务数N=8；每个任务中支持集样本和查询集样本的数量分别为K（每个任务包含两个阶段：第一阶段是求出支持集高维特征的损失函数并更新一次内环平行网络的参数；第二阶段是求出查询集高维特征的损失函数）。MAMTL 的网络结构和参数设置好后，在以下所有实验中均维持不变。

3.3 实验1 和分析对比

在本实验中，将工况C2 下的正常状态阶段、早期退化阶段、中期退化阶段以及完全止动失效阶段的样本（即全寿命样本）作为源域样本来识别工况C1 下的全寿命样本（即目标域样本）的寿命阶段（即：C2→C1）。实验前，分别对空间轴承2 和空间轴承1 的每一寿命阶段各随机取80 个样本作为用于实验的源域各寿命阶段的总样本和目标域各寿命阶段的总样本，即用于实验的源域总样本数和目标域总样本数分别为320 个。

（1）在源域按照1∶1∶1∶1 的比例为每一寿命阶段随机取K/4 个样本作为源域有类标签训练样本（即源域所有寿命阶段样本的总数为K，K≤320），在目标域中也按每一寿命阶段1∶1∶1∶1 的比例随机取样作为目标域待测样本，待测样本总数也为K。将每一个样本按其元素的先后顺序分段重组为相应的32×32 的矩阵作为MAMTL 的一个输入样本，然后依据第2 节所示的空间滚动轴承寿命阶段识别实现流程来用所提出的基于MAMTL 的寿命阶段识别方法进行（工况C1 下）空间滚动轴承1 的寿命阶段识别。这里将本文所提出的方法对当前目标域待测样本的四种寿命阶段识别准确率及平均识别准确率与其他三种迁移学习方法，即：联合分布适配（JDA）［15］、深度领域自适应（DDC）［16］、和改进迁移联合匹配（ETJM）［17］进行了比较。为了降低随机性带来的误差，每种方法取20 次实验结果的平均值作为其最后实验结果（下同）。随着源域有类标签训练样本总数的减少，寿命阶段平均识别准确率对比结果如图8 所示。在源域有类标签样本总数K=16时，所提出的方法和三种被比较的方法的寿命阶段识别准确率如图9 所示。同时，为了可视化展示MAMTL 的迁移和分类性能的优越性，利用t-分布随机邻域嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）算法［18］将K=16 时MAMTL 和其他三种被对比方法提取到的高维特征降维到二维平面，并以散点图的形式呈现在图10～13 中。

图8 空间滚动轴承1 寿命阶段的平均识别准确率对比Fig.8 Comparison of the average identification accuracy of the life stages of space rolling bearing 1

图9 源域有类标签样本总数K=16 时寿命阶段识别准确率Fig.9 Life stage identification accuracy of space rolling bearing 1 when the total number of labeled samples in source domain is K=16

图10 MAMTL 输出的高维特征经t-SNE 降维后的散点图Fig.10 Scatter plot of high-dimensional features output by MAMTL after dimension reduction by t-SNE

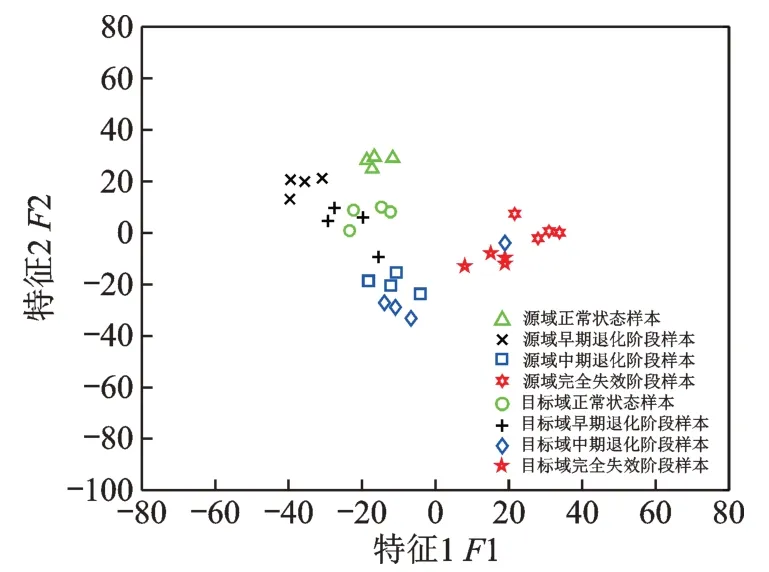
图11 DDC 输出的高维特征经t-SNE 降维后的散点图Fig.11 Scatter plot of high-dimensional features output by DDC after dimension reduction by t-SNE

图12 JDA 输出的高维特征经t-SNE 降维后的散点图Fig.12 Scatter plot of high-dimensional features output by JDA after dimension reduction by t-SNE

图13 ETJM 输出的高维特征经t-SNE 降维后的散点图Fig.13 Scatter plot of high-dimensional features output by ETJM after dimension reduction by t-SNE

由图8 和9 对比结果可知，随着源域有类标签样本总数的减小，四种方法虽然由于训练都不充分导致它们的寿命阶段识别准确率都逐渐下降，但所提出的基于MAMTL 的寿命阶段识别方法始终能得到比其他三种方法更高的寿命阶段识别精度。由图10～13 的对比结果可知，所提出的MAMTL 相比其他三种迁移学习方法能使得源域和目标域中相同类别的样本更好地聚合在一起，且两域中不同类别的样本之间也相对更为分散，因此MAMTL 的迁移和分类性能更好，基于MAMTL 的寿命阶段识别方法的识别精度也就更高。

（2）在源域中按照1∶1∶2∶4 的比例取正常阶段和早期退化阶段的样本数分别为K/8，取中期退化阶段样本数为2K/8，取完全失效阶段样本数为4K/8用作源域有标签样本（即源域所有寿命阶段样本的总数为K，K≤160），在目标域中也按每一寿命阶段1∶1∶2∶4 的比例随机取样作为目标域待测样本，待测样本总数也为K。将本文所提出的方法对当前目标域待测样本的四种寿命阶段识别准确率及平均识别准确率与其他三种迁移学习方法进行了比较。随着源域有类标签训练样本总数的减少，寿命阶段平均识别准确率对比结果如图14 所示；在源域有类标签样本总数K=24 时，所提出的方法和三种被比较的方法的寿命阶段识别准确率如图15 所示。

图14 空间滚动轴承1 寿命阶段的平均识别准确率对比Fig.14 Comparison of the average identification accuracy of the life stages of space rolling bearing 1

图15 源域有类标签样本总数K=24 寿命阶段识别准确率Fig.15 Life stage identification accuracy of space rolling bearing 1 when the total number of labeled samples in source domain is K=24

由图14 和15 的对比结果可知，随着源域有类标签样本总数的减小以及源域不同类标签样本数变得不均等，四种方法由于训练都不充分、不均衡导致它们对四种寿命阶段的识别准确率及平均识别准确率都逐渐下降，但所提出的基于MAMTL 的寿命阶段识别方法的识别准确率及平均识别准确率分别还是比其他三种方法更高。

3.4 实验2 和分析对比

在本实验中，将工况C3 下的正常状态阶段、早期退化阶段、中期退化阶段以及完全止动失效阶段的样本（即全寿命样本）作为源域样本来识别工况C1 下的全寿命样本（即目标域样本）的寿命阶段（即：C3→C1）。实验之前，分别对工况C3 下的1 号滚动轴承和工况C1 下的空间轴承1 的每一寿命阶段各随机取80 个样本作为用于实验的源域各寿命阶段的总样本和目标域各寿命阶段的总样本，即用于实验的源域总样本数和目标域总样本数分别为320 个。

在源域中按照4∶3∶2∶1 的比例取正常阶段的样本数为4K/10，取早期退化阶段的样本数为3K/10，取中期退化阶段的样本数为2K/10，取完全失效阶段的样本数为K/10 用作源域有类标签样本（即源域所有寿命阶段样本的总数为K，K≤200），在目标域中按照每一寿命阶段2∶4∶1∶3 的比例进行随机取样作为目标域当前待测样本，待测样本总数也为K。将本文所提出的方法对目标域待测样本的四种寿命阶段识别准确率及平均识别准确率与其他三种迁移学习方法进行了比较。随着源域有类标签训练样本总数的减少，寿命阶段平均识别准确率对比结果如图16 所示。在源域有类标签样本总数K=30 时，所提出的方法和三种被比较的方法的寿命阶段识别准确率如图17 所示。

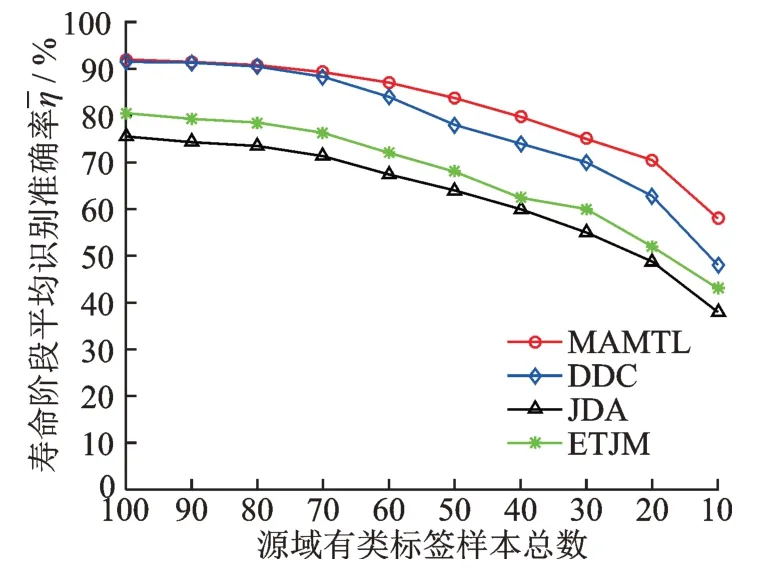
图16 空间滚动轴承1 寿命阶段的平均识别准确率对比Fig.16 Comparison of the average identification accuracy of the life stages of space rolling bearing 1

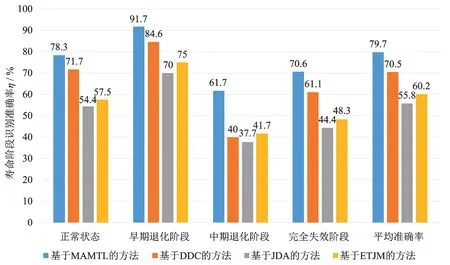
图17 源域有类标签样本总数K=30 寿命阶段识别准确率Fig.17 Life stage identification accuracy of space rolling bearing 1 when the total number of labeled samples in source domain is K=30

图16 和17 的对比结果表明，即使源域有类标签样本总数逐渐减小以及源域不同类标签样本数变得不均等，所提出的方法对四种寿命阶段的识别准确率及平均识别准确率也分别比其他三种被对比方法更高。

4 结论

（1）在所提出的MAMTL 中，将模型无关元学习和迁移学习相结合以实现多任务同步平行训练从而代替传统的迭代训练，以改善MAMTL 的泛化性能。具体而言，MAMTL 中的外环元学习网络每一次更新的参数都是由内环平行网络中多个任务的所有损失函数共同作用得到的全局最优解，所以以这个全局最优解作为外环元学习网络的起始点去学习新的任务时仅需要少量迭代次数就能使外环元学习网络达到收敛，即又好又快地适应新的迁移学习任务，因此MAMTL 具有良好泛化性和域适配性。

（2）在MAMTL 中构建了新型原型网络作为分类器，它将源域每一类别中所有的样本用一个原型表示，通过计算目标域待测样本与原型的相似度完成目标域待测样本的分类，这样避免了因源域不同类别样本数量的差异而造成对不同类别样本分类精度差别过大（即对少样本类别的样本的分类精度过低）问题；同时，在计算目标域待测样本与不同原型的相似度时没有参数学习的过程，所以在训练小样本情况下不会出现过拟合现象。此外，MAMTL的新型原型网络是与MAMTL 匹配的框架性模型无关原型网络，即该新型原型网络可以根据MAMTL 所采用的特征映射函数和分布差异度量函数来选择使分类精度最优的相似度函数，如余弦相似度、欧几里得距离、皮尔逊相关系数等。

（3）MAMTL 的以上优势使得它可利用空间滚动轴承历史工况下的少量、非均等寿命阶段样本（即有类标签训练样本）来对当前待测样本进行较高精度的寿命阶段识别。