桥梁断面范德波尔振子涡激气动力模型参数非线性化的能量原理

2023-11-20陈泓欣张志田曾加东

振动工程学报 2023年5期

陈泓欣，张志田，曾加东，郄凯

（1.海南大学土木建筑工程学院，海南海口 570228；2.湖南大学土木工程学院，湖南长沙 410082）

引言

涡振是一种兼有自激与限幅性质的周期性振动，是由钝体尾流中旋涡的交替脱落所致［1］，但根据钝体的不同形态其机理表现也不同［2］。涡振会使桥梁的正常使用受到严重影响，甚至引起构件的疲劳破坏［3］。因此准确分析大跨度桥梁的涡振响应有实际工程意义［4］。

对桥梁涡振特性的研究主要依赖节段模型风洞试验或计算流体力学（CFD）数值模拟。涡激振动可以由Navier-Stokes 方程结合边界条件得出，但求解N-S 方程是困难的。Scanlan［5］提出了由简谐力项、气动阻尼力项与气动刚度项组成的非线性半经验涡激力模型。该模型把气动阻尼项改为由两个气动力参数控制的类范德波尔振子［6］，从而克服了线性模型不能反映涡振物理特性（如自激性质与限幅性质等）的缺陷。之后，文献［7-8］研究表明，Scanlan 经验非线性模型中简谐力项与气动刚度项在大质量比结构中均可忽略。从而Scanlan 非线性经验模型可简化为范德波尔升力振子模型，模型参数通过稳定的振幅识别。ZHU 等［9］针对扁平箱梁提出了一种非线性涡激力模型，并与Scanlan 的经验非线性涡激力模型进行了比较。XU 等［10-11］提出了一种采用多项式表达的广义涡激力模型，通过比较评价了经验模型的优劣。这些模型也未能表达涡振时程中气动响应的非线性特征。文献［12］研究了阻尼非线性对涡激力模型参数的影响。GAO 等［13］尝试了一种能描述涡振与颤振的自激力的模型，分析了该模型气动力参数随折减风速的演变。CHEN 等［14］通过CFD 数值模拟研究了扁平闭口箱梁涡激力的演变历程。ZHANG 等［15］通过SIDF模型研究了涡激气动特性随瞬态振幅的分布。ZHANG 等［16］将气动力参数简化为一个，给出了基于瞬态和稳态振幅的识别结果，并用于不同阻尼比下的涡振振幅预测。在气动特征的应用上，张志田等［17］基于能量原理得到节段模型至全桥模型的幅值换算关系。许坤等［18］通过两自由度尾流振子模型研究了桥梁节段至全桥的涡振幅值换算关系。周奇等［19］、秦浩等［20］也研究了涡振幅值换算关系。这些换算关系未考虑非线性气动特性随瞬态振幅的影响。

通常，范德波尔振子涡激力模型是常参数模型。常参数模型能正确描述某一风速、某个确定的结构阻尼比下模型的涡振稳态振幅，但不能描述涡激气动力性能随振幅演变的非线性特性。这种情况下识别出来的模型应用十分有限，比如结构阻尼比变化后模型即失效。而对阻尼比的依赖与高度敏感性是涡激共振的特征之一。针对这一问题，本文通过能量原理，探索涡激气动力模型参数非线性化的基本方法。

1 涡激气动力模型

1.1 常参数范德波尔振子模型

以文献［7-8］提出的经验非线性模型为基础，进行简化后可得到如下双参数范德波尔振子涡激气动力模型：

式中ρ为空气密度；D为节段模型特征高度；U为平均来流风速；Y1为试验识别得到的参数，为折算频率K=Dω/U的函数，其中ω为结构振动圆频率；y和分别为结构位移和速度；ε为试验识别的气动力参数；L为节段模型长度。

式（1）具有自激与限幅的双重性质，其初始气动阻尼由Y1(K)确定，当其大于结构阻尼时开始形成涡激振动，此时具有自激性质；随着振幅的增大，参数ε发挥并扩大正阻尼作用，从而可限制振幅的无限发展，并最终形成极限环。式（1）表达的气动力在宏观上表现为阻尼形式，它不能反映气动力对结构振动频率的影响，但通常情况下，涡激共振时结构的频率变化可忽略不计。从能量吸收或耗散的角度来看，识别出参数ε随风速以及振幅的演变特性后，该模型就具有了完备性。即可真实地反映各风速下结构的初始气动阻尼及其随振幅的演变，从而可重现结构的涡激振动响应。

1.2 参数非线性化及识别原理

对于节段模型，其运动方程可表示为：

式中m为模型的振动质量；c为结构阻尼系数；k为悬挂系统的等效刚度；y和分别为模型的位移、速度和加速度。

在一个周期T内，气动力所做的功Wa为：

结构振幅变化时，位移以及速度时程可分别表示为：

式中yT为模型在周期T内的初始振幅；t为时间；λ为振幅增长或衰减指数。

结合式（1），（3）～（5）可得：

引入指数λ与振动宏观阻尼比ξ的关系：

则式（7）可重新写为：

通常情况下，即使是明显的涡激共振，其宏观阻尼比|ξ|≤0.05，此时有：

β相对α的误差随阻尼比ξ的变化曲线如图1 所示。从图中可知，在阻尼比绝对值小于5%的情况下，该误差小于1%。因此Wa可简化为：

图1 β 相对α 的误差随阻尼比ξ 的变化Fig.1 Variation of the β-to-α error with damping ratio ξ

结构阻尼力做功Wc为：

式中c为结构阻尼系数，代入时程函数得：

式（11）和（13）分别表示气动力和阻尼力在单个周期内所做的功与结构振幅yT以及指数λ的关系。当模型振动为稳定的极限环时，气动阻尼与结构阻尼在一个周期内做功互相抵消；当模型处于振幅增长阶段时，单个周期内二者做功有一定差值，具体表现为系统的机械能增大，其增量ΔW为：

式中 ∆y为一个周期内的振幅增量，文献［21］研究表明高阶力分量对振动能量输入贡献甚微，因此可忽略∆y高阶项。

由能量守恒定律可得，气动阻尼力做功、结构阻尼力做功以及二者差值的关系为：

将式（11）和（13）代入式（15）后化简得：

从结构动力学可知，在单个周期内有：

令初始气动阻尼系数为：

则式（16）可写成：

根据上式可识别参数ε随振幅yT的演变关系。但前提是先识别出Y1，从而确定初始气动阻尼cin。

在稳定的极限环状态下，∆y=0，∆W=0，此时式（19）简化为：

上式表明稳态振动时ε的值由结构阻尼、初始气动阻尼以及稳态振幅三者共同确定。

要得到式（18）表示的初始气动阻尼，需要先根据以下公式识别出Y1：

式中n为所采用的运动周期数，可根据实际情况选用时程曲线开始的若干个周期；δn为与n相对应计算得到的对数衰减率：

式中yT0为参考时刻0 的结构振幅；yTn则为相对于时刻0 第n个周期后的振幅。

参数识别后，根据式（18）可得到初始气动阻尼比为：

2 应用算例

本文采用图2 所示的桥梁主梁断面制作了缩尺比为1∶50 的节段模型并进行了涡激共振风洞试验，试验装置如图3 所示。模型主要特性如表1 所示，试验雷诺数范围为1.0×104～1.3×104。传统涡激共振风洞试验中，通常在某一级风速下达到稳态振幅后再增加风速，连续测试其在下一级风速下的振动。与传统方法不同的是，在本文的试验过程中，每级风速下须首先控制模型至静止状态，再让其自由发展到等幅振动状态，从而得到各级风速下涡激振幅的完整演变过程。

表1 模型主要特性Tab.1 Major properties of the model

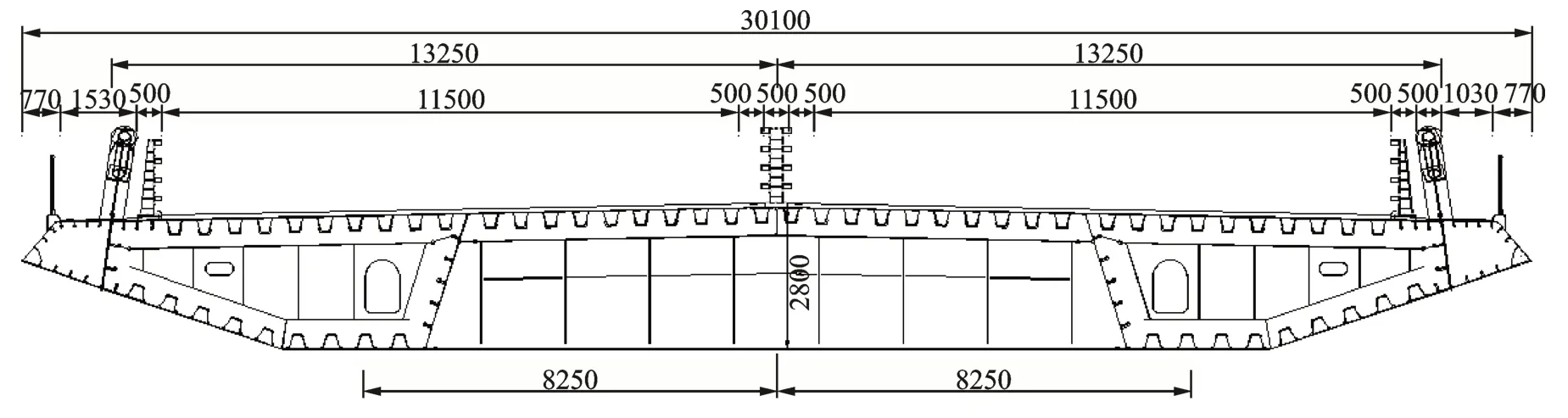
图2 桥梁主梁断面构造图（单位：mm）Fig.2 Configuration of the bridge girder section（Unit：mm）

图3 节段模型测振试验装置Fig.3 Experimental set-up of the sectional model vibration test

图4 给出了该模型在均匀流场下的涡振锁定区间。锁定区间内共测试了六组时程曲线，相应的振幅演变曲线通过Newmark-β法计算，结果如图5 所示，U/（fD）=10.19 时的时程局部细节如图6 所示。在识别初始气动阻尼参数时，取时程曲线起振时若干个周期进行分析，如图7 所示。但受小振幅以及特征紊流随机激励的影响，具体取几个周期进行分析是一个比较难以确定的问题，因此初始气动力参数的识别结果受多种因素制约。在图7 中，根据气动阻尼比将给定时程划分为初始气动阻尼识别区、参数演变区和稳定区。其中，初始气动阻尼识别区以表观阻尼比是否接近常值确定；参数演变区内气动阻尼比依赖结构振幅，呈现明显的非线性特性；稳定区结构振幅也不再增加。

图4 涡振响应-风速曲线Fig.4 Vortex-induced resonance responses versus wind velocities

图6 涡振位移时程局部细节图Fig.6 Detailed view of time history of displacement of vortex-induced vibration

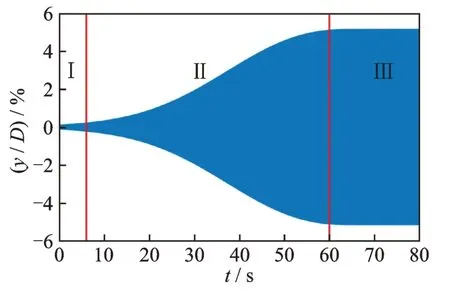
图7 参数演变分区（Ⅰ.初始气动阻尼识别区；Ⅱ.参数演变区；Ⅲ.稳定区）Fig.7 Parameter evolution zones（Ⅰ.The initial aerodynamic damping identification zone；Ⅱ.The parameter evolution zone；Ⅲ.The stable zone）

本文采用模型的涡激共振基本信息及所识别的初始气动阻尼参数如表2 所示。尽管锁定区间内涡激振幅值有较大的变化，但初始气动阻尼比ξin却基本保持一恒定值。

在每一级风速下，初始气动力参数Y1(K)确定后，保持其数值不变，根据式（19）可得另一参数ε随振幅的非线性演变特征，如图8 所示。由式（1）可知，正值的参数ε代表等效的正阻尼特性。图8 的演变曲线则表明随着结构振幅的增加，参数ε的值在不断减小。ε随着振幅增加而减小的现象容易形成一种假象，即阻碍结构振幅恶性演化的效应在不断降低。但实际上，模型很快就达到了稳定的极限环状态。

造成这一假象的主要原因是ε的数值并不能与该项气动力效应做的功直接联系起来。为更好地探索参数ε的限幅性质，考察由该项引起的非线性气动阻尼比ξε。令Wε为限幅参数项气动阻尼力做的功，容易得出其表达式为：

Wε所形成的等效非线性气动阻尼系数cε可按下式计算：

将式（24）代入得：

根据式（26）进而可得非线性气动阻尼比ξε为：

式（27）给出了ε对气动阻尼的贡献，由式（27）可知ξε由初始气动阻尼参数Y1与振幅yT控制。基于式（27）可识别出ξε的演变结果，如图9 所示。对比图8 与9 可知，尽管参数ε随振幅增长而降低，但非线性气动阻尼比ξε仍然随着振幅的增加而增加，且增长的规律是非线性的。在振幅演变最终极限环阶段，式（27）所示的阻尼比与初始气动阻尼比以及结构阻尼比三者之和为零，即

图9 涡振锁定区间内 ξε 的演变Fig.9 Evolution of ξε within the vortex-induced resonance lock-in range

式中ξs=为结构阻尼比；ξin=为初始气动阻尼比。初始气动阻尼比为负可提供结构振动所需能量，克服结构阻尼后使结构产生振幅递增的振动；非线性气动阻尼比提供正气动阻尼使结构振动达到限幅作用。

对于给定气动外形的桥梁断面，其初始气动阻尼比只是风速的函数，即ξin=ξin(Ur)；而ξε则为风速与振幅的函数，即ξε=ξε(Ur，yT)。从图9 可知，稳定的涡激共振极限环对应着ξε=-ξs-ξin的状态。因此通过试验识别出ξε(Ur，yT)后，对于更大的结构阻尼比的情况（即>ξs），由于--ξin<-ξs-ξin，因此=--ξin<ξε，即ξ'ε出现在图9中原来的路径上，其最终振幅可直接根据图中的函数关系找出。对于更小的结构阻尼比，由于>ξε出现在图中最高点的上方，因此无法预测其最终振幅。

值得指出的是，本文采用的范德波尔振子涡激力模型只考虑了自激气动力而忽略了强迫力。由于强迫力与自激力是不同性质的气动力，因此模型识别得到的初始气动阻尼是基于能量平衡的、具有某种“等效”性质的气动阻尼，由其带来的影响值得进一步研究。