基于全流量光学传感器的磨粒运动特性研究*
2023-11-20刘珍珍左洪福
刘珍珍,刘 岩,左洪福,王 涵,费 航
(南京航空航天大学民航学院民航飞机健康监测与智能维护重点实验室,江苏 南京 211100)
0 引 言
国外研究表明,由摩擦导致的磨损是材料和机械设备失效的主要原因[1],所以滑油携带了表征设备健康状态的多维信息,如铁、铜、陶瓷等,其特征能够反映磨损的模式、机理以及严重程度[2],故对油液进行状态监测就显得极其重要。传统的离线传感器有一定的滞后性,时效性差,正逐渐被市场所淘汰。基于在线监测传感器近几年得到了快速发展,因为磨损颗粒的密度、直径不同,所以会呈现不同的电磁[3]、静电[4]、电容[5]等特性。从运动角度考虑,不同属性颗粒在油液中运动时会呈现不同的运动特性,故掌握磨粒在滑油中的运动规律,能够从运动学角度去在线识别磨粒,推动滑油磨粒监测技术的发展,有效预防早期故障的发生。
液固两相流的运动学研究在化工、水利[6]、海洋、矿物输送领域已有广泛应用。如重庆工商大学陈彬等人[7]对连续相(油液)建立了连续介质方程,分析了油样中低含量(小于0.1%)的铜颗粒与连续流体运动黏度的内在关系。颜欢[8]通过仿真模拟得到颗粒污染物在水平方管流场中的运动状态影响流场的湍流情况。Visitskii Y V 等人[9]通过数值分析研究了实心球形颗粒在重力、振动和Basset力的作用下,在静止粘性流体中的沉降运动。李琼[10]通过数值模拟在Fluent 中研究了同种属性不同直径的铁质颗粒经过回油管射流后在500 mm×200 mm×300 mm的液压油箱中的运动情况,发现粒径越小的颗粒跟随流体运动的性能越好,但因油箱尺寸较大,流体处于湍流运动状态,与管路中流体的层流运动(由管道雷诺数所决定)存在着本质性的不同,并且未进行验证实验。Khatibi M 等人[11]通过粒子图像测速仪(particle image velocimetry,PIV)和粒子追踪测速(particle tracking velocimetry,PTV)技术进行了不同直径的颗粒在矩形水流通道中运动的实验,并运用计算流体动力学(computational fluid dynamics,CFD)数值模拟对实验误差进行验证,但水和滑油存在本质性的不同,并且论文只研究了两种不同直径同种属性的颗粒在水流中的沉降运动。综上可得,目前关于润滑管路中不同种类磨损颗粒运动特性的固液两相流研究鲜见报道。
本文利用在线光学传感器从液固两相流运动学角度去分析航空发动机滑油系统管路中不同磨粒的动态特性,来考虑磨粒的识别问题。首先利用理论受力方程分析了磨粒运动的影响因素,再通过全流量光学传感器与目标跟踪算法进行了多组实验,结合多元回归分析方法,拟合得到磨粒运动的平均速度方程与各影响因素的重要性,最后通过实验验证了速度方程的预测效果。
1 磨损颗粒受力分析
本文对整体模型做以下假设:1)油液为牛顿流体;2)不考虑温度对流体的影响,流体的密度和粘度不随温度变化而变化;3)油液中磨粒的尺寸为微米(μm)量级,体积分数非常小,因此磨粒之间并无碰撞;4)流体为不可压缩流体;5)磨损颗粒形状为大小均匀的球形。
对磨粒的受力分析如下,当颗粒沿x方向运动时,受力示意如图1所示。其中,颗粒所受到的曳力如下

图1 磨粒受力示意
式中Rep=ρfd|up-uf|/μ,重力Fg=πd3ρpgn/6,浮力Ff=πd3ρfgn/6。其中,d为颗粒粒径;ρf,ρp分别为流体和颗粒的密度,kg/m3;ur,up分别为流体的流速和颗粒的运动速度,m/s;μ,υ分别为流体的动力、运动粘性系数;CD为黏性阻力系数;gn为重力加速度;ω为颗粒的旋转角速度;t,τ均为时间。分析以上各作用力,由文献[12]可知,Basset力(FB)、压力梯度力(Fp)、附加质量力、Magnus 力(Fm)、Saffman(Fs)力均可以被忽略。所以曳力、重力、浮力是最主要的相间作用力,根据牛顿第二定律建立拉格朗日模型下磨粒在油液中的运动方程
可以得到,颗粒的运动速度与油液的速度、粘度、颗粒的密度、直径等有关,由于重力、浮力与曳力的作用方向不同,所以这里的速度代表矢量。
2 实验系统
2.1 试验系统的搭建
实验在南京航空航天大学民航飞机健康监测与智能维护重点实验室中进行,整个系统包括管道动力系统、颗粒注入系统、磨粒观测系统3部分组成,图2为实验系统的简化示意。

图2 实验系统示意
如图2所示,在齿轮泵前方连接精度为20 μm 的过滤器;颗粒注入系统包括1 个细长的竖直开口(直径10 mm,高度50 mm,内部充满油液)和2 个可控制开关的球阀;磨粒观测系统包括全流量光学磨粒传感器与电脑,为了观测颗粒在稳定状态下的运动速度,所以在距离颗粒注入系统900 mm处放置全流量光学传感器,其3D图如图3 所示,主要包括光源、矩形光学观测芯片(外方内圆,避免光的折射作用影响磨损颗粒的拍摄)、镜头,相机等。系统管路全长3 m,横截面为圆形的油路管道内径为8 mm,其他主要的设备参数如下:油管:透明树脂管、内径8 mm/外径12 mm;齿轮泵:CBB2.5;相机:像元尺寸为3.45 μm、分辨率2 448 ×2 048;镜头:维视制造远心镜头;透射光:工业LED面光源;变频器:功率2.2 kW、输入电压为三相380 V;滤油器1、滤油器2:20 μm滤芯。
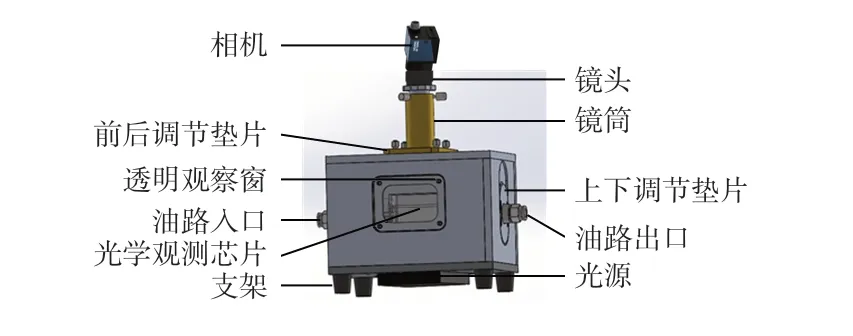
图3 全流量光学传感器3D图
具体方法为:实验开始后首先关闭颗粒注入系统的球阀1,打开球阀2,启动管道动力系统,利用齿轮泵从油箱中抽取抗磨液压油,目的是让油液到达球阀1的高度,待系统运行稳定后,关闭阀2,打开阀1,将磨损颗粒投入,然后关闭阀1,打开阀2,这样确保颗粒在没有外力干扰的情况下,自然流入主管路,然后在油流的作用下,向前运动,这样就不会产生有人为附加的较高初速度的影响。如果管路中有大量气泡出现,可以降低油液流速后,通过在颗粒注入系统中插入一个内径为2 mm的空心塑料管来排出管路中的气泡,避免影响颗粒的观测。
实验中变量的设置及各个影响因素的参数如表1 所示,其中,颗粒的种类分别采用铁和铝颗粒,粒径分别采用200 μm和500 μm,油液的种类采用0w-40油与20w-50油(w表示“winter”,其前面的数字越小,说明油液的低温流动性越好),油液的流速采用0.5,1 m/s,共进行8次实验。

表1 实验设置及各个影响因素的参数
2.2 基于ECO的磨损颗粒跟踪算法
2.2.1 相关滤波器
相关滤波器的原理示意如图4 所示,具体求解方法如下:如果选择的滤波器为h,输入的图像为f,可以对两者进行相似性计算得到互相关函数g

图4 基于相关滤波器的跟踪方法示意
g值越大,则f与h的相关性越高。当g值取最大值时,f即为即为跟踪目标的图像。为了提高运算速度,经快速傅里叶变换(FFT)可以得到
其中,(*)为共轭,式(5)可以简化为
对于得到的每一个样本图像fi都存在与之相对应的gi,即
H*的更新公式为
2.2.2 高效卷积操作
提取输入样本图像fi的D种特征,记作。如果这D种特征所对应的特征图有N种分辨率,且以d∈(0,D]标记其中的某一个特征,n∈(0,N]标记其分辨率,那么其特征函数记作[n]。在每一种特征d上,可以用函数Jd来整合不同分辨率的特征图
式中Jd{f d}(t)为一个建立在希尔伯特空间L2(T)上插值函数bd的累积,插值函数bd是三次样条插值核b(t)位移后的叠加
如果特征d上的滤波器为h,那么其相关性响应
对于样本fi上的所有D种特征有连续响应函数
由于D种特征对于样本图像中目标的贡献度各不相同,假设其中的C(C<D)个特征对图像的表达起到决定性的作用,定义一个维度为D×C的矩阵P,那么特征图Jd{f d}可以降维为
综上可得,ECO算法[13]适合本实验的使用环境,利用ECO跟踪算法得到的跟踪效果如图5所示。

图5 实验2 与实验3 拍摄到的磨损颗粒以及跟踪效果
2.3 实验结果分析
2.3.1 多元线性回归模型
建立模型的回归方程为
式中a0为截距,a1,a2,a3,a4为未知系数,x1,x2,x3,x4分别为颗粒密度(kg/m3)、颗粒的粒径(μm)、油液的粘度(kg/m·s)、油液的流速(m/s),y为颗粒的运动速度(m/s)。利用R2与均方根误差(RMSE)验证模型的拟合效果。其中
式中n为试验次数,yi为每一次实验的因变量的真实值,为每一次实验因变量的预测值,为所有因变量实测值的平均值。当R2值大于0.7,可以认为模型的准确性较高,当RMSE值越小,代表模型的拟合效果越好。由于每个自变量的取值范围有很大的不同,所以,首先需要对每一个自变量的数据进行归一化处理,如下式所示
式中i=1,…,4,ximin为xi数据的最小值,ximax为xi数据的最大值。对归一化后的数据建立回归方程,得到回归模型的参数如表2 所示。R2=0.996 69,RMSE =0.021 88,模型拟合效果较好。所以

表2 回归模型参数
2.3.2 线性回归模型的验证
在全流量磨损颗粒运动特性研究系统中做了4 组实验,用多元线性拟合模型得到的预测值与真实值进行比对,如图6所示,表明拟合模型拟合效果良好,验证成立。

图6 真实值与预测值验证效果
3 结束语
1)根据牛顿第二定律,建立颗粒的运动学方程,结果表明,颗粒的运动与油液的速度、油液粘度、颗粒的密度、颗粒的直径有关。
2)基于自制的全流量光学传感器,搭建颗粒运动监测实验系统,并将ECO目标跟踪算法引入到磨粒速度的跟踪测算中,结果表明:该算法具有良好的测速能力,鲁棒性强。
3)利用多元线性回归模型对实验数据进行拟合并验证拟合效果,得到各因素对颗粒运动速度影响的重要程度,油流的速度与颗粒的运动速度呈正相关,颗粒的密度、油液粘度、颗粒的直径与颗粒的运动速度呈负相关。最后对模型进行了实验验证,表明该模型预测效果良好。
