例谈动量守恒定律在常见考题中的应用
2023-11-20张勇
张 勇
(山东省枣庄市第三中学)
为帮助学生全面、熟练地掌握动量守恒定律,本文将结合实际问题,对动量守恒定律的应用加以总结.
1 碰撞问题
碰撞问题是可借助动量守恒定律解决的主要题型,碰撞问题的特点是作用力大、作用时间短,相互作用过程中动量守恒.
例1如图1-甲所示,A、B两物体固定在光滑地面上,并由弹簧连接.t=0时,释放B,t=t1时,释放A,此时B速度为v0.A、B的a-t图像如图1-乙所示.已知0~t1和t1~t3时间内,B的a-t图像与坐标轴所围面积分别为S1、S2,则( ).

图1
A.A、B质量mA、mB满足mA<mB
B.S1、S2满足S1<S2
C.t=t4时刻弹簧的压缩量最大
D.0~t5时间内,弹簧对A物体的冲量大小为mBv0

t=t1时,弹簧处于原长状态;t1~t2时间内,vB>vA,弹簧不断伸长,t=t2时,伸长量最大,A、B共同速度为v,此过程可以视为完全非弹性碰撞,则由动量守恒定律有mBv0=(mA+mB)v,解得,此时弹簧弹力最大,A、B的加速度aA、aB均达到最大.由图1-乙可知aA>aB,由F=ma知,mA<mB,选 项A 正 确;t2~t3时 间 内,vB<vA,弹簧伸长量减小,t=t3时刻,弹簧达到原长,此时A、B相当于发生弹性碰撞,由动量守恒定律及推论可知,a-t图像与坐标轴围成的面积表示速度的变化量Δv,有S1=v0,,结 合mA<mB,得S1>S2,选项B错误;t3~t4时间内,vB<vA,弹簧逐步压缩,t=t4时,压缩量达到最大,由动量守恒定律得v=,选项C 正确;由t1~t5时间内A物体的a-t图像与坐标轴所围面积上下对称,动量变化为零,故只需计算0~t1内弹簧对A物体的冲量,即I=ˉFt=mBv0,选项D 正确.故正确选项为A、C、D.

本题为类弹性碰撞和非弹性碰撞的融合问题,在类弹性碰撞过程中满足动量守恒和机械能守恒.本题中,t=t2时刻,可视为完全非弹性碰撞;t=t3时刻,相当于弹性碰撞;t=t4时刻,又相当于完全非弹性碰撞.在解题中要明确整个运动过程,结合动量守恒定律、能量守恒定律解答问题.
2 弹簧模型
在弹簧模型中,受弹簧特性的影响,连接在弹簧两端的物体运动参量均会发生改变,往往是一个增加、一个减小.但是对整个系统而言,其在运动过程中动量守恒,故可以借助动量守恒定律进行解题,从而简化对过程的分析,提高学生的解题效率.
例2如图2所示,可视为质点的物块A、B在光滑水平面上,A左侧连有轻质弹簧,并处于静止状态,B以初速度1.2v0向右运动,零时刻B与弹簧接触,t0时刻,A、B速度均为v0,其间A、B加速度均不断增大,且A、B加速度大小之比为定值.v-t图像如图3所示,其中t=0至t=t0时间内,物块A位移为0.36v0t0,求:
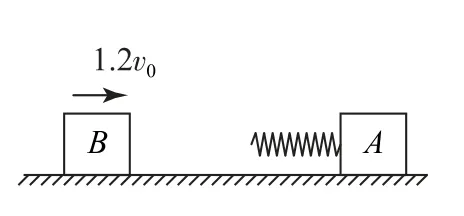
图2

图3
(1)A、B加速度大小之比;
(2)B对地的位移.

(1)t=0至t=t0时间内,由动量守恒定律有mB×1.2v0=(mA+mB)×v0,可得mB=5mA.A、B运动过程中,所受弹力大小相等、方向相反,则FA=mAaA,FB=mBaB,联立得aA∶aB=5∶1.
(2)B接触、压缩弹簧过程中,由动量守恒定律得
0~t0时间内,由位移定义可知
已知xA=0.36v0t0,联立解得xB=1.128v0t0.

A、B所构成的系统在整个运动过程中动量守恒,由此可确定两物块的质量关系,运用牛顿第二定律确定其加速度大小之比.在求B的位移中,结合动量守恒与位移定义,最终解答问题.
3 爆炸模型
爆炸过程中,系统内力远大于外力,系统动量守恒.因存在其他能量向动能的转化,故在爆炸后,系统的总动能会增加.在解题中,学生应围绕这些特点进行分析.
例3子弹在5 m 高处时,水平速度v0=2 m•s-1,此时弹体发生爆炸,分为甲、乙两部分水平飞出,并且m甲∶m乙=3∶1,忽略质量损失,g取10 m•s-2,则其轨迹可能为( ).
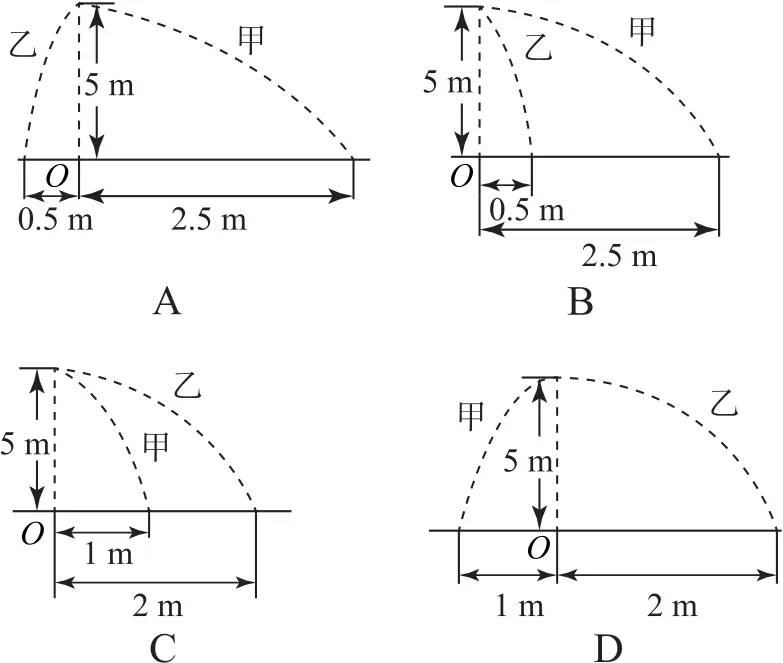


本题的爆炸情境较简单,仅涉及水平方向;在爆炸过程中,两部分受到大小相等、方向相反的力,在此基础上借助动量守恒定律进行解答.
4 验证实验
动量守恒定律的验证是高中阶段最为重要的实验之一,是高考考查的热点.相关实验及问题灵活多变,需要学生对动量守恒定律相关知识有准确的掌握,并能将其与平抛运动、能量守恒定律等诸多知识点进行结合应用.
例4如图4 所示,用“碰撞实验器”可以验证动量守恒定律.实验中,可以通过测量下面哪一物理量间接测定小球碰撞前后的速度大小( ).

图4
A.小球高度hB.小球抛点距地面高度H
C.小球落地时间 D.小球平抛运动射程

在本实验中,m1、m2碰撞发生在水平面,即小球离开“碰撞实验器”后做平抛运动,且落地时间相同.根据平抛运动的相关公式,可以得到,当已知小球平抛运动的射程时,便可以得到碰撞后m1、m2的速度大小之比,从而验证动量是否守恒.故选项D 正确.

本实验中,要想验证动量守恒定律,首先需要确定两小球的质量,同时还需要知道其瞬时速度,测量瞬时速度较为困难,但可以根据平抛运动的水平射程来表示平抛的初速度.
在上述诸多问题的解答中,均可应用动量守恒定律.而灵活运用动量守恒定律可以拓展解题思路,提高解题效率,促进学生从动量的角度深入思考问题.另外,在日常学习中,学生应重视对相关知识与方法的总结与归纳.
(完)
