Electromagnetic interference assessment of a train-network-pipeline coupling system based on a harmonic transmission model

Minwu Chen · Jinyu Zhao · Zongyou Liang · Xin Gong · Yu Cao

Abstract The harmonics and resonance of traction power supply systems (TPSSs) aggravate the electromagnetic interference (EMI)to adjacent metallic pipelines (MPs), which has aroused widespread concern.In this paper, an evaluation method on pipeline interference voltage under harmonic induction is presented.The results show that the Carson integral formula is more accurate in calculating the mutual impedance at higher frequencies.Then, an integrated train-network-pipeline model is established to estimate the influences of harmonic distortion and resonance on an MP.It is revealed that the higher the harmonic current distortion rate of the traction load, the larger the interference voltage on an MP.Particularly, the interference voltage is amplified up to 7 times when the TPSS resonates, which is worthy of attention.In addition, the parameters that affect the variation and sensitivity of the interference voltage are studied, namely, the pipeline coating material, locomotive position,and soil resistivity, indicating that soil resistivity and 3PE (3-layer polyethylene) anticorrosive coating are more sensitive to harmonic induction.Field test results show that the harmonic distortion can make the interference voltage more serious,and the protective measures are optimized.

Keywords Induced voltage · Inductive coupling · Conductive coupling · Harmonic resonance · Electromagnetic interference

1 Introduction

Over the years, research on the electromagnetic interference(EMI) of metallic pipelines (MPs) has focused mainly on the impact of overhead transmission lines in power systems.The research in this field can be categorized into the following three areas [1-3]:

(1) Research on the principle of EMI and on methods for evaluating the impacts of AC overhead transmission lines on MPs.For instance, the method for calculating the induced voltage in MPs adopts electromagnetic field theory in conjunction with circuit model analysis.To simplify this evaluation method, the International Council on Large Electric Systems (CIGRE) recommended the use of a distributed parameter calculation model [4].

(2) Research on pipeline corrosion arising from the EMI caused by AC overhead transmission lines.The characteristics and mechanisms of AC corrosion and the influences of AC waveforms and frequencies on pipeline corrosion have been studied [5, 6].

(3) Research on the standard limit for electromagnetic induction in MPs from AC overhead transmission lines.Many standards have formulated limits for personal safety and AC corrosion under different working conditions [7, 8].

Nevertheless, as a result of urbanization and railway development, oil and gas pipelines in urban areas often share the same rights of way with electrified railways, and thus,the EMI on pipelines caused by AC traction power supply systems (TPSSs) has also attracted widespread attention.Figure 1 shows different degrees of corrosion on pipelines near an electrified railway.

Fig.1 Different degrees of corrosion on an MP near an electrified railway

Fig.2 EMI on an MP paralleling an electrified railway

Unlike AC overhead power lines in power systems, a 25 kV AC TPSS is a high-voltage power supply system that uses rails and the ground as the path for the traction return current.As these rails and the earth are not perfectly insulated, the operation of electric locomotives can lead to the leakage of current from the former to the latter.In other words, as opposed to the steady-state AC interference of a power system caused by inductive coupling [9, 10], the interference due to a TPSS is the instantaneous AC interference arising from the interaction between inductive and conductive coupling.The EMI caused by a TPSS is shown in Fig.2.

At present, many scholars have done a lot of research on the EMI caused by electrified railways and accumulated some achievements.As Milesevic [11] compared the induced voltage calculated using EMTP-ATP software with the exposure limits and proposed countermeasures for reducing the induced voltage.Chen et al.[12] analyzed the effects of traction load current, pipeline length, and soil structure parameters based on CDEGS software.However, these works concentrated mainly on interference at the fundamental frequency (50/60 Hz).It is well known that the traction load of an electrified railway is an impact and nonlinear load, which can cause power quality issues such as harmonics and negative sequences that have attracted much attention [13-15].Harmonics have always been a concern, for a TPSS, electric locomotives are the main source of harmonics.Recently, with the widespread operation of AC-DC-AC locomotives, the harmonic spectrum in traction networks has widened.When the harmonic frequency generated by a locomotive matches the natural frequency of the traction network, the TPSS is excited, thereby generating parallel or series harmonic resonance.Harmonic resonance can result in arrester overvoltage problems, cause electrical equipment to overheat, and exacerbate the effects of EMI on communication systems [16].Identically, resonance will also cause more serious interference to adjacent pipelines, potentially endangering the safety of personnel or causing oil and gas leaks.But the existing relevant standards and literature scarcely consider the effects of harmonic resonance on MPs [17-19].It is necessary to further study the influences of different harmonic distortions and resonances in TPSSs on adjacent MPs.The main contributions of this paper are addressed as follows:

i.The calculation method of pipeline interference voltage under harmonic induction is derived, which is used to analyze the mechanism and characteristics of AC interference and verify the effectiveness of the evaluation model.

ii.An evaluation model is established that integrates a TPSS, a pipeline system and an electric locomotive and is used to investigate the influences of different harmonic distortion and resonance on the pipeline interference voltage.

iii.The parameters affecting interference voltage such as locomotive position, pipeline coating material and soil structure are investigated.The corresponding protective measures are put forward and the protective effect is analyzed.

The remainder of this paper is organized as follows:Sect.2 derives the interference voltage calculation method.The harmonic resonance mechanism of the TPSS is introduced in Sect.3.In Sect.4, a train-network-pipeline integration model is built, and the effects of harmonics and resonance on the EMI therein are studied.In Sect.5, the factors and protection measures affecting the interference voltage are investigated, and field tests are performed.Finally, the conclusions are drawn in Sect.6.

2 AC interference voltage calculation on a MP

The EMI effects of a 25 kV AC TPSS on buried MPs include inductive, capacitive and conductive components [10].Under normal operating conditions, the interference generated by capacitive coupling can be ignored on account of the shielding effect of the earth, therefore the EMI on a buried MP is caused mainly by inductive coupling (from contact wires, rails, etc.)and conductive coupling (stray current).The methods for calculating the components of the interference voltage are as follows.

2.1 Calculation of the inductive coupling voltage

The inductive coupling of the TPSS to the buried MP is produced mainly by the catenary and rails.An MP laid parallel to an AC electrified railway is subjected to the strongest known induction interference, so it is taken as the research object.Based on circuit theory, the calculation of the induced interference voltage involves two steps [20].

2.1.1 Determination of induced electromotive force

The induced electromotive force (EMF) is used to describe the degree of inductive coupling from interference sources(i.e., catenary and rails).The unit EMF at a given frequency can be formulated:

where˙Iirepresents the current of the catenary,Zmidenotes the per-unit length mutual impedance of the catenary conductor with the MP, andnis the number of conductors.

Equation (1) states that the EMF is determined by the mutual impedanceZmiand the load current˙Ii.Under the constant current, mutual impedance determines the degree of interference.The simplified Carson’s formula is commonly used in calculating the mutual impedance between two conductors [21].However, studies have indicated that it is only accurate for a certain frequency range.Carson integral formula can calculate the mutual impedance between two remote ground loops at higher frequencies[20].In this paper, the calculation results of the two formulas at different frequencies are respectively shown in Fig.3 compared with the CDEGS simulation results.It can be seen that with the increase in frequency, the error between the calculation results of Eq.(2) and the simulation results is increasing, while the calculation results of Eq.(3) are close to the simulation results.Therefore,Eq.(3) is more accurate in calculating the mutual impedance at higher frequencies.

whereμ0is the permeability in vacuum,Dgrepresents the equivalent depth,dis the distance between the conductor and pipeline,fdenotes the frequency,His the conductor height, andhprepresents the buried depth of the pipeline.

Fig.3 Comparison between different calculation methods of mutual impedance ( ρ=100 Ω ⋅m , d = 250 m, H = 6.3 m, hp = 1.5 m): a real part of Zmi ; b imaginary part of Zmi

2.1.2 Calculation of the maximum inductive voltage

To accurately analyze the effect of inductive coupling, the buried MP needs to be regarded as a distributed parameter circuit [3], as shown in Fig.4.

The transmission line equations of MP can be written by the equivalent circuit in Fig.4.

whereUind(x) represents the voltage to ground of the pipeline atx, is the current flowing through the pipeline,Zdenotes the unit length series impedance,Yis the unit length admittance of the pipeline to ground, andE(x) is the unit lengthinduced EMF.

The general solution ofUind(x) andI(x) are

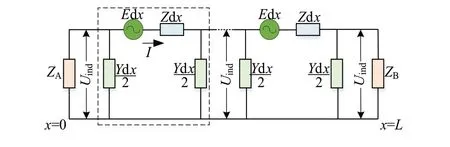
Fig.4 Equivalent circuit of the MP with the earth

where

γis the propagation constant of the earth return circuit in pipeline;Lrepresents the length of parallel pipeline;ZCdenotes the pipeline characteristic impedance;ZAandZBare the boundary impedances on both ends of the pipeline.

The buried pipeline self-impedanceZand ground admittanceYcan be calculated by Sunde formula, which can be used for the calculation of the pipeline parameters at different frequencies [3], expressed as follows:

whereεis permittivity of the soil, equal to 2.655 × 10-11F/m;εrindicates relative permittivity of the pipeline coating;ε0is permittivity of the air, equal to 8.85 × 10-12F/m;μ0denotes magnetic permeability of the air, equal to 4π × 10-7H/m;μris relative permeability of the pipeline, 300;ρpindicates resistivity of pipeline, equal to 9.78 × 10-8Ω·m;ρcdenotes resistance of anti-corrosion coating;δcis the thickness of the coating, ranging in 0.001-0.004 m;ais radius of the pipeline.

The direction and installation method of the MP and the electrified railway outside the parallel section determine the magnitudes of the boundary conditions (ZA,ZB) at both ends of the pipeline [22].Considering a typical pipe installation method in this study, the ends of the pipelines extend to infinity, and the parameters of the MP areZA=ZB=ZCandν1=ν2=0.Equation (5) can thus be expressed as

According to Eq.(16), the maximum induced voltage along the pipeline indicated in Eq.(17) arises at both ends(x=0,x=L):

Equations (16) and (17) indicate a V-shaped distribution of induced voltage on the pipeline.

For the current in the contact wires containing multiple frequencies, the total induced voltage is expressed as Eq.(18) after calculating the induced voltage at each frequency

whereUindhdenotes thehth harmonic-induced voltage and the value ofnis 100.

2.2 Calculation of the conductive coupling voltage

Figure 5 depicts how the conductive coupling interference caused by the TPSS on the parallel MP is calculated.

In Fig.5, taking traction load position as the coordinate origin, N (x,y) is any point on the parallel buried MP, andIgis the current flowing through the rail.Igis calculated by[12]

Fig.5 Calculation of the conductive interference voltage between railway and parallel buried pipeline

whereγprepresents the propagation coefficient of the rail-ground circuit, 1/m, andIis the traction load current in A.

The leakage current dIgflows into the earth through conductive coupling.An electric potential form at any point N(x,y) on the buried pipeline (as shown in Fig.6a), which can be calculated equivalently from the potential at point M (as shown in Fig.6b).Equation (20) gives the ground potential with the rail leakage current.

whereu=γx,ν=γy;Ω(u,ν) represents a special function;ρrepresents resistivity of soil layer in, Ω ⋅m.

By ignoring the reaction effect of the pipeline-ground on the rail-ground circuit and the mutual impedance between two circuits [12], N point to ground potential can be obtained from Eqs.(20) and (21).

whereλdenotes the shielding coefficient of the rail.

According to Eq.(21), the conductive coupling reaches a maximum at the traction load and gradually decreases to both sides.In addition, the pipeline parameters and parameters of the TPSS can affect the distribution characteristics of the induced voltageUN.Hence, when the traction currentIcontains harmonics, its characteristics need to be further analyzed.

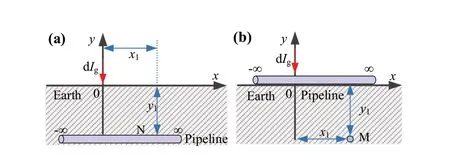
Fig.6 Principle of the conductive coupling calculation: a electric potential at point N on an MP; b electric potential at point M

3 Harmonic resonance mechanism of a TPSS

At present, AC-DC trains and AC-DC-AC trains are the two most widely used train types in electrified railways.The harmonic ratio of an AC-DC train is high because of the phase-controlled rectification, which contains mainly low frequencies.Given the development of power electronics technologies, the harmonic ratios of AC-DC-AC trains are small, but they have a wider harmonic spectrum.The traction network, namely, the channel used by electric locomotives to obtain electric energy, is an RLC distributed parameter system.When a locomotive is running, as viewed from the direction of the locomotive to the power supply system, the traction network and the traction substation can be regarded as a port network (the simplified equivalent circuit is shown in Fig.7).The TPSS experiences resonance when the highfrequency harmonic current frequency overlaps with the natural frequency of the traction network.This phenomenon can engender overvoltage and overcurrent conditions in the TPSS and worsen the effects of EMI.More details about the harmonic resonance mechanism can be found in [23-25].

4 Implementation and description of a train-network-pipeline integration model

4.1 Physical model

Considering an actual system, the spatial structure of a 25 kV single-phase AC TPSS and a parallel buried MP is shown in Fig.8.The TPSS is composed of a traction substation and traction network, where the latter includes conductors such as messenger wires, contact wires, steel rails, and return wires and the traction substation consists of a transformer and grounding grid.The power supply characteristics of the TPSS and the related characteristics of a traction substation are given in Tables 1 and 2, respectively.

Fig.7 Coupling model of a traction network and a train

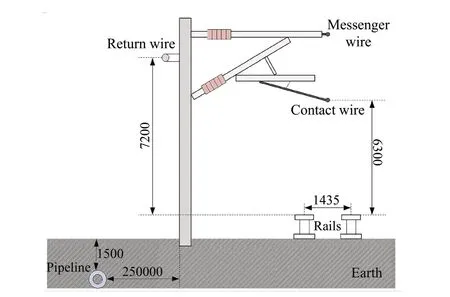
Fig.8 Spatial structure distribution of the direct power supply with return wires (single line) and a buried pipeline (unit: mm)

Table 1 Features of the direct power supply model with return lines

Table 2 Characteristics of the traction substation

4.2 Simulation model

CDEGS software is widely used in engineering grounding and electromagnetic field analysis and has become the recommended software for use in interference analyses with some national standards [26-28].The HIFREQ module can solve transient and steady-state problems in a frequency range from zero to several hundred MHz.For EMI, inductive and conductive couplings can be calculated simultaneously.Moreover, the FFTSES module is a fully integrated and automatic Fourier transform tool that can be used to calculate time-domain electromagnetic fields.

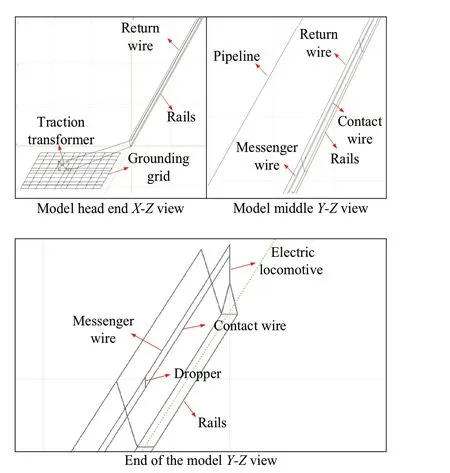
Fig.9 Integrated train-network-pipeline model

Based on the physical model shown in Fig.8, the trainnetwork-pipeline integrated model shown in Fig.9 is built in the HIFREQ module.This model is a true equivalent of an actual TPSS: the length of the AC traction system is 20 km,the coordinates in the 3D model are within the range of 0-20 km, and it is underlain by a parallel 5 km-long buried MP (8.5-13.5 km).The running rails are equivalent to conductors coated with a resistive coating.The parallel connection points of the return wires are 5 km apart.The electric locomotive located at 20 km.Note that the electric locomotive is the main harmonic source in the TPSS; Hence, the locomotive needs to be regarded as an ideal current source when studying the harmonic transmission of the TPSS.The specific analysis process is illustrated in Subsect.4.3.In addition, the simulation parameters of the pipelines, conductors, and rails are shown in Tables 3, 4, and 5.

4.3 Implementation of harmonic resonance

According to the above analysis, the electric locomotive is the main generator of harmonic resonance.To reflect the actual features, the traction load currentIL(t) can be defined fornharmonics:

whereωis the angular frequency andφnis the initial phase angle.

Then, to illustrate the EMI effects from harmonic distortion and resonance in the TPSS on an adjacentMP, simulations (executed in the FFTSES and HIFREQ modules) are performed in this section.Further details regarding the computation of harmonic distortion and the corresponding algorithms can be found in [19, 29].In this section, the main focus is the simulation of harmonic resonance.The explicit steps are as follows:

Table 3 Parameters of the MP in the simulation model

Table 4 Conductor parameters in the TPSS

Step 1 Perform Fourier decomposition on a pure 50 Hz traction load current signal with a 500 A amplitude to obtain frequencies in the FFTSES module.Then, use these frequencies to compute the electromagnetic field response in the HIFREQ module model.Notably, the HIFREQ model should be energized by the unit current signal.

Step 2 Compute the frequency-domain system responseU(ω) , thereby obtaining the maximum pipeline interference voltage at the different frequencies decomposed in Step 1, and then determine the resonant frequency range.

Fig.10 Electric potential on the buried pipeline

Step 3 Calculate the traction load harmonic current with the resonant frequency using Eq.(22).Then,perform frequency decomposition in the FFTSES module,and apply the resulting frequencies to compute the electromagnetic field response as in Step 1.

Step 4 Compute the time-domain system responseU(t).Then, obtain the time-varying induced voltage by applying an inverse Fourier transform to the frequencydomain interference voltage found in Step 3 in the FFTSES module.

4.4 Validation of the simulation model

4.4.1 EMI on the metallic pipeline

To verify the validity of the simulation model, the simulation results are compared with the theoretical calculation.Figure 10 shows the electric potential distribution on the buried pipeline produced by conductive coupling under the integrated train-network-pipeline model described in Subsects.4.1 and 4.2.The result shows that the electric potential decreases from the point of current flow (locomotive location) to both sides and reaches the maximum at the traction substation (TS).

Fig.11 Interference voltage: a interference voltage along the length of the pipeline; b maximum values of interference voltage at different frequencies

From Fig.11a, the total interference voltage is a “V”shape, which is the superposition of conductive and inductive coupling.In the following analysis, the main concern is the interference voltage at both ends and in the middle of the pipeline.The calculation results of the interference voltage at different frequencies and the simulation results are shown in Fig.11b, which shows that the error between the two is small and further illustrates the correctness of the simulation model.

Table 6 Resonance frequency in the TPSS at different locomotive positions

4.4.2 Harmonic transfer characteristics

It is necessary to first confirm that the determined resonance process is correct.There are two main aspects of the harmonic transmission characteristics in the TPSS researched in Refs.[30, 31]: (a) The resonance frequency does not change with the position of the traction load, but the magnification of the corresponding order of harmonics is different.(b) The resonant frequency decreases as the length of the catenary increases.

By changing the locomotive position to obtain the resonance frequency in the simulation model depicted in Subsect.4.2, Table 6 shows the regularity of the resonant frequency at TS changing with the position of the electric locomotive.The resonant frequency range is approximately 1650 Hz (33rd).The resonant frequency remains constant when the train position changes.However, the harmonic amplification varies among different positions.

Then, the length of the catenary is changed to obtain the resonance frequency when the locomotive position remains the same.Table 7 shows that the resonance frequency decreases as the length of the catenary increases.This is because the distributed capacitance of the traction network resonates with the reactance of the system.The longer the traction network length is, the larger the shunt capacitance and the lower the resonant frequency.

4.5 Case study

In this study, the harmonic current of the locomotive is divided into five cases to illustrate the effect of harmonic on the interference voltage.THDis an important parameter that reflects the degree of distortion of the actual waveform relative to the sine wave, which can be expressed as

wherehis the order of the harmonic,Ihis the root-meansquare of thehth harmonic current, andI1is the root-meansquare of the fundamental current.

According to Eqs.(22) and (23), the following train load current signals are defined.Each signal forms a corresponding simulation scenario, as shown in Table 8 (harmonic current content is derived from field test data and simulation value[32-36]).

Table 7 Resonance frequencies of different catenary lengths

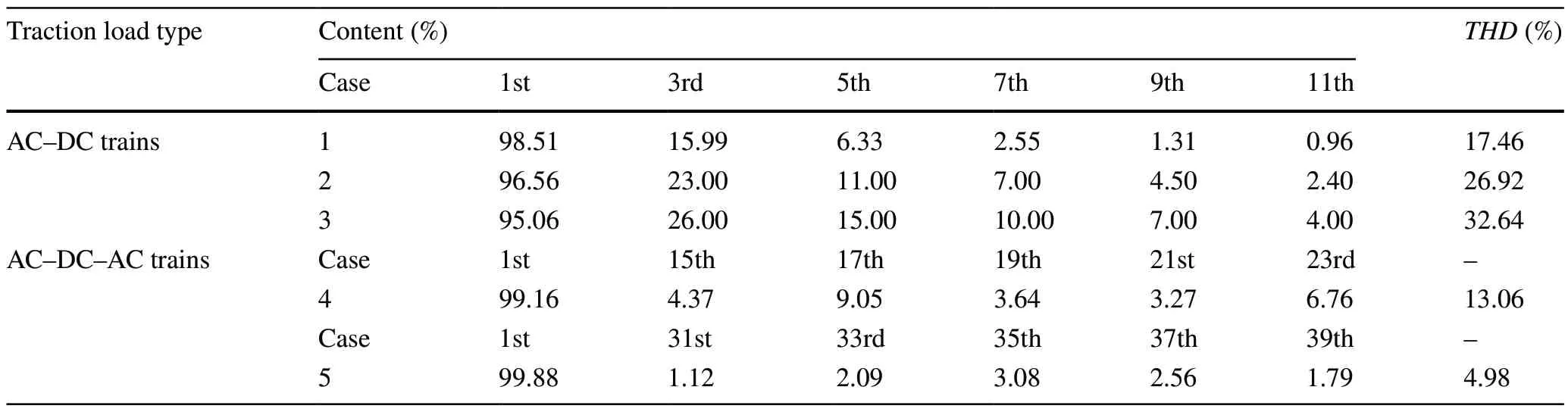
Table 8 Train load harmonic current (IL = 500 A)

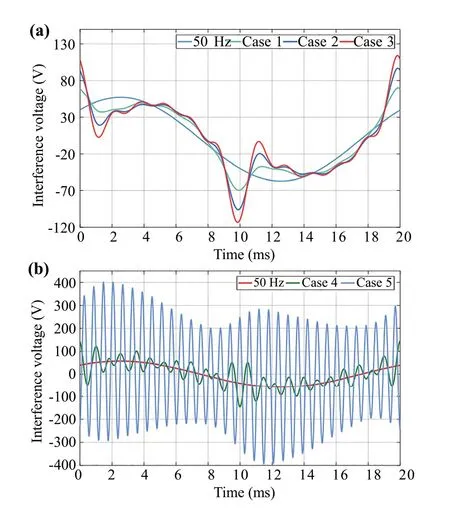
Fig.12 Time variation of interference voltage on the pipeline at 8.5 km: a AC-DC trains; b AC-DC-AC trains

The simulation approach of different train load currents follows the steps in Sect.4.3.

Figure 12 shows the time variation of induced voltage on the pipeline at 8.5 km under different cases.Figure 13 shows the time variation of induced voltage on the pipeline at 11 km(the middle of pipeline) under different cases.

Table 9 shows the amplitude variation of the interference voltage at different position of the pipeline in five cases, and the increase in the interference voltage relative to the fundamental under different cases is given.

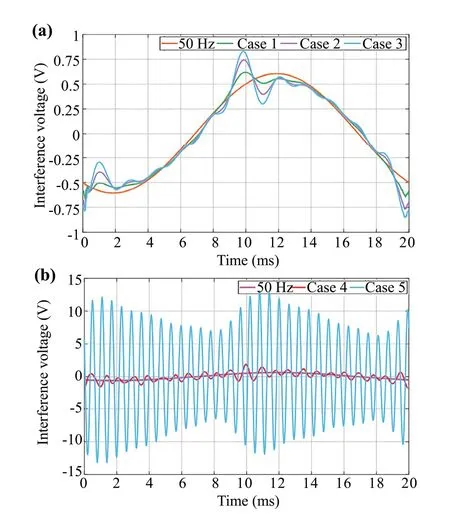
Fig.13 Time variation of interference voltage on the pipeline at 11 km: a AC-DC trains; b AC-DC-AC trains

From Fig.12a and Table 9, it can be observed that the interference voltage worsens when the influence of harmonic induction is considered.With the increase in harmonic distortion rate, the increase in interference voltage reaches 22.55%, 69.09%, and 99.28%, respectively.Comparing case 1 with case 4, we observed that the interference voltage in case 4 is more severe than the former.This is because the mutual impedance becomes an important factor affecting the interference voltage, which is positively correlated with the order of harmonics.In addition, as can be seen from Fig.12b, the order of harmonic currents in case 5 overlaps with the natural frequency of the TPSS generating a resonance phenomenon,resulting in amplification of the interference voltage.The interference voltage is amplified 7 times compared to the fundamental case.This not only causes a risk to personal safety, but also creates an impact on the pipeline and even causes it toleak.Furthermore, from the previous analysis, it can be seen that the interference voltage in the middle section of the pipeline is the lowest (Fig.13), but when the TPSS resonates, the interference voltage reaches 13.08 V, which should be given proper attention when designing the protection.

Table 9 Comparison of the interference voltage amplitudes

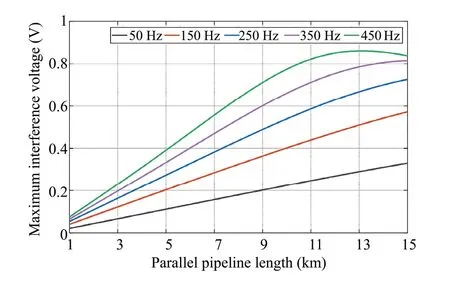
Fig.14 Effect of low order harmonics on the pipeline interference voltage

Finally, a crucial conclusion drawn from this work is that the EMI caused by the harmonics emitted by an AC TPSS on a parallel underground pipeline cannot be ignored.

5 Influence parameters and protection measures

In accordance with the analysis in Sect.2, the interference voltage on the pipeline is related to the EMF, parallel length of the MP, anti-corrosion layer material, and locomotive location.Therefore, the sensitivity and variation of interference voltage to these parameters under different harmonic orders are analyzed herein.

5.1 Effect of the MP parallel length

To comprehensively analyze the regular influence of the harmonic frequency on the pipeline interference voltage, load currents with the same amplitude (e.g., 1 A) but different frequencies are simulated.

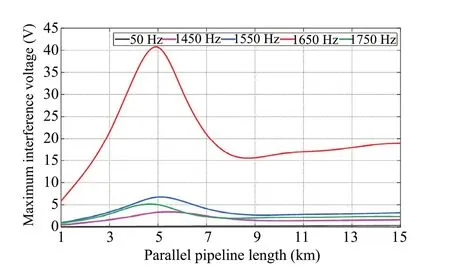
Fig.15 Effect of high order harmonic (including resonant frequency)on the pipeline interference voltage

Figure 14 shows that when the locomotive current contains low harmonics, as the frequency increases, the interference voltage rises.Moreover, when the frequency is less than or equal to 250 Hz, the interference voltage has a positive linear correlation with the parallel length.When the frequency is greater than 250 Hz, the interference voltage gradually flattens after the parallel length is greater than 13 km.

From Fig.15, when the locomotive current contains high harmonics, the closer the harmonic order is to the resonant frequency, the greater the interference voltage.In addition,the interference voltage first gradually increases with the length of the pipeline, reaches the maximum value when the pipeline length is 5 km, then decreases, and finally becomes stable.The reason for this phenomenon will be explained theoretically.The maximum induced voltage underhth harmonic is

whereEhis the unit induced EMF generated by thehth harmonic current, andγhrepresents the propagation constant of thehth harmonic.γhLdetermines the size of (1-e-γhL) ,andγhis a constant at the specified harmonic frequency,which means that the interference voltage increases with the pipeline length, finally reaching the maximum value.However,γhwill increase with the harmonic frequency [3],andLneeds to be reduced so that (1-e-γhL) reaches the maximum.Therefore, the higher the harmonic frequency,the shorter the parallel length of the pipeline with the maximum interference voltage.

5.2 Position of the locomotive

As the locomotive position changes, the conductive coupling also changes, which affects the interference voltage on the pipeline.This is because the TPSS uses the rail and the earth as the return current path, and the movement of traction load changes the proportion of current in rails and earth.In this study, the distribution of the maximum interference voltage and locomotive position is investigated when the distance between the locomotive and the traction substation varies within 2-20 km.

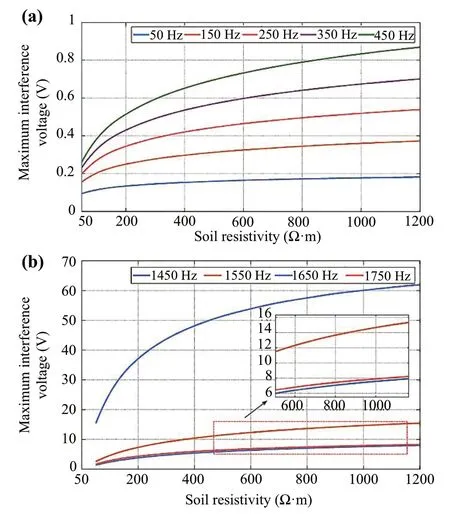
Fig.17 Interference voltage at different soil resistivities: a low order harmonic; b high order harmonics (including resonant frequency)

The interference voltages at different locomotive positions under a single harmonic are shown in Fig.16.In low order harmonics, the locomotive is located in the range of 2-8.5 km, and the pipeline interference voltage is mainly generated by conductive coupling.When the locomotive passes through the parallel area of the pipeline, the interference voltage increases gradually due to the joint effect of inductive coupling and conductive coupling.When the distance exceeds approximately 13.5 km, the inductive interference basically remains unchanged and plays a major role,so that the interference voltage tends to be stable.

5.3 Soil resistivity

As the soil resistivity is involved in both the mutual impedance and the propagation constant, it is difficult to reveal its effect on the interference voltage through an analytical evaluation.Therefore, based on the integrated simulation model, the distribution of interference voltages under the typical operating conditions (50-1200 Ω·m) is studied.

Table 10 Relevant parameters of anti-corrosion layer material

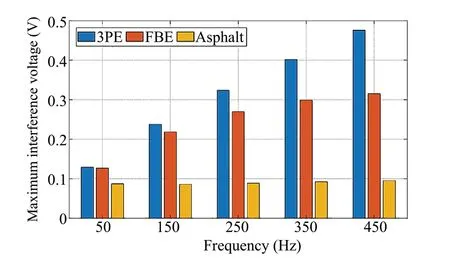
Fig.18 Effect of low order harmonics on the pipeline interference voltage

Fig.19 Effect of high order harmonics (including resonant frequency) on the pipeline interference voltage

Figure 17 shows the relationships between the soil resistivity and interference voltage at different frequencies.Firstly, both the lower harmonics and the higher harmonics it can be found that the interference voltage first increases with the increase in soil resistivity, and then gradually becomes flat.Otherwise, in low order harmonics, interference voltage increases with the increase in harmonic frequency.It can be concluded that soil resistivity is sensitive to harmonic induction interference.The influence of soil resistivity should be fully considered in pipeline interference assessment, and relevant tests should be carried out in the field environment.

5.4 Anti-corrosion layer material

Commonly used anticorrosive coating materials are 3-layer polyethylene (3PE), fusion bonded epoxy (FBE), and asphalt.The coating resistance mainly influences the real part of the pipeline self-admittance.In this paper, the influence of coating materials on the interference voltage is analyzed.The coating parameters are shown in Table 10.

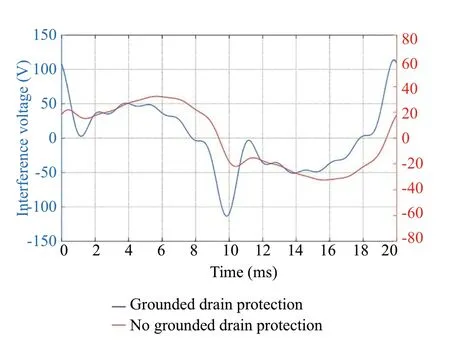
Fig.20 Time variation of interference voltage at 8.5 km in case 3

Fig.21 Time variation of interference voltage at 8.5 km in case 5

Figure 18 shows the induced voltage of the pipeline under different coating materials.It can be seen that the higher the coating resistance, the higher the induced voltage.What’s more, the increase in interference voltage at 450 Hz relative to the fundamental is 233.4%, 117.4% and 6.4%, respectively.It can be derived that the interference voltage on the pipeline-coated asphalt is insensitive to harmonics.The interference voltage on the pipeline-coated 3PE is very sensitive to harmonics.Therefore, the choice of coating materials needs to be considered in assessing harmonic interference to pipelines and in making protective designs.

Figure 19 shows the interference voltage of the pipeline under high order harmonics.It can be found that the resonant frequency intensifies the interference voltage, in especial the voltage of pipeline coated with 3PE material is more serious.

Fig.22 Influence of copper belt length on protection effect

Fig.23 Schematic diagram of pipeline interference test along a railway

Fig.24 Interference voltage at KP1 with different harmonic distortion rates

5.5 Protection measures

In the actual project, various protection measures are generally used for underground buried metal pipelines, such as sacrificial anode method and grounded drain protection.The grounded drain protection is simple, economical and widely used in practical engineering.In this study, taking grounding drain protection as the research object, the protective effect is analyzed.A 200 m long copper belt is laid along both ends of the pipeline.The copper belt with a radius of 0.01 m is connected to the pipeline.The relative resistivity of the copper wire is 9.86, the relative permeability is 300, the buried depth is 1.8 m, and the bare copper strip is 0.5 m away from the pipeline.

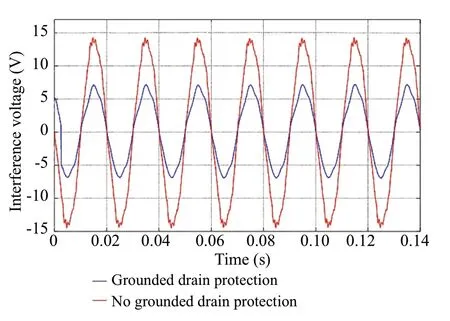
Fig.25 Time variation of interference voltage at measuring point KP1

Fig.26 Time variation of interference voltage at measuring point KP2

Figure 20 shows the interference voltage variation after grounding drain protection is applied in case 3.The interference voltage decreased by 71.4% from 113.3 to 32.4 V.

Figure 21 shows the interference voltage variation after grounding drain protection is applied in case 5.The interference voltage is reduced from 401.6 to 51.47 V, a decrease of 87.18%.In summary, for the effect of harmonic distortion and resonance, grounded drain protection can still effectively reduce the interference voltage.

Figure 22 shows the influence of the length of the copper bar on the protective effect in case 3.It can be seen that the length of the parallel copper bar is not the longer the better.When the length of the copper bar exceeds 300 m, the protective effect gain caused by increasing the length of the copper bar is not obvious.Therefore, the length of copper bar can be appropriately selected in the engineering design.

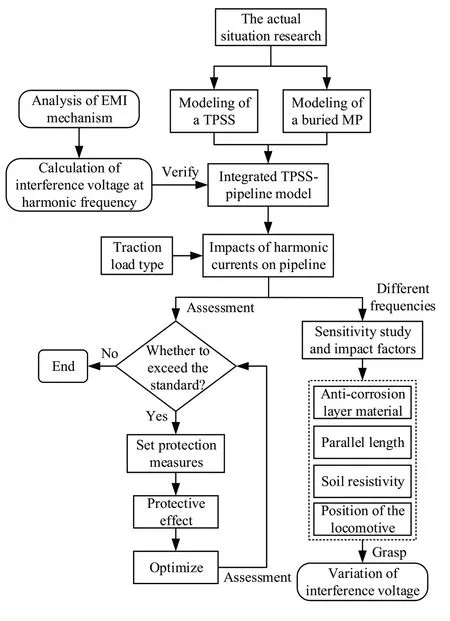
Fig.27 Flowchart for assessing EMI from AC electrified railroad harmonics to buried pipelines

5.6 Field test results and analysis

In order to further study the electromagnetic interference of electrified railway to buried metal pipeline, an existing pipeline line was selected for field test.Figure 23 shows the schematic diagram of the pipeline interference test along a railway, KP1 and KP2 are measurement points.

The variation of interference voltage at KP1 under different harmonic currents is supplemented (as shown in Fig.24).The traction load current is 210 A, the harmonic current distortion rate in working condition 1 is 2.1%, and that in working condition 2 is 6%.From Fig.24, the interference voltage amplitudes in the two working conditions are 2.98 V and 3.82 V, respectively, with an increase of 28.2%.This further illustrates that the harmonic distortion will aggravate the interference voltage of the pipeline.

Figures 25 and 26 show the variation of interference voltage at two measuring points on the pipeline.It can be seen that harmonic content exists in the interference voltage.Furthermore, the interference voltage can be significantly reduced after applying grounded drain device.The interference voltage at KP1 is reduced from 14.3 to 7.2 V.The interference voltage at KP2 is reduced from 21.6 to 6.41 V.

Through the above analysis, it can be found that the influence of harmonic on the interference voltage is significant.In this paper, the evaluation process of electromagnetic interference of AC electrified railway harmonics on buried pipelines is summarized, as shown in Fig.27, which can provide reference for practical engineering.

6 Conclusions

In this paper, it is revealed that harmonic distortion and resonance in a TPSS make the interference voltage become more serious than that caused by the power frequency.The main findings and recommendations are summarized below:

1) It is recommended to use Carson integral formula to calculate mutual impedance when using circuit method to evaluate the electromagnetic interference of TPSS harmonics to pipelines;

2) The more serious the harmonic current distortion of the traction load, the greater the interference voltage on the pipeline.In addition, the interference voltage is magnified approximately 7 times due to the resonance of the TPSS;

3) The interference voltage is positively correlated with soil resistivity, anti-corrosion layer resistivity and pipeline length.In addition, the interference voltage is sensitive to harmonics harmonic frequency;

4) After parallel connecting bare copper belts beside the pipeline, the interference voltage can be reduced by 60%.The numerical simulation can optimize the key parameter settings and selection principles.

To sum up, the effect of harmonic distortion and resonance on the interference voltage of a pipeline should be considered in the process of evaluating the AC interference.

Acknowledgements This work was supported by the National Natural Science Foundation of China (No.51877182).

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,adaptation, distribution and reproduction in any medium or format,as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.The images or other third party material in this article are included in the article's Creative Commons licence,unless indicated otherwise in a credit line to the material.If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visit http:// creat iveco mmons.org/ licen ses/ by/4.0/.