Influence of train speed and its mitigation measures in the shortand long-term performance of a ballastless transition zone

Ana Ramos · Rui Calçada · António Gomes Correia

Abstract The ballastless track is nowadays the most popular railway system due to the required low number of maintenance operations and costs, despite the high investment.The gradual change from ballasted to ballastless tracks has been occurring in Asia, but also in Europe, increasing the number of transition zones.The transition zones are a special area of the railway networks where there is an accelerated process of track degradation, which is a major concern of the railway infrastructure managers.Thus, the accurate prediction of the short- and long-term performance of ballastless tracks in transition zones is an important topic in the current paradigm of building/rehabilitating high-speed lines.This work purposes the development of an advanced 3D model to study the global performance of a ballastless track in an embankment-tunnel transition zone considering the influence of the train speed (220, 360, 500, and 600 km/h).Moreover, a mitigation measure is also adopted to reduce the stress and displacements levels of the track in the transition.A resilient mat placed in the tunnel and embankment aims to soften the transition.The behaviour of the track with the resilient mat is evaluated considering the influence of the train speed, with special attention regarding the critical speed.The used methodology is a novel and hybrid approach that allows including short-term and long-term performance, through the development of a powerful 3D model combined with the implementation of a calibrated empirical permanent deformation model.

Keywords Ballastless track · Train speed · Numerical modelling · Transition zone · Critical speed

1 Introduction

Transition zones are described by an abrupt change in the track stiffness, which leads to the development of differential settlements and the growth of dips and bumps [1, 2].Indeed,the transitions are the main source of problems and maintenance operations in the railway lines, which implies high costs [3-5] and significant concern regarding the railway infrastructure managers.

The degradation process begins with the difference in the support stiffness, increasing the dynamic wheel load, and the respective dynamic amplification of the vertical train-track interaction.This process can be an important cause of the noise generation, vibration, poor ride comfort, and high risk of derailment [6], as well as the appearance of hanging sleepers, permanent rail deformation, ballast penetration into the subgrade and cracking of the concrete sleeper and concrete slab [7, 8].Indeed, it is possible to understand that track degradation is a self-perpetuating process since the differential settlements lead to the amplification of the dynamic loads, which leads to the increase of the differential settlement [7].However, it is very difficult to model this process since the stress levels do not remain unchanged and vary along the life cycle of the structure.

The transition zones can be characterised according to the type of the transition: a track change between a ballasted track to a ballastless track, embankment to tunnel or bridge,or the presence of a box culvert or hydraulic underpass.Moreover, the transition may be due to a difference in the stiffness of the foundation soil (soft to stiff).

Currently, the ballastless track structures are a popular choice in high-speed lines due to the low maintenance operations and costs, despite the initial investment [9].Thus, the ballastless structures present a better long-term performance and lower permanent deformations, also in the transition zones.However, it is important to take special care since the performance of the slab track may be influenced by the track structure, foundation materials and train speed.Moreover, in the ballastless tracks, the deformation allowable limits are more reduced in terms of permanent deformations (when compared to the ballasted track), due to high sensitivity on deformation, and difficulty in the operations, leading to high maintenance costs.Indeed, the maintenance of the transition zones and the associated costs are significant when compared to the plain track maintenance operations.For example, in the US, $200 million are spent annually to maintain the transition zones, while in Europe about 97 million are spent on similar maintenance activities [10].Moreover, in the Netherlands, the maintenance activities on the tracks in transition zones are performed up to four-eight times more often than those on “normal/open” tracks [11, 12].Thus, the long-term performance of the ballastless tracks in transition zones requires advanced numerical modelling and special care to predict and avoid the concrete tracks and differential settlements.This means that a correct assessment of the substructure settlement induced by the train requires the development of powerful and suitable models and methodologies capable of describing permanent deformation under repeated dynamic loading [13].Indeed, the soil settlement is unavoidable, but it can be predicted and manageable [9].Moreover,to ensure the operation safety and reliability of high-speed railway lines, the criteria on the track geometry irregularity and infrastructure stability should be considered [14].

Because of the increase in the popularity of ballastless railway structures, the number of transitions with this railway system is also growing.However, there are very few works about this theme since it is expected that the ballasted track shows a worst short- and long-term performance[15].Indeed, most of the works are developed in the scope of the transitions between ballasted and ballastless tracks[16-19], or between a ballasted track and stiffer structure such as a box culvert or a bridge [6, 12, 20-27].The key idea of the transition zones is to soften and minimise the impact caused by the discontinuities along the track [24].The main goal is to choose an efficient approach capable to ensure a smooth transition between the soft and stiffparts of the structure.Based on these assumptions, it is possible to assume that there are, currently, very few works about this theme in the scope of the ballastless track transition zones, including mitigation measures.This work introduces a study about the short- and long-term performance of a ballastless track in transition zone with the influence of the train speed (including the critical speed) and the impact of a mitigation measure using an advanced and hybrid approach to include the short- and long-term performance.Indeed,with increasing train speed, there is an acceleration of the degradation of the geomaterials, causing excessive settlement [28].This situation is even worst in transition zones.In this case, the transition is between an embankment and a tunnel, with a significant change in the support of the structure.This modelling includes the vehicle-track and supersubstructure interactions.A hybrid approach was used to analyse the performance of the track considering different train speeds, which also include the critical speed: 220, 360,500 and 600 km/h.A mitigation measure is also presented,and its efficiency is analysed with the variation of the train speed.The short-term performance is analysed through a powerful 3D finite element model developed in ANSYS,and the permanent deformation is determined based on the implementation of a calibrated empirical permanent deformation model to simulate the track’s degradation.

2 Numerical model and methodologies

This work purposes the study of the influence of train speed on a ballastless track in a transition zone.Indeed, with the increase of the train speed, there are expected an amplification of the dynamic effects generated by the passage of the train.These dynamic effects are due to the stiffness difference in the transition zone allied to the dynamic effects of the train speed.Indeed, the tunnel presents a higher stiffness when compared to the embankment.This difference leads to the appearance of differential settlements, increasing the dynamic excitation of the train components, which have an impact on the dynamic amplification of the train-track interaction.

2.1 Numerical model

The numerical model represents a 3D ballastless track constituted by the rails, railpads, concrete slab, hydraulically bonded layer (HBL) and a substructure that includes the frost protection layer (FBL) and subgrade.This means that the model represents the exact geometry of the problem,without simplifications and omissions, The full and detail characterisation of these materials can be found in Ref.[2].The main properties are described in Table 1, whose values are based on a previous calibration developed by Ramos et al.[29].This calibration was based on two-step processes (short-term and long-term calibration), and it was performed based on the experimental results obtained in a full-scale physical model (2.2 m long) of a ballastless track.The structure was submitted to more than 3 million load cycles, which allows for acquiring a significant amount of data regarding the development of permanent deformation.In the short-term calibration, the material properties were adjusted (Poisson’s ratio and Young modulus of the geomaterials and rail pad).The long-term calibration includes the adjustment of the permanent deformations measured on the linear variable differential transformers (LVDTs).Based on this calibration the 3D slab track model was extended to simulate a transition between an embankment and a tunnel.The tunnel is simulated with the inclusion of rigid supports under the HBL.Thus, it is possible to have a full confidence in the obtained results.

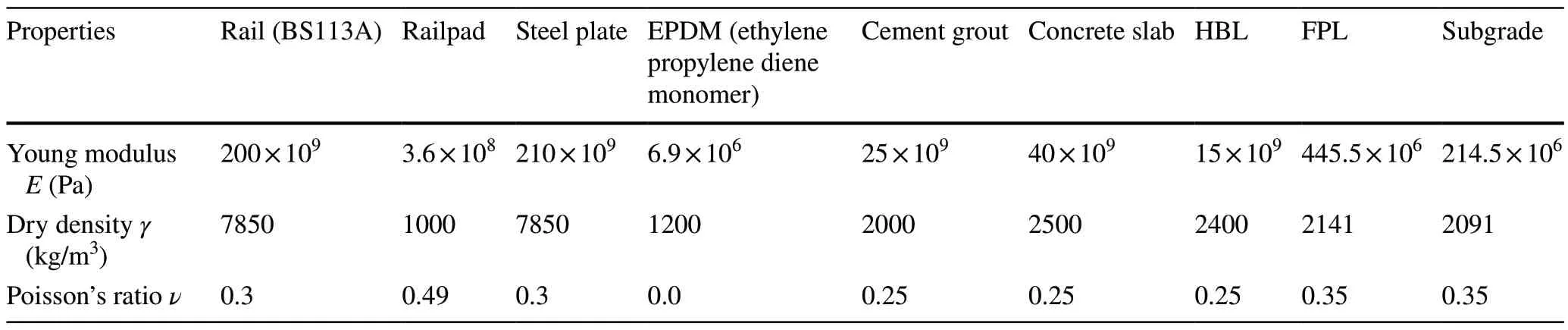
Table 1 Properties of the materials (adapted from Ref.[2])

Fig.1 Numerical model: a global view; b detail of the transition between the embankment and the tunnel

In this analysis, the damping values were determined based on the Rayleigh damping matrix.The αiandβiparameters were defined based on a numerical receptance analysis.From the results, a range of frequencies between 5 and 200 Hz was adopted.This range is considered enough to obtain a correct response of the track.

The developed numerical model is depicted in Fig.1,where variablehrepresents the height/thickness of the layer.The model presents a total length of 53.1 m and includes the embankment (with 31.65 m) and the tunnel (with 21.25 m).To increase the efficiency of the model, symmetric conditions were considered.Moreover, the mesh was also optimised to reduce the time of calculus.The distance between the symmetric plane and the vertical boundary is 6 m.The positionx= 0 m corresponds to the transition between the embankment and the tunnel.

The analysis was performed considering the passage of the PortugueseAlfa Pendulartrain with different train speeds: 220, 360, 500 and 600 km/h.The properties of the train and model are presented in Table 2 and Fig.2.In this analysis, the bogies, primary suspension, mass, and the axle of the wheelset were modelled, as well as the Hertzian stiff-ness to simulate the interaction between the vehicle and the track.This simplification of the train model is considered enough since the excitation frequencies are within the mean range of frequencies [30].It is important to highlight that the properties of the track were divided by two since only half of the track was modelled.

Regarding the load, a constant value of 67.5 kN (135/2)was adopted.To simulate the short- and long-term behaviour of the track, the passage of the first 4 bogies was simulated.Indeed, from the 4th bogies, there is a repetition of the geometry of the train.

Table 2 Characteristics of the Alfa Pendular train adopted in this study (adapted from Ref.[2])

Fig.2 Finite elements model (vehicle and rail)

To avoid spurious reflections and attenuate the waves that impinge the vertical boundaries, viscous dampers were adopted and placed in the FPL and subgrade materials using theLysmerformulation.Indeed, this approach has been used in the scope of 3D modelling with good results.

Regarding the modelling, the materials were modelled with solid elements with 8 nodes using linear elastic models.Moreover, contact elements were implemented between the train and track to simulate the interaction between the two bodies and between the HBL and FPL (super and substructure) to simulate the “detachment” between both elements.Indeed, this is tentative to replicate the real response of the track in transition zones considering a slab track system,which is practically inexistent.More details about the modelling of the contact elements can be found in Ref.[2], which include information about the normal penalty stiffness factor.The dynamic analysis was performed in the software ANSYS using the Newmark-Raphson method with a time step equal to 0.002 s.

3 Influence of the train speed

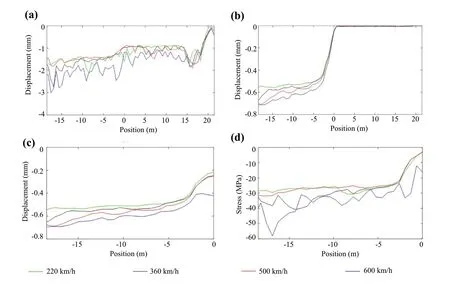
Fig.3 Maximum displacements induced in the top of a rail, b concrete slab, c subgrade, and d maximum stresses induced in the top of subgrade

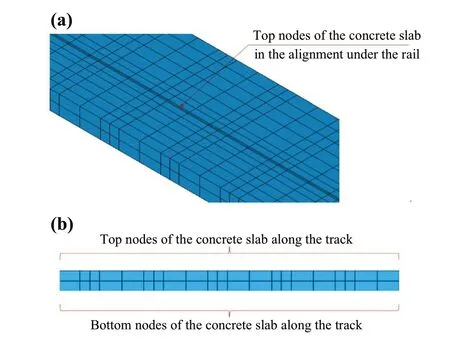
Fig.4 Location of the selected nodes on the concrete slab: a 3D view; b 2D view

This work aims to analyse the influence of the train in the dynamic response of a ballastless track in a transition zone.Thus, four different train speeds were simulated: 220, 360,500 and 600 km/h.Indeed, these different and significant speeds were tested in order to simulate the performance of a high-speed line in a transition zone.The higher speed(600 km/h) was selected to study the influence of the critical speed in the behaviour of the rail track since strong amplification of track response is expected.Given the adopted properties of the substructure materials (described in Table 1), it is possible to understand that the geomaterials can be classified as very good materials with high values of Young modulus.This means that high values of the critical speed should be simulated.

The critical speed can be described as the velocity of a moving non-oscillating load that conducts to the higher amplification of the dynamic response, i.e., the speed of the load that gives rise to a resonant like problem.The critical speed is fully dominated by the properties of wave propagation in the embankment-ground system and of the bending wave propagation in the track [31].

Based on the work developed by Costa et al.[32], the critical speed can be expeditiously calculated through the dispersion curves.This method is an approximation, but it is very effective and efficient.Nevertheless, when the ground is homogenous, it is possible to ignore the track characteristics since the critical speed would be the same, regardless of the type of railway structure [31].In the analyses presented in this work, and considering these assumptions, the critical speed of the ballastless track was determined based on the shear wave velocity of the substructure and is close to 700 km/h.This means that, when the train speed runs above 70%-75% of the critical speed, the response of the track(stresses, strains and displacements) increase significantly[33, 34].Indeed, 75% of critical speed can be assumed as the practical speed limit of railway tracks.This means that the value of 500 km/h is perfectly acceptable as a practical speed limit.The value of 600 km/h is a little higher but still below the critical speed.Indeed, currently in Europe, this speed is unrealistic, but its results are presented to show the ability of the method to capture the behaviour of the structure when submitted to this range of speeds.Furthermore,higher amplifications due to the influence of the dynamic mechanisms of the stresses and permanent deformations are expected [15, 35].This work tries to obtain and understand the magnitude to the response of the track with the train speed.

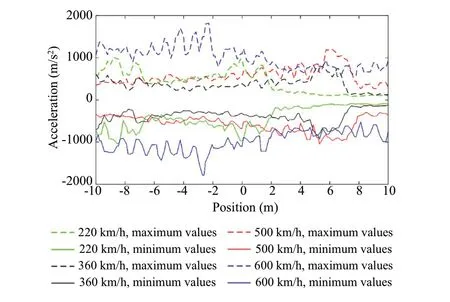
Fig.5 Rail acceleration

3.1 Short-term performance

The short-term performance includes the evaluation of the displacements, strains and stresses induced in the elements of the track during the passage of theAlfa Pendulartrain.

The first results are related to maximum displacements obtained in the top of the rail, concrete slab, and subgrade under the alignment of the load (Fig.3).An exemplification of the selected nodes to study the performance of the track on the concrete slab is presented in Fig.4.

In the analysis of Fig.3, all the results show that the displacements increase with the train speed.In the case of the rail, the train speed of 600 km/h increases the magnitude and variation of the displacements (the results are less soft when compared to the remaining speeds) the magnitude of the displacements also increases in the concrete slab and subgrade.Moreover, the maximum stresses induced in the subgrade were determined (Fig.3d).Again, the results show that the train speed closer to the critical speed increases the stresses and strains in the subgrade.In the case of the stresses, there is a peak stress atx= - 17 m, which is almost the double of the stress levels considering lower speeds.

Furthermore, the vertical accelerations on the top of the rail were evaluated (Fig.5).The results show that, when the train speed is far from the critical one, the acceleration results have almost the same magnitude.However, when the train speed increase to 600 km/h, there is a significant amplification of the acceleration at the rail level.Moreover,the vertical accelerations were also obtained in the top and bottom elements of the concrete slab and HBL since these are the elements that assure the continuity of the track.The results are presented considering the maximum and minimum values of the vertical acceleration along the track under the loading alignment.

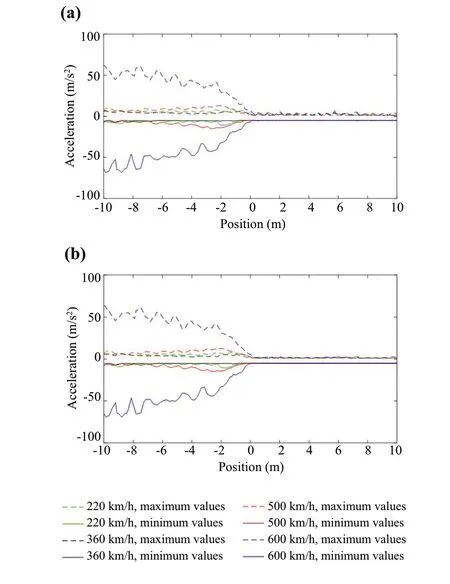
Fig.6 Vertical accelerations on the top nodes of a concrete slab and b HBL

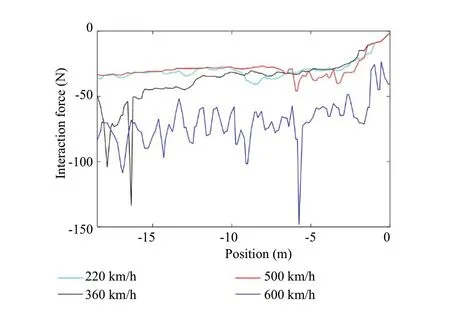
Fig.7 Maximum HBL-FPL interaction force

Fig.9 Vertical stresses at HBL: a top; b bottom

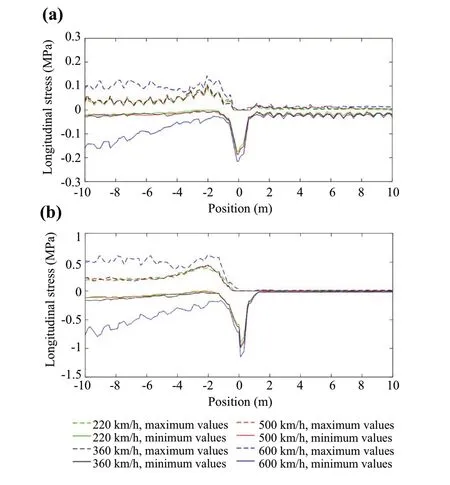
Fig.10 Longitudinal stresses at the HBL: a top; b bottom

Again, the results show that the accelerations increase with the train speed.However, this increase is significantly higher in the concrete slab and HBL (Fig.6), mostly before the transition (x= 0 m) when the train speed is 600 km/h.In this case, the accelerations go beyond the acceptable values which usually are below 10 m/s2.The remaining speeds lead to acceptable values.Moreover, the results also show that the maximum and minimum values of the vertical acceleration at the top nodes of the concrete slab and HBL are almost equal.As expected, the results also show a decrease in the vertical acceleration along the transition.

Besides the accelerations, the interaction forces are essential to understand the magnitude of the response of the track and to study the problem related to the “detachment”phenomenon between the HBL and the FPL (Fig.7).The results (under the loading alignment) show that, when the train speed is closer to the critical one, there is a significant increment in the interaction forces.

The stresses induced on the superstructure were also evaluated in detail.The maximum and minimum values of the longitudinal and vertical stresses were obtained along the transition at the top and bottom nodes under the loading alignment regarding the concrete slab and HBL.Each point of the diagrams (Figs.8, 9, 10) corresponds to the nodal stresses of the finite elements.

Regarding the concrete slab, the longitudinal stresses show a peak stress at the transition concerning the maximum values.The minimum values show a significant decrease at the transition.The stress results do not show a significant increase of its magnitude with the train speed.The results show important differences at the top and bottom stresses in the concrete slab.The magnitude of the stresses is 10 times higher at the top when compared to the bottom of the material.

In the HBL, it is possible to identify clear peaks at the transition in the vertical and longitudinal directions.The results show that the train speed has no significant influence on the increase of the stresse magnitude.However, in the longitudinal stresses, before the transition, the higher train speed imposes higher stresses.

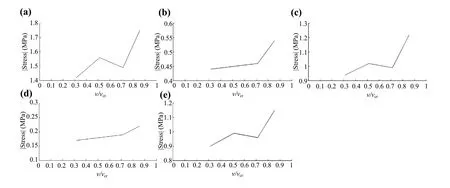
Fig.11 Evolution of stresses along with ratio of the train speed in concrete slab and HBL: a longitudinal maximum stresses on the concrete slab(top); b vertical minimum stress on the HBL (top); c vertical minimum stress on the HBL (bottom); d longitudinal minimum stresses on the HBL (top); e longitudinal minimum stresses on the HBL (bottom)

Table 3 Evolution of the increment of the stresses with the train speed in concrete slab (unit: MPa)

This analysis is essential since the concrete slab and HBL are the elements that connect the embankment and the tunnel, which means that they assure the continuity of the track, along with the rail.Therefore, the concrete slab and HBL are submitted to a complex stress field, they may be aggravated due to the variation of the stiffness of the track in the transition.The results also show that, in the tunnel, the vertical stresses on the top nodes of HBL are slightly higher when compares to the flexible zone for all the tested train speeds.Moreover, the results also show that the stress levels at the bottom of HBL are higher than at the top.This is due to the contact forces that are established between the super and substructure (HBL and FPL,respectively).

The evolution of the absolute values of the stresses on the concrete slab and HBL with the ratio of the speed(train speed/critical speed ) are presented in Fig.11.The results show the increase of the stresses until the maximum ratio studied (close to 0.9).

To understand the magnitude/evolution of the stresses at the transition zone according to the train speed, the results were compared and are described in detail in Tables 3 and 4.

Fig.12 Evolution of the increment of the stresses with the train speed

The reference speed to implement this analysis is the lower one: 220 km/h.Figure 12 shows that this evolution presents the same tendency and does not vary with the element in analysis, type of stress, or position of analysis(top and bottom).

3.2 Long-Term performance

To correctly predict the soil settlement of the track (especially in a transition) it is necessary to understand the long-term performance of the geomaterials when submitted to millions of load cycles [36, 37].However, the incorporation of this type of analysis in complete models of the track is still a very unexplored topic [38].This type of analysis is important to have a total integration of the short-term and also long-term performances since the permanent soil settlement has a significant influence on the frequency of the maintenance operations and respective costs.Yet, it is totally influenced by short-term performance.Considering the importance of the topic, several authors have been working on different methodologies to predict and study permanent deformation, especially in transition zones [3, 25, 39-42].

The developed methodology can be adapted and implemented considering different models, geometries and materials and permanent deformation models.

In this analysis, the prediction of the permanent deformation is only carried out on the FPL and subgrade, which are the geomaterials.The permanent deformation is determined by applying the empirical model developed by Chen et al.[43].

Fig.13 Developed methodology: prediction of the soil settlement

The constants used to describe the empirical permanent deformation model were obtained in a previous work developed by Ramos et al.[29].The determination of these parameters was based on the calibration process (longterm calibration).As mentioned previously, a ballastless track structure (2.2 m long) was submitted to more than 3 million load cycles (using a full-scale facility), which allows to measure the development of the permanent deformation using the LVDTs placed in specific positions on the track.The numerical results (short- and long-term)were compared to the experimental ones and were calibrated based on the 3D models of the track and the implementation of the empirical permanent deformation model:where the parameters,Bandaare the material constants of the model;pais the atmospheric pressure (100 kPa);mandsare defined by the yielding criterionq=s+m∙p;Nis the number of loading cycles;piniandqiniare the initial stress state andpamandqamare the stress levels induced in the subgrade during the passage of the train.Thus, it is possible to conclude that this is a very complete and complex model since depends on different parameters but is very easy to implement numerically [15, 36].

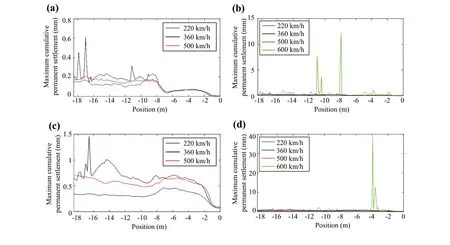
Fig.14 Maximum cumulative permanent settlement: a in the FPL with the train speed between 220 and 500 km/h; b in the FPL with the train speed between 220 and 600 km/h; c in the subgrade with the train speed between 220 and 500 km/h; d in the subgrade with the train speed between 220 and 600 km/h

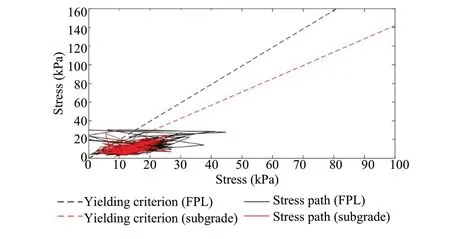
Fig.15 Example of the stress path induced on the FPL and subgrade when x = -13 m

The developed methodology is based on the number of load cycles and mostly it is dependent on the stress levels submitted in the substructure induced by the passage of the train (Fig.13).In this case, each cycle (N) corresponds to the passage of 1 of the 24 axles of theAlfa Pendulartrain.In this methodology, and considering the geometry of the track, a 3D numerical model of the vehicle-track system is developed in the software ANSYS.Based on this model,a dynamic analysis is performed with the inclusion of the vehicle-track interaction and contact elements between the super (HBL) and substructure (FPL) to simulate the“detachment” of the track.From the numerical results,the stresses in the substructure (FPL and subgrade) are obtained in all directions and in all elements and nodes.These stresses are exported to MATLAB to predict the permanent deformation based on an empirical permanent deformation model.This permanent deformation can be,then, inputted into the 3D model to simulate the track degradation.This simulation in particular will not be analysed in this work.

Fig.16 Maximum cumulative permanent settlement: a in the substructure (FPL + subgrade) with the train speed between 220 and 500 km/h; b in the substructure (FPL + subgrade) with the train speed between 220 and 600 km/h

Fig.17 Distribution of the maximum cumulative permanent settlement (FPL)

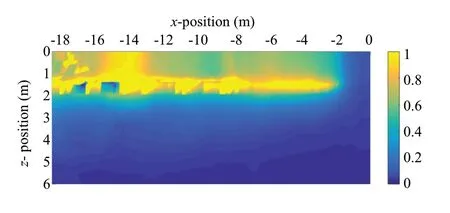
Fig.18 Distribution of the maximum cumulative permanent settlement (subgrade)

In this analysis, each curve of the permanent deformation corresponds to 1 million load cycles.Thus, during the calculation of the permanent deformation, it is possible to assume that stress conditions remain unchanged, which means that they are constant.

Despite the importance of the permanent deformation,the results are analyzed in terms of cumulative permanent settlements to have the magnitude of the track settlement:

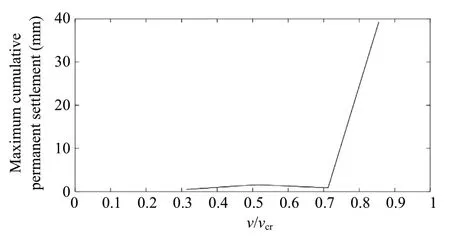
Fig.19 Distribution of the maximum cumulative permanent settlement (subgrade)

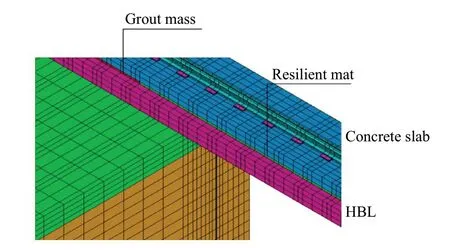
Fig.20 Numerical model with the resilient mat

whereicorresponds to the number of elements that constitute a certain material;Hs;icorresponds to the thickness of each element (in m); εp;iis the permanent deformation at the center of each element andδis the cumulative permanent deformation (in m).

Following this methodology, the maximum cumulative permanent settlements were obtained in the FPL, subgrade and the substructure (FPL + subgrade) in the alignment under the load.

Figure 14 shows the results on the subgrade and FPL.With the increase in train speed, there is an increase in permanent settlements.The permanent settlements are higher when the train speed is 360 km/h when compared to 500 km/h.However, the differences are not substantial.The increase in the permanent settlements is significantly higher when the train speed is close to the critical speed.In the FPL the results are still below the allowable deformation in slab tracks in high-speed lines (30 mm),but, in the case of the subgrade, the results are above the30 mm, which can be a problem.Moreover, the settlements are higher in the subgrade when compared to the FPL.Although the magnitude of the stresses is greater at the FPL, the strength properties of the track influence the development of permanent deformation such as the cohesion and friction angle.In the subgrade elements, the stress paths are closer to the yielding criterion inducing higher settlements, as depicted in Fig.15.

Table 5 Properties of the resilient mat

Moreover, to understand the magnitude of permanent settlements on the substructure, the results of the FPL and subgrade were analyzed together (Fig.16).The results show the previous tendencies.When the train speed is below 500 km/h, the maximum cumulative permanent settlement is close to 1.5 mm.However, when the train speed is higher and equal to 600 km/h, the results are above the allowable limit (30 mm) in high-speed lines.

The previous results correspond to analyses considering the alignment under the load.However, it is important to understand the distribution of the permanent settlements along with the surface of the subgrade and FPL.The results depicted in Figs.17 and 18 correspond to the distribution of maximum cumulative permanent settlement.Figures 19 and 20 show that the maximum settlement does not occur in the alignment under the subgrade but under the end of the concrete slab.This is due to the influence of the initial stress state levels that are higher under the concrete slab and lower outside the concrete slab.With lower initial stress levels, the stress paths are closer to the yielding criterion, inducing higher permanent deformation levels.

The evolution of the maximum cumulative permanent settlement on the substructure (FPL + subgrade) with the speed ratio (train speed/critical speed,v/vcr) is presented in Fig.19.The results show the increase of the permanent settlement until the maximum ratio studied (close to 0.9).Indeed, between 0.7 and 0.9, there is a significant increase.This means that when the train speed is close to the critical speed, the long-term performance of the track may decrease drastically.

Fig.21 Displacements induced in the a slab and b subgrade considering the resilient mat

4 Mitigation measure: influence of the resilient mat

In order to improve the performance of the ballastless track in a transition zone between an embankment and a tunnel, a resilient mat was tested and placed between the slab track and HBL (in the original position of the grout mass with 40 mm thickness) to smooth the displacements,as well as the stress peak.The resilient mat (with a thickness of 40 mm) was placed in the tunnel and in the first metre of the embankment immediately before the transition (Fig.20).This mat can be understood as a mitigation measure of the ballastless track in a transition zone.

This mat can be characterised as a soft resilient layer that is often composed of natural rubber.This material presents very good dynamic properties and gives flexibility under the concrete slab.This allows for balancing the stiffness between the embankment and the tunnel.The performance or influence of the mat is evaluated according to train speed and considering the short- and long-term performance of the track.

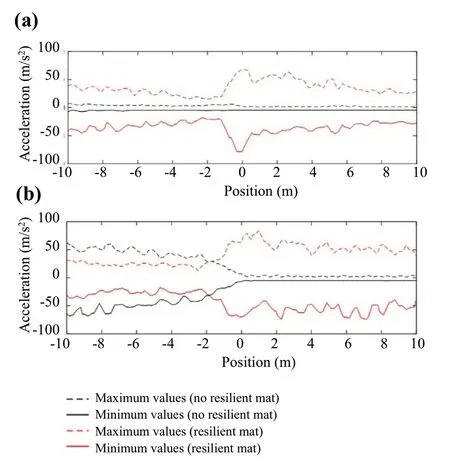
Fig.22 Accelerations on the top nodes of the concrete slab: a 360 km/h; b 600 km/h

Fig.23 Acceleration on the top nodes of the HB0L: a 360 km/h; b 600 km/h

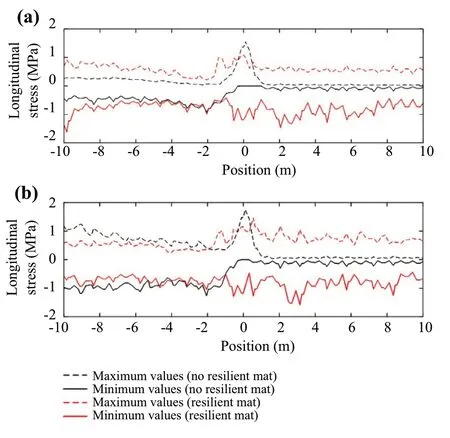
Fig.24 Longitudinal stresses on the top nodes of the concrete slab: a 360 km/h; b 600 km/h

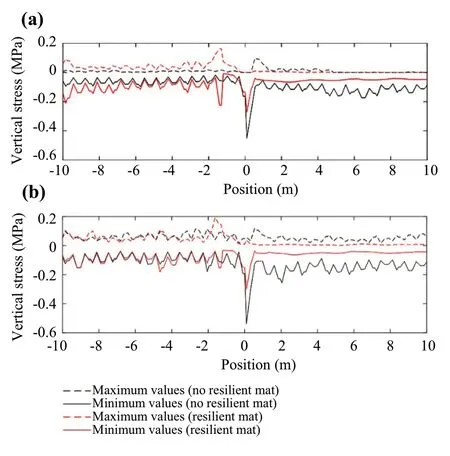
Fig.25 Vertical stresses on the top nodes of the HBL: a 360 km/h; b 600 km/h

As is possible to observe in Fig.20, the grout mass in the tunnel zone was replaced by the resilient mat.The thickness keeps unchanged (40 mm) in order to not modify the geometry of the track.The resilient mat was also modelled with solid elements with 8 nodes and the stiffness of the element was defined based on an iterative process in order to balance the displacements.The properties of the resilient are given in Table 5 and were obtained in the catalogue Trackelast-slab track mats, along with the density.Regarding the damping properties, an hysteretic dampingξof 2.5% was adopted based on the work developed by Zbiciak et al.[44].A Poisson ratio equal to 0 was implemented since only vertical deformations are expected.

4.1 Short-term performance

Considering the geometry and the properties of the resilient mat, the displacements of the slab and subgrade were obtained in the top nodes of each material under the load alignment.The results depicted in Fig.21 show a positive contribution of the resilient mat in the attenuation of displacements, mostly in the concrete slab.However,the differences are also visible in the subgrade for each train speed.The results show a smoother transition (with a resilient mat) when compared to the situation without a resilient mat where the displacements are zero from the transition atx= 0 m for the concrete slab.

Despite the importance of displacement analysis, it is crucial to evaluate the accelerations and the stresses induced in the concrete slab and HBL.In this analysis,two train speeds were selected: 360 and also 600 km/h, in order to evaluate the combined effect of the critical speed and the resilient mat to attenuate the stresses.

Regarding the accelerations (Figs.22, 23), the results show a bad performance of the track with the resilient mat,especially when the train speed is closer to the critical speed.In some cases, the acceleration levels are far from the acceptable values (10 m/s2).

The results depicted in Fig.24, show a reduction of the longitudinal stress peak (maximum values) at the top of the concrete slab at the transition (x= 0 m) for each train speed.This means that there is a mitigation of the stresses,despite its increment after the transition.The magnitude of the attenuation is similar for reduced and higher train speeds.

Figure 25 shows an attenuation of the vertical stresses on the top nodes of HBL.Thus, the peak does not disappear, but it is attenuated for each train speed.The magnitude of the attenuation is higher when the train speed is closer to the critical one.

4.2 Long-Term performance

Regarding the long-term performance, considering the mitigation measure with a resilient mat, no big differences are expected concerning the long-term performance,except in sections close to the transition since the resilient mat is placed in the first meter of the embankment before the transition.Indeed, Fig.21b shows some differences in the displacements at the subgrade level in sections close to the transition.

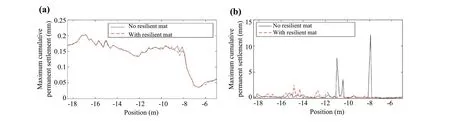
Fig.26 Maximum cumulative permanent settlements with and without a resilient mat in the FPL: a 500 km/h; b 600 km/h

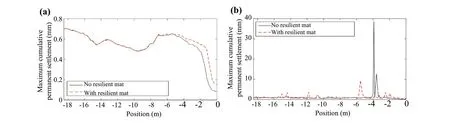
Fig.27 Maximum cumulative permanent settlements with and without a resilient mat in the subgrade: a 500 km/h; b 600 km/h

The results regarding the long-term performance are depicted in Figs.26 and 27.These results were obtained following the same methodology explained in Sect.3.2.

In this case, only the results associated with higher speeds are presented because higher differences are expected.In the FPL, when the train speed is 500 km/h,there are very few differences between both scenarios.However, when the train speed is 600 km/h, there are significant differences with and without the resilient mat.Indeed, the cumulative permanent settlement peaks disappear, improving the performance of the track.

In the subgrade, when the train speed is 500 km/h, there are some differences between both scenarios, mostly close to the transition (approximately 4 m before the transition),which is expected since the resilient mat was placed in this zone of the embankment.However, when the train speed is 600 km/h, there are significant differences comparing the scenarios with and without the resilient mat.Indeed, the peak values close to the transition disappear, improving the performance of the track.

5 Conclusions

This paper presents a study about the performance of a ballastless track in transition zones with the influence of the train speed, including the critical speed.To do so, a novel and hybrid approach developed was used to simulate the track degradation.A powerful and advanced 3D FEM model was developed in ANSYS, which allows the evaluation of the short-term performance of the track.The soil settlement is simulated through the implementation of a calibrated empirical permanent deformation model.

The short-term performance was evaluated through the strains, stresses and displacements induced in the main elements of the track considering the passage of the first four bogies of the Alfa Pendular train: rail, concrete slab, HBL,FPL and subgrade.The results show a higher concentration of stresses in the transition zone in the concrete slab and HBL, which are the elements that assure the continuity of the track.Moreover, the stresses and displacements increase with the train speed.However, the magnitude of the increase is significantly higher when the train speed is closer to the critical speed (600 km/h).

The long-term performance was evaluated through the permanent settlement induced in the FPL and subgrade (substructure).The results were evaluated with the variation of the train speed and show that, along with stress levels, the settlement of the substructure is significantly higher when the train speed is 600 km/h.Indeed, the maximum cumulative permanent settlement induced in the substructure is above the allowable limit with a train speed of 600 km/h.Regarding the remaining speeds, the permanent deformation increased, but the magnitude was not significantly higher.

This work also introduces the importance of the resilient mat in the scope of the transition zones and influence of the train speed.

Regarding the mitigation measure, the importance of the resilient mat in the scope of the transition zones and influence of the train speed is very inexistent and was evaluated in this work considering the short, but also the longterm performance.The benefits of the resilient mats are not straightforward since there some advantages related to the smoothness of the displacements along the track but may amplify the stress levels.However, the results show a reduction of the peak’s stresses at the transition for all the train speeds.This means that there is a mitigation of the stresses,despite its increment after the transition, in some cases.Moreover, there is a contribution of the resilient mat in the attenuation of displacements, mostly in the concrete slab.However, the differences are also visible in the subgrade for each train speed.In terms of accelerations, the results show that the resilient mat, with the increase in the train speed, may show a lower performance since the acceleration levels are far from the allowable values (10 m/s2).About the long-term performance, the results show that, when the train speed is more reduced, there are no significant differences between the scenarios with and without a resilient mat.However, when the train speed increase, the resilient mat is able to reduce the peaks of the permanent settlements in sections close to the transition zone.

Thus, this work allows the development of a powerful tool capable to perform parametric studies considering different mitigation measures and transition zones.Moreover, it introduces an innovative approach to study mitigation measures capable to increase the performance of the transition zones.

Acknowledgements This work was partially carried out under the framework of In2Track3, a research project of Shift2Rail.This work was also partly financed by FCT/MCTES through national funds (PIDDAC) under the R&D Unit Institute for Sustainability and Innovation in Structural Engineering (ISISE), under reference UIDB/04029/2020.It has been also financially supported by: Base Funding-UIDB/04708/2020 of the CONSTRUCT-Institute of R&D in Structures and Construction-national funds through the FCT/MCTES (PIDDAC).

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made.The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visit http:// creat iveco mmons.org/ licen ses/ by/4.0/.