Inconsistent effect of dynamic load waveform on macroand micro-scale responses of ballast bed characterized in individual cycle: a numerical study

Longlong Fu · Yuexiao Zheng · Yongjia Qiu · Shunhua Zhou

Abstract Cyclic load is widely adopted in laboratory to simulate the effect of train load on ballast bed.The effectiveness of such load equivalence is usually testified by having similar results of key concerns of ballast bed, such as deformation or stiffness, while the consistency of particle scale characteristics under two loading patterns is rarely examined, which is insufficient to wellunderstand and use the load simplification.In this study, a previous laboratory model test of ballast bed under cyclic load is rebuilt using 3D discrete element method (DEM), which is validated by dynamic responses monitored by high-resolution sensors.Then, train load having the same magnitude and amplitude as the cyclic load is applied in the numerical model to obtain the statistical characteristics of inter-particle contact force and particle movements in ballast bed.The results show that particle scale responses under two loading patterns could have quite deviation, even when macro-scale responses of ballast bed under two loading patterns are very close.This inconsistency indicates that the application scale of the DEM model should not exceed the validation scale.Moreover, it is important to examine multiscale responses to validate the effectiveness of load simplification.

Keywords Railway ballast · Particle movements · Contact distribution · Waveform sensitivity · 3D discrete element method

1 Introduction

Discrete element method (DEM) has been applied in modelling ballast for decades.The application of DEM enables us to observe the ensemble of ballast particles [1, 2].In DEM modelling, each particle serves like a sensor to obtain the tremendous details in ballast bed, including inter-particle contact force [3, 4], particle movements [5, 6], etc.Besides, various influence factors and complex conditions can be well-controlled in DEM modelling.A key concern of modelling ballast bed is to validate the effectiveness of DEM model.Generally, a numerical model of ballast bed can be validated by comparing with the results from laboratory or in situ check tests.In laboratory test, it is difficult to reproduce train load, especially high-speed train load.Hence, cyclic load is widely adopted to simulate the effect of train load in experimental study of ballast behavior [7,8, 9] or ballast bed responses [10, 11], especially for tests with representative elements, such as the triaxial test, direct shear test, and ballast box test.The effectiveness of such load equivalence is usually testified by having similar results of key concerns of ballast bed, such as deformation [12],stiffness [13] or strength [14, 15, 16], sleeper displacement[17], and acceleration [18], while the consistency of particle scale characteristics under two loading patterns is rarely examined.Since the same or similar dynamic behaviors of ballast bed from limited cases could result from very different microscopic processes, numerical modelling without examining particle scale responses tends to be insufficient in well-understanding the microscopic behaviors of ballast bed [5] and furtherly the equivalence of train load and cyclic load.

The field or laboratory measurement of ballast particles’behavior is the pre-condition to validate a DEM model of ballast bed.Initially, wired accelerator was employed to capture the acceleration characteristic in ballast bed [19, 20].Recently, wireless sensing stone in particle size has been employed to characterize the movement of individual particles in ballast bed [21, 22].The obtained ballast particle movements show great potential in nondestructive disease identification [23], fouling evaluation [22, 24], and reinforcement design [25] of ballast bed.Ballast movements measured by sensing stone provide particle-scale indicators to validate the DEM model concerning railway ballast [5,26].By now, ballast particle movements have been obtained under train load in situ [23].In laboratory test, ballast particle movements are obtained mainly under cyclic load [6,27], rarely under train load [28], while DEM modelling of ballast bed is validated mainly by particle movements obtained under cyclic load [5, 6].This owes mainly to that laboratory test is usually easily controlled and more productive in data collection.Besides, a representative segment is usually adopted in DEM modelling due to the limitation of computation capacity of computers, whose constraints are more similar to those of laboratory test [2, 4, 15, 29].In order to well-understand and use the load simplification in exploring the micro-mechanism of ballast bed behavior, the consistency of particle scale characteristics under cyclic load and train load is worth being examined.

In this study, a full-scale ballast bed model with a half sleeper is built via PFC3D and validated by the dynamic responses monitored by high-resolution sensors in a previous model test [5, 15, 27].Then, two widely used waveforms,i.e., cyclic load and train load, are applied in the numerical model.According to the equivalence of loading effect,cyclic load and train load are assigned the same magnitude and amplitude for comparison [12].Then, we obtained not only macroscopic responses like dynamic stiffness and subballast stress, but also statistical characteristics of inter-particle contact force and particle movements in ballast bed.By comparing the values of each indicator under two loading patterns, the influence of loading pattern on multiscale responses is discussed.

2 DEM modelling of ballast bed

Considering the symmetry of ballast bed and the loading capacity, a half sleeper model is built in laboratory, as shown in Fig.1a.The establishment details and test schemes of the full-scale laboratory test have been reported in previous work [27, 29].The gradation of reproduced ballast conforms to the first class gradation requirements of the Chinese criterion ‘Railway Ballast (TB/T 2140-2008)’, as shown in Fig.1b.Cyclic load is applied by an electrohydraulic servo actuator.The loading frequency varies from 1 to 18 Hz, with a loading magnitude of 30 kN.

The half sleeper model shown in Fig.1 is built via PFC 3D, as shown in Fig.2.Since single track railway line is considered, the bottom of ballast bed is about 2.5 m in width (alongxdirection), with a slope of 1:1.75.Ballast aggregate beneath the sleeper is approximately 0.35 m in height (along thezdirection) and 0.6 m in thickness (along theydirection).The model contains more than 11,000 ballast particles, where particles are reproduced on the basis of the profiles scanned from real ballast.Here, three dominant ballast shapes are considered: quasi-cubic type,flat type and elongated type, whose aspect ratios are about 2:2:1, 1:1:1 and 2:1:1, respectively.The shape database includes shape samples from 20 real ballast particles.For each diameter range shown in Fig.1b (for example 25-36 mm), particles are generated with shape randomly assigned from the shape database, whose size follows a normal distribution.The simulation accuracy of ballast particles is governed mainly by the ratio of the smallest to largest pebble and the distance (angular measure) between overlapping pebbles in the bubble pack algorithm [30].In this study, the ratio and distance are taken as 0.4 and 100°,respectively.

Fig.1 Model setup in previous laboratory test [5, 27]: a laboratory model test with semi-sleeper; b ballast gradation

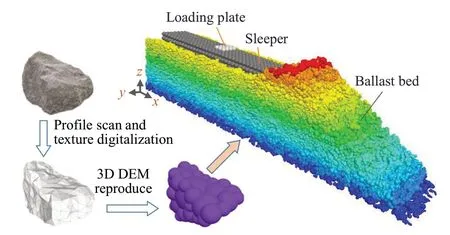
Fig.2 The process of reproducing ballast particles and DEM model of ballast bed

The ballast bed is filled in three layers, where enough ballast particles are generated and preloaded for each layer.The final bulk density of ballast bed is controlled no lower than 1750 kg/m3, which conforms to the density requirement in the Chinese criterion ‘Railway Ballast (TB/T 2140-2008)’.The sleeper is composed of mono-size balls in rectangular arrangement, where the parallel contact model is adopted to allow deflection of the sleeper.A loading plate is fixed on the sleeper at the sub-rail location.Theoretically, the symmetry plane of a sleeper is deemed having no rotation under symmetric wheel load, and balls at the cut-section of the half sleeper are allowed only free vertical translation.The numerical parameters of ballast are calibrated by triaxial test [5].The whole numerical model is validated by macro-scale responses obtained in laboratory test [27],including sub-ballast stress and dynamic stiffness of the ballast bed.The model parameters are finally determined as shown in Table 1, where damping coefficients take the values suggested in Ref.[5].Four walls are set in DEM model to simulate the boundary condition shown in Fig.1b: The normal and tangential contact stiffnesses for the two walls along theydirection are all 2.3 × 106N/m, which are set as 1 × 107N/m for the other walls.

Figure 3 shows the comparison of macroscopic responses obtained in laboratory test shown in Fig.1a and the DEM model shown in Fig.2.It is observed from Fig.3 that the macroscopic responses (sub-ballast stress distribution and dynamic stiffness of ballast bed) in DEM modelling are close to those in laboratory test.This validates the DEM model shown in Fig.2.

In the following, the validated DEM model is adopted to obtain multiscale responses of ballast bed under movingcyclic load and train load.The cyclic load applied in DEM modelling is identical to that in the laboratory test [27, 29],given by

Table 1 DEM parameters of ballast particles in numerical model

wherePdis the applied cyclic load,Pampis the loading amplitude,P0is to simulate the static seating force in laboratory, andfis loading frequency.Here we havePamp= 24 kN andP0= 6 kN.

The train load applied in DEM modelling is formulated by series concerning train speed and length [31], given by

wherePaxleis the axle load,αis the spacing between adjacent sleepers,βis the stiffness ratio between rail and sub-rail base,xiis the horizontal distance between wheeliand the rail seat,Lis the length of carriage,tis loading time shown in Fig.4,vis train speed, and <λ> is the integer component ofλ.Here, we haveP0= 6 kN,Paxle= 140 kN,α= 0.6,β= 1.18,L= 25 m,i= 1-4,x1-x4are -5.0, -2.5, 2.5 and 5.0,respectively (i.e., the target sleeper locates in the middle of two carriages), andv= 250 km/h.

The loading frequency of the cyclic load is usually estimated from the train speed byf=kv/L, wherekis the loading cycles per carriage.Since a carriage usually has two bogies,we havek= 2 (with the assumption of even bogie spacing) to simulate the dynamic effect from train load [12].Then, the loading frequencyfin Eq.(1) is calculated as 5.5 Hz.The applied loading curves are shown in Fig.4.It is observed that the cyclic load and train load have the same magnitude.

Generally, applying measured dynamic loads or a numerical load simulated from the train-track dynamic interaction matches the real condition better [12, 32].Since the train load calculated by Eqs.(2)-(3) differs a lot from the cyclic load, as shown in Fig.4, it is qualified to be used in investigating the influence of load pattern on multiscale responses of ballast bed.

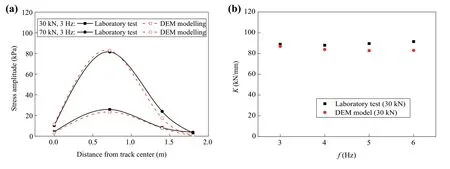
Fig.3 Comparison of the dynamic responses of ballast bed in numerical and laboratory tests: a stress distribution beneath ballast bed; b dynamic stiffness K of ballast bed

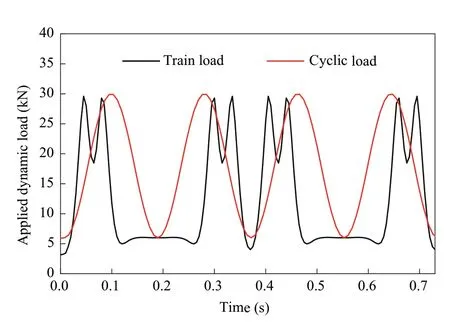
Fig.4 The simulated train load applied in DEM modelling

Before applying dynamic load, the ballast bed model (see Fig.2) has reached the initial equilibrium state.After then,the two loading waves are applied on sleeper to start the loading procedure.In other words, the two numerical tests are exactly the same before loading.The following analysis characterizes the loading-induced variation of multiscale responses.Since the DEM model has more than 11,000 ballast particles, 22 loading cycles are applied within 4 s to obtain a reasonable computation efficiency.There are many macro-scale indicators to characterize the mechanical behaviors of ballast bed, such as the elastic vertical deformation,permanent vertical deformation, stress distribution, stiff-ness, and lateral confinement loss.Since only 22 loading cycles are applied in DEM modelling, indicators having insignificant variation with loading cycles are analyzed,including sub-ballast stress and ballast bed stiffness.

Fig.5 Five sub-regions in ballast bed along lateral direction

3 Quantification of particle-scale characteristics

Experimental studies show that the dynamic load from sleeper follows a diffusion angle of 35° in ballast bed [19,29].Since the thickness of ballast bed beneath the sleeper is 0.35 m, five typical sub-regions with side length of 35 cm in ballast bed along lateral direction are enough to cover the core region, as shown in Fig.5.The 5 regions include three sub-rail regions (R1,R2andR3), a sleeper-end region(R4), and a shoulder region (R5).For each region, multiscale responses are characterized.Meanwhile, in order to emphasize the influence of dynamic load on ballast behavior, the dynamic component of each response is characterized.

In this section, quantifications of micro-scale indicators adopted in this work are introduced.The specific results are analyzed and interpreted in Sect.4.Such arrangement of content helps to compare the inconsistent variation of different indicators simultaneously.

3.1 Particle acceleration

The translational acceleration of the probe particle 10 cm beneath the sleeper end is taken as examples to show the determination of particle acceleration amplitude (Ai,j).Particle acceleration and rotation movements become stable after the initial 6 loading cycles.Figure 6 shows the variation of particle acceleration with loading time during the stable phase, where the direction of rotation motion conforms to the right-hand rule.It is observed that particle acceleration has the same or similar waveform under the applied load after initial several loading cycles.It is observed from Fig.6 that for both cyclic and train load:axandayare close, which are smaller thanaz.This indicates that the unbalanced force is mainly inzdirection, i.e., the loading direction.For a loading cycle, the amplitude of acceleration is characterized as the difference between the maximum and minimum values, as highlighted in Fig.6.Here, ‘a loading cycle’ for train load is taken as the effect from a bogie.

Since a single particle’s acceleration may not be representative, the regional mean amplitude of particles’ translational accelerations is adopted to evaluate the motion intensity of each region.For a sub-rangeRi, the mean amplitude of particles’ translational acceleration is calculated by Eq.(4):

whereiis the sub-range ID,jis the particle ID inRi;NPiis the quantity of ballast particles inRi;Ai,jrefers to the amplitude of the translational acceleration on particlejduring a loading cycle;describes the mean acceleration level inRi.

3.2 Contact network

Contact network is generally defined to describe the internal structure of granular material.There are many quantifications to describe contact network, such as the directional distribution of contact normal and contact force [33, 34, 35], statistical analysis of branch vector [36], coordinate number, and fabric tensor [37].In this study, the coordinate number, contact normal and contact force are adopted to characterize contact network, where contact normal (force) refers to the normal contact vector (force) at each contact.The mean coordinate number of each region is defined in Eq.(5), which describes the contact efficiency inRi; the regional mean contact force is defined in Eq.(6), which evaluates the contact force level inRi.

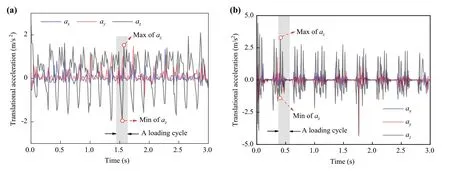
Fig.6 Translational acceleration of the probe particle 10 cm beneath the sleeper end: a under cyclic load; b under train load.ax, ay, and az are the translational accelerations in the x-, y-, and z- directions, respectively

Despite the mean contact force or coordinate number,directional distribution of contact normal is also an important aspect to understand the performance of contact network.For 3D particle assembly, the directional distribution of contact force is usually described by probability density shown in a spherical histogram.However, due to the small quantity of ballast particles in each sub-region, the 3D directional distribution of contact force shows great difference among directions even a large interval of steradian is adopted [4].Considering that the ballast bed is a periodic structure in the longitudinal direction, the contact forces are projected on thex-zplane to mainly analyze the directional distribution of contact force in vertical and lateral directions.The probability of contact normal oriented in the angle interval [θ1,θ2] is expressed byPc(θ), as defined in Eq.(7) [33].Meanwhile, the directional probability distribution of contact normal is weighted by force intensity to better consider load propagation, seePf(θ) defined in Eq.(8).

whereN(θ-Δθ∕2,θ+Δθ∕2) is the number of contact normal oriented in the interval [θ-Δθ∕2,θ+Δθ∕2] , andF(θ-Δθ∕2,θ+Δθ∕2) is the arithmetic sum of forces oriented in the interval [θ-Δθ∕2,θ+Δθ∕2].In the following analysis, Δθis selected as 10º.

WithPc(θ) andPf(θ), the probability density function(PDF) describing the directional distribution of contact normal or contact force is calculated by derivation [33], which is generally given by

whereicould be ‘c’ or ‘f’ to describe the distribution of contact normal or contact force, respectively,θiis the major direction of the probability density distribution, andδiis the deviator of the probability density distribution.Largerδiindicates a more anisotropic distribution ofpi(θ).Figure 8a and b shows the PDF of contact force ofR3at a moment during cyclic loading and train load, respectively.It is observed that the directional probability density distributions of contact force for two loading patterns have the same dominant direction (loading direction), which indicates that the contact force among ballast particles mainly locate along the loading direction.

The contact evolution is characterized by the major direction (θi) and deviator (δi).For all five regions, the deflection ofθiinduced by dynamic loading is no higher than 10°,which is even smaller than the statistical angle interval ( Δθ)of the probability density distribution.Hence,θiis not discussed in the following analysis.In other words, the major direction of contact network is deemed the same throughout the loading cycle.Figure 9 shows the variation ofδfunder cyclic load and train load, respectively, which show similar waveforms as that of the applied loads.Then, the difference between the maximum and minimum values ofδfduring a loading cycle is characterized as the amplitude ofδf, denoted asδampf (also highlighted in Fig.9).The same process is used to obtainδampc.

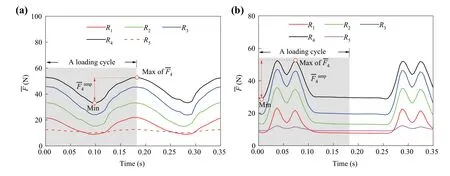
Fig.7 Time history of contact force: a under cyclic load; b under train load

Fig.8 Directional probability density distribution of contact force of R3: a under cyclic load; b under train load

With the above quantifications of particle-scale characteristics and conventional evaluation indicators (sub-ballast stress and dynamic stiffness of ballast bed), the influence of dynamic load waveform on macro- and micro-scale characteristics of ballast bed is quantitatively discussed in the following section.For comparison purpose, all indicators are collected at the same loading cycle.

4 Comparison of multiscale characteristics of ballast bed under cyclic load and train load

The mean particle acceleration under two loading patterns is shown in Fig.10.It is observed that the general variation and distribution of particle acceleration are independent from loading pattern.For example, no matter for cyclic or train load, thez-acceleration is larger thanx- andy- accelerations; particle accelerations at sub-rail regions (R2andR3) are much larger than those at other regions, while, quantitatively, the particle acceleration along a direction under cyclic load is lower than that under train load, except thez-acceleration atR2andR3(which are close).

Figure 11 shows the comparison of contact state under cyclic and train loads.The coordinate number under cyclic load is larger than that under train load, as shown in Fig.11a.This indicates that more inter-particle contacts form to resist the increase in cyclic load.Owing to the same magnitude of two load patterns, the amplitude of contact force under cyclic load should be smaller.In fact, the amplitude of contact force under cyclic load is indeed smaller than that under train load, as shown in Fig.11b.

Figure 12 shows the lateral distribution of the amplitudes ofδcandδfunder two loading patterns, which are close forR1,R2,R4andR5, while, for the sub-rail region(R3),under train load is much larger than that under cyclic load.It is also observed thatis much larger than, indicating that the directional distribution of contact force is more anisotropic than contact normal.In other words, not only more inter-particle contacts form along vertical direction under vertical load, but also the mean normal force on these contacts is considerably larger than the mean normal force on other contacts.This reflects how granular materials self-organize to resist the vertically applied load.

For a regionRi, the sub-ballast stress is calculated as the ratio of the overall contact force on bottom wall within the range ofRito that on the bottom area ofRi, where the bottom area refers to the product of the width ofRi(0.35 m) and the thickness of model box (0.6 m).Figure 13 shows the comparison of the amplitudes of sub-ballast stresses under cyclic and train loads, which are very close in both variation tendency and magnitude.Besides, the dynamic stiffness (K) of ballast bed is also calculated following the method in [15].Then, we haveK= 81 MN/m andK= 87 MN/m for cyclic and train load, respectively.This indicates the equivalent cyclic load performs well in simulating train load from the perspective of macroscopic responses.

Since the above multiscale responses of ballast bed under cyclic load are different in magnitude from those under train load, the deviation is defined as

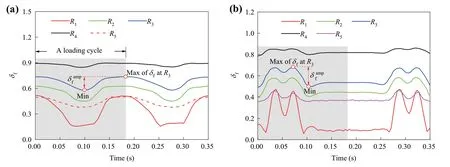
Fig.9 Time history of the anisotropy deviators of contact force: a under cyclic load; b under train load

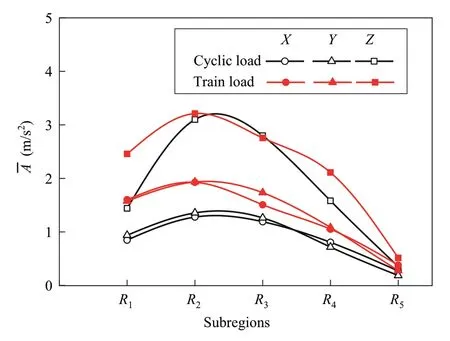
Fig.10 Comparison of lateral distribution of particle acceleration under cyclic and train loads

whereηi(χ) is the deviation ofχatRi;χrefers to any indicator describing the dynamic response of ballast bed, here including particle acceleration, mean contact force, coordinate number, anisotropy of contact network, stress amplitude and track stiffness;refers to theχobtained atRiunder cyclic loading, andrefers to theχobtained atRiunder train load.The positive value ofη(χ) indicates that using equivalent cyclic load tends to overestimate the real intensity ofχ, while the negative value ofη(χ) indicates that using equivalent cyclic load tends to underestimate the real intensity ofχ.

Then for each indicator, the deviation is calculated and shown in Fig.14.It is observed that the deviation of each indicator varies by region.Meanwhile, the maximum deviation of each indicator occurs at different regions.For macroscopic responses (σzandK), the deviations are below 6%.This indicates that using cyclic load to simulate train load is appropriate in obtaining ballast bed deformation and regional stress, while, for particle-scale responses, the absolute values of deviations are much larger.The maximum deviation of, andare about 19.5% (R3), 44.7% (R2), 47.1% (AxatR1), 39.7% (R5), and 24.1% (R5), respectively.This evidences that the similar macroscopic responses (σzandK) result from quite different micro-mechanical process.Particle motion and inter-particle contact force has significant influence on abrasion and breakage of ballast particles.Contact force between particles at shoulder region (R5) are important to lateral confinement and stability of ballast bed.Therefore, the deviations of particle-scale responses under cyclic loading and train load are worth paying attention.

It is concluded from Fig.14 that compared with macroscopic responses, particle-scale responses are more sensitive to the variation of loading type.The inconsistency of multiscale responses to the variation of loading pattern means that the application scale of DEM model should not exceed the validation scale when involving load simplification.Otherwise, it is important to examine multiscale responses to validate the effectiveness of load simplification.

It should be noted that the deviations shown in Fig.14 are obtained from the numerical test model shown in Fig.1.For DEM simulations with different individual features, such as model setup, ballast shape, particle parameters, and loading conditions, the deviation of multiscale responses induced by load waveform variation could be different from Fig.14.

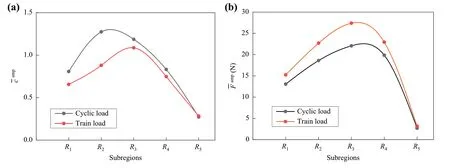
Fig.11 Comparison of lateral distribution of contact state under cyclic and train loads: a coordinate number; b average contact stress

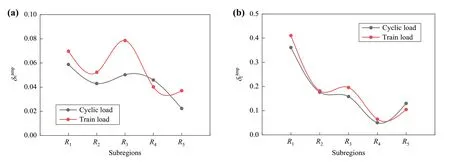
Fig.12 Comparison of lateral distribution of the anisotropy deviators of contact network under cyclic and train loads: a amplitude of δc; b amplitude of δf

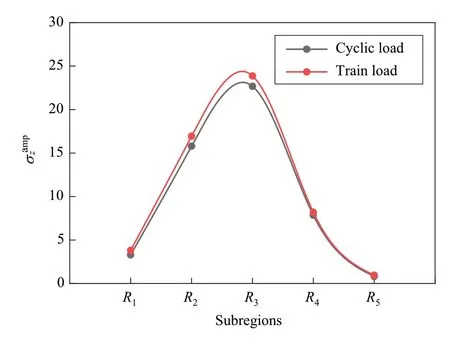
Fig.13 Comparison of lateral distribution of sub-ballast stress under cyclic and train loads

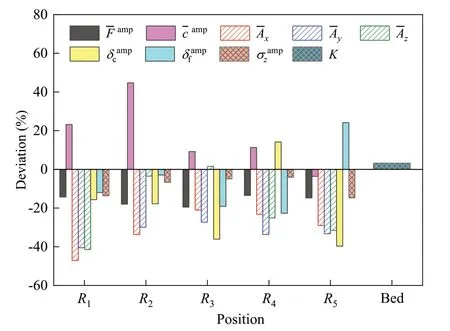
Fig.14 Deviation of multiscale indicators between cyclic and train loads

At least two possible reasons account for this inconsistency of multiscale responses to the variation of loading pattern: (1) The two loading waveforms have different impulse effects, which lead to inconsistent effect on multiscale responses.In this case, the above results obtained from DEM modelling just show the inconsistency.This indicates that the equivalent cyclic load of train load performs well in a specific scale (macro- or micro-scale).(2) This inconsistency may lie only in DEM modelling; e.g., DEM modelling under two loading patterns has accumulated difference during force-displacement iteration.Experimental study of particle-scale characteristics under two loading patterns is expected to illustrate whether the inconsistency exists only in numerical simulation.Before targeting reasons for the inconsistency of multiscale responses induced by load simplifications, it is necessary to pay some attentions to the influence of such inconsistency on characterization of multiscale dynamic responses of a granular system.

5 Conclusions

In this numerical study, we have examined the consistency of multiscale responses under train load and the corresponding equivalent cyclic load.For cyclic load and train load with the same magnitude and amplitude, the induced multiscale responses of ballast bed are different not only in variation pattern but also in magnitude.The maximum difference of macroscopic responses under cyclic load and train load is within 6%, while the maximum difference of particle movements under the two loading patterns reaches up to about 47.1%.This indicates an inconsistent effect of dynamic load waveform on macro- and micro-scale responses: compared with macroscopic responses, particle-scale responses are more sensitive to the variation of loading type.However,the reason for this inconsistency is not fully identified yet,which could be more than the difference of load pattern.Since ballast bed is a discrete system with relative small critical length, it is important to keep the conditions adopted in DEM model the same as the practical conditions of a ballast bed.When simplification (not only loading waveform)is involved in DEM modelling, it is suggested to examine the multiscale responses in various conditions to recognize the potential scope where such simplification performs well;or at least the application scale of DEM model should not exceed the validation scale.

Acknowledgements This work was supported by the NSFS (Natural Science Foundation of Shanghai) Program under grant number 21ZR1465400.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made.The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visit http:// creat iveco mmons.org/ licen ses/ by/4.0/.