卫星星座分布概率解析算法及精度分析

刘慧梁,孙茜,楚尧,彭菲,江帆,吕红剑,蔡亚星,王平

1.中国空间技术研究院 通信与导航卫星总体部,北京 100094 2.国家航天局 卫星通信系统创新中心,北京 100094 3.启元实验室,北京 100095

1 引言

近50年来,人类探索太空的历史先后经历了两次低轨卫星星座的浪潮。20世纪90年代,以“铱星”“全球星”为代表的第一代低轨星座系统旨在提供全球覆盖的通信服务,其星座规模在数十颗卫星量级,提供窄带通信服务,有效补充了地面蜂窝网络未覆盖地区的通信服务空白,特别是为南北极地区,提供了高效、便捷的通信服务[1]。但由于终端成本及业务运营等问题,上述卫星通信公司先后都经历了破产重组,低轨卫星星座系统的第一次发展浪潮也随之陷入低谷。2015年,在谷歌等互联网巨头的推动和支持下,以OneWeb和Starlink为代表的低轨星座在短期内迅速聚集人气,掀起了低轨卫星星座开发的第二波浪潮。与第一代低轨星座系统相比,第二代低轨卫星星座规模有了大幅提升,多数是由数千颗甚至上万颗卫星组成的大型星座,主要提供宽带互联网接入服务[2-4]。

伴随着国外大型低轨星座的快速部署,近地轨道将面临多系统共存的局面[5],为了避免频率轨道资源干扰冲突等诸多问题,通常在星座设计阶段会对在轨及规划的星座进行分析,根据星座特征参数构建分析模型,其中,星座系统卫星位置分布概率的预测及其准确度直接影响着卫星互联网星座系统的运行策略规划[6-7]、通信协议设计[8-9]以及频率干扰分析[10-11]等系统级设计验证工作。高效、准确地实现多系统间卫星位置分布概率提取,是高质量完成系统设计的基础,具体分析方法可以分为基于轨道外推的时域统计法以及基于位置概率的解析算法。

基于轨道外推法的时域统计法通过考虑卫星的各种摄动模型,建立相应的轨道方程,精度高,但计算复杂度大,对于目前动辄万颗卫星规模的大型低轨星座来说,时域统计法计算耗时长、对服务器算力要求高,无法进一步支持对星座系统覆盖率、通信协议、星座频率干扰等开展分析[12-14]。

为弥补上述时域统计方法的不足,提高星座分布概率预测的效率,国际电联先后研究并颁布了S.1529建议书“非静止轨道(non-geostationary orbit,NGSO)卫星固定业务系统和其他卫星系统间干扰统计测定的分析方法”[15],S.1257建议书“从地球表面看NGSO卫星的可见度及干扰数据的计算分析方法”[16],给出了一种基于位置概率的计算方法。通过对典型场景的验证,基于位置概率的计算方法与时域统计方法的结果基本一致,计算时间大幅降低[13,17]。然而,国际电联相关研究在验证基于位置概率的计算结果时,所用时域统计仿真结果包含大量假设前提,例如不考虑地球自转的影响(即假设地球自转角速度为0),设定升交点漂移为固定值(0.06°每公转周期)等,与现实场景之间存在较大差距。此外,两份建议书只对特定场景的概率计算结果与时域统计法进行了数值对比,并未对计算精度及误差产生的原因做系统分析,所提方法对由数千颗卫星构成的大型星座的适用性也没有验证。

本文参考国际电联前期所开展的基于卫星星座位置概率的研究基础,首次提出并详细推导了具有普适性的卫星星座概率分布的解析表达式,引入了地面站可视空域小区内卫星期望值变量,系统验证了对于不同构型大型星座的适用性,通过与时域统计法结果对比,详细分析了地面站在不同纬度下面对单一构型星座场景及混合构型星座场景的计算精度,为精确解析大型卫星星座分布概率提供了理论基础及高效计算方法。

2 解析法公式推导

在卫星系统间频率干扰分析中,利用卫星分布概率确定星座空间位置关系,模拟干扰概率分布曲线,是完成星座系统性能优化及干扰规避策略设计一种重要方法[13]。本节将详细推导解析法求解不同构型星座卫星在可视空域小区中的分布特征,首先求解卫星星座概率密度函数,之后在此基础上推导地面站可视空域小区内卫星期望值。

图1为卫星地面站可视空域划分示意图。将任意地面站可视空域划为更小的小区单元,以正六边形为网格划分,小区单元紧密排列,各区域中心呈三角形排布,方位角0°表示正北方向,90°表示正东方向,180°表示正南方向,极轴长度表示仰角范围,坐标中心点表示地面站正上方,即仰角为90°。

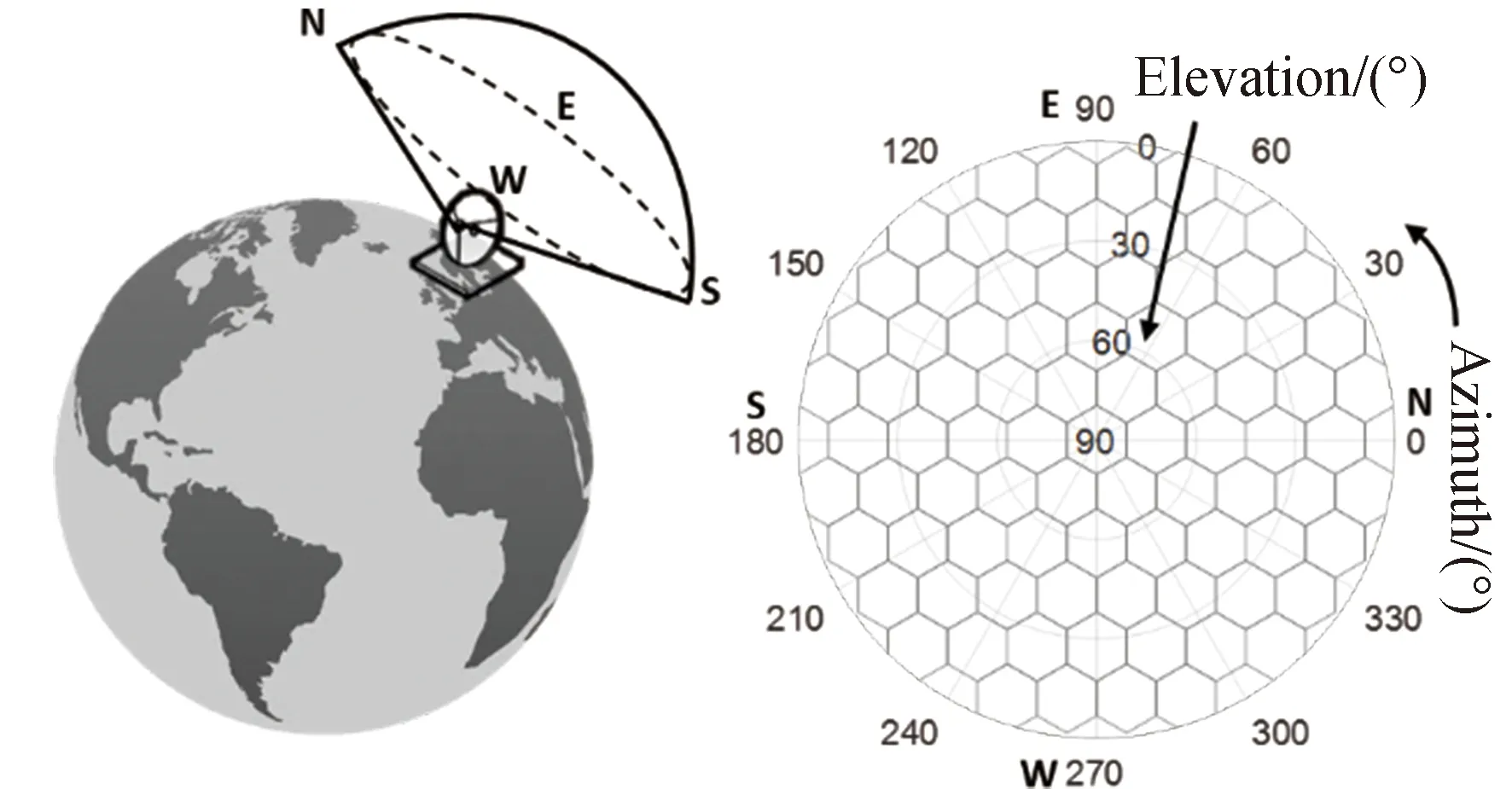
图1 卫星地面站可视空域划分示意Fig.1 Schematic of the Field of View(FOV) division of the satellite earth terminal

2.1 卫星星座概率密度函数

假设某卫星运行在轨道半径为R、倾角为δ的圆形轨道上,若卫星轨道为非回归轨道,则卫星轨迹将逐步遍历半径为R的截断球面,形成轨道壳,如图2所示。

图2 非静止轨道卫星轨道壳示意Fig.2 Schematic of the orbit shell for NGSO (non-geostationary orbit)satellite

该轨道壳上的卫星位置可用星下点经度ψ和纬度φ表示,由于围绕地球极轴的自转具有对称性,所以卫星轨道壳的经度将均匀分布,但是,卫星所处纬度的概率,与其运行轨道倾角相关。运行于圆轨道的卫星位置矢量如下:

式中:τ为服从[0,1]均匀分布的随机变量;z为卫星位置矢量在地心指向北极方向上的分量。

即

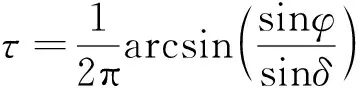
(1)

式(1)存在两个解,分别对应运行中卫星星下点纬度增大和纬度减小的两种情况,因此卫星位于纬度区间[φ1,φ2]内的概率为:

则卫星在纬度方向的概率密度为:

由于卫星在轨道壳经度方向均匀分布,所以,概率密度函数可表示为:

(2)

图3展示了倾角为45°的圆形轨道面上卫星的概率密度函数,其在南北纬大于45°区域概率密度为0;在小于或等于45°的区域,赤道上空卫星概率密度最低,随纬度增加,概率密度单调递增。

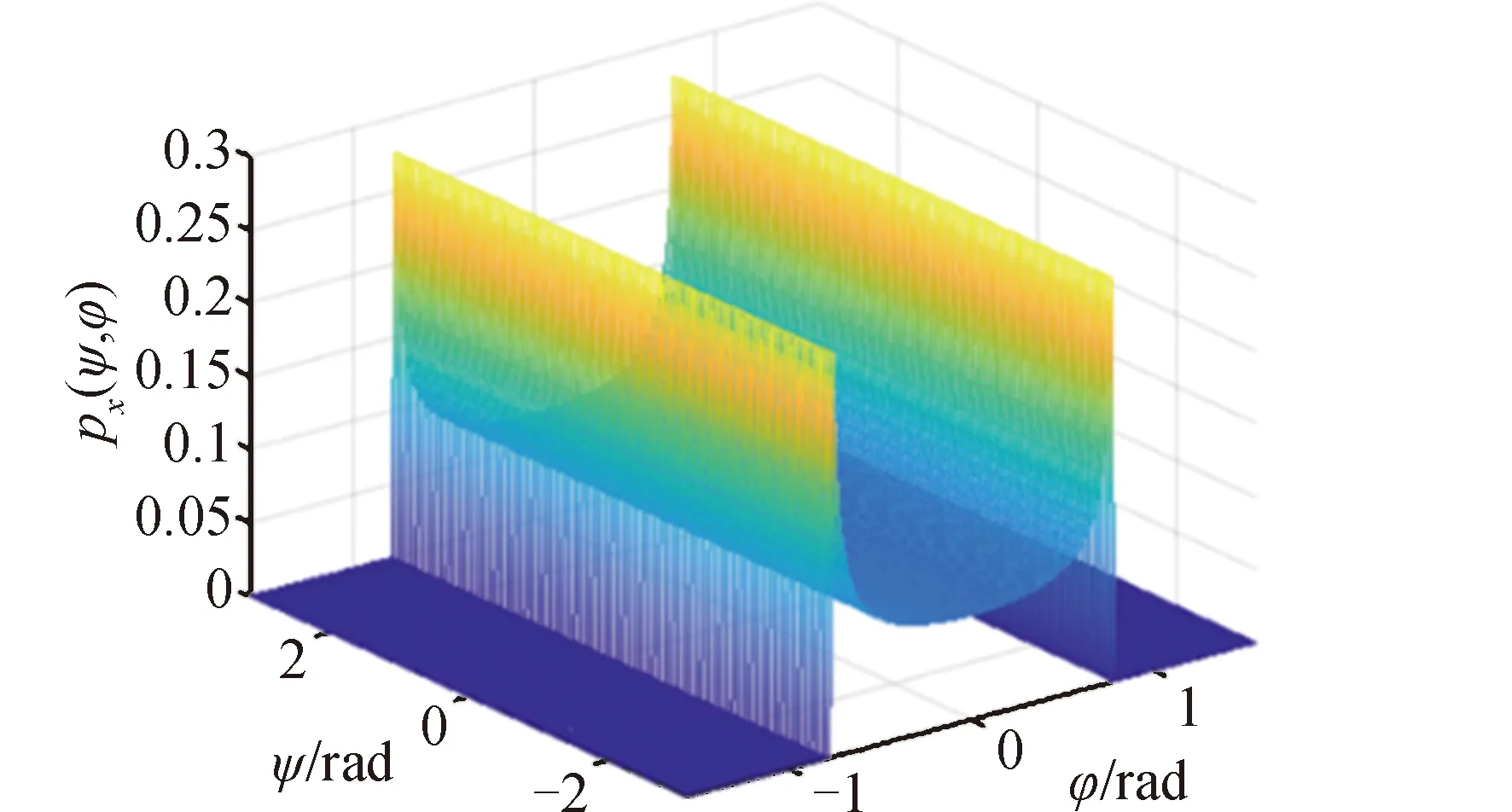
图3 倾角为45°时卫星概率密度函数Fig.3 Probability density function of a satellite placed in a circular orbit plane with the inclination of 45°

2.2 地面站可视空域小区内卫星期望值

地面站T与其可视空域小区Ci的几何关系如图4所示。卫星出现在小区Ci中的概率为

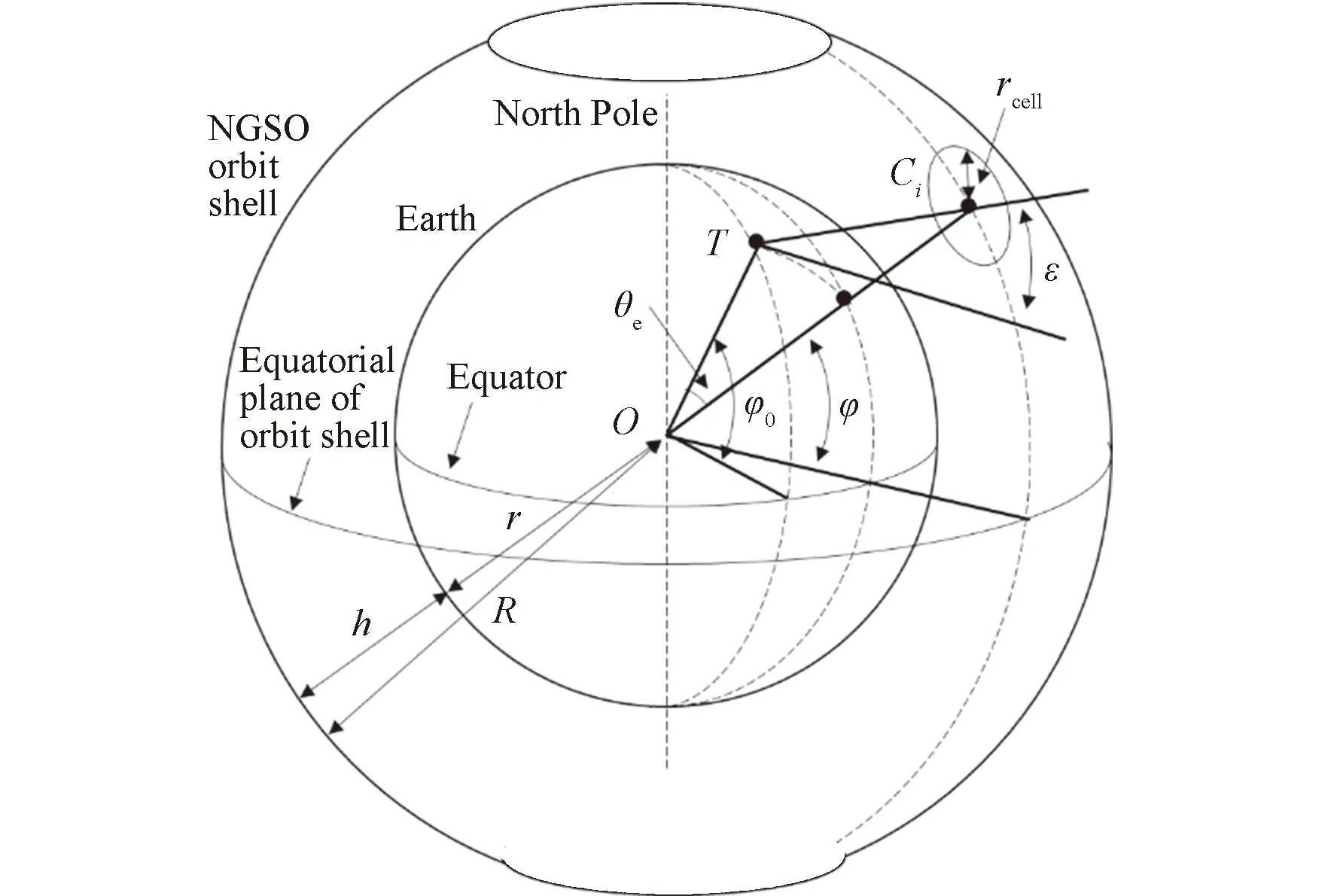
图4 地面站可视空域小区几何关系示意Fig.4 Schematic of geometric relationship for NGSO satellite in the FOV of satellite earth terminal

p=pC(ψ,φ)dS

(3)

即概率密度函数在小区Ci上的面积分。假设概率密度函数在被积分面积上均匀,则有

pi=pC(ψi,φi)AC

(4)

式中:pC(ψi,φi)为小区单元中心点对应的卫星概率密度;AC为地面站可见空域小区单元的球面度(单位sr)。若可视空域小区为圆形,则面积AC的表达式为:

式中:Δθε和Δθβ分别为空域小区Ci的俯仰角差和方位角差所对应的地心角差,可由地面站与可见空域小区的位置几何关系求出,表达式如下:

θε_min=arccos[kcos(ε-rcell)]-(ε-rcell)

θε_max=arccos [kcos(ε+rcell)]-(ε+rcell)

Δθε=θε_max-θε_min

式中:r与R分别为地球半径和卫星圆轨道半径,ε和θε分别为空域小区中心点对应的地面站仰角与地心角,θε_min与θε_max分别为空域小区上边缘与下边缘对应的地心角,rcell为可视空域圆形小区半径。

当卫星总数为N时,对某一确定地面站,其可视空域小区Ci内,卫星期望值为:

E=Npi=NpC(ψi,φi)AC

(5)

当卫星星座存在k种不同构型时,对某一确定地面站,其可视空域小区Ci内,卫星期望值为:

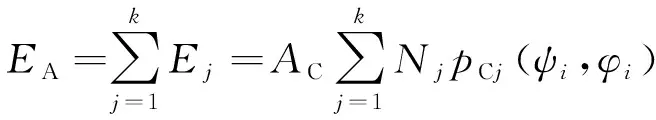
(6)

3 不同构型星座计算结果及精度分析

本节将利用以上推导的解析法公式,求解不同构型星座对于地面站可视空域小区卫星出现期望值的计算结果,并对计算精度进行分析。本文选取两个典型的Walker星座构型作为研究对象,分别研究单一构型及混合构型条件下的分析结果,具体构型轨道参数见表1。其中,构型A为δ型Walker星座,包括3200颗卫星,轨道高度1150km,倾角为60°;构型B为星型Walker星座,包括2880颗卫星,轨道高度1200km,倾角为88°。

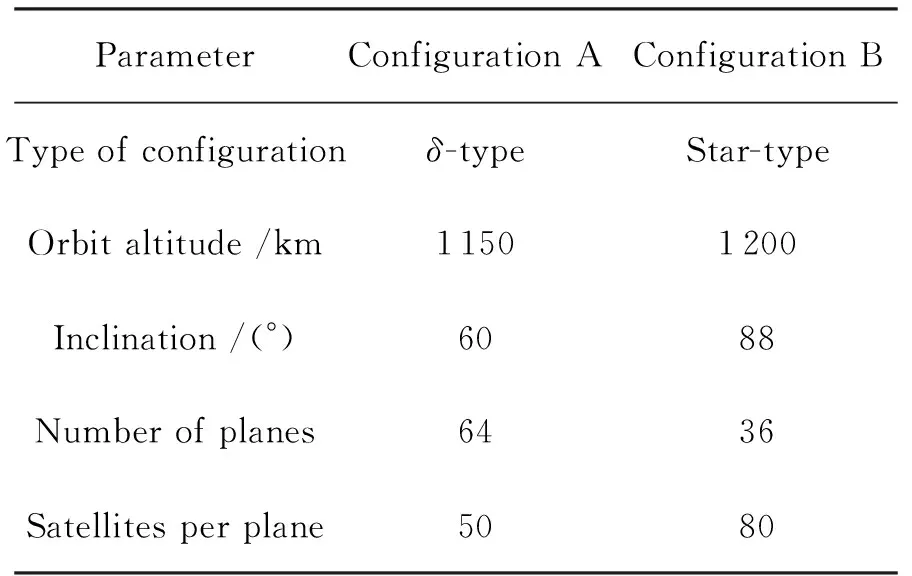
表1 非静止轨道通信星座轨道参数Table 1 Orbit parameters of NGSO satellite systems

在验证计算精度时,采用基于轨道外推的时域统计结果ES与基于位置概率的解析法计算结果EA的比值作为评估指标,其中基于轨道外推的时域统计结果采用圆轨道,仿真步长为10s,总仿真时长为10000h(约417d),即以年为星座运行时长量级评估解析算法计算精度。在地面站空域划分中,本文选取可视空域小区中心点仰角大于20°区域范围进行统计及计算,可视空域小区半径rcell最大选取10°,最小选取2°。图5(a)展示了可视空域小区半径为10°时,仰角大于20°区域范围被划分61个小区单元,图5(b)展示了可视空域小区半径为4°时,相同区域范围被划分367个小区单元。小区单元紧密排列,各区域中心呈三角形排布,极坐标中,极轴长度表示仰角范围,坐标中心点表示地面站正上方,即仰角为90°,方位角0°表示正北方向,90°表示正东方向,180°表示正南方向。

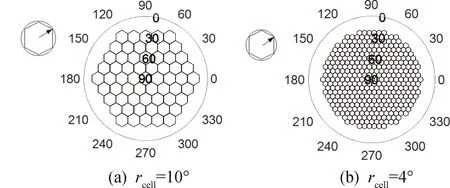
图5 地面站可视空域小区单元划分Fig.5 Schematic of the FOV division of the satellite earth terminal

3.1 单一构型星座计算结果及精度分析

首先,对单一构型星座卫星位置概率计算结果进行分析。构型A星座在不同纬度地面站可视空域卫星期望值由式(5)计算,具体期望值分布如图6所示。结果中圆圈位置表示子空域中心,灰度图例表示卫星出现在小区单元的期望值,方位角0°表示正北方向,极轴长度表示仰角范围。当地面站位于0°(N)时,正上方空域(仰角等于90°)小区单元内卫星期望值最小,随着仰角降低,四周小区单元卫星期望值逐渐增加,由于构型A星座包含卫星数量高达3200颗,所以在视场边缘小区半径为10°区域(正北、正南方向)卫星期望值可达3.2。当地面站位于30°(N)时,随着地面站纬度增加,图中北方的卫星出现概率会略高于南方。当地面站位于60°(N)时,卫星集中于可视范围内南方区域,北方大部分区域卫星期望值为0,对应式(2)中卫星星下点纬度大于卫星轨道倾角的区域概率密度为0。

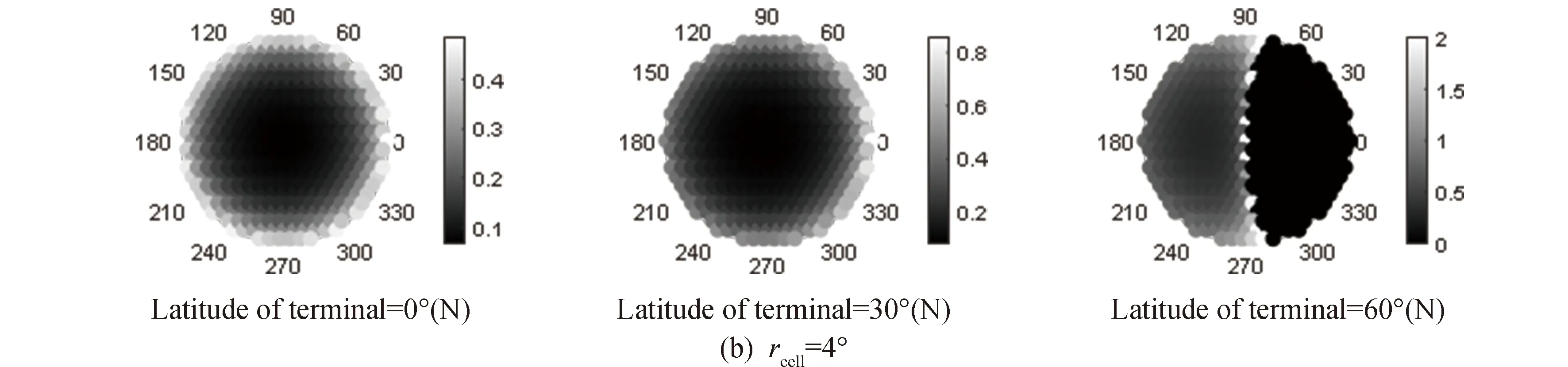
图6 构型A星座地面站可视空域小区卫星期望值Fig.6 Expectation of satellite in the FOV of satellite earth terminal for the constellation with configuration A

图7展示了采用基于轨道外推的时域统计小区单元内卫星期望值ES与基于位置概率的解析法计算卫星期望值EA的比值,可以看出,小区单元半径越小,则期望值比值越接近于1,即基于轨道外推的时域统计结果与基于卫星位置概率的解析算法越接近。从理论上讲,即小区单元面积越小,基于式(4)的近似算法与式(3)的概率密度面积分结果越吻合。地面站纬度小于或等于45°时,基于位置概率的解析算法与基于轨道外推的时域统计结果相比,误差最小为0.1%(小区半径为2°时),误差最大为3.1%(小区半径为10°时)。当地面站纬度等于卫星轨道倾角,即60°时,由于卫星轨迹覆盖边缘存在未占满小区单元,总体误差平均值有所增加,为4.1%至6.7%。

图7 构型A星座地面可视空域卫星期望值基于轨道外推法计算结果ES与解析法计算结果EA比值Fig.7 Ratio of expectation by simulation and expectation by analytical method for constellation with configuration A

构型B星座在不同纬度地面站可视空域卫星期望值同样由式(5)计算,具体期望值分布如图8所示。当地面站位于0°(N)时,正上方空域卫星出现概率最低,随着仰角降低,四周小区单元内卫星出现概率逐渐增加,构型B星座包含卫星数量为2880颗,略小于构型A星座,视场边缘小区半径为10°区域(正北、正南方向)卫星期望值最大为2.6。当地面站位于30°(N)时可明显看出,随着地面站纬度增加,图中北方的卫星期望值会逐渐高于南方。由于构型B星座倾角为88°,空间分布特征和之前所述构型A星座表现出一定差异,其在高纬度地区仍有较好的可见性,当地面站位于60°(N)时,正北方向可视空域边缘小区半径为10°区域卫星期望值可达到12.2。

图8 构型B星座地面站可视空域小区卫星期望值Fig.8 Expectation of satellite in the FOV of satellite earth terminal for the constellation with configuration B

图9展示了构型B星座采用基于轨道外推的时域统计小区单元内卫星期望值ES与基于位置概率的解析法计算卫星期望值EA的比值。当地面站纬度为0°(N)和30°(N),误差最小为0.1%(小区半径为2°时),误差最大为2.9%(小区半径为10°时)。当地面站纬度为60°(N),误差最小为0.05%(小区半径为2°时),误差最大为2.6%(小区半径为10°时)。

图9 构型B星座地面可视空域卫星期望值基于轨道外推法计算结果ES与解析法计算结果EA比值Fig.9 Ratio of expectation by simulation and expectation by analytical method for constellation with configuration B

3.2 混合构型星座解析精度分析

在对单一构型星座卫星位置概率计算结果

进行分析的基础上,本小节将针对包含构型A及构型B的混合构型星座,展示由式(6)计算的不同纬度地面站可视空域卫星期望值,并对计算精度进行分析。

混合构型星座期望值分布如图10所示。由于该混合构型星座为构型A星座与构型B星座叠加,所以图10地面站可视空域小区卫星期望值为图6与图8结果叠加。当地面站位于0°(N)时,正上方空域(仰角等于90°)小区单元内卫星期望值最小,随着仰角降低,四周小区单元卫星期望值逐渐增加,在视场边缘小区半径为10°区域(正北、正南方向)卫星期望值为5.8。当地面站位于30°(N)时,图中北方的卫星出现概率会略高于南方。当地面站位于60°(N)时,卫星期望值分布包括构型A特征,即卫星分布集中于可视范围内南方区域,又包括构型B特征,正北方向可视空域边缘小区半径为10°区域卫星期望值可达到12.2。

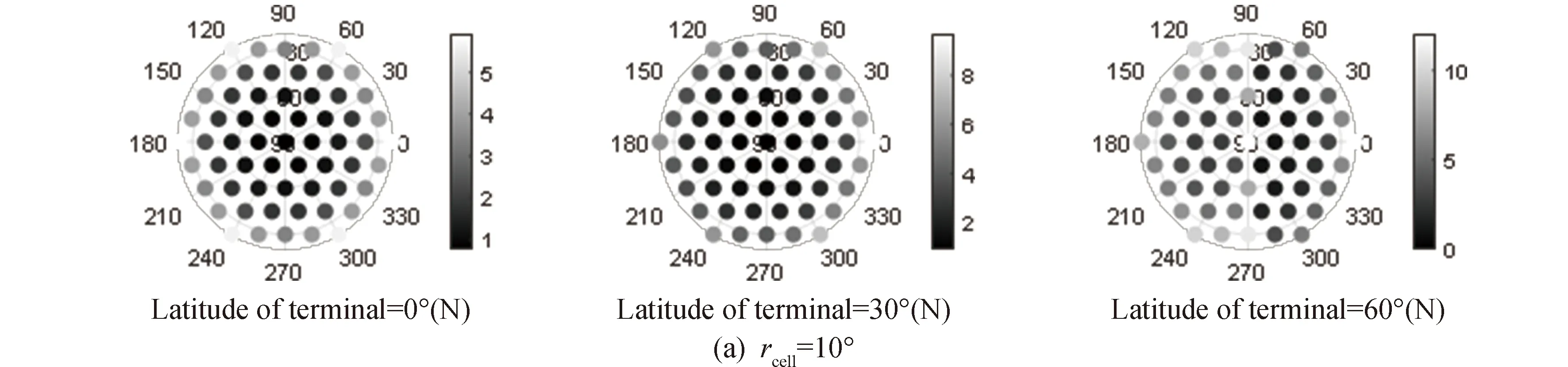
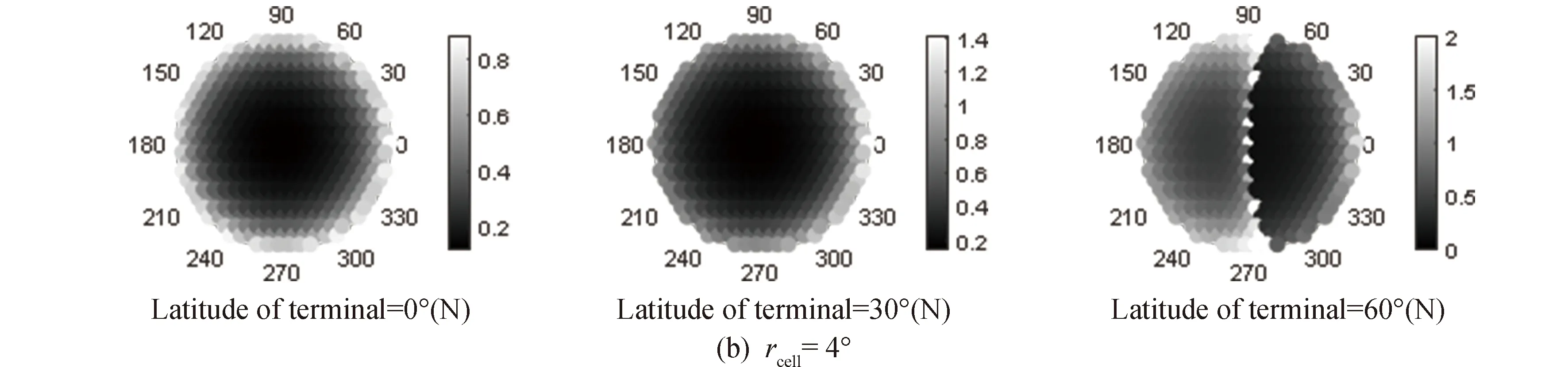
图10 混合构型星座地面站可视空域小区卫星期望值Fig.10 Expectation of satellite in the FOV of satellite earth terminal for the constellation with hybrid configuration

图11展示了混合构型星座采用基于轨道外推的时域统计小区单元内卫星期望值ES与基于位置概率的解析法计算卫星期望值EA的比值。当地面站位于0°(N)和30°(N)时,基于位置概率的解析算法误差最小为0.1%(小区半径为2°时),误差最大为2.9%(小区半径为10°时)。当地面站纬度等于构型A卫星轨道倾角,即60°时,总体误差平均值增加为3.5%至5.8%。

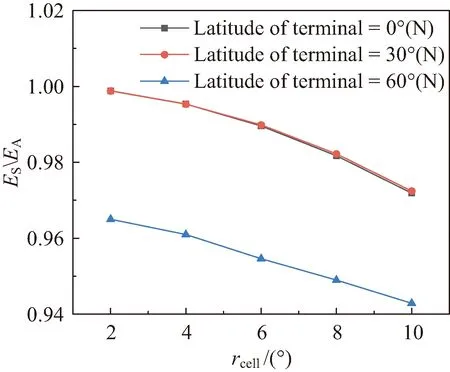
图11 混合构型星座地面可视空域卫星期望值基于轨道外推法计算结果ES与解析法计算结果EA比值Fig.11 Ratio of expectation by simulation and expectation by analytical method for constellation with hybrid configuration

4 结论

为满足日益增长的卫星星座空间分布概率快速分析需求,本文首次提出并详细推导了具有普适性的星座概率分布解析表达式,引入了地面站可视空域小区内卫星期望值变量,并系统验证了所提解析算法对于不同构型大型星座的适用性。与传统基于轨道外推的时域统计法结果相比,期望值解析算法的结果误差大小与可视空域小区单元半径相关,小区单元半径越小,解析算法结果误差越小:当可视空域小区单元半径等于10°时,最大误差为3.1%,当小区半径减少至2°时,最大误差小于0.1%。除此之外,本文还详细分析了地面站部署在不同纬度时对单一构型星座场景及混合构型星座场景的计算精度的影响。当地面站纬度从0°不断增加至星座轨道倾角角度时,卫星轨迹覆盖边缘会逐渐出现未占满小区单元、从而导致计算结果误差增加的情况。利用本文所提解析算法可以快速计算地面站可视空域内特定区域卫星出现期望值,为快速评估卫星星座分布概率、星座系统覆盖性分析及系统间频率干扰分析提供了理论基础及高效计算方法。