数字式太阳敏感器系统精度提升方法及验证
2023-11-18谢任远王北超李爽何益康吴迪孙朔冬
谢任远,王北超,李爽,*,何益康,吴迪,孙朔冬
1.南京航空航天大学 航天学院,南京 211106 2.上海航天控制技术研究所,上海 201109
1 引言
随着小卫星技术的快速发展,微型化、高精度和高可靠性已成为卫星姿态控制的发展趋势[1],这同时要求卫星姿态敏感器具备精度高、低功耗和质量轻等特性。寿命长、可靠性高、精度高以及智能自主控制部件的模块化和微型化已成为未来卫星姿态控制技术的发展方向[2]。太阳敏感器是卫星姿态控制系统的关键组件,是航天领域中应用最广泛的一类敏感器[3],它能够获取太阳在航天器坐标系中的方位信息。姿态敏感器常选用太阳等恒星作为定位参考。太阳的亮度较高且均匀,离地球也更近,这类姿态敏感器具备高精度、轻重量和低功耗特性。
目前,太阳敏感器主要包括0-1式、模拟式和数字式等[4]。0-1式太阳敏感器用于太阳捕获、判断卫星进入地影区以及安全模式。模拟式太阳敏感器能够测量特定视场中太阳矢量相对于敏感器坐标系的方位,其精度一般在1°以内[6-8]。这类敏感器结构简单、体积小、功耗低,虽然测量精度较低,但能满足微小卫星的应用需求。
随着卫星应用需求的不断增长,由于模拟式太阳敏感器很难再进一步提升分辨率和测量精度,因此数字式太阳敏感器应运而生。早期的数字敏感器主要为码盘式,即使用光学码盘完成太阳光入射角的数字化编码,但码盘与电池片、处理电路与探测器的联结工艺限制了码盘式敏感器的应用[10]。随后,研究者们开发了线阵式太阳敏感器,单一基片上的多个光电二极管阵列能够集成动态移位寄存器。该敏感器结构简单,但灵敏度低且噪声大[11]。有源像素结构(active pixel structure,APS)是目前主流的高精度数字式太阳敏感器,通常采用CCD或CMOS作为探测器[12]。CCD图像传感器具备了高集成度、超低噪声、高动态范围等特性,在大视场中的精度可达0.01°。卫星小型化需求推动了敏感器的微型化,但CCD敏感器的质量和体积大且功耗较高[13]。相比之下,CMOS传感器在集成度、功耗等方面具有很大优势,更好地满足太阳敏感器的小型化、模块化需求,并具备较强的抗辐射能力,更适用于复杂空间环境[14]。
太阳敏感器旨在获取卫星自身的姿态信息,保证敏感器的高精度和高可靠性是空间任务顺利完成的前提。数字式太阳敏感器一般会在探测器上安装玻璃层进行保护,并且在玻璃层和探测器之间充惰性气体。由于玻璃层的存在,导致光线进入到探测器前会经过折射,则测量的结果存在误差,而且随着视场角的增大,光线折射会导致误差随之增大,而且该误差与测量角度呈非线性关系,极大影响了太阳敏感器的测量精度[15]。本文开展了数字式太阳敏感器的精度提升研究,并通过实测数据验证了方法的可行性与有效性。
2 太阳敏感器工作原理
数字式太阳敏感器通过测量太阳光线相对于空间飞行器本体轴或坐标平面之间的夹角,并提供给控制系统,从而确定卫星在空间中的姿态[16]。数字式太阳敏感器的工作原理为:太阳光线经数字式太阳敏感器的单孔光学滤光片,成像在图像传感器上形成光斑,太阳光的角度可由太阳光斑于探测器的相对中心位置的偏差计算得出。太阳光线入射从数字太阳敏感器滤光片至图像传感器像面的光路如图1所示。

图1 太阳光线在数字太阳敏感器中的光路Fig.1 Solar ray in digital sun sensor
太阳光进入敏感器后在A点形成光斑,经光斑提取可获得质心坐标X,Y,并利用已知的探测器中心值(X0,Y0)获得相对探测器原点的距离R。
(1)
根据产品标定的焦距h值,可得太阳光入射角α=atan(R/h)。进一步根据光斑坐标(x,y),可获得太阳矢量在探测器的方位角β=atan(y/x)。则太阳矢量在太阳敏感器坐标系中的表达式为:

(2)
随后,图2给出了太阳角度的定义:1)X向太阳角:太阳光线矢量在YbObZb平面上的投影与ObZb轴的夹角,φ=atan(Ssy/Ssz);2)Y向太阳角:太阳光线矢量在XbObZb上的投影与ObZb轴的夹角,θ=atan(-Ssx/Ssz),根据右手法则确定姿态极性。
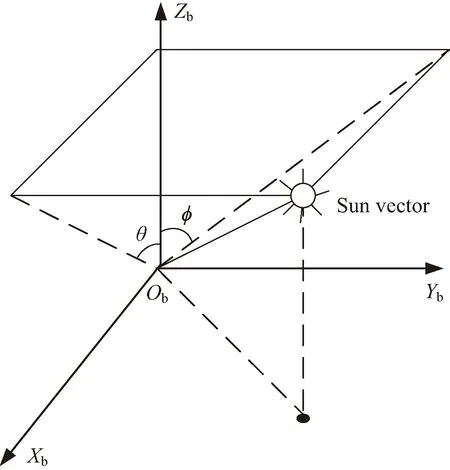
图2 太阳敏感器在本体系中的角度定义Fig.2 Angle definition of sun sensor in this system
3 系统精度提升方法
数字式太阳敏感器的误差主要有:随机误差和系统误差两种。随机误差主要由光学镜头装配精度和探测器噪声引起。虽然随机误差无法彻底消除,但采用相应的手段可对误差进行控制。系统误差则是指用户在使用数字式太阳敏感器中获取角度的误差,主要误差是光学折射造成的。因为探测器表面有保护玻璃盖片,导致光线经过空气与玻璃两种界质传输至探测器时存在折射,使得光斑存在偏离。
针对系统误差,目前主要采用分段二元一次拟合法来校正误差以提高精度。在地面将数字式太阳敏感器放在二维精密转台上,二维转台的输入角度(ξ,η)与敏感器的输出值(Xm,Ym)间的关系可通过测量获得,随后利用二元多次函数拟合测得的原始数据,再进行插值可得(ξXm,ηYm)。然后,系数a、b、c可根据一定的规则分组进行拟合后得到,并根据标定系数和敏感器测量值计算角度,经验证两轴角度可达到0.04°偏差的精度。本文从实际物理特性出发,利用光线传播原理,给出了修正折射影响的非线性角度计算公式,从而获得太阳光的真实入射角度。根据太阳敏感器产品实际的光学系统情况[17],光线至图像传感器的实际像面路径如图3所示。

图3 太阳光线至传感器的实际像面路径Fig.3 Actual image surface path of solar ray to the sensor
经过折射后,在探测器上的成像光斑由A点移至B点,则使用原有计算方式计算的入射角将有较大误差。考虑光线进出滤光片前后的太阳角度不变,且使用了小孔成像方式,因此真实入射角a1与光斑至原点距离的关系可表示为:

(3)
式中:H1表示滤光片下表面到玻璃盖片上表面的距离;H2为玻璃盖片的厚度;H3为玻璃盖片下表面到探测器表面的距离;n1为真空折射率;n2为玻璃盖片折射率;n3为惰性气体折射率。由于惰性气体的折射率很小,因此将n1和n3简化均取为1,则上式简化为:
(4)
该方程为非线性方程,在卫星实际在轨应用中不易求解,故使用牛顿迭代法和弦截法进行求解。
3.1 牛顿迭代法
为求解式(4),构建如下的非线性方程
(H1+H3)tana1-R=0
(5)
式(4)不存在求根公式,求解精确根非常困难。因此,方程的近似根成为求解的重点。牛顿迭代法常用于方程近似根的求解,该方法能平方收敛于方程f(a1)=0的单根附近,已广泛应用于计算机编程中。使用牛顿迭代法求解式(5),解的初值选用a11=atan(R/h),并在此处进行迭代
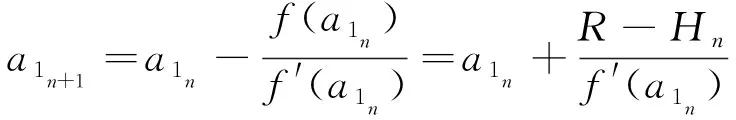
(6)
式中:
f(a1n)的导数为
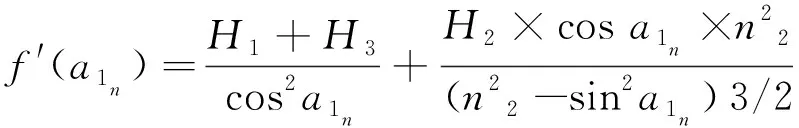
(7)
经过三次迭代后可得到接近真值的入射角。
3.2 弦截法
在牛顿迭代法中,需保证一阶导数存在且不为0。在计算时需求解一阶导数,在星上使用时计算耗时较长。因此,使用差商代替导数的弦截法进行计算。弦截法的原理是以直代曲,即用弦(直线)代替曲线求得方程的近似解。从几何意义上而言,弦截法就是将牛顿迭代法的切线全部用割线替代。对牛顿迭代公式进行如下变形:
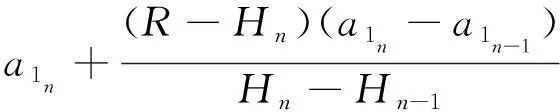
(8)
弦截法在计算时需要用到前两步信息a1n-1和a1n,在首次计算时,直接选用a11=atan(R/h)为计算初值,在第二次计算时需用到a10。根据产品的固有特性,在太阳刚进入敏感器视场时,折射产生的偏差角度在几度的量级,故取a10=a11+0.05(rad)。只用一次弦截法得到近似解误差较大,可能不满足精度要求,要根据第一次弦截法的结果进行多次迭代。后续计算可直接选用前两次迭代计算后的值。
4 实测验证
以某项目的产品参数及实测数据作为验证的输入,产品参数包含了H1、H2、H3、n2、X0、Y0,实测数据包含了光斑的质心坐标X、Y、卫星运行的轨道参数、卫星的姿态以及数字式太阳敏感器的安装矩阵。运行这些参数可以获得理论上的太阳光线在本体系下的矢量。使用太阳敏感器安装矩阵可将敏感器获取的太阳光矢量统一转换到本体系中。
4.1 无修正情况
根据实测数据,获取太阳光从进入敏感器视场到出敏感器视场的一系列质心坐标,通过质心坐标计算获得太阳光矢量,最终获得X向、Y向太阳角。同样地,将获得的理论太阳矢量计算得到X向、Y向太阳角。测量及理论的X向、Y向太阳角的曲线和误差曲线如图4和图5所示。在无修正情况下,X向太阳角的平均误差为3.805°,Y向太阳角的平均误差为4.051°。视场角度与折射率导致的距离误差成正相关,增大视场角度也会导致角度偏差变大。

图4 无修正下X向太阳角及误差Fig.4 X-direction solar angle and error without correction
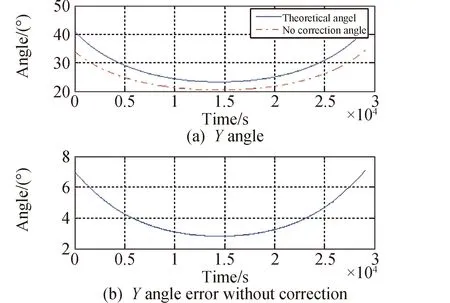
图5 无修正下Y向太阳角及误差Fig.5 Y-direction solar angle and error without correction
4.2 牛顿迭代法修正
根据3.1章节中同样的实测质心坐标数据,通过折射率修正获得修正后的入射角,再根据方位角获得牛顿迭代法修正后X向太阳角、Y向太阳角。牛顿迭代修正后及理论的X向、Y向太阳角的曲线和误差曲线如图6~7所示。在牛顿迭代修正下,X向太阳角的平均误差为0.017°,Y向太阳角的平均误差为0.004°。显然,通过折射率的牛顿迭代修正后,角度精度得到了极大提升。
4.3 弦截法修正
在牛顿迭代法优化的基础上,使用计算简便的弦截法,同时给出设置前两拍数据,计算修正后X向太阳角、Y向太阳角。弦截法迭代修正后及理论的X向、Y向太阳角的曲线和误差曲线如图8~9所示。在弦截迭代修正下,X向太阳角的平均误差为0.017°,Y向太阳角的平均误差为0.004°。使用弦截迭代修正后,角度精度同样得到了极大提升。在迭代次数相同的条件下,简化计算的弦截法与牛顿迭代法的精度一致。
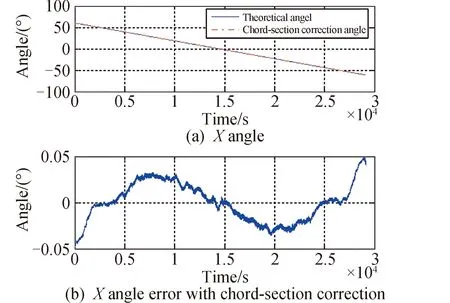
图8 弦截修正下X向太阳角及误差Fig.8 X-direction solar angle and error with secant iteration correction

图9 弦截修正下Y向太阳角及误差Fig.9 Y-direction solar angle and error with secant iteration correction
5 结论
本文以某卫星研制项目为背景,使用数字式太阳敏感器获取卫星姿态角度。通过对系统误差及角度计算原理的详细分析,获得了角度误差公式。提出了修正折射影响的非线性角度计算公式,对非线性方程进行线性化计算处理,分别使用牛顿迭代法和弦截法计算角度。考虑实际在轨应用,给出了星上编程计算的实现方式。最后用产品实测数据进行了仿真验证,两种方法的计算精度相比于无修正情况均提升了约3.94°,相比于多元函数拟合提升了约0.02°,该方法用于精度提升的有效性和星上编程计算的可行性得以验证。最后总结,各种计算方法的总体情况如下:
1)使用无修正方式计算角度最为简单,但精度较差;
2)当迭代次数相同时,牛顿迭代法和弦截法的角度计算精度一致;
3)使用牛顿迭代法时,需要进行微分计算,耗时较大;
4)弦截法计算要用到三拍的数据,变量占用的空间较大。
