基于Markov-ADC模型的星座覆盖性能分析
2023-11-18孙景云张国亭柳震郭洁王进
孙景云,张国亭,柳震,郭洁,王进
1.北京跟踪与通信技术研究所,北京 100094 2.航天科工集团第三研究院 航天科工海鹰卫星运营事业部,北京 100071
1 引言
随着卫星通信、遥感和导航等应用领域对全球覆盖需求的快速增长,大型星座进入蓬勃发展时期,其突出特点表现在:星座规模巨大,任务复杂多样;星座卫星小型化、低成本要求高,在轨出现故障的概率更高。不同于单星系统,星座系统通常需要多颗卫星协同执行跟踪、观测、数传等任务,传统的以单星为目标的性能评估预测以满足星座完成多种复杂任务的需求,为保证星座的安全运行和高效运用,需要以整个星座为对象进行可用性及服务能力的研究与应用。
目前对星座的可用性及服务性能尚无统一定义,评估方法也千差万别。评估可以理解为通过某一种规则途径,在规定背景或场景下,对某个特定系统或体系进行评价,主要的评估方法有ADC方法[1]、模糊综合评判[2]、层次分析法[3]、神经网络[4]等。其中,ADC方法可以综合评估系统可用度、可信度和综合效能,能够较为全面地反映星座系统的可用性、系统状态转移情况以及星座服务能力,故而本文采用该种评估方法作为星座性能指标评估的基本手段和理论工具。
岳健等基于ADC方法对反舰导弹武器系统进行效能评估[5],张天琦等利用ADC方法建立了防空导弹武器装备体系效能评估模型[6],汪慧阳等根据实际任务提出改进的ADC模型实现通信对抗系统作战效能定量评估[7],何胜杰等将ADC法应用于无人机对地攻击任务的效能评估中[8],以上文献研究验证了ADC效能评估模型的有效性。
单星的故障或失效并不一定导致星座运行故障,但可能导致整个星座系统服务性能下降。邵瑞瑞等构建一种基于生灭过程的BDP-ADC(birth-death process-availability,dependability,capacity,生灭过程-可用度、可信度和星座能力)模型用于评估铱星效能[9],文中假设在一个很小的时间区间内有且仅有一颗卫星故障或修复,然而实际应用中存在多颗卫星同时发生故障或瘫痪的情况。杨卓鹏等提出以星座可用性、连续性、覆盖性为构成要素[10],集成应用Petri网、中断分析、贝叶斯网构建导航星座系统效能评估模型。王宇从网络连通度入手,采用生成树相关理论方法计算系统状态转移概率并得到可靠性矩阵,以ADC模型为基础对通信星座进行效能评估[11]。
李国重等利用马尔科夫链等方法建立了单星可用性评估模型并利用组合数学和全概率公式建立了导航星座PDOP(position dilution of precision,位置精度因子)可用性评估模型,文中星座状态间相互独立,并未描述星座状态间相互转移过程[12]。王尔申等基于马尔科夫过程同时考虑卫星故障率和修复率的单星可用性模型[13],并结合卫星备份情况提出了空间信号层和服务层的星座可用性评估方法模型,文中只考虑了相邻星座状态之间的转移情况。侯洪涛等结合基于马尔科夫过程的单星可用度算法和基于星座状态概率的服务可用性模型[14],解决了基于部件失效分析导航星座可用性的近似算法。
综上,上述文献效能评估的研究主要有以下几个方面问题:1)星座状态转换情况比较复杂,已有的评估方法只对星座状态概率进行分析,忽略了星座状态转换情况或对星座转换问题描述不够精细;2)研究对象为通信、导航、遥感卫星或星座中某一类,分析指标多为覆盖区域内法的PDOP值、网络连通度等,缺少通用类指标,难以建立通信、导航、遥感通用型评估体系,由此导致提出的评估方法具有一定的局限性。覆盖性可以反映星座构型情况,是星座提供通信、遥感、导航等各类服务的先决条件。本文从单星平均故障率和修复率出发,利用马尔科夫链方法建立了星座可信性数学模型,选择覆盖重数、重访间隔、平均单日星座-目标连接数、全覆盖所需时长通用性覆盖指标作为能力要素,并对设定的场景以及中国服务区内覆盖性能进行了仿真分析。
2 ADC评估模型
ADC方法将系统性能与系统初始状态、状态转移以及能力指标关联起来,其基本数学模型可以表示为:
E=A·D·C
其中,E:系统效能,表征相应的系统能力指标受可用度和可信度影响后的实际效能值,反映星座的系统效能情况。
A:可用度向量,表征任务开始执行瞬间系统可能出现的所有工作状态的概率,反映星座的使用准备程度。
D:可信赖性矩阵,表征任务执行过程中系统从某一工作状态转移到其他工作状态的概率,反映任务执行过程中系统状态变化情况。
C:系统能力向量,任务过程中系统性能的度量,反映系统在可用及可信状态下完成任务目标的情况。
3 Markov-ADC星座评估模型假设
本文基于马尔科夫过程构建星座覆盖性能评估模型,描述星座状态转移情况,该模型的假设条件如下:
1)星座中各卫星同质化,即具有相同类型、相同型号等。
2)星座中各卫星只有两种状态:工作状态或故障状态,工作状态和故障状态可以以一定的概率相互转换。单颗卫星工作状态下的故障率为λ,即在Δt时间内发生故障的概率为λΔt;单颗卫星故障状态下的修复率为μ,即在Δt时间内被修复的概率为μΔt。
3)在一个状态转移时间间隔Δt内,单颗卫星保持原状态不变或最多只有一次状态转换过程,即工作状态→工作状态、故障状态→故障状态,工作状态→故障状态、故障状态→工作状态四种工作状态转换情况。
4)在一个状态转移时间间隔Δt内,可以存在多颗卫星发生状态转换。
4 星座状态定义
星座主要指多颗卫星相互协同,共同完成指定任务,提供通信、导航、遥感类服务。本文主要考虑对称的Walker星座,各卫星节点功能、效能一致。假设星座由N颗卫星组成,单颗卫星的故障率和修复率分别为λ和μ,在星座运行阶段有以下几种状态:
状态S0:星座中处于故障状态的卫星数量为0颗,处于工作状态的卫星数量为N颗。
状态S1:星座中处于故障状态的卫星数量为1颗,处于工作状态的卫星数量为(N-1)颗。
状态S2:星座中处于故障状态的卫星数量为2颗,处于工作状态的卫星数量为(N-2)颗。
……
状态SN:星座中处于故障状态的卫星数量为N颗,处于工作状态的卫星数量为0颗。
需要注意的是,处在同一状态的多颗故障卫星具有不同轨道分布情况,既可能分布在不同轨道面,也存在分布在同一轨道面的极端情况。不同故障卫星分布情况影响星座能力指标,其细分会导致状态组合爆炸问题,因此在仿真中随机选取故障卫星并统计其性能,在文中对同一星座状态下不同故障卫星分布不做考虑。
5 星座可用度
5.1 单星可用度
单星中断有四种基本类型[15]:短期计划中断、短期非计划中断、长期计划中断和长期非计划中断。由中断间隔时间和中断修复时间,得到单星的故障率和修复率。
单星的马尔科夫状态转移过程如图1所示。

图1 单颗卫星状态转移过程示意Fig.1 State transition process of single satellite
图中,0状态表示单颗卫星工作状态,1状态表示单颗卫星故障状态。用λ表示单颗卫星工作状态下的故障率,μ表示单颗卫星故障状态下的修复率,Δt表示状态转移时间间隔。
根据可靠性理论[15],得到单星稳态可用性α为:
5.2 星座可用度
星座总卫星数为N颗,在星座状态SK下,星座中处于故障状态的卫星数量为K颗,处于工作状态的卫星数量为(N-K)颗,单星可用性为α。由全概率组合公式得到,任务开始时刻星座处于该状态的概率AK为:
星座可用度向量A可以表示为:
A1×(N+1)=[A0,A1,…,AN]
6 星座状态转移概率
如图2为处于SK状态下星座状态转移过程示意图。

图2 卫星星座状态转移过程示意Fig.2 State transition process of constellation

(1)

(2)

(3)
由星座评估模型假设条件可知,在一个状态转移时间间隔Δt内,可以存在多颗卫星发生状态转换,即星座状态可在非相邻状态之间转移。
6.1 星座状态由SK转移到状态SK+q(q>0)
首先考虑星座状态由SK转移到状态SK+1的情况有:
(N-K)颗工作状态的卫星有1颗卫星发生故障;
(N-K)颗工作状态的卫星有2颗卫星发生故障,K颗故障状态卫星有1颗卫星修复;
(N-K)颗工作状态的卫星有(i+1)颗卫星发生故障,K颗故障状态卫星有i颗卫星修复;
……
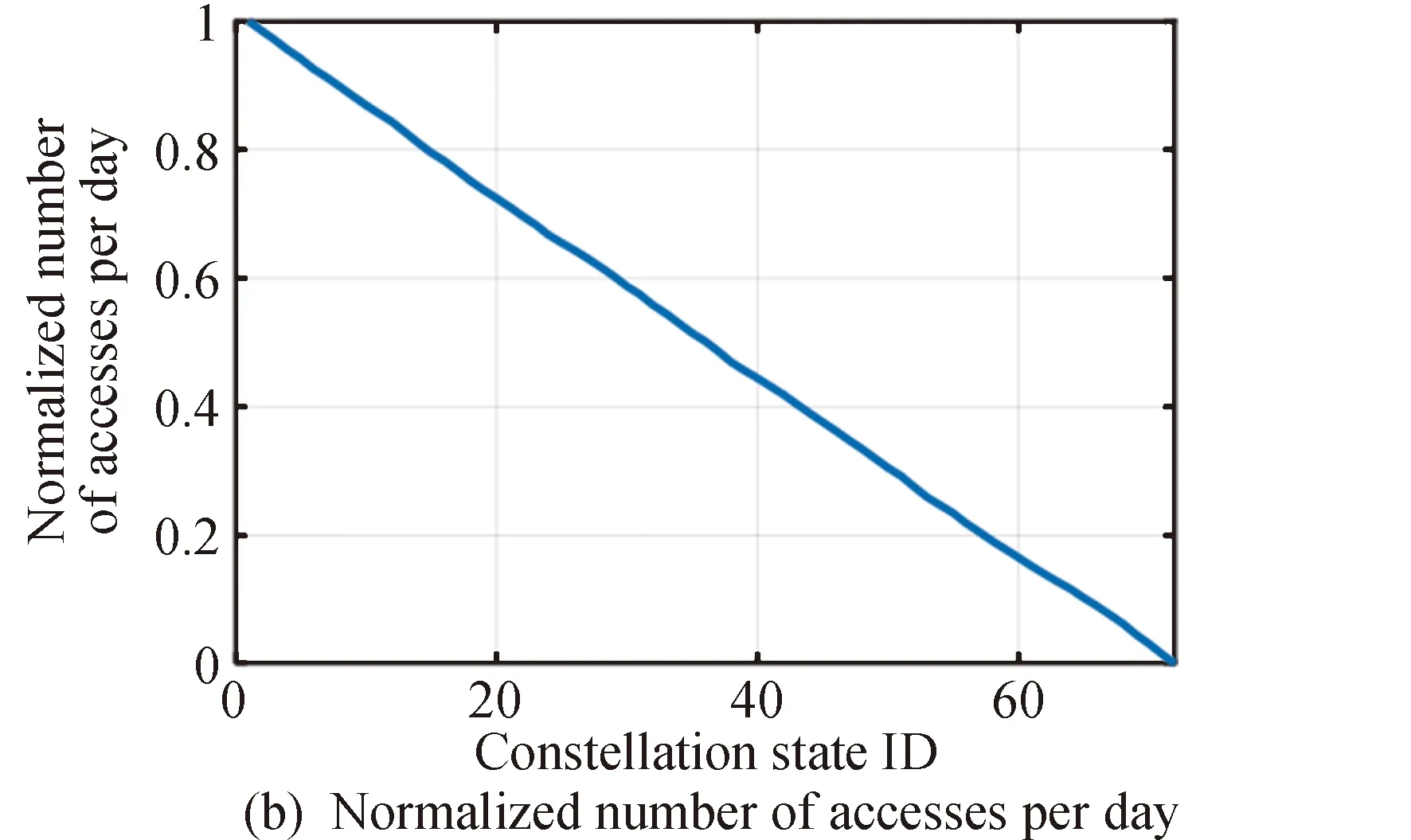
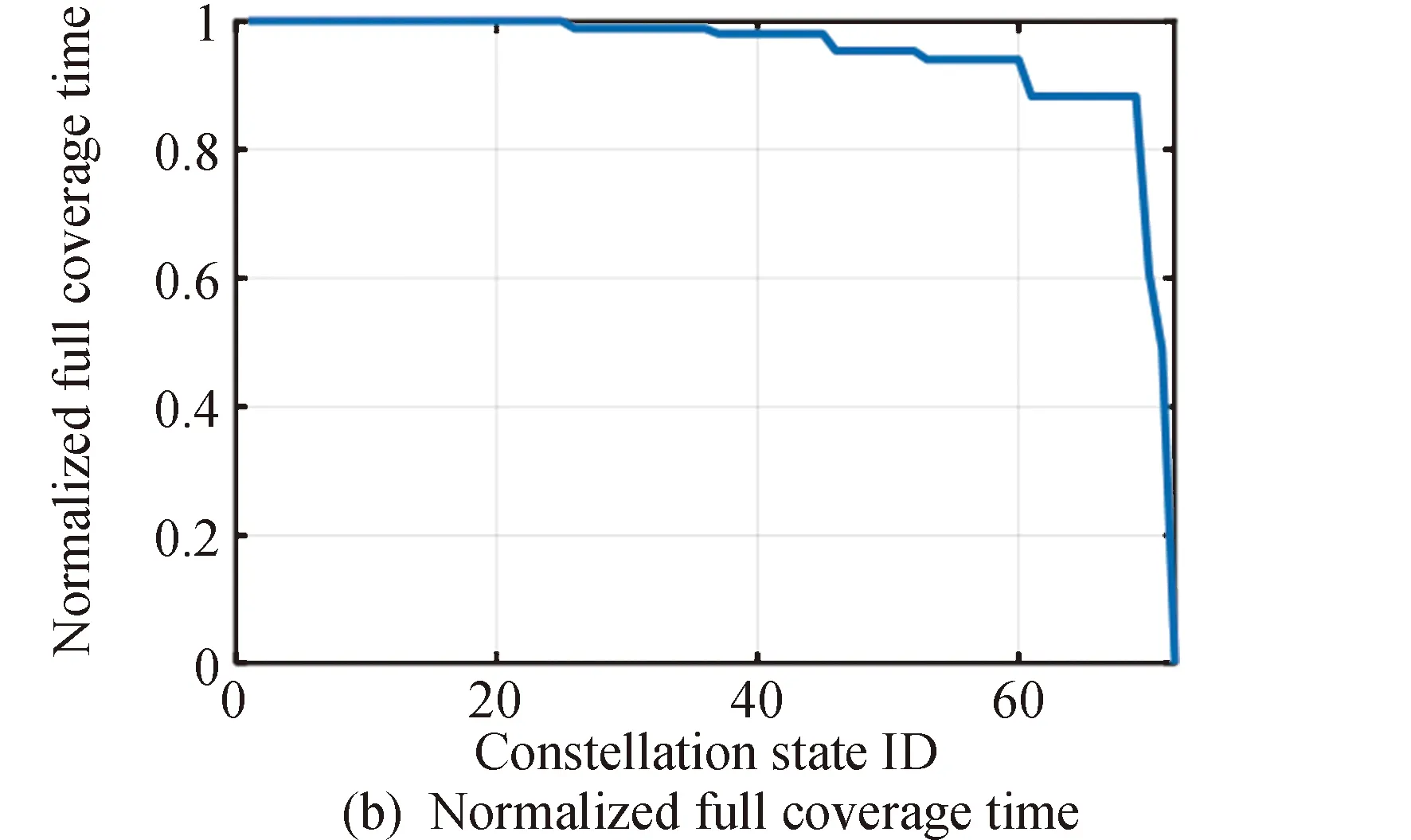
(N-K)颗工作状态的卫星有(K+1)颗卫星发生故障,K颗故障状态卫星有K颗卫星修复((K+1)≤(N-K))或(N-K)颗工作状态的卫星有(N-K)颗卫星发生故障,K颗故障状态卫星有(N-K-1)颗卫星修复((N-K-1) (4) 星座状态保持SK的情况有: (N-K)颗工作状态的卫星有0颗卫星发生故障,K颗故障状态卫星有0颗卫星修复; (N-K)颗工作状态的卫星有i颗卫星发生故障,K颗故障状态卫星有i颗卫星修复; …… (N-K)颗工作状态的卫星有K颗卫星发生故障,K颗故障状态卫星有K颗卫星修复(K≤(N-K))或(N-K)颗工作状态的卫星有(N-K)颗卫星发生故障,K颗故障状态卫星有(N-K)颗卫星修复((N-K) 星座状态由SK转移到状态SK-q的情况有: (N-K)颗工作状态的卫星有0颗卫星发生故障,K颗故障状态卫星有q颗卫星修复; (N-K)颗工作状态的卫星有1颗卫星发生故障,K颗故障状态卫星有(1+q)颗卫星修复; (N-K)颗工作状态的卫星有(i-q)颗卫星发生故障,K颗故障状态卫星有i颗卫星修复; …… (N-K)颗工作状态的卫星有(K-q)颗卫星发生故障,K颗故障状态卫星有K颗卫星修复((K-q)≤(N-K))或(N-K)颗工作状态的卫星有(N-K)颗卫星发生故障,K颗故障状态卫星有(N-K+q)颗卫星修复((N-K+q) 星座可信赖性矩阵D可以表示为: 其中,K=0,1,…,N,(K+q)=0,1,…,N。 星座覆盖性能主要考虑:覆盖重数、重访间隔、平均单日星座-目标连接数、全覆盖所需时长。 图3 覆盖性能指标参数Fig.3 Coverage performance parameters (1)覆盖重数 覆盖重数是在规定的时间、条件下,针对点目标,评估时间段内平均可见卫星数量的统计值;针对区域目标,评估时间段内所有网格点平均可见卫星数量的统计平均值。 (2)覆盖间隔 覆盖间隔是在规定的时间、条件下,评估时间段内卫星传感器与点目标/区域目标相邻两次覆盖时间间隔(当前覆盖结束与下次覆盖开始时间段)的统计平均值。 (3)单日平均连接数 单日平均连接数是在规定的时间、条件下,评估时间段内卫星传感器与点目标/区域目标建立连接次数的单日平均值。 (4)全覆盖所需时长 全覆盖所需时长是在规定的时间、条件下,卫星传感器完全覆盖目标区域所需时长。 不同类型卫星星座,对覆盖要求与侧重点不同。例如,通信卫星对覆盖间隔、单日平均连接数要求较高;遥感卫星侧重于覆盖间隔、全覆盖所需时长等指标;而导航卫星中覆盖重数对提供导航服务精度影响较大。在实际应用中,还需要根据星座类型依赖专家经验或人工智能方法等来调整指标权重值。下面给出评价星座覆盖能力的基本步骤。 7.2.1 指标归一化 由于各项指标的属性各不相同,需要对各项指标原始数据进行归一化处理。指标参数又分为正指标和逆指标,其中,正指标的指标数值与性能高低一致,逆指标的指标数值与性能高低相反。 假设有(N+1)个星座状态,M个指标参数,则对于第j个指标,其样本数据列为Xj=[x0j,x1j,…xij,…xNj]T,其中xij表示在第i个星座状态下,第j个指标的样本数据。对于正、逆指标进行归一化处理,得到矩阵R(N+1)×M=(rij)(N+1)×M。 其中,xjmax=max{xij};xjmin=min{xij}。 7.2.2 设置权重 权重的确定方法主要分为主观赋权法和客观赋权法等,其中主观赋权法受专家主观意愿影响比较大,而客观赋权法中的熵权法则是根据各项指标所含信息量的多少来确定其权重。 (1)主观赋权法 主观赋权法主要有专家咨询法、层次分析法等。各指标的权重由专家根据自己的经验和对实际情况的主观判断给出。其优点是可以根据指标的重要性给予相应的权重,重要的指标赋予较大的权重,不重要的指标赋予较小的权重,可根据实际需求赋予各项指标参数权重值。但由于指标的权重直接由专家给出,因此权重的合理性受到专家主观认识的影响,带有一定的主观性。 (2)熵权法 对于第j个指标,其信息熵计算表达式为: i=0,1,2,…,N;j=1,2,…,M 式中:(N+1)为星座状态数;M为指标参数个数。 各项指标参数权重值计算表达式为: 各项指标权重向量表示为: WM×1=[w1,w2,…,wM]T 7.2.3 系统能力 星座各状态系统能力向量C计算公式为: C(N+1)×1=R(N+1)×M×WM×1 以Walker星座作为分析对象,星座由9个轨道面,每个轨道面8颗共72颗卫星组成。轨道面高度640km,轨道倾角86°,8个轨道面分别定点于0°、40°、80°、120°、160°、200°、240°、280°、320°,轨道相位差5°。星载传感器为简单圆锥传感器,锥角设置为45°。 假设星座内每颗卫星[16]: 1)卫星每年调整轨道2次,每次持续12h; 2)卫星每年调整姿态6次,每次持续4h; 3)卫星每年发生4次可恢复性故障,每次需要2h恢复; 4)卫星设计寿命为3年,寿命末期可靠度0.8; 5)每颗卫星发生故障替换时间为0.1年。 目标区域设置为中国服务区内。 参考文献[16]中单星可用度计算方法,得到单星各项故障率和修复率: 根据各项故障率和修复率,综合得到单星的故障率和修复率: λ=λ1+λ2+λ3+λL=1.38×10-3(h-1) 单星可用性表达式为: 由全概率公式得到具有N颗卫星的星座初始状态为SK的概率为: 如图4所示为α=0.965时星座初始状态概率示意图。 图4 α=0.965时星座初始状态概率Fig.4 Initial constellation state probability when α=0.965 由星座状态转移概率公式得到,当λ=1.38×10-3(h-1),μ=3.81×10-2(h-1),Δt(1h)时间内星座状态转移矩阵为: (5) 由(5)可知,在Δt(1h)时间内,星座保持原状态概率最大。为估计星座长期状态转移情况,对星座多步状态转移概率进行了仿真计算,得到λ=1.38×10-3(h-1),μ=3.81×10-2(h-1),720Δt(3d)时间内星座状态转移矩阵: (6) 由(6)可知,在720Δt(3d)时,星座状态转移概率已经达到稳态值,星座状态为S2即星座中有2颗卫星处于故障状态的概率最大。 为分析单星故障率和修复率对星座状态转移概率的影响,将单星故障率由λ=1.38×10-3(h-1)降低为λ=0.8×10-3(h-1),保持单星修复率不变,得到720Δt(3d)时间内星座状态转移矩阵: (7) 由(7)可知,降低单星故障率后,星座状态向较低状态转移概率增大,如表2所示星座状态为S1即星座中有1颗卫星处于故障状态的概率最大。 为验证单星修复率对星座状态转移概率的影响,λ=0.8×10-3(h-1)不变,提高单星故障修复率令μ=6.0×10-2(h-1),得到720Δt(3d) 时间内星座状态转移矩阵: (8) 由(8)可知,提高单星修复率后,星座状态可进一步增大向更低状态转移概率,如上述矩阵所示星座状态为S0即星座中全部卫星处于工作状态的概率最大。 当单星故障率和修复率一定时,经过一段时间星座将进入稳定状态,且稳定状态与星座初始状态无关。降低单星故障率或提高单星故障修复率,都会促使星座向更好状态转移。在星座运行管理中,可以利用稳态转移概率来对单星故障率和单星故障修复率提出要求。 图5~8分别给出4个覆盖参数仿真性能,并对其进行归一化处理。 图6 重访时间随星座状态变化曲线Fig.6 Revisit time chaning with constellation state 图7 平均每日连接数随星座状态变化曲线Fig.7 The average daily number of accesses changing with constellation state 图8 完全覆盖所需时间随星座状态变化曲线Fig.8 The time required for full coverage changing with constellation state 由图5~8可知,覆盖重数和平均每日连接数参数为正指标参数,且符合一阶线性变化规律;重访时间和完全覆盖所需时间参数为逆指标参数,当故障卫星数达到一定值,指标性能迅速下降。 分别利用熵权法和主观赋值法得到四个覆盖指标的权重值,主观赋权法根据专家经验获得,分别对通信、导航、遥感星座各项指标参数进行赋值。表1给出熵权法和主观赋值法各项参数权重值。 表1 参数权重值Table 1 The weight of parameters 图9给出星座能力随星座状态变化曲线。遥感星座的重访时间和完全覆盖所需时间两个参数权重较大,由图6和图8可知这两个参数在故障卫星数较少时系统能力下降不明显,当故障卫星数达到一定值时系统能力迅速下降,因此在故障卫星数较少时遥感星座能力曲线相对于熵权法下降缓慢。同理,导航星座能力受覆盖重数参数影响较大,在故障卫星数较少时遥感星座能力曲线相对于熵权法下降较快。 图9 星座能力随星座状态变化曲线Fig.9 Constellation capability changing with constellation state 星座效能综合考虑星座可用度、星座状态转移情况以及系统能力,根据ADC公式可以得到不同权重赋值情况下720Δt(3d)星座效能评估值,如表2所示。 表2 星座效能评估值Table 2 Constellation effectiveness evaluation value 不同权重赋值情况下,同一星座的星座可用度和星座状态转移情况相同,星座效能值取决于系统覆盖能力。如表2和图9所示,星座效能值与星座覆盖能力曲线一致,遥感星座效能值较高,导航星座效能值较低。 本文通过Markov-ADC模型,将星座的初始状态、状态转移概率、覆盖能力结合起来,为复杂的星座系统建立合理、有效的效能评估指标体系提供了一种可行的参考方法,在一定程度上实现了对星座系统效能的定量化评估,对大型星座系统后续的建设与优化具有一定的参考价值。本文星座状态以故障卫星数量进行划分,未考虑故障卫星分布,如相同数量故障卫星分布在同一轨位和不同轨位情况对星座系统造成的影响不同,后续研究中可对此进行进一步细化研究。此外,Walker星座中各卫星节点重要性相同,对非对称星座应用具有一定的局限性。本文对星座评估只考虑了覆盖性能,后续可扩展从网络拓扑角度评估星座信息传输能力、从任务实施角度评估星座任务遂行能力,使得对星座的评估更加体系化、全面化。
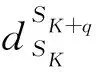

6.2 星座状态保持SK状态
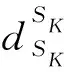
6.3 星座状态由SK转移到状态SK-q(q>0)

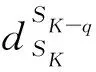
6.4 星座可信赖性矩阵
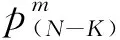
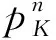
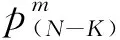
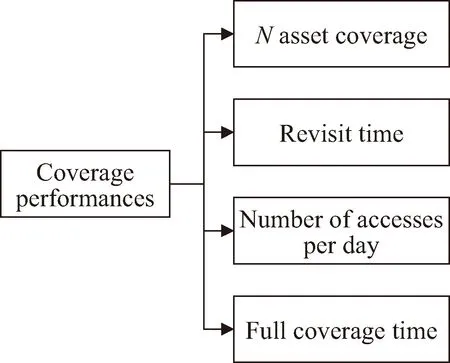
7 覆盖性能
7.1 覆盖性能指标选取
7.2 星座覆盖能力
8 仿真分析
8.1 单星可用度以及星座可用度

8.2 星座状态转移概率




8.3 覆盖性能仿真





8.4 权重系数与系统能力计算


8.5 星座效能评估

9 结论
