基于SOLO分类理论的小学数学表现性评价

吴存明

摘要：基于SOLO分类理论的表现性评价要有清晰的目标、真实的情境、挑战的任务和合适的量规，有明晰的课堂实施路径，即通过探学完成表现性任务，通过展学展开表现性对话，通过联学强调表现性关联，通过扩学实现表现性提升。基于SOLO分类理论的表现性评价使得评价学生的学习水平可视、思维结构可见，促进真学过程和实现深学结果。

关键词：SOLO分类理论；表现性评价；评价量规；小学数学教学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2023）19-0066-04

2022年版义务教育课程方案及各学科课程标准颁布以来，学生的学业评价得到广大教育工作者的关注。以小学数学为例，《义务教育数学课程标准（2022年版）》指出：“评价不仅要关注学生数学学习结果，还要关注学生数学学习过程，激励学生学习，改进教师教学。”[1]显然，新课标所提出的“教-学-评”一致性，目的是激励学与改进教。由此，促进学与教的表现性评价进入教学研究视域。本文尝试基于SOLO分类理论，对小学数学表现性评价做初步的探索与实践。

一、基于SOLO分类理论的小学数学表现性评价的内涵阐释

传统评价往往是与教学分开进行的，即教学在前、评价在后，如一堂课40分钟，一般前30分钟用于教学，后10分钟用于评价（练习）。而表现性评价作为一种有别于传统评价的新型评价方式，不仅具有检测、评估作用，更能够及时改进教师的教、促进学生的学。表现性评价的核心要素有四：一是教师要清晰、准确地把握教学目标及教学内容；二是基于真实、复杂的情境；三是设计挑战的任务，并要求学生完成任务、外显能力；四是有判断过程表现和结果的评价量规。这就形成了“目标—情境—任务—量规”的表现性评价的闭环。其中，表现性任务的实施需要一个合适的评价量规，SOLO分类理论就提供了一个较好的量规设计视角。“SOLO”（structure of observed learning outcom）意为“可观察的学习结果的结构”。SOLO分类理论针对儿童的不同表现水平，将儿童的认知发展分为5个从低到高的水平（如图1）[2]。

基于SOLO分类理论的表现性评价，即教师根据学生对完成任务的结果和具体表现，对学生的认知水平做出较为具体、明确的教学诊断。以小学数学为例，依据SOLO分类理论可以把数学学习表现分为优秀、良好、中等、合格、待努力等五个水平，具体见表1。

显然，处于E水平（前结构）层次的学生几乎不能建立知识结构，对表现性任务无从下手，找不到切入点。处于D水平（单点结构）阶段的学生，仅凭一条线索、一个论据即可跳到结论，这一水平的学生可以完成部分表现性任务。学生要深入理解基本的小学数学知识，必须努力达到最后三种能力水准，即C水平（多点结构）、B水平（关联结构）和A水平（拓展抽象结构）。SOLO分类理论为探寻学生的认知结构，促进学生认知水平的提升提供了切实可行、清晰可见的路径。

二、基于SOLO分类理论的小学数学表现性评价的实施路径

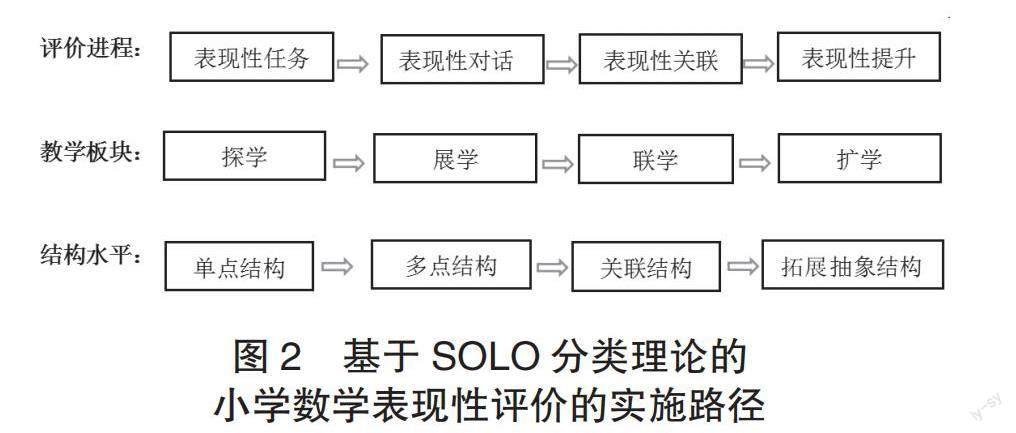
基于SOLO分类理论的表现性评价，就是要把“评”贯穿于“教”与“学”的全过程，可以基于“完成表现性任务→展开表现性对话→强调表现性关联→实现表现性提升”的实施路径，使得学生的思维结构不断进阶。其教学路径一般表现为“探学”→“展学”→“联学”→“扩学”四个板块，每个板块主要内容和表现性评价进程、预期的结构水平对应如图2。

下文以苏教版小学数学六年级上册“解决问题的策略（假设）”一课为例，具体阐释教学过程。

（一）探学：完成表现性任务——从“前结构”走向“单点结构”

面对新知，学生并不是“白纸”，因为许多新学知识都是他们的原初知识。如何激活学生的已有经验呢？在小学数学课堂上，由于课堂时空的局限性，表现性评价的实施一般采用任务单的形式。任务单的设计应该与教学目标相联系，聚焦真实的问题情境，助力学生探学。

例如，“解决问题的策略（假设）”一课的例题是：“小明将70毫升果汁倒入6个小杯和1个大杯，刚好全部倒满。已知小杯的容积都是大杯的?。小杯与大杯的总容积各为多少毫升？”这是一个条件齐全、答案唯一的良构问题，笔者在教材例题的基础上，設计了如下任务单：

任务：求小杯和大杯的容量

问题1：小明把720毫升果汁倒入6个小杯，正好都倒满。小杯的容量是多少毫升？

问题2：小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。小杯和大杯的容量各是多少毫升？

思考：为什么第2题不太好解决？

任务：如果给第2题补上一个条件：“小杯的容量是大杯的?”，你想到了什么？先用喜欢的方式画一画、写一写，最后再算一算。

上述任务单中，第1个问题只有一种量（都是小杯），可以直接“平均分”解决。而第2个问题是一个缺少条件的劣构问题——一方面由一种杯子变成了两种杯子，另一方面两种杯子的关系并没有告诉我们，会使学生陷入思维冲突中，反复思考题目的数量关系。最后出示完整的题目。教师的要求有些非常规，没有让学生去解题，而是让学生着力思考：由“小杯的容量是大杯的?”，你想到了什么？这是把学生学习的重心真正引到体会策略上去。

（二）展学：展开表现性对话——从“单点结构”走向“多点结构”

一般来说，大部分学生通常是发现了一个解决问题的思路，就直接算出答案，然后到此为止，即“单点结构”。要达到“多点结构”，学生需要通过展学对话，找到多个解决问题的思路，通过彼此欣赏、彼此对话，使自己的数学理解达到更深层次。通过展学，学生步入了形式化理解的层级。

在“解决问题的策略（假设）”一课探学板块后，学生主动对话，相互补充、纠正。有的学生认为：小杯等于大杯的?，也就是3个小杯看作1个大杯，一共3个大杯，因此720÷3得到1个大杯是240毫升，240÷3得到1个小杯是80毫升（方法1）。有的学生画线段图，得到3小段可以变成1大段，6小段这样就有2个大段，加上原来1大段一共就是3大段（方法2）。还有的学生先画6小段代表6个小杯，再画3小段表示1个大杯，就相当于9个小杯，720÷9得到1个小杯是80毫升，再用80×3得到1个大杯是240毫升（方法3）。还有的学生用解方程的方法，设1个小杯是x毫升，则1个大杯就是3x毫升，用3x+x=720，解方程得到x是180，3x是540（方法4）。此时，有学生指出：不应该是3x+x=720，这是1个大杯加1个小杯，应该是3x+6x=720，这才是1个大杯加6个小杯（方法5）。

（三）联学：强调表现性关联——从“多点结构”迈向“关联结构”

当学生有了形式化的理解后，还要关注所学知识之间的联系，找出相同点、不同点以及层次关系，最好是能形成一定的知识结构。如果能够建立起有效的认知结构，并将其作为内部学习系统的组成部分，那就说明已经理解了。

在“解决问题的策略（假设）”一课中，通过展学对话、彼此欣赏，许多学生似乎已经学会了多种计算方法，却不能建立这些方法之间的关联，这就需要进行关联融通，一方面对各种解题方法进行结构性的一一对应和深度关联，另一方面要从多种方法中抽象出“假设”策略，使得多元归一。

在教师的引导下，学生们发现很多方法是有联系的。有的学生发现方法1和方法2都是全部看作大杯，因此算式都是720÷3=240毫升，240÷3=80毫升。有的学生发现部分同学是先画图，找出解题思路，再列算式。还有的学生发现，方法3和方法5虽然一个列算式，另一个列方程，但都是全部看作小杯，用720÷9得到小杯，再求大杯。教室里响起了掌声。教师肯定大家的发现后，继续引导大家思考：这几种方法都用到了一个什么策略？有的学生说“替换”，把大杯替换成小杯，或者把小杯替换成大杯，一替换就把两种量变成一种量了，题目就好做了。还有的学生说是“假装”的策略，因为不是真的全部是小杯或者全部是大杯，这是“假的”。此时，教师相机板书课题：解决问题的策略（假设）。

（四）扩学：实现表现性提升——从“关联结构”跃至“抽象拓展结构”

如果要使学生的思维水平从“关联结构”跃至“抽象拓展结构”，就必须对所学内容进行横向扩展与纵向深化，这叫“扩学”。正如郑毓信教授提出的那样，“应帮助学生逐步学会‘反思……逐步学会更清晰、更深入、更全面、更合理地进行思考”[3]。

在“解决问题的策略（假设）”一课“扩学”板块中，教师相机把“小杯的容量是大杯的?”这个关键条件更改为“大杯的容量比小杯多20毫升”，引导学生思考：你能想到些什么？你还会做吗？有的学生假设全是小杯，求得一个小杯是（720-20）÷（6+1）=100毫升，则一个大杯是100+20=120毫升。还有的学生假设全是大杯，求得一个大杯是（720+6×20）÷（6+1）=120毫升，则一个小杯是120-20=100毫升。在随后的讨论中，教师引导学生思考“小杯的容量是大杯的?”换成“大杯的容量比小杯多20毫升”，在使用“假设”策略时有什么不同？有的学生认为“小杯的容量是大杯的?”是倍数关系，“大杯的容量比小杯多20毫升”是相差關系。还有的学生则发现：之前是总容量不变化，而杯子多少发生变化；之后则是杯子数不变化，而总容量发生变化。最后，教师提问：在我们之前的数学学习中，曾经用到“假设”策略，你能回忆出哪些？学生说出：三年级上册学估算，把乘数假设为最接近的整十数；在四年级上册学习了除数是两位数的除法，并将除数看作最近的整十数来试商；四年级下册学习解决问题的方法（画图），假设两位同学的邮票枚数一样多；六年级上册练习一道连加算式，可以假设成每个加数都是800，再来进行简便计算与调整……教师相机展示教材曾经用到“假设”策略的例题。

综上，表现性评价本身就是教学活动，在呈现表现性任务后，学生完成表现性任务，积极展开表现性对话，强调表现性关联，最终实现表现性提升。一言以蔽之，表现性评价即教学，表现性评价助教学。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022：4.

[2]约翰·B.彼格斯，凯文·F.科利斯.学习质量评价：SOLO分类理论[M].高凌飚，张洪岩，译.北京：人民教育出版社，2010：27.

[3]郑毓信.中国数学教育的“问题特色”[J].数学教育学报，2018，27（1）：6.

责任编辑：石萍