基于双拉普拉斯正则化与因果推断的多标签学习
2023-11-18高清维赵大卫卢一相
罗 俊,高清维,檀 怡,赵大卫,卢一相,孙 冬
(安徽大学 电气工程与自动化学院,合肥 230601)
0 概述
近年来,随着新兴互联网技术以及数据采集设备的日益更新,需要分析和处理的数据规模也日渐增大,随之而来的是关于这些庞大数据的分类问题。数据分类问题一般分为单标签分类和多标签分类。当样本数据只有1 个类别标签时,数据分类问题为单标签分类问题。而1 个样本数据具有多个类别标签时,就是多标签分类问题。多标签学习应用在各个不同场景中,例如,图像以及视频分类[1-2]、生物信息学[3-4]、文本分类[5-6]、文件分类[7]等。因此,多标签学习备受研究人员的广泛关注。
多标签学习算法在大多数情况下分为问题转换法和算法自适应法[8]。问题转换法是将多个单标签分类问题组合成多标签分类问题,典型的问题转换法 有MLC-LR[9]、标签幂级方法[10]、二元关联法[11]等。算法自适应法是优化传统单标签学习方法,用于处理多标签分类问题,如 ML-KNN[12]、RankSVM[13]以及多标签神经网络方法[14]等。尽管以上算法在分类效果上表现优异,但是上述多标签分类方法并没有考虑标签之间的关联信息。因此,研究人员相继提出众多关于学习标签相关性进行多标签分类的算法。根据标签之间相关性的不同,将多标签分类算法分为一阶方法、二阶方法和高阶方法[15]。一阶方法没有考虑标签相关性进行多标签分类[16-17]。二阶方法考虑了两两标签对之间的相关性进行多标签学习[18-19]。高阶方法则通过添加所有标签或标签集合的相关性进行多标签学习[20]。
与此同时,在处理多标签分类问题时,样本数据的特征往往都是高维的,这给数据分析、决策、筛选以及预测带来了巨大的挑战。在处理高维数据过程中会导致计算成本增加和存储资源的消耗,还存在过拟合问题[21-22]、维数灾难[23]等。因此,研究人员提出很多关于提取标签特定特征的算法进行多标签分类。LIFT[24]算法最早提出根据标签特定特征进行多标签学习,利用K-means 算法对每个类别标签进行聚类分析,根据聚类分析结果学习标签的特定特征,最后利用二元分类器进行多标签分类。MLLS[25]算法同时考虑了实例信息和标签信息学习通用特征和标签特定特征,最后进行多标签分类。此外,LF-LPLC[26]算法同时集成标签特定特征和局部成对标签相关性进行多标签分类。将原始特征空间转化为低维标签特定特征空间,采用最近邻算法考虑每对标签之间的局部相关性,用于扩展每个标签的特定特征,最后利用二元分类器进行多标签分类。LSGL[27]算法同时利用标签特定特征以及全局和局部相关性进行多标签学习,利用L1 范数提取每个类标签的标签特定特征,学习高阶全局标签相关性和标签局部平滑性,在学习低维标签特定特征表示后,利用二元分类器进行多标签分类学习。与此同时,LSDM[28]利用标签特定判别映射特征来解决多标签分类问题。LSDM通过聚类分析构建包含距离信息和空间拓扑结构的标签特定特征空间,利用线性判别分析挖掘每个标签的最优组合,最后进行多标签分类。然而,上述算法大多数并没有充分利用标签和特征的流形结构信息,导致生成次优结果。
在多标签学习研究中,特征信息和标签信息同样重要。最近的研究发现,引入流形学习方法可以充分利用标签信息和特征信息。例如,MDFS[29]算法利用流形正则化从原始特征空间生成低维嵌入,再利用标签的全局和局部相关性进行多标签特征选择。MRDM[30]算法将流形正则化和依赖最大化相结合进行多标签特征选择,该算法引入HSIC(Hilbert-Schmidt Independence Criterion)测量来评估流形空间和标签空间之间的依赖性。此外,DRMFS[31]算法同时采用特征图正则化和标签图正则化以保持特征和标签的几何结构进行多标签特征选择。为增强特征选择方法的鲁棒性,在损失函数中还添加了L1 和L2 范数。LA-ADMM[32]算法是一种增强型矩阵补全模型,在多标签学习中利用流形正则化处理标签缺失问题。该算法使用图拉普拉斯算子规范秩最小化过程,以确保标签空间上的标签平滑度。上述多标签学习算法均利用流形学习方法进行多标签学习。然而,在大多数情况下,它们都只是进行多标签特征选择,不能直接进行多标签分类。
本文提出一种结合标签特定特征、双拉普拉斯正则化和因果推断的多标签学习算法。利用线性回归建立多标签模型的基本分类框架,通过标签之间的因果关系提高模型性能。在投影过程中,通过标签几何结构以及特征相似度组成双拉普拉斯正则化,有效保持数据的局部流形结构。本文将标签因果推断以及双拉普拉斯正则化联合在1 个整体的框架中,可以有效提取标签特定特征并进行多标签分类。
1 多标签学习
1.1 线性回归模型建立
在多标签学习中设实例特征矩阵X=[x1,x2,…,xn]T∊Rn×d相应的标签矩阵为Y=[y1,y2,…,yn]T∊Rn×m,其中,n代表数据集的实例个数,d为数据集的实例特征个数,m为数据集的标签个数。多标签训练集设为S={(xi,yi)|(1 ≤i≤n)},其中,xi={xi1,xi2,…,xid} 为实例特征向量,yi={yi1,yi2,…,yim}为标签向量。当标签yi属于实例xi时,yij=1,否则yij=0。
多标签分类的目标是建立1 个映射关系:f:X→2Y。由LLSF[33]可知,每个类别标签都具有标签特定的特征,并且与原始特征相比,这些标签的特定特征是稀疏的。因此,与LLSF 类似,在处理多标签分类问题时,通过线性回归模型和L1范数正则化学习标签的特定特征[34]。优化的目标函数可定义为:
其 中:W=[w1,w2,…,wm]Τ∊Rd×m为系数矩阵;L1 范数正则化可以模拟标签的稀疏化过程;β为权衡系数,控制模型的复杂度,避免模型过拟合。W中的非零元素可以确定标签的特定特征,因此,通过学习系数矩阵W可以有效区分相应的类别标签。
1.2 因果推断
在多标签学习研究中可以发现,标签之间存在较强的关联性。为提高模型的分类能力,探索标签之间的潜在关系具有重要的研究意义。
当标签之间存在强关联性时,对应的特征也有类似的关联性。假设2 个不同的标签yi和yj具有强相关性,它们对应的标签特定特征wi和wj具有较高的相似性。反之,在不相关标签之间的标签特定特征就不相似。因此,本文采用一种新颖的标签因果相关性来优化模型,利用标签之间的因果关系提高模型性能。优化的目标函数可以写为:
其中:R∊Rm×m表示标签因果关系矩阵;α为权衡系数,用于控制标签因果关系对模型系数W的相对重要性。由于标签因果关系为非对称的,因此R为1 个非严格对称的矩阵。为了防止R对优化目标函数中的第2 项产生不利影响,本文将R定义为R=(R+RT)/2。此外,对于式(2)中的第2 项,本文采用因果学习机[35]学习标签之间的因果关系,其中标签因果关系矩阵R通过GSBN[36]算法计算得到。在考虑标签因果关系的基础上,本文利用常用的欧氏距离度量标签特定特征之间的相似性。当标签yi和标签yj具有因果相关性时,对应的系数向量wi和wj往往会非常接近,即标签的特定特征具有强相似性。
1.3 双拉普拉斯正则化
式(2)的优化目标是生成标签的特定特征,用于多标签分类。这个过程可以被认为是从高维的实例特征空间中学习一种低维的映射表示,然后进行多标签分类。在映射过程中,本文最大的目标是减少原始数据的冗余特征,使学习到的低维特定特征对标签具有较强的辨识度[37]。在以往的研究中,保持原始特征数据的局部流形数据结构至关重要[38-39]。因此,本文在投影过程中加入双拉普拉斯正则化,进而有效地保持原始数据的局部流形结构。式(2)的目标函数可以优化为:
其中:L1(W)和L2(W)为双拉普拉斯正则化;λ1和λ2为相应的平衡参数,用来权衡局部结构对模型系数的相对重要性。
根据问题假设,对于式(3)中的第4 项,如果原始特征xi和xj结构相似,那么它们的低维映射表示也应该是相互封闭的,即对应的系数向量wi和wj是相似的。因此,本文构建以下模型捕捉特征之间的局部关系。该正则化可以根据特征xi和xj之间的相似性调整系数向量wi和wj,其表达式为:
其中:Sij为特征亲和力矩阵的第i行第j个元素。本文采用高斯核函数定义Sij:
其中:t∊R;Nk(wi)表示wi的第k个近邻集。通过以下推导,L1(W)可以写成如下形式:
其中:M∊Rd×d为对角矩阵;LS=M-S为对应的拉普拉斯矩阵。
另一个拉普拉斯正则化项为式(3)中的最后一项。如果标签yi和标签yj非常接近,那么它们对应的xiW和xjW也应该更加紧密。因此,构建标签图的拉普拉斯正则化,根据标签yi和yj的相似度调整系数矩阵W,使得W能更好地学习标签特定特征用于多标签分类,其表达式如下:
其中:P∊Rn×n为对角矩阵为P的 第i个 对角元素为标签相似度矩阵A的拉普拉斯矩阵;Aij为标签相似度矩阵A第i行、第j列的元素,表示标签yi和yj之间的相似度。标签相似度矩阵A可以采用多种方法给出,利用核函数构造标签关联矩阵A:
其中:t∊R。综上所述,本文最终的目标函数可以优化为:
从式(9)目标函数的优化模型中可以看出,在基本的线性多标签分类模型框架下,本文通过特征相似度和标签几何结构组成的双拉普拉斯正则化、标签因果关系建模多标签分类模型。因此,本文将标签因果关系以及双拉普拉斯正则化联合在1 个整体的框架中,不仅可以有效提取标签的特定特征,而且还可以进行多标签分类。
2 MLDL 模型的求解
2.1 目标函数优化
本节目的是对MLDL 模型进行求解,由式(9)可以看出,目标函数的最小化问题是1 个凸优化问题。在凸优化问题中存在目标函数不可微的情况。一般的解决方案是通过迭代引入次梯度法(SD)[40]或者引入交替方向乘子法(ADMM)[41]。然而,次梯度法的收敛速度比梯度下降法慢,同时ADMM 需要在非光滑目标函数的基本框架上引入多个辅助变量乘子,极大程度地减慢算法的收敛速度。当凸函数整体不可微但非光滑可以分解为可微和不可微函数时,加速近端梯度算法的收敛速度可以达到二阶收敛,相比其他方法有明显的速度优势。同时由于L1 范数正则化具有不光滑性,因此目标函数的优化趋于非光滑。受文献[42]的启发,通过加速近端梯度法(APG)[43]求解目标函数。在式(10)中,本文用Φ表示模型系数。由APG 算法可知,目标函数的凸优化问题可以写成:
其中:Η 为希尔伯特空间;f(∙)为凸可微函数;g(∙)为凸不可微函数。fW(Φ)和gW(Φ)可以表示为:
APG 算法并不是直接最小化F(·),而是最小化F(·)的可分离2 次接近序列Q(·),记为:
其 中:(·)+=max(·,0);1 ≤i≤d;1 ≤j≤l。
为证明式(9)的利普希茨连续性,根据式(15)和西尔维斯特不等式,得到如下结论:
本文在算法1 中总结利用APG 算法求解MLDL的优化步骤,将训练数据集X∊Rn×d、标签训练矩阵Y∊Rn×m、权重参数α、β、λ1、λ2、γ作为输入,最终经过迭代求出模型系数矩阵W,得到学习到的标签特定特征。步骤主要有:
1)初始化:b0=b1=1,k=1,W0=W1=(XΤX+γI)-1XΤY;
2)采用因果学习机计算标签因果矩阵R;
3)利用式(5)计算特征亲和力矩阵S,并且计算LS=M-S;
4)利用式(8)计算标签关联矩阵A,并且计算
5)利用式(21)计算利普希茨常数Lf;
10)k=k+1;
11)直到收敛。
此外,算法2 总结本文所提MLDL 算法的测试过程。利用算法1 得到的模型系数矩阵W和测试集Xtest,以及阈值τ,Ytest给定阈值τ通过Sign(Stest-τ)获得预测的标签Ytest,其中Stest=XtestW。MLDL 算法将生成标签特定特征与后续分类模型统一到1 个框架中进行多标签分类。当学习到标签的特定特征之后,MLDL 还可以结合二元分类器进行多标签分类。
2.2 MLDL 算法复杂度分析
本节主要对MLDL 算法优化部分的复杂度进行分析,算法的复杂度主要取决于算法不收敛时的迭代过程。在MLDL 算法中,X∊Rn×d,Y∊Rn×m,W∊Rd×m,R∊Rm×m,其中,n表示样本个数,d表示样本维数,m表示类标签个数。迭代中最耗时部分为式(17),其复杂度为O(d2m+ndm+dm2),当进行t次迭代时,总的时间复杂度为O((n+d+m)mdt)。实验中,迭代次数一般不超过80 次。当训练数据集满足n≫d>m时,MLDL 的时间复杂度与样本数量n成正比。此外,由于本文学习的标签特定特征W是稀疏的,因此实际时间成本将更低。
3 实验结果及分析
3.1 数据集
为验证本文提出的MLDL 算法的有效性和竞争性,本文在10 个基准多标签数据集上进行大量实验评估算法性能。实验中所用的数据集可以在Mulan(http://mulan.sourceforget.net/datasets-mlc.html)和Yahoo(http://www.kecl.ntt.co.jp/as/members/ueda/yahoo.tar)下载。表1 所示为数据集的详细信息。
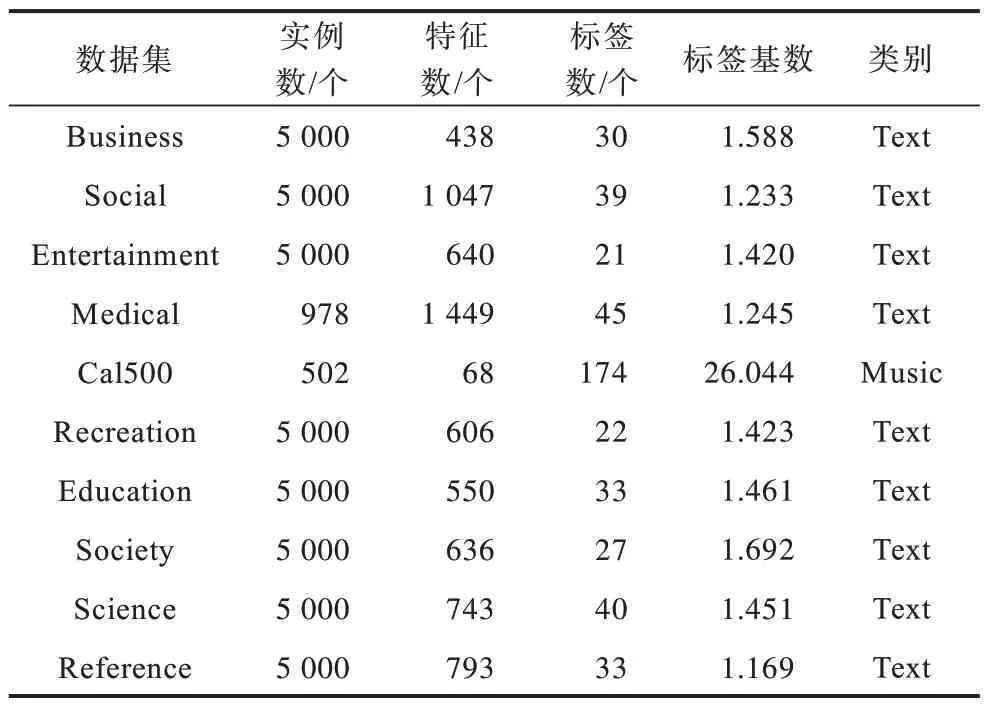
表1 数据集的详细信息Table 1 Detailed information of datasets
3.2 对比算法
在本节中将最先进的8 种算法和MLDL 算法的实验结果进行比较。MLDL 算法可以单独进行多标签分类,也可以在提取标签特定特征之后和其他分类器组合,实验时所采用的是BSVM 分类器。此外,对比算法和MLDL 算法均对训练数据集进行五折交叉验证,缓解模型过拟合问题以及避免数据集划分不合理导致实验结果可靠性降低。对比算法的模型参数均采用原始文献中提供的范围进行网格搜索得到的。
1)LLSF[33]是一种在基于标签特定特征的多标签分类方法。模型参数α,β∊{2-10,…,210},阈值τ=0.5。
2)LIFT[24]探索每个标签的正负实例聚类结果,学习标签特定特征进行多标签分类。聚类比率r=0.1。
3)ML-KNN[12]是一种多标签学习的懒惰学习方法,通过经典的k 近邻方法进行多标签分类。本文实验中最近邻数k=10,平滑参数s=1。
4)JLCLS[44]是一种联合标签补全和标签特定特征的多标签学习方法,模型参数α、β和θ取值范围为{2-10,2-9,…,29,210},γ的取值范围为{0.1,1,10}。
5)BDLS[45]是一种基于双向映射和标签特定特征进行多标签分类方法。模型参数α、λ和β区间为{2-7,2-6…,26,27},γ的取值范围为{0.01,0.1,1,10},阈值τ=0.5。
6)LSGL[27]是一种联合学习标签特定特征以及全局和局部标签相关性的多标签分类算法。在{10-3,10-2,…,102,103} 中寻找折中参数λ1,在{10-3,10-2,…,101}中寻找λ2、λ3、λ4、λ5。
7)WRAP[46]是一种在嵌入特征空间学习标签的特定特征进行多标签分类算法。模型参数λ1、λ2取值范围为{0,1,…,10},λ3=0.1,α=0.9。
8)MLDL 是本文提出的一种联合双拉普拉斯和因果推断的多标签分类方法。模型参数α、β、λ1和λ2的区间为{2-7,2-6,…,23,24},阈值τ=0.5。
9)MLDL-SVM 利 用MLDL 提取标签的特定特征,再通过SVM 训练每个二分类器进行多标签分类。模型参数α、β、λ1和λ2取值范围和MLDL 相同。
3.3 实验环境与评价指标
本文在Windows 10、Intel®CoreTMi7-7700K、16 GB RAM 上进行实验,方法在MATLAB 2016b 中实现。本文选取6 个广泛使用的多标签分类评价指标对每种算法进行评价,包括汉明损失(Hamming Loss,HL)[47]、1 次错误率(One Error,OE)[47]、覆盖率(CV)[47]、排序损失(Ranking Loss,RL)[47]、平均精度(Average Precision,AP)[47]、ROC 曲线下的面积(AUC)[48]。AP 和AUC 值越大,算法性能越好,而其他值越小,算法性能越好。给定测试集Dt=设h(xi)为多标签分类器,f(xi,y)为预测函数,rankf为排序函数。
HL 计算错误分类的实例标签对数量,表示实例样本的实际标签和预测标签之间的错误匹配数量。汉明损失的计算式如下:
AP 计算特定标签排列的正确标签的平均分数,计算式如下:
OE 计算排名最高的标签不在相关标签集中实例的得分,计算式如下:
RL 评估不相关标签的排名高于相关标签的指标,计算式如下:
CV 用于评估遍历给定样本的所有相关标签的平均步数指标,计算式如下:
AUC 评估所有类别标签的平均AUC,计算式如下:
3.4 结果分析
本文介绍9 种算法在10 个数据集上的实验结果。对于每个数据集,使用5 倍交叉验证进行系统评估,将数据集的80%作为训练集,20%作为测试集,对所有算法进行5 次重复实验,得到实验结果如表2~表7 所示,加粗表示最优数据。本文从表2~表7的实验结果得到如下结论:
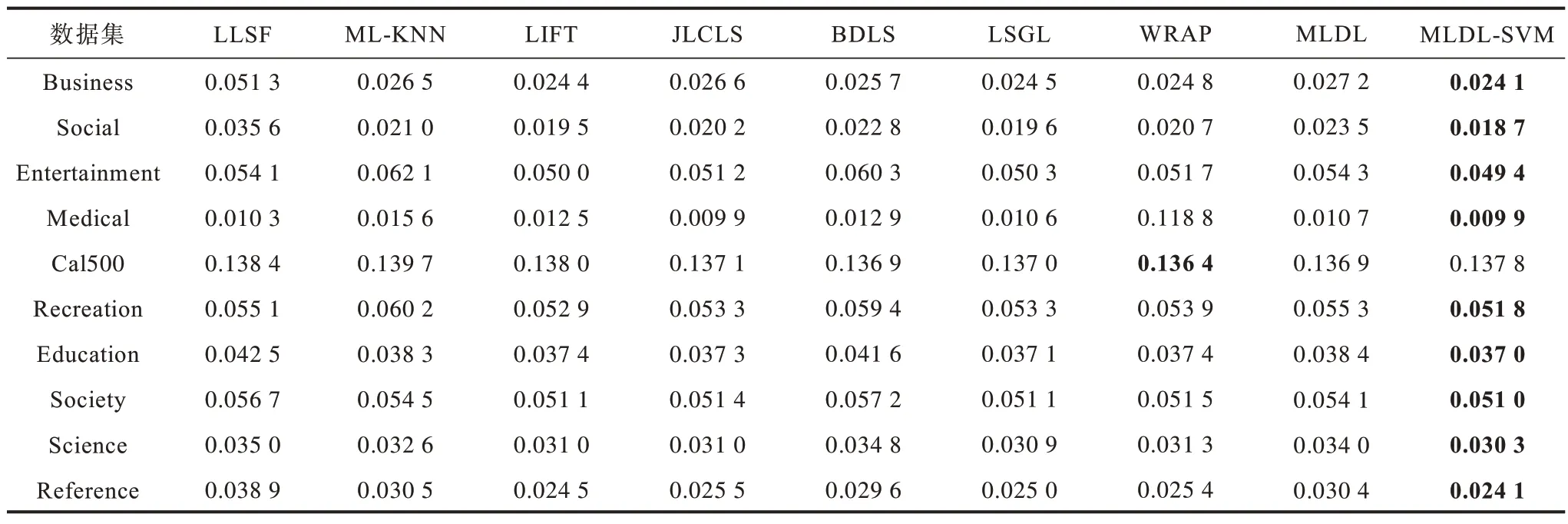
表2 在10 个数据集上不同算法的的汉明损失Table 2 Hamming loss among different algorithms on ten datasets
1)从表2 和表3 可以看出,除了Cal500 以外其他数据集上MLDL-SVM 的HL 和AP 都表现最佳的性能。从表4 可以看出,在所有数据集上MLDL-SVM算法的OE 都优于其他算法。从表5 可以看出,MLDL-SVM 在7 个数据集上RL 最佳,其次是LIFT和WRAP。从 表6 和表7 可以看出,在Social、Entertainment 等数据集上MLDL-SVM 表现出最优的实验结果。因此,本文提出的MLDL-SVM 算法具有更优的性能。
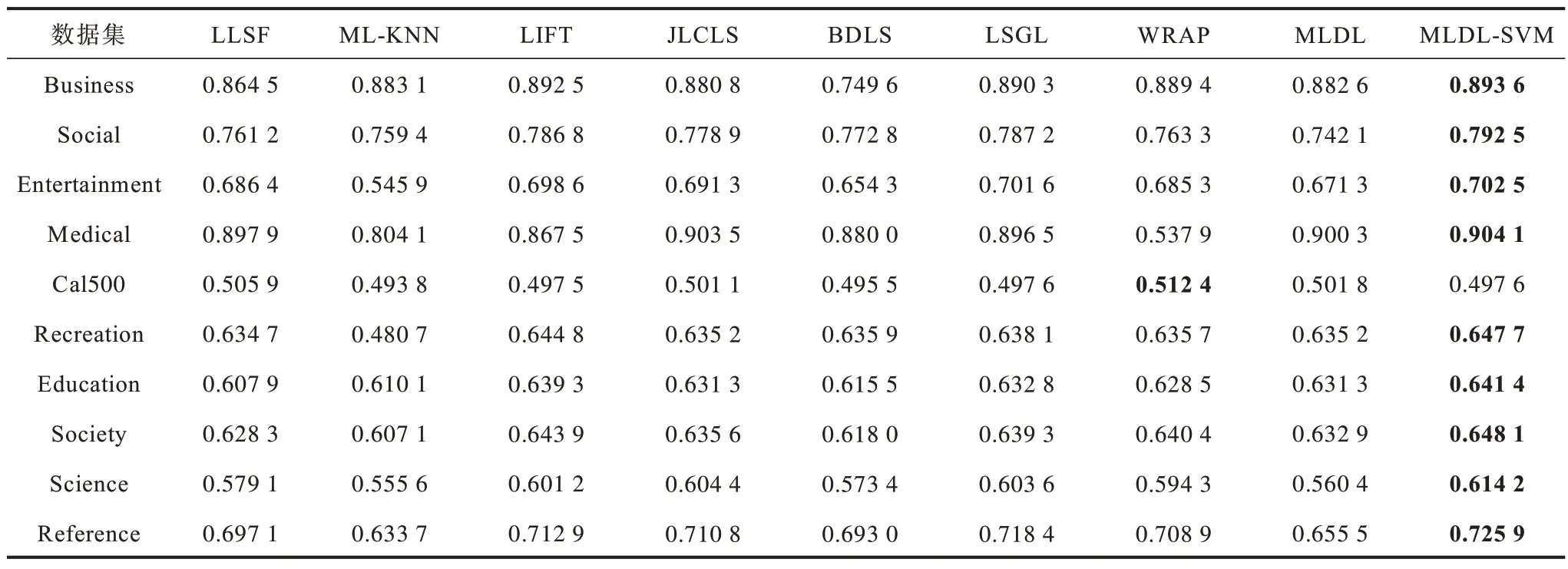
表3 在10 个数据集上不同算法的平均精度Table 3 Average precision among different algorithms on ten datasets
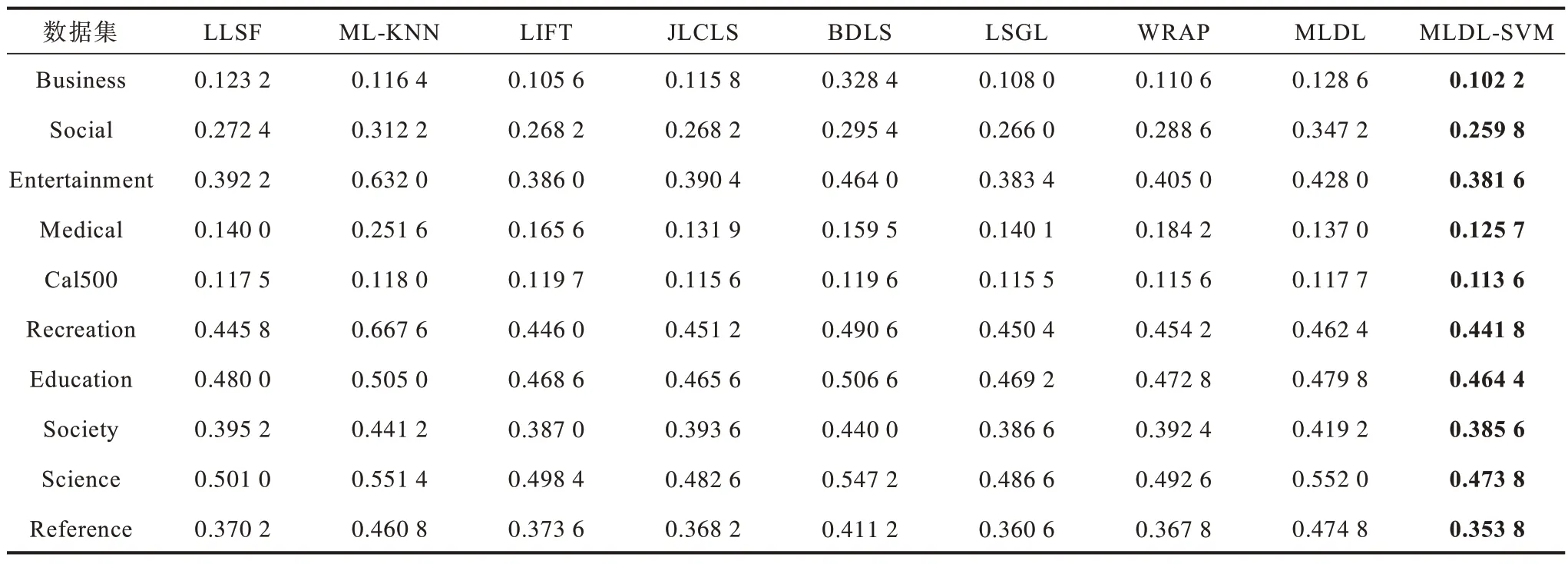
表4 在10 个数据集上不同算法的1 次错误率Table 4 One error among different algorithms on ten datasets
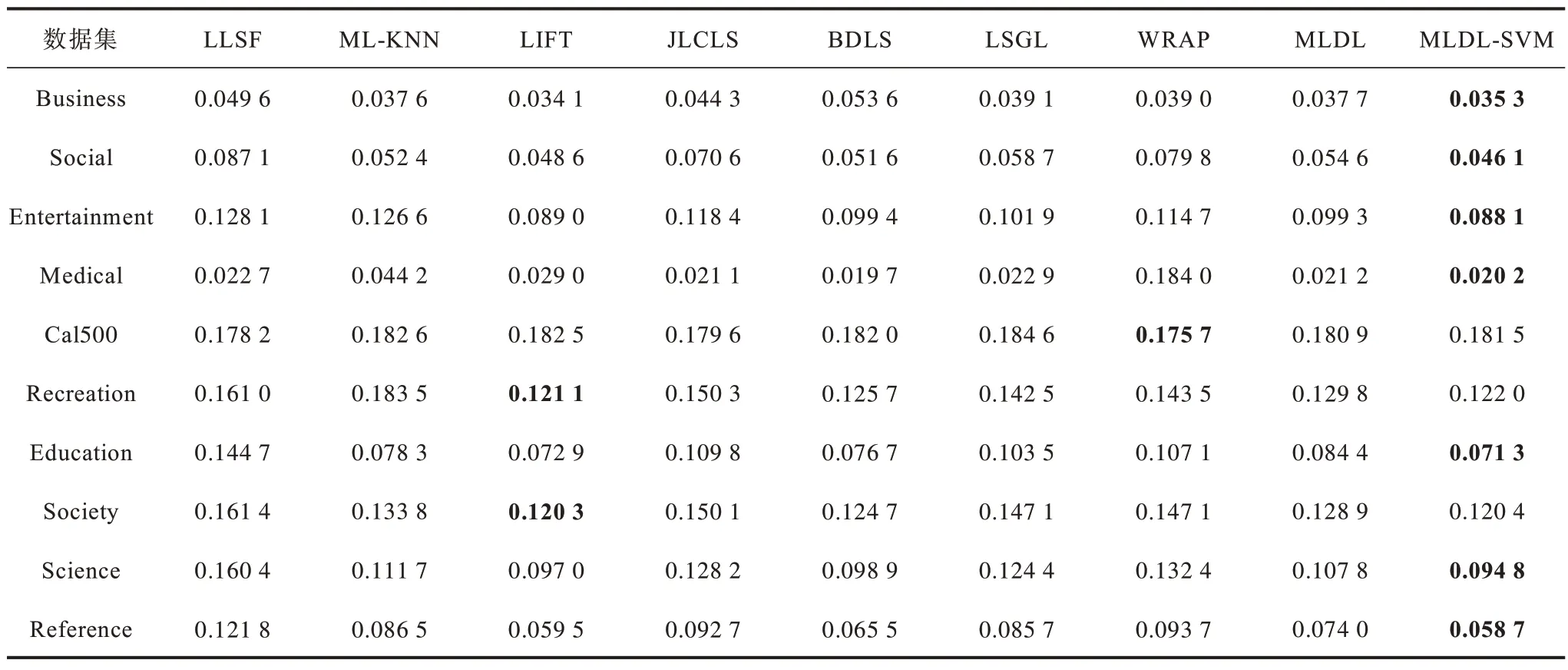
表5 在10 个数据集上不同算法的排序损失Table 5 Ranking loss among different algorithms on ten datasets
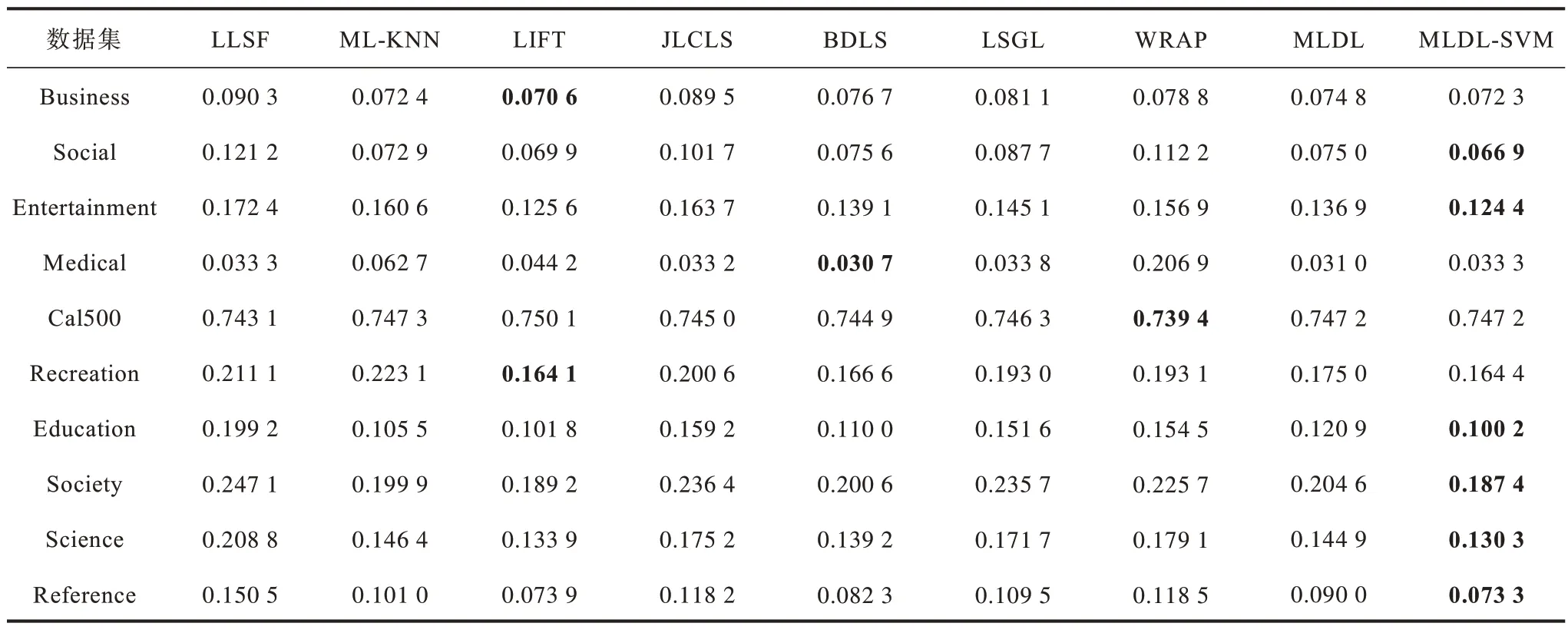
表6 在10 个数据集上不同算法的覆盖率Table 6 Coverage rate among different algorithms on ten datasets
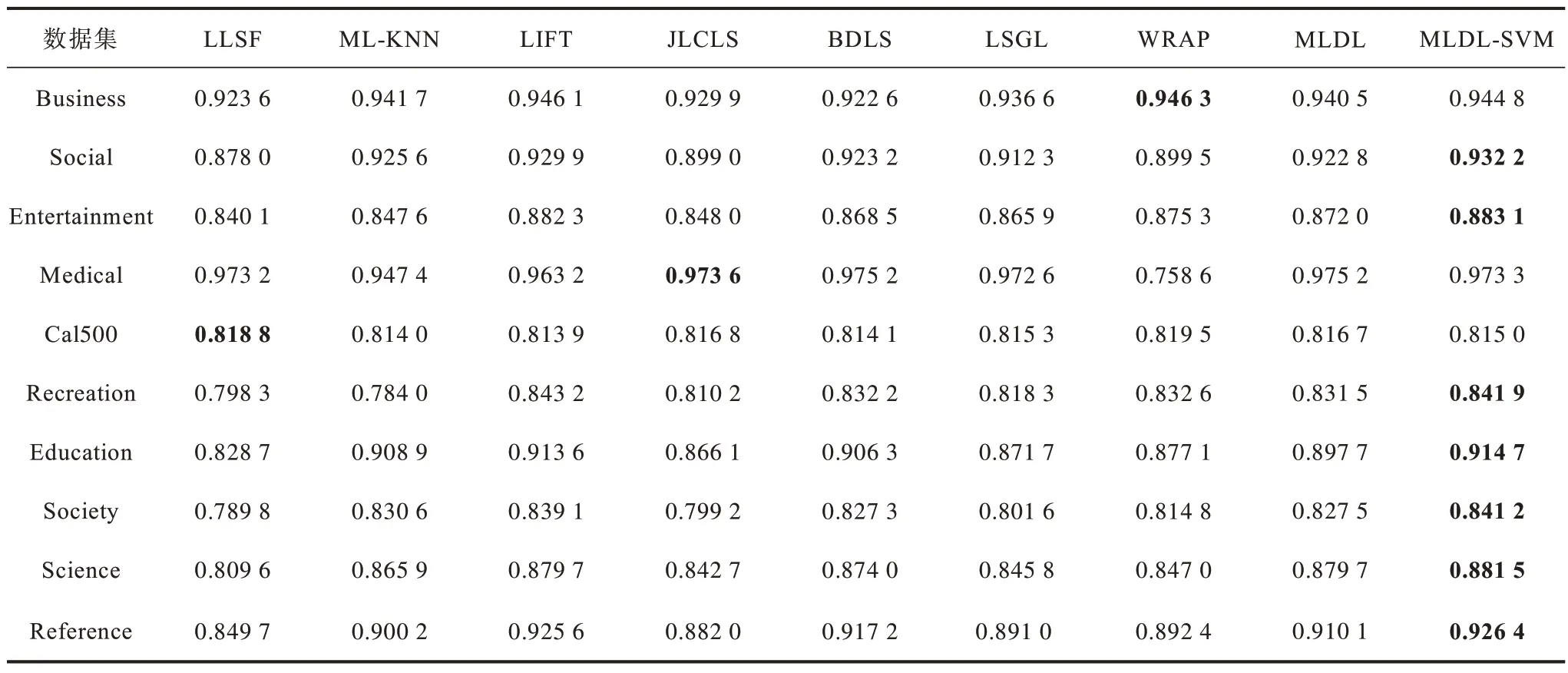
表7 在10 个数据集上不同算法的AUCTable 7 AUC among different algorithms on ten datasets
2)从整体上看,在Social、Entertainment、Education、Science 和Reference 5 个数据集上,MLDL-SVM 算法相较于其他算法均表现出更优的性能,说明本文提出的MLDL-SVM 具有一定的有效性和竞争性。
3)通过比较MLDL-SVM、MLDL、LIFT 算法的实验结果可以看出,在大多数情况下,MLDL-SVM算法性能更优。由于LIFT 算法和MLDL-SVM 算法类似,都是先提取标签特定特征再用SVM 进行多标签分类,因此进一步说明本文所提算法在提取标签特定特征上的有效性。
为进一步验证MLDL 和MLDL-SVM 算法的有效性,本文采用额外的统计假设检验方法对所有对比算法的相对性能进行评估。本文采用Friedman 检验方法[49]进行性能分析。表8 所示为在6 个评价指标下MLDL-SVM 对应的Friedman 统计量FF。当临界值α=0.05 时,评价指标下的值为2.069 8。基于此,本文采用Nemenyi 检验[49]作为事后检验方法比较各个对比算法的性能,进一步验证MLDL 和MLDL-SVM 算法的竞争性。如果2 个算法的平均排序小于临界差异(Critical Difference,CD)(CCD=,则认为2 个算法之间没有显著性差异。相反,若2 个算法之间的平均排名大于临界值时,说明2 种算法具有显著差异。
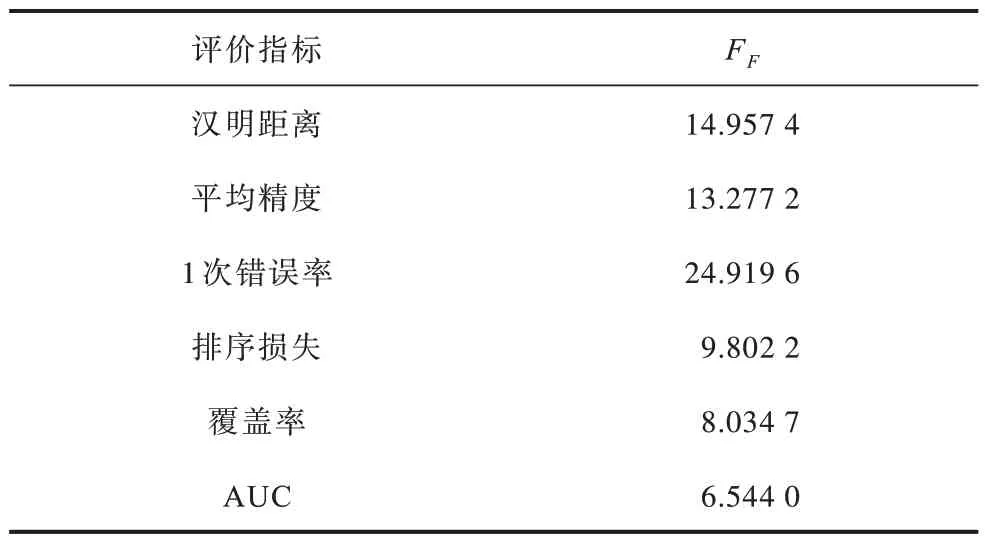
表8 在评价指标下MLDL-SVM 对应的Friedman 检验Table 8 Friedman test corresponding to MLDL-SVM under evaluation indicators
当显著性水平α=0.05 时,qα=3.102,CCD=3.799 2(k=9,N=10)。图1 所示为在6 个评价指标下9 种对比算法的临界差异图。实线连接表示算法之间没有显著性差异,相反,没有被实线连接的算法之间具有显著性差异。
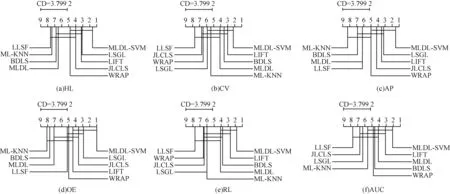
图1 不同算法的临界差异示意图Fig.1 Schematic diagram of critical difference among different algorithms
从图1 可以看出,当实线将MLDL-SVM 算法和其他比较算法相连接时,表示MLDL-SVM 算法和该算法没有显著性差异。由图1(a)可知,在HL 评价指标上,MLDL-SVM、LSGL、LIFT、JLCLS 和WRAP 算法之间没有显著性差异。从图1(b)可以看出,在CV 评价指标上MLDL-SVM 分别和WRAP、JLCLS、LLSF 具有显著性差异。从图1(c)可以看出,在AP 评价指标上MLDL-SVM、LSGL、LIFT、JLCLS 和WRAP 算法之间没有显著性差异。从图1(d)可以看出,在OE 评价指标上MLDL-SVM、LSGL、LIFT 和JLCLS 算法之间没有显著性差异。此外,从图1(e)可以看出,在RL 评价指标上MLDL-SVM、BDLS、LIFT 和MLDL 算法之间无显著性差异。从图1(f)可以看出,在评价指标AUC上MLDL-SVM 分别与LLSF、JLCLS、LSGL 存在显著性差异。因此,在50%的情况下,MLDL-SVM 算法显著性优于其他算法。
从整体上看,MLDL-SVM 算法在6个评价指标上的平均排名均最优。通过比较MLDL-SVM 和LIFT可以看出,在同样采用BSVM 作为分类器时,MLDLSVM 算法优于LIFT 算法,侧面反映MLDL-SVM 在提取标签特定特征上比LIFT 更优。
比较MLDL 和BDLS 算法可以看出,在多数情况下2 种算法无显著性差异,然而MLDL 在HL、AP和AUC 上具有更优的排名。其原因为MLDL 加入双拉普拉斯正则化,充分利用标签和特征的信息,因此具有较优的分类效果。
3.5 参数敏感性分析
本节进行MLDL 的参数敏感性分析实验。在MLDL 算法中有4 个重要的平衡参数α、β、λ1和λ2。α控制标签因果关系对模型系数的影响。β控制模型系数W的稀疏性。λ1和λ2分别控制标签局部流形结构和特征局部流形结构对模型系数的影响。图2所示为MLDL 算法在Medical数据集上AP、RL 和HL 的评价指标,并且在其他数据集上也有类似的结果。图2(a)所示为当固定参数λ1和λ2时,参数α和β在区间{2-5,2-4,…,24,25}上的变化曲线图。图2(b)所示为固定参数α和β时,参数λ1和λ2在区间{2-5,2-4,…,24,25}的变化曲线,通过网格搜索得到固定的参数。从图2可以看出,当β过大时,MLDL 的性能较差。由于β控制着模型系数的稀疏性,β过大使得MLDL 无法有效提取标签的特定特征。此外,当λ1过小时,MLDL 性能也较差。该结果进一步说明标签的局部流形结构在MLDL 中的重要作用。因此,参数λ1不能设置太小。MLDL 在大多数情况下对参数α和λ2不敏感。从图2 可以看出,每个参数在一定范围内是相对不敏感的,超过一定范围算法的性能就会下降。
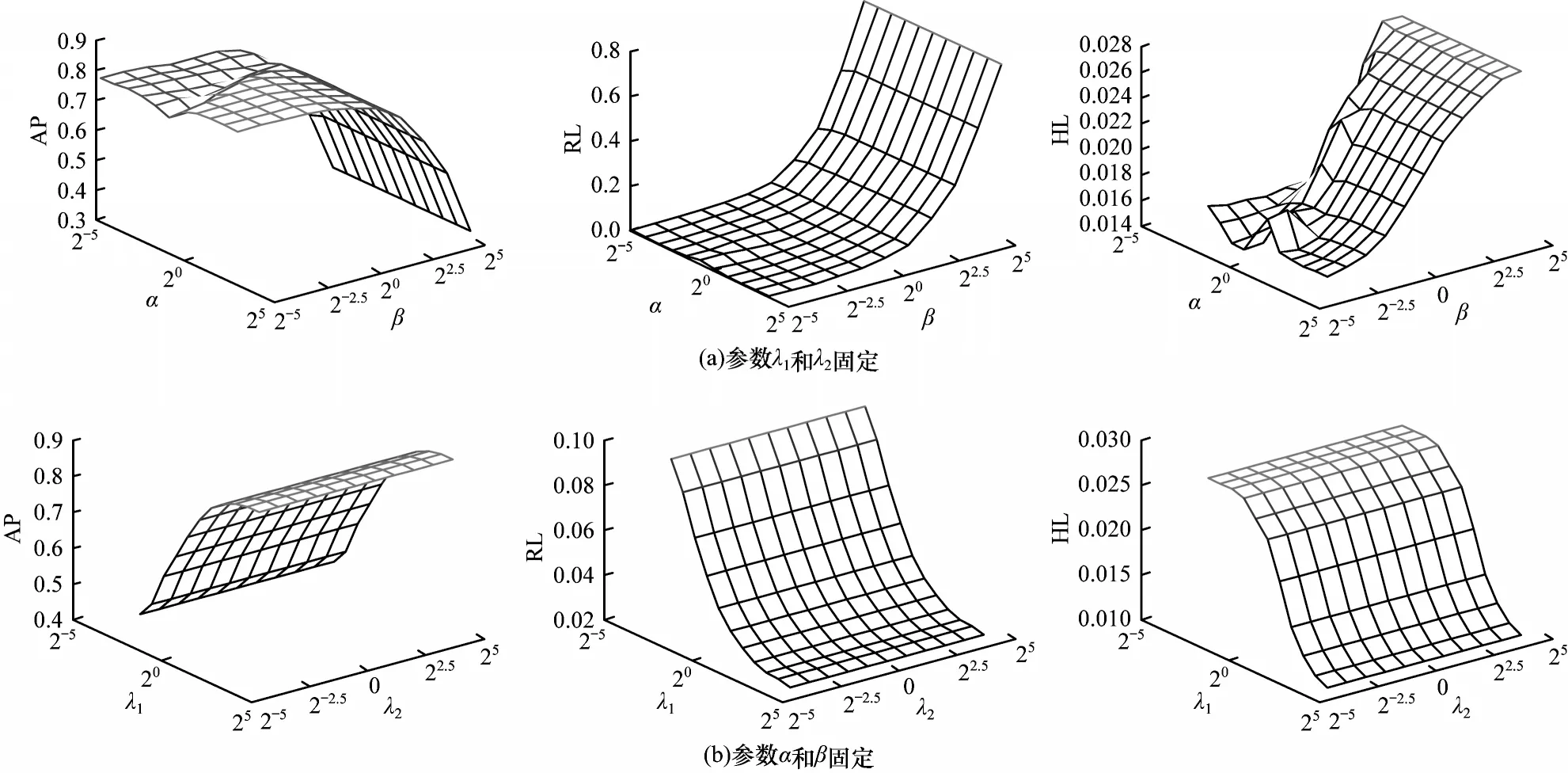
图2 MLDL 算法参数敏感性分析Fig.2 Parameter sensitivity analysis of MLDL algorithm
3.6 成分分析
为进一步验证所提的标签因果推断和双拉普拉斯正则化的有效性,本文对MLDL 算法进行成分分析实验,并在10 个数据集上进行额外实验。MLDL算法有3 个变体算法:1)只考虑因果推断和拉普拉斯正则化第1 项特征流形正则化的MLDL-L 算法;2)只考虑因果推断和拉普拉斯正则化第2 项标签流形正则的MLDL-F 算法;3)只考虑双拉普拉斯正则化的MLDL-C 算法。图3 所示为在10 个数据集上MLDL 算法及其变体算法的评价指标对比。

图3 MLDL 算法及其变体算法的评价指标对比Fig.3 Comparison of evaluation indicators for MLDL algorithm and its variant algorithms
本文选取AUC、CV 和HL 作为评价指标,其中AUC 越高算法性能越好,其他均是值越小算法性能越好。从图3 可以看出,MLDL 算法在所有情况下都优于其他3 种变体算法,证明双拉普拉斯正则化和因果推断的有效性。此外,从图3(a)、图3(b)和图3(c)可以看出,在AUC、CV 和HL 评价指标上,MLDL 算法表现出最优的性能。因此,MLDL 算法的双拉普拉斯正则化和标签因果推断都提升模型的多标签分类性能,侧面反映MLDL 算法的有效性和竞争性。
3.7 收敛性分析
本节对MLDL 算法的收敛性进行分析实验。图4 所示为MLDL 算法在Medical 和Arts 数据集上的收敛曲线。从图4 可以看出,MLDL 算法在迭代70 次左右呈现收敛趋势。此外,在其他数据集上也都在迭代70 次左右收敛。因此,在实验中采用的公开数据集上MLDL 算法都能快速收敛。
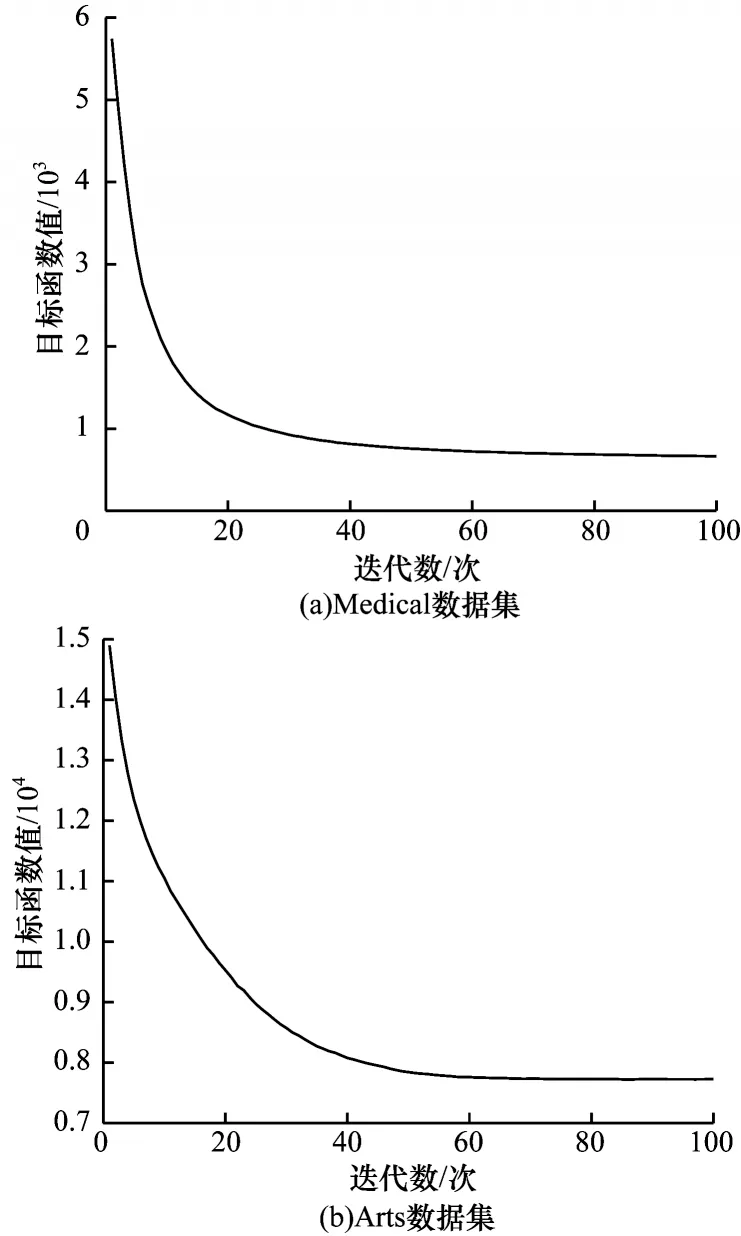
图4 MLDL 算法的收敛性分析Fig.4 Convergence analysis of MLDL algorithm
4 结束语
本文提出一种基于双拉普拉斯正则化和因果推断的多标签学习算法。在统一的线性多标签分类模型框架下,引入双拉普拉斯正则化有效地保持原始数据的局部流形结构,加入因果推断深入挖掘标签潜在的内在联系。通过线性回归方法建立多标签学习的基本框架,加入因果推断深入探讨标签之间的相互关系,最后引入双拉普拉斯正则化保持原始特征数据的局部流形结构。实验结果表明,相比多个主流算法,该算法性能表现更佳。由于加入双拉普拉斯正则化只是保持原始数据的局部流形结构,因此下一步将利用双拉普拉斯正则化进行局部和全局标签关系的结合。
