基于深度生成模型的聚合查询区间估计方法
2023-11-18薛晓东周云亮
房 俊,薛晓东,周云亮
(1.北方工业大学 信息学院,北京 100144;2.大规模流数据集成与分析技术北京市重点实验室,北京 100144)
0 概述
当前,用户希望通过对大数据的分析处理来发掘潜藏在数据间的关系,以获得更多有价值的信息。但是,由于数据量大的特性,传统的精确査询方法难以满足用户在访问效率上的需求。此外,部分用户所提出的分析需求可以理解为目的性不够明确的探索式査询,其特点是用户对结果准确性的要求并非十分严格,更在意查询速度是否足够快。近似查询处理(Approximate Query Processing,AQP)技术通常以远小于精确查询的查询代价为用户提供近似答案,往往允许用户在准确性和查询执行速度之间进行权衡。在数据探索式和可视化分析等应用中,这种权衡不仅可以接受,而且通常是有必要的。
目前,已经有不少学者对AQP 相关技术进行了研究,不同的方法在查询准确性、响应时间、空间预算和所支持的查询[1-2]之间进行了不同的权衡,要综合考虑这些方面来达成一个令人满意的方法仍然是一个挑战。基于抽样的AQP 是应用最广泛的近似查询处理方法之一,主要分为离线抽样和在线抽样两种。离线抽样意味着在查询开始执行之前创建样本。均匀抽样以等概率选择每个数据作为样本,虽然做法简单,但是在面对查询答案涉及多个值的分组查询时,随机抽样的方法很难为所有组提供足够准确的估计。分层抽样[3-4]是提高抽样精度的一种方法,它以不同的概率从每一组中进行抽样,但是分层抽样通常依赖于一些先验知识,如样本分布等。在线抽样[1]是在查询出现后动态创建样本,可以为给定的查询谓词选择足够的样本,从而提高精度。但是,在线抽样的缺点也很明显,查询时抽样意味着需要经常访问原始数据集,会导致较高的查询时延,这在交互分析中是不可接受的[5]。
随着人工智能技术的发展,模型驱动的AQP 方法近年来受到了更多的关注,研究人员将数据查询处理和优化技术与人工智能中的机器学习、深度学习等技术相融合[6],取得了一定的研究成果:一类研究通过生成模型来生成数据样本,再基于样本进行近似查询处理,相比于抽样方法,其生成样本速度较快,且在查询准确性、普适性上具有一定优势;另一类研究直接使用机器学习模型快速预测查询结果,这类近似查询方法虽然可以取得令人满意的时间性能,但是查询结果的误差评价缺乏理论保障。
现有的模型驱动方法多数以一个估计值来回答查询,从数理统计的角度来讲,这种点估计的方法产生的结果总是会存在误差,在面向某些不稳定的生成模型[如生成对抗网络(Generative Adversarial Network,GAN)模型[7]]时,这种问题尤为明显。区间估计可以在一定程度上判断总体估计量的取值范围,相应地会提高精度。不仅如此,在一些数据分析的实际业务场景中,研究人员对于某个总体估计量的取值范围更感兴趣,相比于单一值的点估计,采用置信区间作为返回值可以获得更多的数据分布特征。例如,将基于随机抽样方法得到的样本数据[{“id”:1;“pm25”:129},{“id”:2;“pm25”:138},{“id”:3;“pm25”:140},{“id”:4;“pm25”:90}]记为表T,针对查询“select avg(pm25)from T”(实际值是98.61),其点估计结果是124.25,使用区间估计方法Bootstrap[1]的计算 结果 是[104.2-7.04,104.2+7.04](置信度是90%),可以看出区间估计方法的估计值更接近实际值。
以中心极限定理及Bootstrap 方法为代表的相关技术为基于抽样的近似查询结果提供了误差范围保障。GAN 模型可快速生成多个样本,但是这些样本不满足中心极限定理的前提要求,一个猜想是是否可以通过多个样本查询结果来生成一个相对可靠的区间结果?此时,多个样本查询可能带来更大的查询时延,这也是Bootstrap 方法很少实际应用于AQP系统的主要原因。本文认为,当前分布式处理技术飞速发展,将相关技术引入AQP 系统中,有助于缓解上述性能问题。基于该思路,本文提出一种基于深度生成模型的聚合查询区间估计方法,目的是为给定查询生成足够样本以提高估计精度。首先利用深度生成模型学习数据分布特征,然后利用训练好的模型快速生成多个样本,随后通过基于抽样的AQP 方法为给定的查询任务计算估计值,最后计算相应的置信区间并返回给用户。
1 相关工作
近似查询处理的主要目标是高效地找到与精确答案接近的近似答案,多年来一直是数据管理领域研究的热点问题。基于抽样的AQP 方法由于效率和普遍性方面的优势而得到广泛的研究和应用。基于少量样本的查询响应速度很快,但是降低了准确性。很多研究人员都在寻找合适的样本,以期在不降低查询速度的情况下提高查询精度。随机抽样的查询方法的主要缺点是查询精度会随着聚合属性值方差的增大而降低,即随机抽样不能为具有高倾斜分布的数据集提供足够准确的估计。分层抽样是解决这一问题的一种方法,分层抽样虽然可以提高精度,但是通常需要一些有关数据分布的知识。国会抽样[3]是一种经典的分层抽样方法,其将每个组在总体中所占的频数作为依据,把原始数据分为若干组,在总体样本量确定的情况下,在不同组中利用随机抽样方法得到一定量的分样本,最后由分样本组成总体样本。CVOPT[4]是一种新的分层抽样方法,它根据变异系数分配各组的样本量。在线抽样[8-9]是AQP 的另一种方式,它以不断迭代的方式获得更多的样本,以提高估计精度,但是在线抽样需要在查询时抽取样本,会造成较高的查询时延。
有一些预计算的方法在执行查询之前根据查询工作负载计算直方图[10]、小波[11]、数据立方体等概要,从而快速获取聚合查询结果,但是这些方法不能支持通用的查询。此外,还有一些将抽样与预计算相融合的AQP 技术,如文献[12]提出了联合基于预计算的数据立方体和基于抽样的AQP 的AQP++技术,从而估计查询结果。
近年来,机器学习方法被广泛应用于数据处理和数据分析领域,有一些新的AQP 方法采用了机器学习技术。DBEst[13]是一种基于模型预测的AQP方法,它根据数据样本建立概率密度模型和回归模型,然后使用模型来直接回答查询。但是,对于分组查询,DBEst 需要为每个分组都构建一个模型,这将大幅增加模型训练和存储成本。文献[14]对DBEst 进行拓展,基于单词嵌入模型与神经网络的混合架构,使用轻量级模型降低了内存的占用率。LAQP[15]是一个融合基于抽样的AQP、预计算方法和机器学习的AQP 方法,其通过一个小的离线样本来获得较高精度的查询估计值。使用机器学习方法来获得近似查询结果的主要问题是目前还无法像基于抽样的AQP 方法那样提供误差保障。
还有一些基于模型样本的查询方法致力于使用深度生成模型来学习数据分布,通过模型生成样本然后回答查询。文献[16-17]提出一种使用深度生成模型学习数据分布并通过训练好的模型来生成样本以近似回答查询的方法,虽然该方法减少了查询延迟,但是仍然会受到抽样误差的影响。文献[18]训练一个基于工作负载的模型,该模型捕获数据的联合概率分布并反映其关键特征,也支持直接更新,即模型可以识别数据库上的操作类型,无需重新训练模型。
在大多数抽样估计方法中,置信区间被广泛用于评价近似查询的估计结果[19],通常根据用户给定的置信度计算一个相应的置信区间。如果数据集的数据分布是已知的,或者有一个足够大的样本来得到数据分布,则上述过程转变为一个经典的统计问题——参数估计。以计算一个正态分布上的某一属性均值为例,如果已知正态分布的方差,则可以很容易地使用高斯分布模型N(µ,σ2)来计算置信区间。如果方差是未知的,可以将其形式化为T 分布。如果数据分布是未知的,则可以通过Bootstrap 和Closed-form Estimate[20]两种方 法。Bootstrap 旨在获得多个样本,对于每个样本S,可以计算出一个估计值,由这些值组成的分布可用于估计总体聚合结果的值。Bootstrap 对数据分布没有限制,适用于大多数查询,但是大多数Bootstrap 方法需要数千次重采样,而重采样过程非常耗时,因此Bootstrap 在实际应用中很受限制。Closed-form Estimate 方法以正态分布N(θ(S),σ2)来近似抽样分布,并通过样本的特殊封闭函数Var(S)估计方差σ2,利用中心极限定理可以证明这种近似的合理性。然而,Closed-form Estimate 方法只能适用于COUNT、SUM、AVG 这类比较容易计算方差的查询。
2 方法介绍
如图1 所示,本文基于深度生成模型的聚合查询区间估计方法主要分为3 个阶段:利用预处理后的数据训练深度生成模型,经过多次迭代训练后得到可靠的数据生成模型;基于该模型生成多个数据样本,等待用户查询;用户查询到来后在不同样本上分别执行查询,将全部查询结果汇总,根据用户给定的置信水平计算相应的查询结果置信区间并返回给用户。

图1 近似查询方法执行过程Fig.1 The execution process of approximate query method
2.1 CWGAN-GP 模型训练
在模型训练阶段,本文使用深度生成模型CWGAN-GP 来生成样本,CWGAN-GP 是WGANGP[21]和条件生成对抗网络(Conditional Generative Adversarial Network,CGAN)[22]的组合网络。
GAN 模型的核心思想是用训练神经网络来代替对似然函数的求解,利用生成器和判别器之间的对抗学习来不断优化模型的参数,利用这种方法规避求解似然函数的问题。但是,GAN 模型还存在一些问题,如模型难以训练等。WGAN(Wasserstein GAN)[23]从原理上说明了GAN 模型存在的缺陷,提出用Wasserstein 距离替代KL 散度和JS 散度,优化了生成器和判别器的目标函数,因此,在很大程度上缓解了原始GAN 模型存在的一些问题。但是,WGAN 在训练过程中常会出现收敛速度慢、梯度爆炸等现象。WGAN-GP 将判别器的梯度作为正则项加入判别器的目标函数中,该正则项通过梯度惩罚使判别器梯度在充分训练后稳定在Lipschitz 常数附近。经过优化,WGAN-GP 几乎不再出现梯度消失或梯度爆炸的问题,在很大程度上提高了模型收敛速度。CGAN 模型是GAN 模型的扩展,它向GAN的生成器和判别器添加条件设置,可以在给定条件下生成相应的数据。
CWGAN-GP 模型训练过程如图2 所示,将真实数据x及其对应的标签y提供给模型,训练生成器G和判别器D。首先固定G,训练D,这是一个二分类问题,即给定一个样本,训练D 判断其是真样本还是由G 生成的假样本;之后固定D,训练G,给G 一个随机输入,损失函数是D 的输出结果,根据损失函数对G 的参数进行更新。重复上述2 个过程,经过多次训练后,生成器与判别器达到纳什均衡就停止,此时生成器可以为给定的标签生成一个与真实样本x相似的样本x′。

图2 CWGAN-GP 模型训练过程Fig.2 Training process of CWGAN-GP model
在模型训练前需要标记数据,为使模型能够为给定的组生成样本,本文用组属性值来标记数据,编码的分组属性值将被视为训练数据的标签。一些研究人员[16-17]使用One-Hot 编码方法来实现,假设属性A有3 个取值{A1,A2,A3},One-Hot 编码为A1=001,A2=010,A3=100。如果属性域取值较多,这种方法会导致2 个主要问题:编码后的向量可能非常稀疏,导致性能较差[24];提高了模型学习的参数量,增加了模型的训练时间。针对这些问题,本文使用Binary-Encoding来降低编码维度,同时使得编码后的向量更加稠密。上述例子使用Binary-Encoding编码后,只需要二维向量(「lb 3⏋=2),编码结果为A1=00,A2=01,A3=10。
2.2 多样本生成
如图3 所示,基于大规模并行处理(Massively Parallel Processing,MPP)[25-26]架构快速生成多份样本,该架构包括Master和Segment两类服务器节点。

图3 基于MPP 的多样本生成与近似聚合查询Fig.3 Multi sample generation and approximate aggregation query based on MPP
Master 节点主要负责:
1)将第2.1 节的CWGAN-GP 生成模型复制到Segment 节点的模型存储库
2)维护聚合查询的生成模型映射元数据
3)接收Client的多样本生成请求(qPattern,n,m),其中,n为生成的样本份数,m为每份样本的数据量。形成分布式生成样本的任务请求(mID,ni,m)并分配给Segment 节点,其中,mID 是qPattern 对应的模型主键,ni是第i个Segment节点需要生成的样本个数,ni根据Segment节点数量采用均衡策略生成。
Segment 节点主要负责:
1)接收并存储数据生成模型。
2)接收Master节点的生成样本请求(mID,ni,m),使用相应的CWGAN-GP 生成模型生成样本。
为了能够有效利用物理资源,每个多核Segment节点可并行执行多个任务实例。在每个Segment 节点上开启多个进程,并行生成样本,之后将样本放到Segment 节点的样本内存区域。
分组查询的结果涉及多个值,随机抽样方法很难为所有组提供足够准确的估计。为提高准确性,本文选择用分层抽样的方法获取每份样本,算法1描述了使用生成器G 生成样本的过程。根据数据集中各分组属性在总体中所占的比例来计算样本中每组的个 数NSamplesize。Random(z,NSamplesize)表示产 生NSamplesize个随机噪声,将其作为模型的输入。Repeat(Binary-Encoding(i),NSamplesize)表示重复得到NSamplesize个经过Binary-Encoding 编码的标签数据,作为模型的输入。
算法1模型生成样本的过程
2.3 聚合查询区间估计
聚合查询区间估计阶段仍然基于图3 的MPP 架构来完成。由Master 节点将聚合查询任务并行分发到各个Segment 处理节点,每个处理节点开启多个进程,每个进程负责完成一个查询子任务,生成一个近似查询结果,并回传给Master 节点。在每个节点都完成查询任务后,Master 节点将n个近似查询结果汇总并计算得到最终的结果。借助中心极限定理,以正态近似的方式来计算置信区间,最终得置信区间为其中:Mean(S)表示n份样本集上聚合结果的均值;Var(S)是聚合结果的方差;a是用户给定的置信水平为分位数。
3 实验验证
3.1 实验环境
本文实验中的查询任务是在集群上完成的,集群由6 台同配置服务器组成,配置如表1 所示。其中,1 台服务器用于模型训练及Master 节点,其余5 台服务器作为Segment 节点用于样本生成和查询处理。为了充分利用物理资源,每个多核Segment节点可并行执行多个任务实例,在本次实验中,每台服务器设置16 个进程。

表1 实验环境Table 1 Experimental environment
3.2 实验数据
本文分别在如下2 个数据集上进行实验:
1)PM2.5[13]数据集,包含了美国驻北京大使馆的pm25 数据信息,同时还包括了北京首都国际机场的气象数据,共43 824 条数据。在对PM2.5 数据集的聚合查询中,聚合值属性是“pm25”,且每个谓词只涉及一个属性“PREC”,其余部分属性如表2所示。
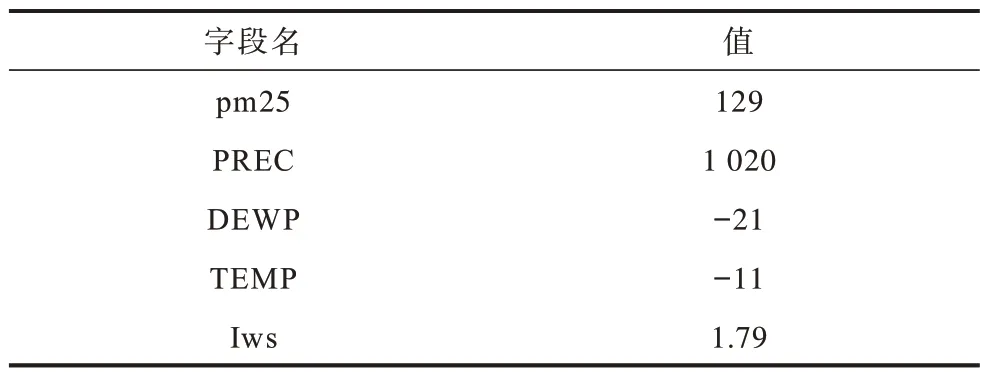
表2 PM2.5 数据Table 2 PM2.5 data
2)ROAD[16]数据集,这是一个为道路网络添加海拔信息而建造的数据集,共包含434 874 条数据。ROAD 数据集 有“Longitude”“Latitude”和“Elevation”3 个属性。本文在ROAD 数据集上添加一个按组排列的属性“GroupID”,并将“Latitude”的取值范围划分为10 个相等的子范围,每条数据添加的组属性值是其所属子范围的索引。修改后的数据集有4 个属性,如表3 所示。

表3 ROAD 数据Table 3 ROAD data
本文实验用到的查询包括带谓词的查询以及分组查询,聚合函数有COUNT、AVG。部分查询语句如表4 所示。

表4 查询语句Table 4 Query statements
3.3 评价指标
本文采用置信区间的覆盖率(Confidence Interval Coverage,CIC)来衡量查询估计的准确性。CIC 是利用本文方法计算置信区间后统计给定查询的实际值落在置信区间中的比例,计算公式如下:
其中:Result 是在原始数据集上执行查询的结果集;truei表示第i组的真实聚合值,是集合Result 中的元素;Interval 为计算的置信区间;d(x,y)是一个判别函数,若实际值x落在置信区间y中,则取值为1,否则取值为0。
为了对比不同置信区间的计算结果,将CIC 进行归一化,即计算CIC 与相应置信度a的比值,如式(2)所示:
3.4 结果分析
本文生成模型CWGAN-GP 的生成器有4 个全连接的隐藏层,每层中神经元的数量分别为512、256、128、64 个。判别器有3 个全连接的隐藏层,每层中神经元的数量分别为512、256、128 个。将优化器设置为RMSprop,设置RMSprop 的参数为(lr=0.000 05,rho=0.95)。在计算置信区间时,增加每份样本集的数量会对计算结果产生影响,但同时也需要考虑性能,在本节实验中会比较不同样本集数量下的结果,从而选择合适的取值。设置抽样轮次r=103,实验结果均为经过多次实验后所得。
3.4.1 深度生成模型的抽样效率
本次实验基于ROAD 数据集,比较利用模型生成样本和利用随机抽样方法生成样本所耗费的时间。为了比较不同数据规模下的抽样效率,首先利用ROAD 数据集 生成大 小依次 为1×106、10×106、50×106、100×106、200×106的5 个实验数据集,再分别从这5 个实验数据集中利用随机抽样方法抽取1 000 个数据作为生成样本,实验结果如图4 所示。从图4 可以看出,利用模型生成样本所需的时间小于随机抽样方法,且前者所需的时间与数据集大小无关。随机抽样方法的抽样时间与数据集大小呈线性相关,随着数据集的增大而不断增加。可见,利用模型生成样本的方法对于大数据集将更加有效。

图4 数据集大小对抽样时间的影响Fig.4 The impact of dataset size on sampling time
3.4.2 深度生成模型的抽样效果
本次实验将在ROAD 和PM2.5 数据集上分别对生成样本和随机样本的分布进行可视化。从每个数据集中选择1 000 个随机样本,同样地,利用模型也生成1 000 个样本。为了更加准确地表示数据集的数据分布,以分层抽样的方法获得随机样本,即根据数据集中不同分组中的元组数量来分配样本集中这一分组的数量。图5 分别显示了在2 个数据集中随机样本和生成样本的分布情况。从图5 可以看出,生成样本和真实样本的分布在视觉上比较相似,即由模型生成的样本数据比较接近数据集中的真实数据,因此,可以由模型生成的样本来代替从数据集中抽样获得的样本。

图5 样本分布对比Fig.5 Sample distribution comparison
3.4.3 置信区间的覆盖率
通过改变查询谓词范围生成查询数量分别为100、200、300、400、500 个的任务集。利用本文方法计算置信度分别为80%、85%、90%、95%的置信区间,在2 个数据集上对比计算所得归一化的置信区间覆盖率(NCIC),结果如图6 所示。由图6 可知,由本文方法得到的查询结果计算的NCIC 均可达85%以上,其中有48.25%的任务集计算的NCIC 在95%以上,这表明区间估计结果具有较高的精度,而且在不同数据集、面对不同查询任务时均有较好的表现,可移植性高。
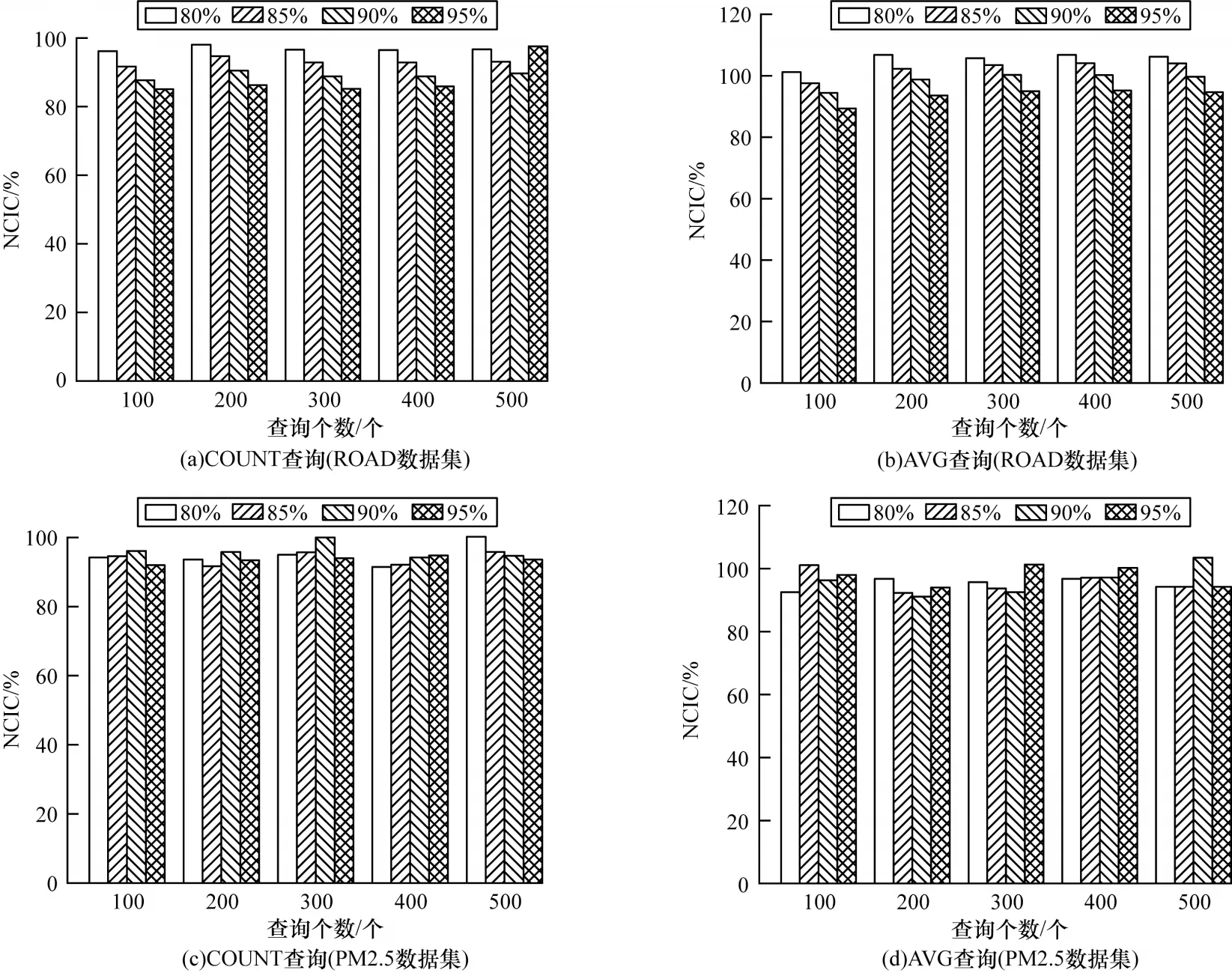
图6 归一化的置信区间覆盖率对比Fig.6 Comparison of NCIC
3.4.4 查询时间对比
将本文方法与第1 节中提到的几种常见查询方法进行对比,包括随机抽样的查询方法、基于模型样本的查询方法、基于模型预测的查询方法,分析各方法执行查询所需的时间。其中,基于模型样本与基于随机抽样的查询方法的时间相同,因此没有列出基于模型样本的方法的结果。在PM2.5 数据集上,生成抽样比分别为5%、10%、15%、20%、25%、30%的样本,对比执行查询所需的时间,在接下来的实验中,未加特别说明时均计算置信度为90%的置信区间,实验结果如图7 所示。由图7 可知,本文方法在查询时间上开销大于基准方法,主要原因是本文方法涉及在多份样本上执行查询,之后还需要汇总查询结果生成区间结果,这一过程比较耗时,但从整体来看,秒级时间开销对于常规应用还是能够接受的。

图7 查询时间对比Fig.7 Query time comparison
3.4.5 样本量对查询结果的影响
设置300 个聚合函数为COUNT 的查询来比较不同样本量对查询结果的影响。本文主要考虑执行查询所需时间和置信区间的覆盖率CIC,结果如图8所示。

图8 样本量对查询结果的影响Fig.8 The impact of sample size on query results
由图8 可以看出,随着样本量的增加,查询的执行时间不断增加,而置信区间的覆盖率增长率逐渐减少,即曲线逐渐变得平稳。综合比较来看,对于ROAD 数据集,本文选择样本量n=100,对于PM2.5数据集,选择n=80。
3.4.6 查询选择性对查询结果的影响
在ROAD 和PM2.5 数据集上分别测试查询选择性对查询结果的影响,设置300 个聚合函数为COUNT 且选择性低于0.03 的查询,对比随机样本与生成样本的置信区间覆盖率,结果如图9 所示。

图9 查询选择性对结果的影响Fig.9 The impact of query selectivity on results
从图9 可以看出,对于随机样本和生成样本,置信区间覆盖率都随着查询选择性的增加而增加,并且基于生成样本的估计更加准确。其原因是:与从整个数据集中选择的随机样本相比,生成样本所包含的满足查询谓词的样本比例更高。本实验中的查询是低选择性的查询,这意味着从整个数据集中选择的大多数样本不满足查询谓词,只有一小部分样本对估计有贡献,这导致随机样本的精度较低。由于生成模型可以灵活地生成某些子范围的样本,因此可以获得更多的样本,有助于提高估计精度。
4 结束语
本文提出一种基于深度生成模型的聚合查询区间估计方法。该方法在不访问原始数据集的条件下,利用CWGAN-GP 模型为给定的查询并行生成多个近似样本,通过多个样本查询结果聚合生成相对可靠的区间查询结果。实验结果表明,相比于常见的点估计近似查询方法,该方法不仅提高了近似查询估计的精度,也能够降低查询误差。此外,该方法还可以根据不同的优化目标与多种抽样方法相结合。虽然本文方法取得了较好的结果,但是生成大量的样本客观上也增加了时间开销,因此,下一步将继续优化抽样以及查询过程,减少时间开销。此外,根据查询结果日志来判断生成样本的质量,有选择性地替换部分样本集,进一步提高查询精度,也是今后的研究方向。
