基于深度学习的LBlock安全性分析及其应用

杨小东 李锴彬 杜小妮 梁丽芳 贾美纯

①(西北师范大学计算机科学与工程学院 兰州 730070)

②(桂林电子科技大学广西密码学与信息安全重点实验室 桂林 541004)

③(西北师范大学数学与统计学院 兰州 730070)

④(西北师范大学密码技术与数据分析重点实验室 兰州 730070)

1 引言

近年来，伴随无线传感器网络以及射频识别技术(Radio Frequency IDentification,RFID)的发展和广泛应用，对资源受限的设备进行数据加密需要使用轻量级分组密码算法。然而轻量级分组密码算法追求低功耗与高效率并存，这一矛盾会导致算法的安全性无法得到保证，针对这一问题目前还没有较好的解决方案，因此有必要对这些轻量级分组密码算法的安全性做进一步分析。

轻量级分组密码安全性分析的关键在于构造一个有效的区分器，即按照算法的结构或其部件的特征将密码算法和随机数据区分开。Biham等人[1]提出的差分区分器是对分组密码攻击最有效的工具之一。近年来，随着云计算和大数据的快速发展，深度学习技术在语音识别、自然语言处理和生物特征提取等领域具有广泛的应用。该技术在对固定微弱特征的发现识别中具有较强的能力，因此密码研究人员尝试将深度学习技术应用到分组密码的安全性分析中。2011年，Hospodar等人[2]通过深度学习技术对高级加密标准(Advanced Encryption Standard,AES)[3]进行侧信道攻击，该攻击的效果很大程度取决于模型超参数的选取。2012年，针对DES和T rip le-DES,A lani[4]提出了基于神经网络的已知明文攻击，该攻击可以直接从密文中恢复出明文。2018年，Hu等人[5]使用反向传播网络对AES进行密码分析，该网络在密钥未知的情况下可以从密文中还原出明文，试图达到全局推演的效果。随后在2019年的美密会上，Gohr[6]提出了基于深度学习的减轮Speck32/64改进差分攻击，通过训练卷积神经网络来区分固定输入差分的密码算法和随机数据，展示了将深度学习技术用于分组密码分析的可行性。2021年Benam ira等人[7]在欧密会上，对Gohr区分器的构造原理做了进一步研究，并为机器学习辅助分组密码的安全性分析开辟了一个新方向。同年Su等人[8,9]采用PU学习(Positive-Unlabeled learn ing)对减轮Speck32/64构造了5轮和6轮的区分器，与Goh r构造的区分器相比具有更高的精度。Hou等人[10]受Benam ira等人的启发，将输出差分拼接到矩阵上进行区分器的训练，提高了区分器的识别轮数和精度。Chen等人[11]提出了用于密码分析的神经网络辅助统计攻击方式，该攻击方式将区分器的应用范围首次从实际攻击扩展到了理论攻击，从而有效提高了区分器的精度。2022年，Baksi[12]等人将区分器的构造问题转化为神经网络的分类问题，以便神经网络对数据进行有效管理，并将神经网络应用于流密码，扩展了深度学习技术在密码技术的适用范围。

LB lock算法[13]是在2011年ANCS(A rchitectures for Networking and Comm unications System s)会议上提出的一种Feistel结构的轻量级分组密码，具有优良的软硬件实现效率。该算法能够满足RFID设备低功耗高性能的需求，且适用于物联网(Internet O f Things,IOT)设备的安全性，可在16 bit处理器上高效执行。算法提出以来受到了国内外学者的广泛关注，先前研究者针对LBlock算法的安全性分析主要致力于传统密码分析，包括相关密钥不可能差分分析[14]、相关密钥线性分析[15]零相关线性分析、积分分析和侧信道立方分析等多种密码分析方法，现有的研究结果表明，LBlock算法具有很好的安全性。虽然针对该算法的攻击方法很多，但大多都是理论攻击。针对LB lock算法，文献[14,15]给出了实际的密钥恢复攻击结果，但数据复杂度和时间复杂度较高，且实现步骤较为复杂。

受Gohr[6]方法的启发，本文通过固定不同的输入差分，构造了基于深度学习的减轮LBlock差分区分器，并利用该区分器进行了密钥恢复攻击。本文的主要贡献包括2个方面：

(1)基于残差网络，构造了基于深度学习的减轮LBlock差分区分器，其中7轮和8轮区分器模型的精度分别是0.999和0.946。这是对LB lock算法安全性分析的全新思路，与传统区分器相比具有更好的普适性和可实现性。

(2)数据复杂度和时间复杂度是衡量攻击实现效率的重要指标，其值越小实现效率越高。本文利用9轮区分器对11轮的LBlock进行了密钥恢复攻击，该方案大幅降低了所需的数据复杂度和时间复杂度，分别为223.41和 229.03，且实现效率更高，表1给出了该方案与已有攻击方案的对比。同时，该攻击方案可以将正确子密钥限定在较小范围内，结果更准确。相比传统方案，在构建密钥恢复攻击所需的r-1轮区分器时流程简单，且易于使用。

本文第2节简要介绍了LB lock密码算法、差分区分器和残差网络等基础知识；第3节给出了基于残差网络构建的减轮LBlock差分区分器，并给出了区分器的训练结果；第4节提出了基于神经网络区分器的密钥恢复攻击方案，并对减轮LBlock算法进行了密钥恢复攻击实验；第5节总结了本文的工作，并对后续的研究进行展望。

2 预备知识

2.1 LBlock加密算法

轻量级分组密码LBlock为两路Feistel结构，分组长度为64 bit，密钥长度为80 bit，加密轮数为32轮，加密结构如图1(a)所示。轮函数F包括轮密钥加、S盒变换和扩散变换P，F的结构如图1(b)所示。LB lock算法在S盒变换中使用了8个完全不同的4 bitS盒，扩散变换P为4 bit块之间的位置变换。设明文M=X0||X1，当1≤i≤31时，第i轮的输入记为(X i-1,X i)，其中X i+1=F(X i,K i)⊕(X i-1＜＜＜8)，(X i,X i+1)为 第i轮 的输出，当i=32时，(X32,X33)为第32轮输出。算法各个模块部分定义如下，其中S盒的真值表与密钥扩展算法的详细流程见参考文献[13]。

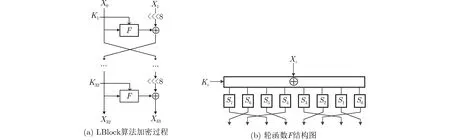
图1 LB lock分组密码算法

(1)轮函数F，结构如图1(b)所示

(3)扩散变换P

2.2 差分区分器

对{0,1}n上的随机置换π，任意给定差分(α,β),α=0,β=0，则差分概率约为1/2n。如果找到一条r-1 轮差分概率大于1/2n的差分特征，就可以将r-1轮密码算法与随机置换区分开。构建差分区分器的本质是寻找一条高概率的差分特征。

2.3 残差网络

2015年，He等人[16]在2015年的Im ageNet大规模视觉识别竞赛(Im agenet Large Scale Visual Recognition Challenge,ILSVRC)上提出残差网络。与卷积神经网络不同，残差网络加入了捷径连接来形成残差单元。它可将其中一层的激活值绕道传给更深层的网络，不但简化了学习目标，而且保护了信息的完整性。进一步残差网络也较好地解决了由网络层数增多引起的误差增高和梯度消失问题，从而加快了模型的训练速度，提高了训练效果。

3 减轮LBlock算法的神经网络区分器设计

深度学习技术能够很好地揭示数据中的隐含特征。利用寻找差分特征的思想将其转化为深度学习的二分类问题。本节的主要工作是基于残差网络来构建神经网络区分器，并给出了区分器的训练结果。

3.1 神经网络区分器的构造和设置

本部分将给出神经网络区分器的构造方法，并分别对区分器的数据集的生成过程、网络模型和激活参数等进行设置。

(1)数据集的生成过程：训练数据和验证数据均用L inux随机数生成器生成。从6组输入差分Δx(0x0/0xd,0x0/0x2 ,0x0/0x4,0x0/0x8 ,0×0/0×40 ,0x0/0x80)中选取1组，将随机生成的明文对记作(P0,P1)，在随机密钥情况下，用LB lock加密得到相应的密文对(C0,C1)，将上述过程生成的密文对设标签为0，记为负样本。将(P0,P1)与Δx进行异或运算得到，同样地通过LB lock加密得到密文对，将上述过程生成的密文对设标签为1，记为正样本。将负样本与正样本中的密文对合成为一个行向量，作为训练集和验证集的数据部分，记为，密文对与明文对(P0,P1),相 对应，并用Y表示标签的值。密文对左半部分和右半部分都可以写成4个16 bit的字(w0,w1,w2,w3)，反映了LBlock算法面向字结构的特点。在神经网络区分器的训练过程中，w i解释为128 bit的行向量。将wi通过Reshape函数转化为4×32的矩阵作为神经网络输入层的输入。训练集大小为 102，验证集大小为1 05，数据集选取5000作为一个批次训练。数据集中正负样本数量相等，呈均匀分布。

(2)网络模型：本文选择残差网络来训练神经网络区分器。网络模型包括3个主要部分：输入层、隐藏层和输出层，如图2所示。首先，由4 ×16 bit的训练数据构成的矩阵行向量作为网络的输入。其次在隐藏层中使用5个残差块的堆叠进行数据建模。每个残差块中，设置了两个卷积层，每个卷积层连接1个批量归一化层和1个激活函数。最后将隐藏层的数据展平后发送到一个全连接层得到输出结果，其中全连接层由隐藏层和输出单元组成。

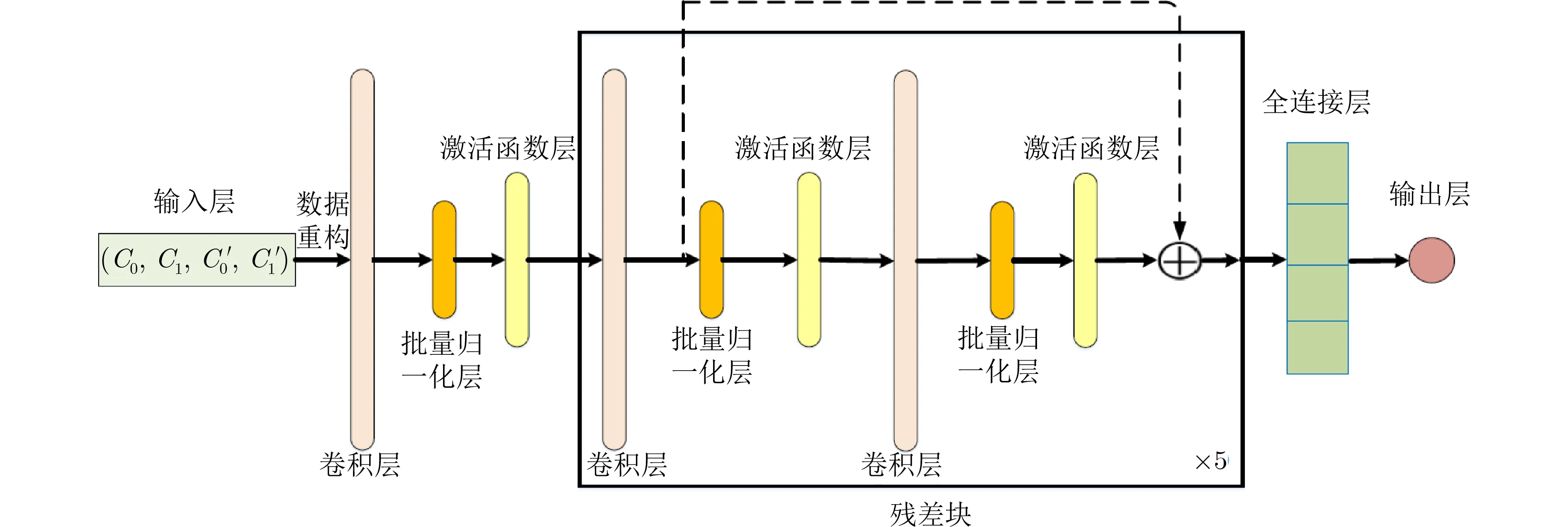
图2 残差网络区分器模型

隐藏层由残差块构成，其中第1个卷积层的内核大小为1，第2个卷积层的内核大小为3。此外，每个卷积层中的filter数量为64。最后基于L2权重正则化训练网络，以避免过度拟合，正则化参数为10-4。

(3)激活函数：sigm oid函数也称为Logistic函数，它可以将一个实数映射到(0,1)区间。本文神经网络的预测头中只有1个输出单元，所以，将该激活函数应用于输出层，其表达式为

(4)其他参数设置：使用Adam算法和Keras中的默认参数。将均方误差函数(Mean Square Error,MSE)作为损失函数。模型训练中调用ModelChenkpoint回调函数保存最佳模型。神经网络区分器的构造算法如算法1所示。

3.2 神经网络区分器的训练结果

实验平台的硬件环境为处理器：AMD EPYC 7302，内存：64 GB，显卡：NVIDIA GeForce RTX 3090，操作系统：Linux。深度学习库：Tensorflowgpu 2.5，前端Keras，采用GPU进行并行计算。

实验表明，采用算法1进行神经网络区分器的训练时，输入差分的汉明重量越大，密文对的非随机特征越弱。故本文选取6组汉明重量均为1的输入差分进行训练。图3、图4和图5分别给出了7～9轮中区分器性能最优的一组训练情况。其中横轴表示训练轮数(epoch)，纵轴表示区分器的精度或损失率。精度表示区分器正确分类的样本数与总样本数之比，该指标衡量了区分器的分类能力。由这3组图可以看出由于初始学习率值较大，损失率下降较快。随着算法迭代轮数增大，模型的学习率得到调整，精度增加，损失曲线也趋于稳定。特别地图3(a)中精度的变化反映出该模型能够选择出更多的密文对，从而寻找高概率差分对的能力也越强。同时在第7个epoch后精度接近1，这说明是一个近乎完美的7轮区分器。

图3 Δ x=0x0/0x4的7轮LB lock神经网络区分器的性能度量

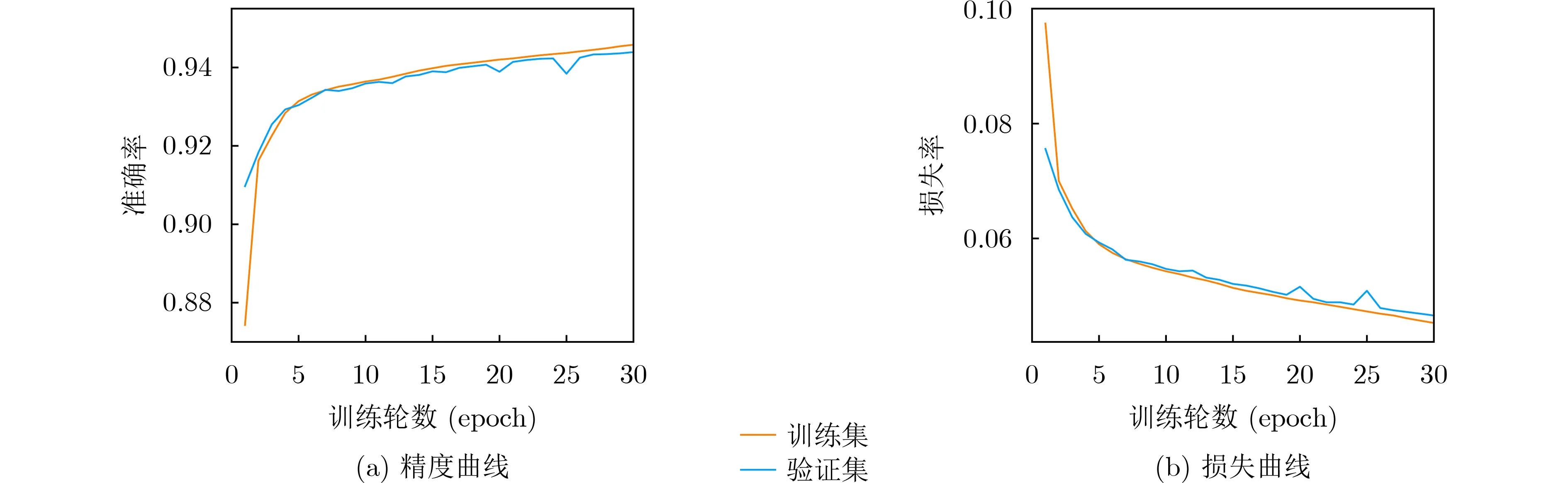
图4 Δ x=0x0/0x2的8轮LBlock神经网络区分器的性能度量

图5 Δ x=0x0/0x1的9轮LBlock神经网络区分器的性能度量

表2给出了LBlock 7～9轮神经网络区分器的精度、损失率和训练时间等性能指标。从表2可以看出随着密码迭代轮数和epoch的加大，模型的训练时间显著上升。随着密码迭代轮数的增加，精度下降，同时明密文之间的统计信息越弱，导致正负样本的相似性提高，使得深度学习难以进行有效的特征选择。通过延长epoch，8轮和9轮区分器的性能指标均出现了不同程度的上升。需要说明的是，在区分器的训练中通过调用EarlyStopping函数，使模型提早结束了训练，从而减少了模型的训练时间。该函数通过计算模型在验证集上的性能表现来适时结束训练，当验证集上的性能表现开始下降时停止训练，从而避免模型的过拟合。

算法1 神经网络区分器的构造

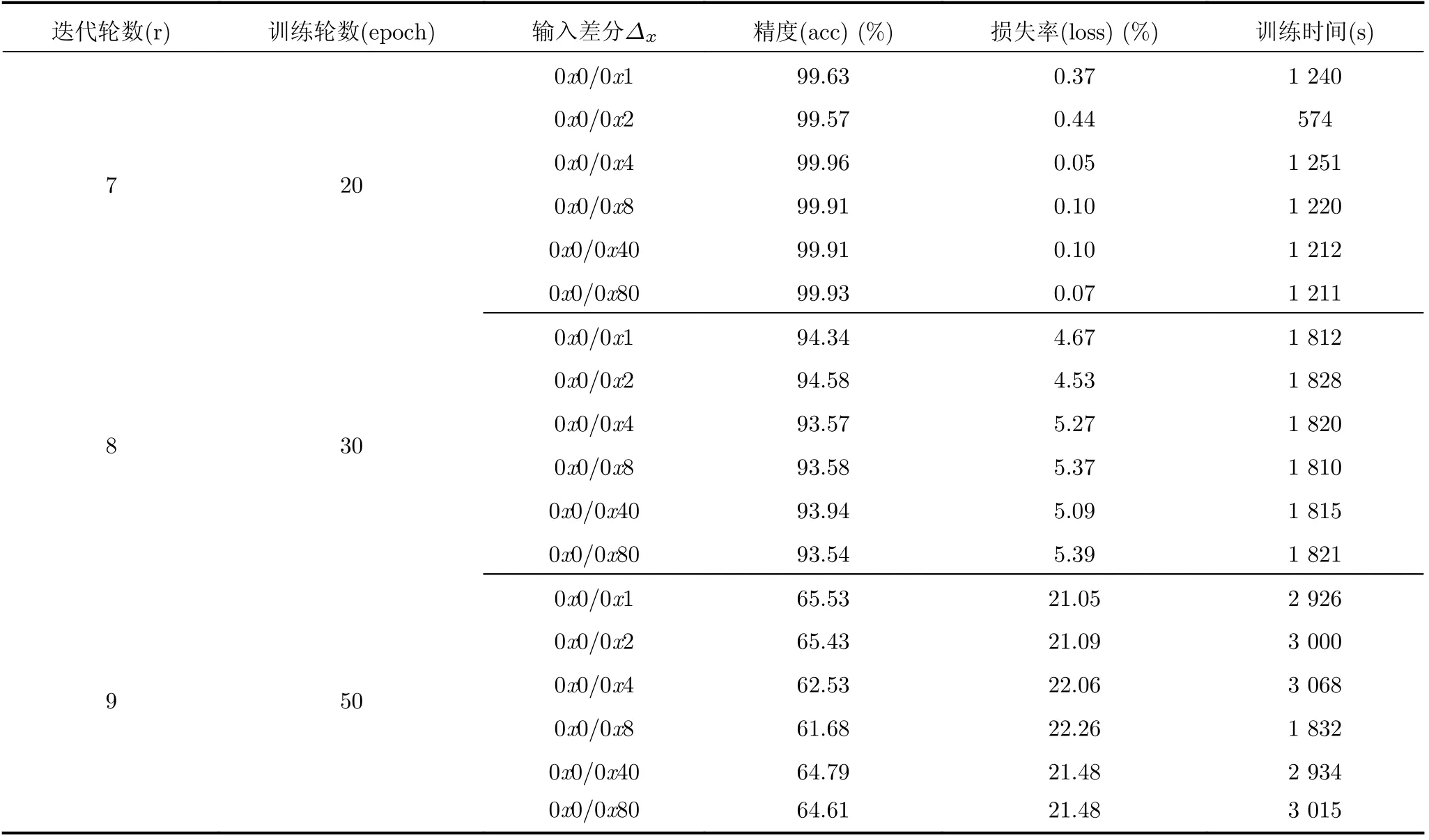
表2 LBlock 7～9轮区分器模型的性能指标

4 神经网络区分器的应用

本节给出了利用神经网络区分器进行密钥恢复攻击的方案，并给出了基于训练得到的9轮神经网络区分器对LBlock进行11轮密钥恢复攻击的结果。

4.1 密钥恢复攻击方案

采用算法1得到针对LB lock的r-1轮局部最优神经网络区分器，基于该区分器的密钥恢复攻击方案如算法2所示。

(1)随机生成明文(P0,P1)，固定输入差分Δx，使得=(P0,P1)⊕Δx。通过相同子密钥，使用LB lock加密得到密文对。随机生成131071个候选密钥，用于猜测密钥。其中输入差分Δx、训练集验证集的大小和训练批次的大小与算法1相同。

(2)使用所有候选密钥，对生成的密文对进行1轮解密，将得到的结果记为(X0,X1)。

(3)步骤(2)的输出(X0,X1)输 入到r-1轮区分器，得到每个候选密钥Key的概率，按概率将所有候选密钥降序排列。

4.2 密钥恢复攻击结果

根据LB lock的结构特点，将Δx=0x0/0x2的9轮区分器无损失地向上扩展1轮，再通过正确密钥加密1轮至11轮。利用算法2对11轮LBlock算法的所有候选密钥进行筛选。采样点值ωi=model(X0,X1)，其中(X0,X1)为通过末轮密钥解密得到的密文对。差分为Δ的错误密钥均值分布如图6所示，其中横轴表示密钥数量，纵轴表示区分器输出的错误密钥均值，概率在49.68%～58.20%。训练集包含1 07个样本，验证集包含1 05个样本，故训练每个区分器共需加密1 07+105=107.04次。采用4 096个选择明密文对，该攻击的时间复杂度为107.04+212×217≈229.03。

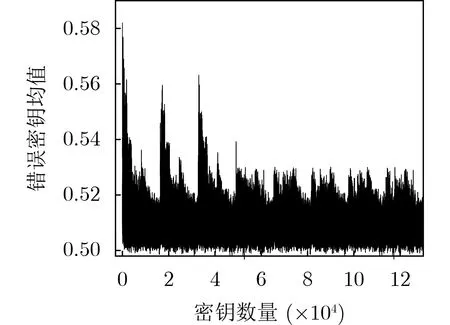
图6 LB lock11轮密钥恢复攻击错误密钥均值分布

4.3 与传统方案的比较

Zhou等人[17]采用混合整数线性规划(M ixed-Integer Linear Programm ing,M ILP)给出了LB lock的16轮差分轨迹，其中9～11轮的差分传播概率分别为2-28,2-36和2-44，所需的数据复杂度分别为228, 236和 244。而利用本文区分器进行11轮攻击，所需数据复杂度仅为107+106+212+217=223.41。本文分别采用文献[14,15]方案与本文方案对11轮LBlock进行了密钥恢复攻击，数据复杂度和时间复杂度的对比如表1所示，可以看出本文方案的以上性能指标均优于传统方案。但随着密码算法迭代轮数的上升，神经网络难以从数据中提取到有效特征，相比传统方案在算法攻击轮数上仍有差距。

5 结束语

本文基于残差网络，构建了针对减轮LBlock算法的神经网络区分器，并利用该区分器进行了密钥恢复攻击。实验结果表明，对于7轮和8轮的LBlock算法，通过固定不同的输入差分可得到较高精度的区分器，其中通过调用EarlyStopping函数得到的7轮区分器近乎完美，并有效防止过拟合现象的出现。与传统密钥恢复攻击方案相比，基于神经网络区分器的方案在数据复杂度和时间复杂度上均有效降低。而且将神经网络和传统差分密码分析相结合的思路，对其他减轮轻量级分组密码的安全性分析具有潜在优势。不可否认，影响神经区分器性能的因素有很多，比如本文讨论的数据格式、网络结构、模型训练方法等。将来的工作将探索从多个维度提高神经网络区分器性能的方法对LBlock算法的更高轮数进行攻击。此外，能否利用深度学习的其他算法构建性能更优的区分器仍需进一步研究。