基于时隙变换的多用户多载波相关延迟移位键控系统
2023-11-18李超凡蒋忠均
张 刚 李超凡 蒋忠均
①(重庆邮电大学通信与信息工程学院 重庆 400065)
②(中共贵州省委网络安全和信息化委员会办公室 贵阳 550000)
1 引言
近年来,混沌技术作为一种热门的技术被广泛地应用在数字通信之中[1–3],其中最为典型的便是混沌数字调制。与传统的数字调制不同的是,混沌数字调制采用的是混沌信号而非正弦信号,由于混沌信号所具有的不可预测、对初值敏感以及电路简单的特性,采用混沌信号的混沌数字调制在众多调制方式中脱颖而出,成为学界众多学者多年研究的方向。
目前,混沌数字调制技术最主要的两种调制方式分别为差分混沌移位键控(D ifferen tial Chaos Shift Keying,DCSK)[4]以及相关延迟移位键控(Correlated Delay Shift Keying,CDSK)[5],两者都采用了非相关的解调方式,避免了现下还没有解决的混沌同步问题,也是现有混沌调制技术皆倾向于的调制方式。DCSK将参考信号和信息承载信号分开传输,避免了信号间干扰;CDSK改善了DCSK系统的传输速率较低的缺点,同时提高该系统的保密性。与DCSK不同,CDSK将信息承载信号与上一帧的参考信号叠加同时发送,但也因为如此引入了用户间干扰,从而导致了系统的抗噪性能变差。
为了改善通信中存在的高误码率、低传输速率以及保密性差等问题,学术界提出了多种方案[6–11],为了解决用户间干扰问题,文献[12]提出了无信号内干扰的降噪多用户CDSK混沌通信系统,通过对参考信号进行复制,最后经过滑动平均实现降噪,利用W alsh码的正交性,进一步提升传输速率。近些年,许多学者又提出了采用置乱矩阵的调制方案[6,13],文献[14]提出了基于时间反转的多用户差分混沌键控系统,该系统在每个时隙中将参考信号进行反转后传输双倍的信息比特。文献[15]提出多用户分段移位差分混沌键控通信方案,该方案根据传输的用户数的不同,将参考信号分段后进行交换,形成相互正交的信息承载信号。
为了提升传输速率并降低误码率,本文提出一种基于时隙变换的多用户多载波相关延迟移位键控(M u lti-User M ulti-Carrier Correlated Delay Shift Keying system based on T ime Slot T ransform ation,TST-MUMC-CDSK)系统。本系统采用移位后的单位矩阵作为置换矩阵对混沌参考信号进行移位,产生多路正交的混沌信号以承载多用户比特信息,并利用多载波进行传输,提高传输速率的同时降低了误码率。接收端对接收到的信号进行滑动平均,通过对信号分段求和求平均,降低噪声部分的方差,以达到提高系统抗噪声干扰的目的。根据中心极限定理,在扩频因子足够大时,接收端判决变量整体近似服从高斯分布,所以利用高斯近似法(Gaussian Approximation,GA)推导系统在高斯信道和瑞利衰落信道下的理论误码率表达式,并对系统进行蒙特卡罗仿真证明理论推导与仿真结果的一致性。仿真结果表明对比于其他同类多用户系统,所提系统具有更好的抗噪声性能和高传输速率。本系统具有良好的理论价值,且为实际工程应用提供了良好的参考。
本文结构安排如下:第2节分别描述了TSTMUMC-CDSK系统发送端和接收端的模型;第3节为TST-MUMC-CDSK系统的性能分析,分析并推导了本系统分别在多径瑞利衰落信道和高斯信道下的理论误码率公式,并对系统传输效率和能量效率进行对比分析;第4节为系统的仿真结果与分析,对系统进行蒙特卡罗仿真证明理论推导与仿真结果的一致性;第5节结论与展望。
2 系统模型
2.1 TST-MUMC-CDSK发送端
TST-MUMC-CDSK发送框图如图1所示。混沌信号发生器采用2阶Logistic映射产生一段混沌参考序列,长度为β/P,如式(1)所示
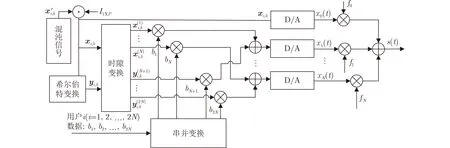
图1 TST-MUMC-CDSK系统发送端框图
其中,h T(t-iT c)是脉冲成形滤波器产生的冲激响应,Tc为码片时间,且一般取1。
混沌信号x i,k通过希尔伯特变换产生正交信号y i,k,并同时通过时隙变换器,分别产生N路序列顺序不同的混沌信号用于承载用户信息:因为混沌随机信号具有良好的互相关特性,所以变化前后的混沌随机信号在不同序列段之间的相关度近似为0,即产生的各路信号之间相互正交,且变化后的序列具有和变化前序列相同的混沌特性,即均值为0,方差为1。时隙变换器首先将输入的混沌信号等分成β/P段,每段长度为P,再经过矩阵组E=[E1,E2,...,Eβ/P]对输入信号进行移位。其中E1是β/P阶的单位矩阵,E2为E1中的所有列向量全部左移1位得到的新矩阵,E3为E2中的所有列向量全部左移1位得到的新矩阵,以此类推,如式(3)所示,产生的信号结构如图2所示
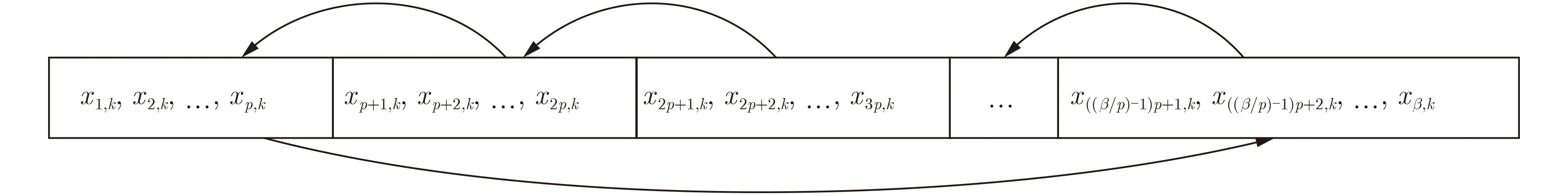
图2 时隙变换结构图
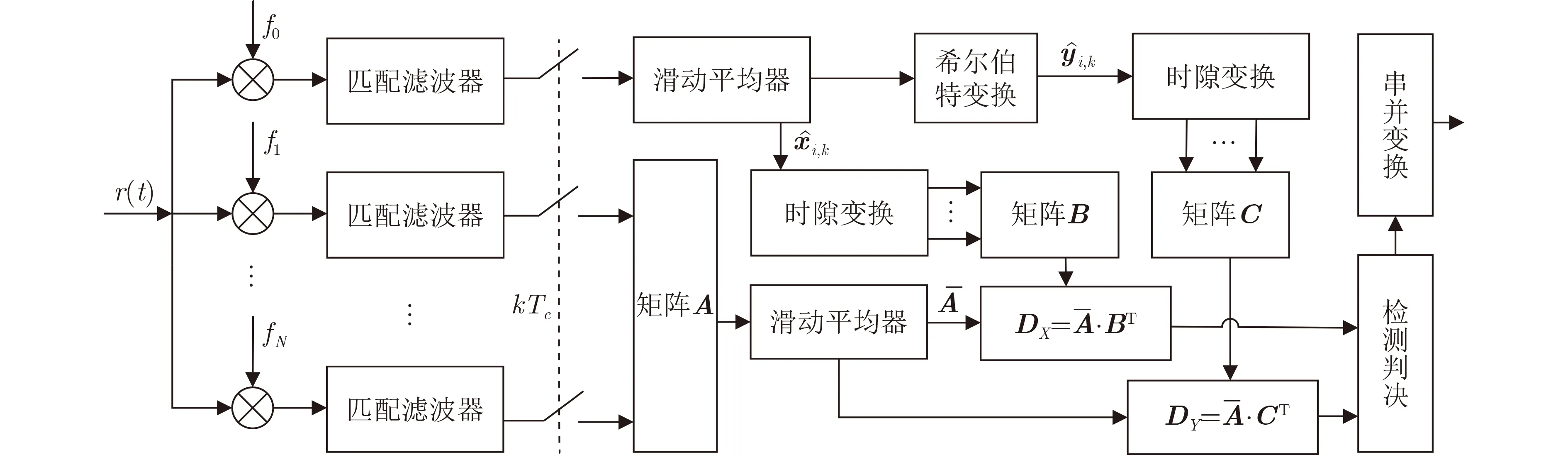
图3 TST-MUMC-CDSK系统接收端框图
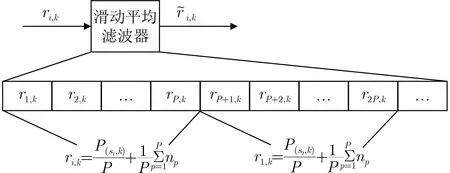
图4 滑动平均滤波器结构
通过时隙变换后得到的信号可以表达为
变换前后的所有信号之间相互正交,即相关值为0,如式(5)表示

则本系统第k帧的发送端信号sk(t)的表达式为

2.2 TST-MUMC-CDSK接收端
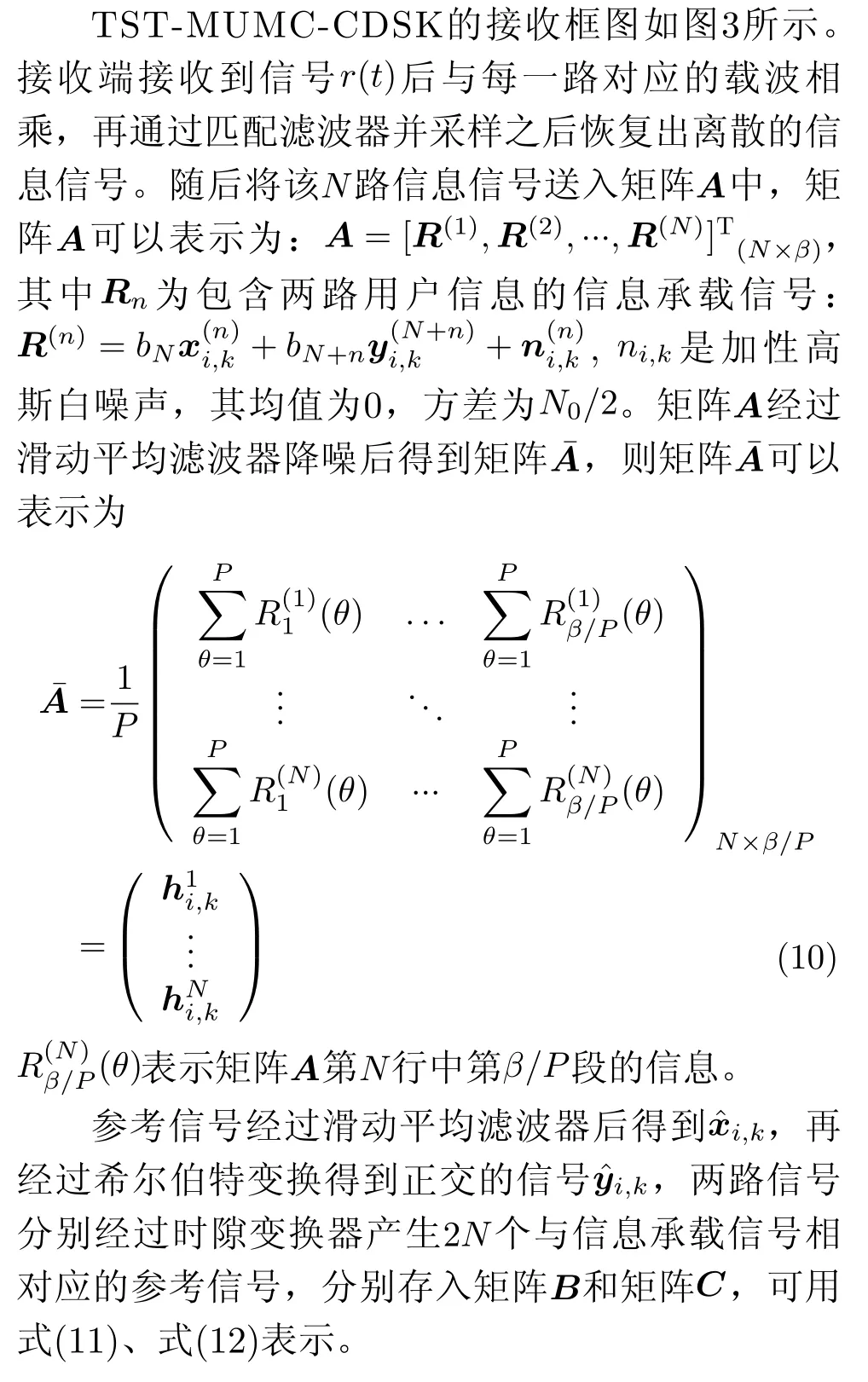


3 性能分析
3.1 BER分析
本文采用2阶Logistic映射产生的混沌参考信号经过归一化后具有以下数字特征:
E(x i,k)=0 ,var(x i,k)=1 ,var(x2i,k)=0,其中,E(·)表示均值,v ar(·)表示方差。
本节将分析该系统在高斯信道和多径瑞利衰落信道下的的抗噪声性能,图5为多径瑞利衰落信道模型。经过该多径瑞利衰落信道后接收到的信号可以表示为r(t)
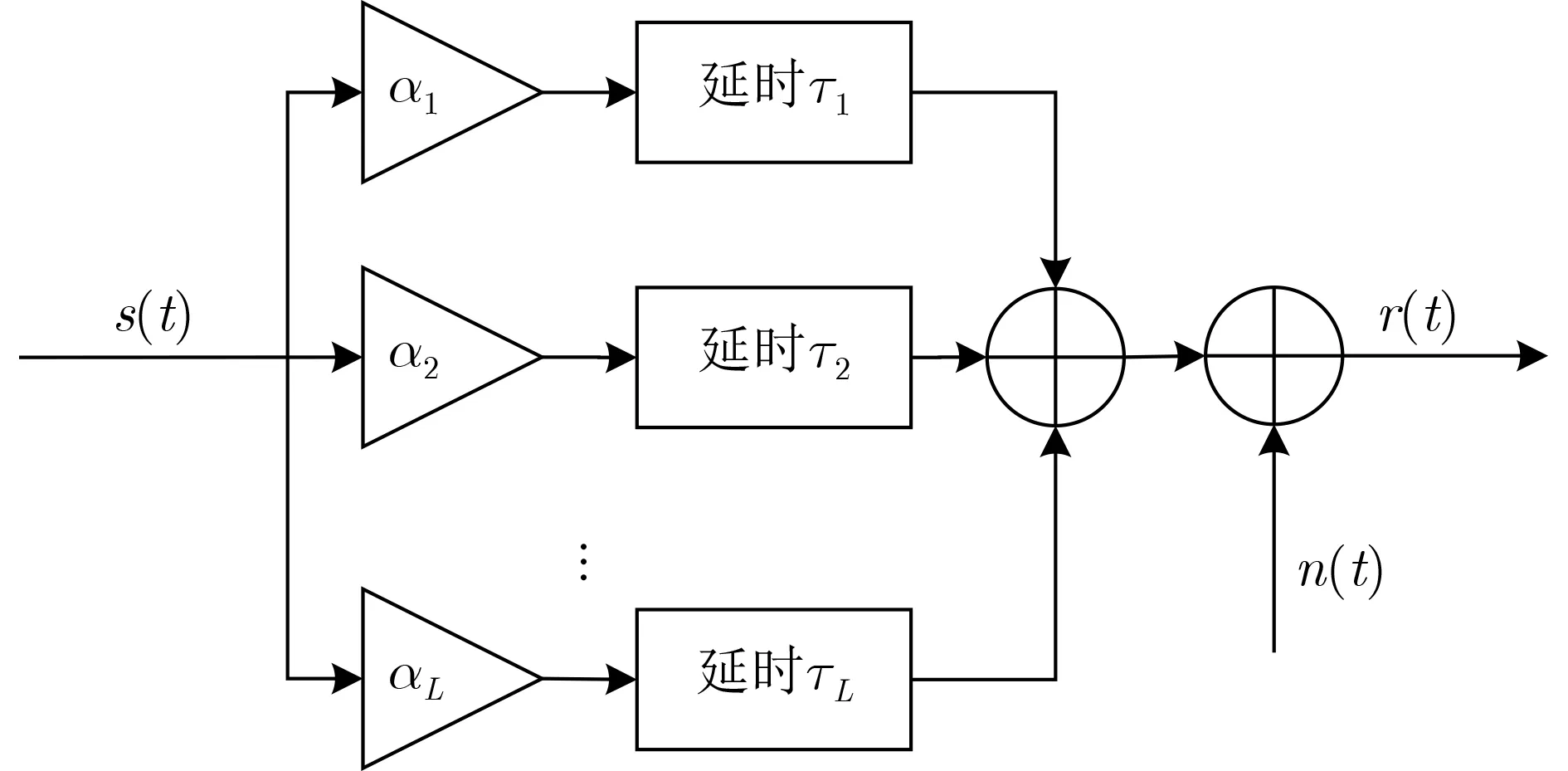
图5 多径瑞利衰落信道模型
其中,L为多径瑞利衰落信道的路径数,αl(l=1,2,...,L)为第l条路径的衰落系数,τl为第l条路径的延迟。假设信道延迟远小于扩频因子,即τl≪β,则符号间干扰便可近似为0,即:≈0,j=(1,2,...,L|j=l)。
采用高斯近似法分析系统误码性能。因为2N个用户信息相互独立,所以只需推导其中1个用户比特的错误概率即可,则第k帧的第n个用户比特信息的相关器输出为
E为有用信号,F为信息承载信号与噪声的干扰项,G是噪声之间的干扰项。理论误码率公式为


3.2 TST-MUM-CDSK系统传输效率、能量效率分析
本节将分析TST-MUMC-CDSK系统的比特传输速率、平均比特能量以及能量效率,并将之与其他同类系统进行比较。以与传统的CDSK系统对比为例

从表1可以看出,本文所提系统在传输速率上优于N ISI_MU_CDSK系统,与NR_M UCDSK相同,并且在能量效率上均优于这两个多用户系统。
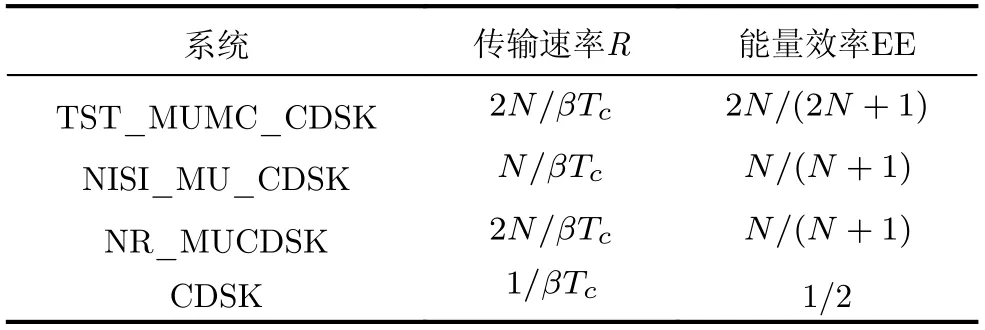
表1 TST_MUMC_CDSK与其他系统的传输速率和能量效率对比
如图6表示本文系统相对于其他系统所提升的传输速率百分比Rd和节约的平均每比特能量百分比EB随 用户数N增加的变化曲线,图7将TST-MUMCCDSK系统与其他系统的能量效率作对比。从中可以看出,本系统因为传输多路信息比特而只传输1路参考信号,降低了平均每比特能量。
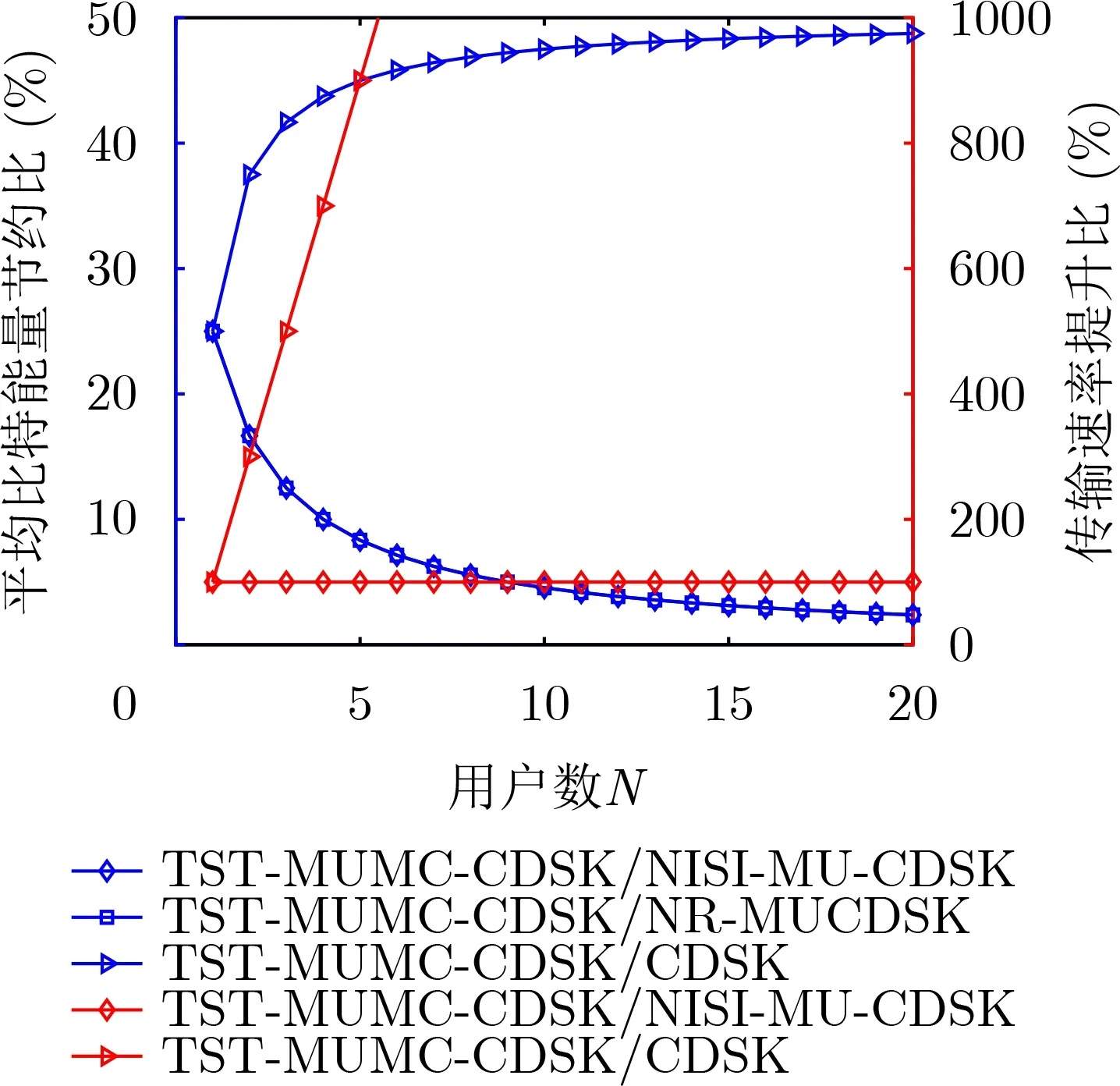
图6 R d和E B与其他系统对比
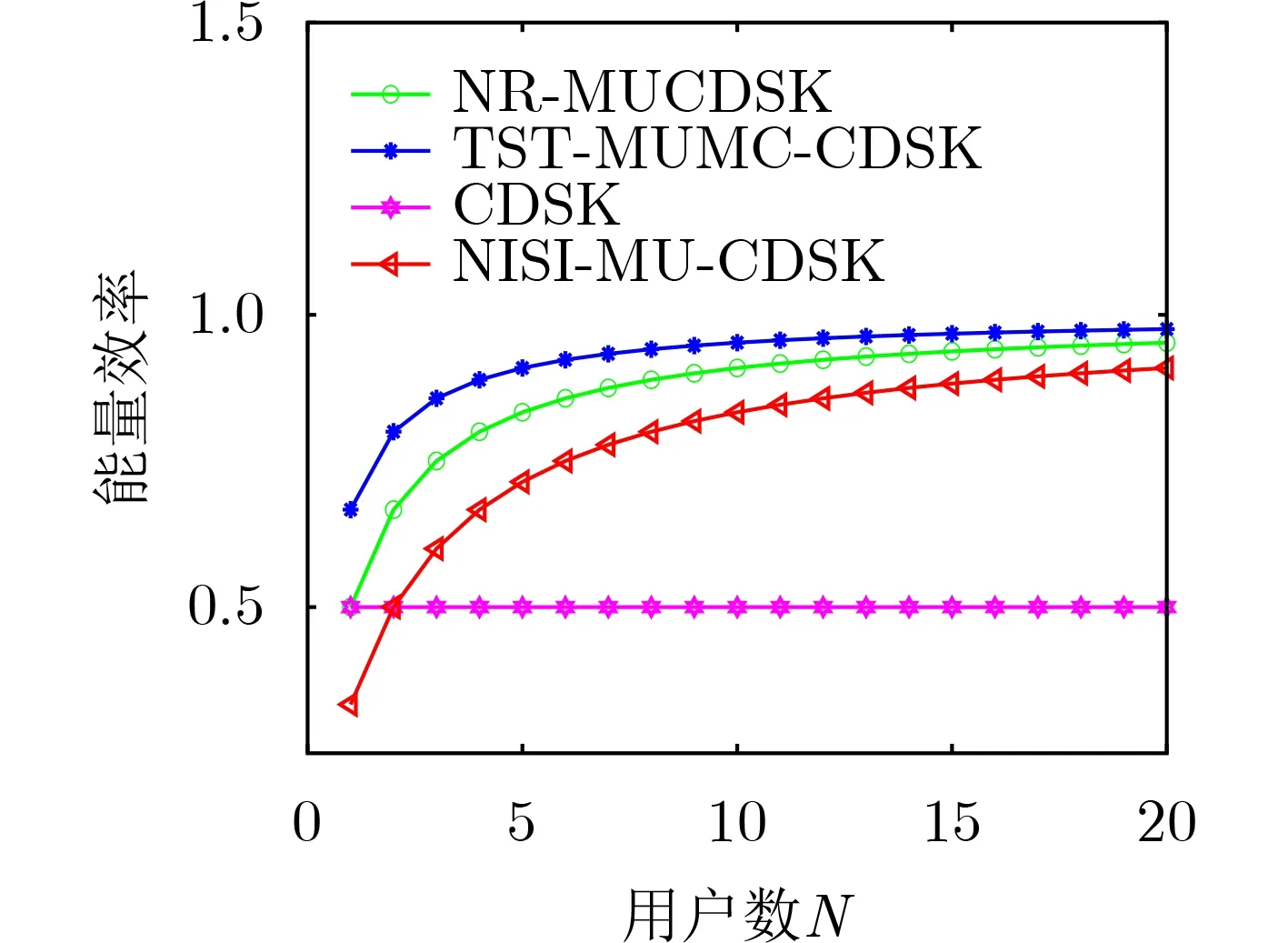
图7 与其他系统的能量效率对比
4 系统仿真结果和分析
本节对TST_MUMC_CDSK系统分别在高斯信道和多径瑞利衰落信道下的误码率进行了蒙特卡罗仿真,并与理论公式进行对比,仿真结果均是在仿真进行106次所得。
图8给出了TST_MUMC_CDSK系统与其他多用户系统的误码率对比。参数分别为:β=256,P=8,N=8,仿真在高斯信道下进行。从中可以看出,本文所提系统要明显优于其他系统,拥有更低的误码率和更好的抗噪声性能。
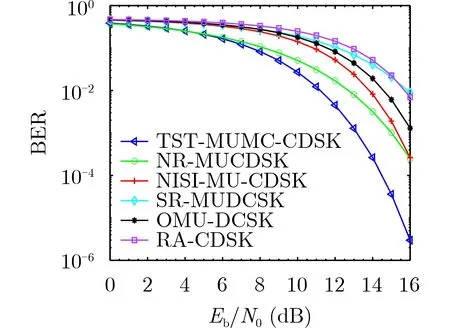
图8 TST_MUMC_CDSK系统与其他系统的对比
图9给出了高斯信道下TST_MUMC_CDSK系统误码率在不同Eb/N0时随着扩频因子β变化的曲线。Eb/N0分别取8 dB,10 dB,12 dB和14 dB,其他参数分别为N=4,P=8。在扩频因子β较小时,仿真结果和理论推导数值吻合度较差。这是因为高斯近似法所具有的局限性:当β较小时,其判决变量不满足高斯分布,导致仿真值与理论值有较大偏差。
如图10(a)给出了系统误码率在高斯信道和多径瑞利衰落信道下不同扩频因子β时随着Eb/N0变化的曲线。扩频因子分别取β=128,256,512。其他参数为:N=4,P=8。多径瑞利衰落信道为3径等增益信道,即E(α12)=E(α22)=E(α32)=1/3。从中可以看出,当扩频因子β=128时,系统的抗噪声性能最好,并且随着扩频因子的增加,抗噪声性能逐渐下降。这是因为随着β的增加,噪声产生的干扰部分的方差变大,导致误码率变高。
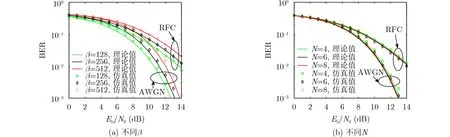
图10 BER在高斯信道和多径瑞利衰落信道下随E b/N 0的变化
如图10(b)给出了系统误码率在高斯信道和多径瑞利衰落信道下不同用户数N时随着Eb/N0变化的曲线。用户数分别取值为:N=4,6,8,其他参数分别为:β=256,P=8。多径瑞利衰落信道为3径等增益信道。从中可以看出,当用户数N增加时,BER逐渐降低。这是由于当用户数增加时,系统的平均比特能量Eb降低,从而导致系统的误码率降低。
如图11给出了系统误码率在瑞利衰落信道下不同路径数L时随着Eb/N0变化的曲线。路径数分别取:L=2,3,4,5,信道为等增益信道。其他参数分别为:β=256,P=8,N=6。从中可以看出,在多径瑞利衰落信道下,随着路径数的增加,系统具有更好的抗噪声性能和更低的误码率。图12给出了系统误码率在多径瑞利衰落信道下等增益和不等增益,β分别取β=256和β=512时随Eb/N0变化的曲线。等增益时为3径等增益信道,即E(α12)=E(α22)=E(α32)=1/3,3径不等增益信道的各路径平均增益分别为:E(α12)=1/111,E(α22)=10/111,E(α32)=100/111。从中可以看出,等增益时系统的误码率明显低于不等增益时。
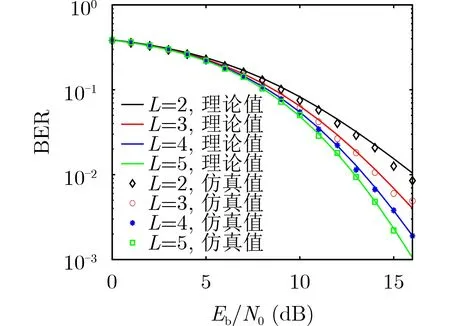
图11 L不同,BER随E b/N 0的变化
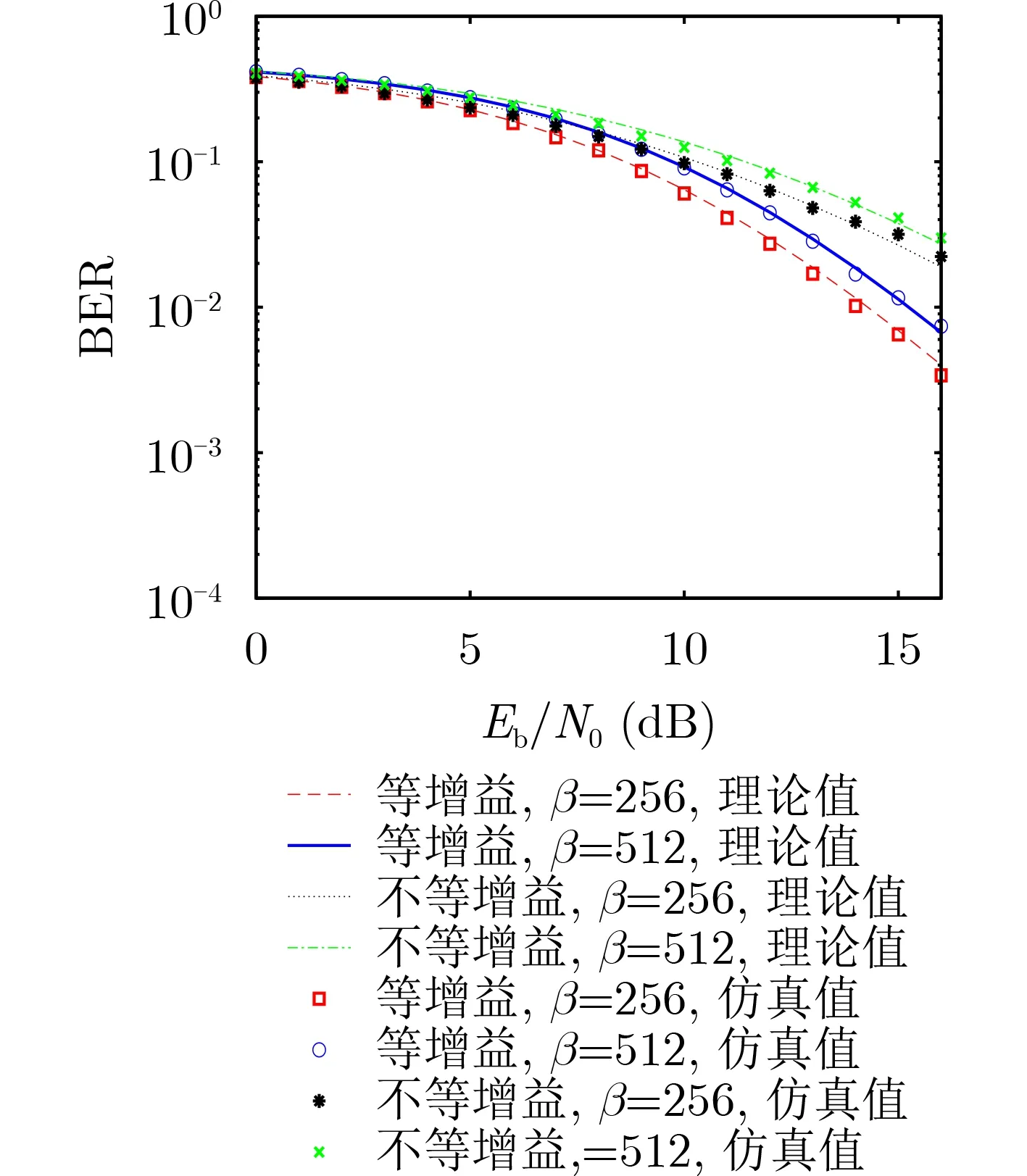
图12 等增益与不等增益,BER随E b/N 0的变化
如图13给出了该系统在AW GN信道下的BER随扩频因子β和Eb/N0变化的3维图。其他的参数分别取:N=4,P=4。从中可以看出,当Eb/N0不变时,系统误码率随着扩频因子的增加而增加,并且当信噪比Eb/N0较小时,扩频因子变化对系统BER带来的影响也逐渐变小,此时Eb/N0对系统的BER影响占主导地位。
图14给出了本系统在AWGN信道下的BER随复制次数P和Eb/N0变化的3维图。其他的参数分别取:β=256,N=4。从中可以看出,较大的复制次数可以给系统带来更好的抗噪声性能,且复制次数一定时,系统误码率随着Eb/N0的增加而减少。
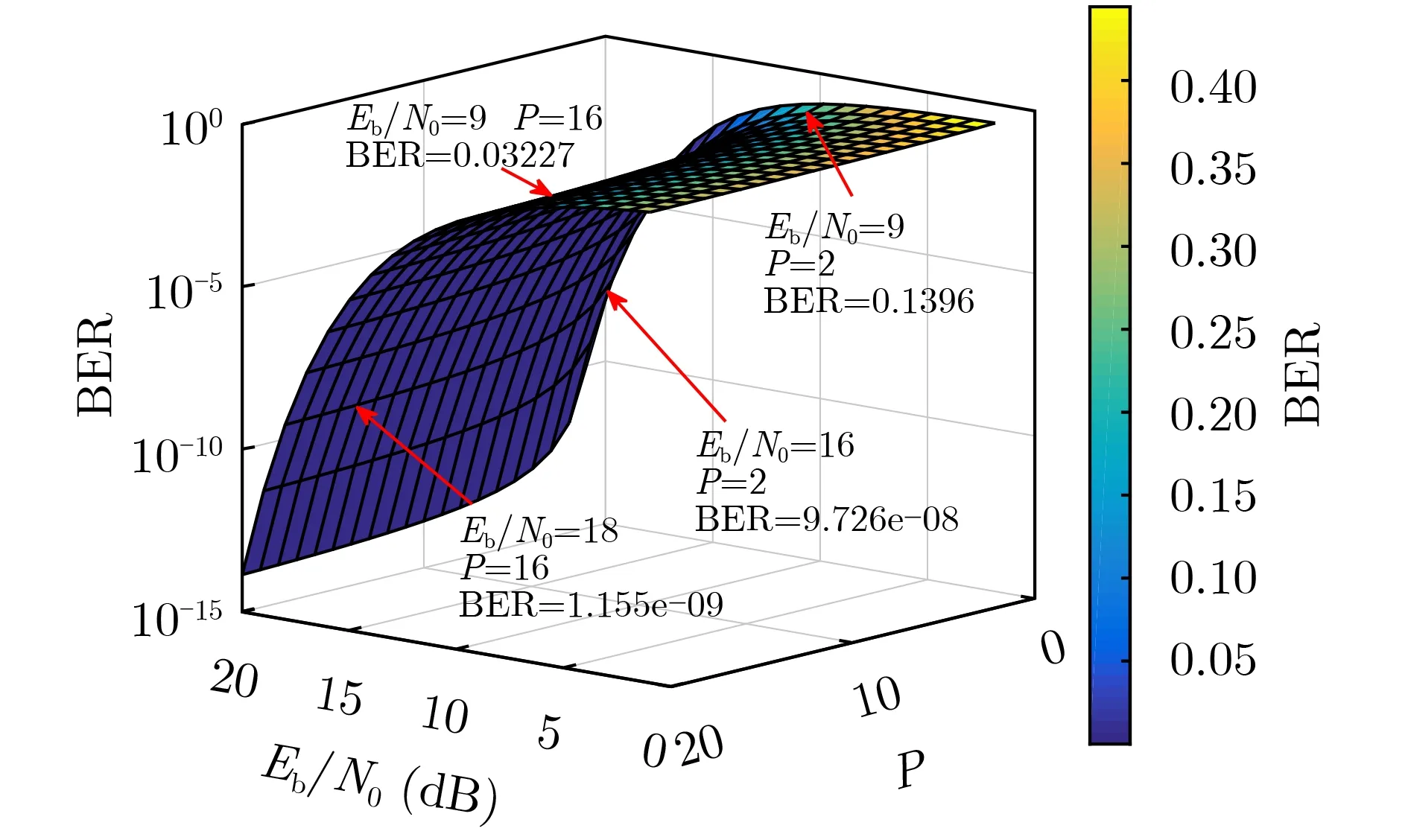
图14 BER随P 和E b/N 0变化3维图
5 结束语
本文所提TST-MUMC-CDSK系统通过时隙变换器将复制P次之后长度为β的混沌序列等分成β/P段后进行移位操作,产生N个相互正交的混沌序列。再经由希尔伯特变换,共产生 2N个相互正交的混沌序列同时传输 2N个用户信息。在接收端对接收到的信号进行滑动平均,以达到降噪的目的。最后用GA法推导本系统在高斯信道和多径瑞利衰落信道下的理论误码率公式,通过理论分析以及数值仿真验证了理论推导的正确性。通过与其他系统的对比,本文所提系统误码率均明显低于其他系统,即在满足同样误码率的同时该系统只需更低的Eb/N0。如:在误码率同为10–2时,本系统所需的Eb/N0比NR_M UCDSK系统低1.5 d B,比NISI_MU_CDSK系统低2.6 dB;在误码率同为10–3时,本系统所需的Eb/N0比NR_MUCDSK系统低1.9 dB,比NISI_MU_CDSK系统低2.2 dB;进一步表明该系统误码性能方面的优越性。
本文下一步工作是在该系统的基础上进一步提高系统的能量效率,降低平均比特能量,探索该系统应用于实际工程中的可行性。
