可重构智能表面辅助的毫米波信道估计算法

郭 甜 张旭辉 吴雨佳 王 悦

①(西安科技大学机械工程学院 西安 710054)

②(陕西省矿山机电装备智能检测重点实验室 西安 710054)

1 引言

大规模M IMO和毫米波通信技术作为5G移动通信系统的关键技术，由于其在基站端配置大量天线，导致系统较高的功率消耗；毫米波由于其传输损耗高，并且易受障碍物的阻挡，使得通信的覆盖范围低[1]。为了降低通信系统的功率消耗，增加通信的覆盖范围，可重构智能表面(Recon figurab le Intelligent Surface,RIS)具有低功耗、低成本且易于部署等优点，可通过调节其反射元件的相位达到对无线环境进行智能调控，从而改变无线通信环境，已成为6G移动通信系统的潜在关键技术之一[2]。RIS的研究方面主要有：RIS辅助无人机通信[3]，RIS辅助通信系统能效[4]，全息多输入多输出表面(Holographic M IMO Surface,HM IMOS)在通信系统中的应用[5]，RIS辅助物理层安全[6]，RIS辅助通信感知一体化[7]等。

基于RIS辅助的毫米波通信系统研究已受到学术界和产业界的广泛关注，其带来通信系统的覆盖率增强，抗衰落和抗干扰等性能提高，然而这些性能提高取决于精确的信道状态信息的获取。但是由于RIS的无源反射特性，难以对信号进行处理。因此，对基于RIS辅助的通信系统的信道估计产生了很大的挑战。

目前，RIS辅助的通信系统的信道估计主要有以下两个方面：一方面为级联信道估计，即联合估计基站(Base Station,BS)到RIS的信道，RIS到用户(User Equipment,UE)之间的信道；另一方面为分离信道估计，即分开估计BS-RIS,RIS-UE信道。在级联信道估计中，文献[8]采用并行因子求解信道，由于该算法未考虑毫米波信道的角域稀疏性，系统的信道估计开销增加。毫米波信道通常被认为是稀疏的，可用压缩感知理论来求解信道估计。文献[9]利用级联信道的稀疏结构将RIS辅助的信道估计问题转化为压缩感知问题，并采用正交匹配追踪算法进行求解。压缩感知类算法是利用信号的角域稀疏性来进行信道角度信息估计，对连续分布的角度进行离散化会产生误差，从而导致信道估计的精度降低。由于RIS在实际的部署中，BS-RIS的相对安装位置往往固定不变，可假设BS-RIS之间的信道是固定不变的。而用户随时可以移动，即RIS-UE之间的信道是时变的。因此，对BS-RIS和RIS-UE的信道进行分离信道估计更符合实际需求。在分离信道估计方中，文献[10]采用双时间尺度进行分离信道估计，降低了总体导频开销。为了提高信道估计精度，文献[11]采用基于原子范数最小化(A tom ic Norm M inim ization,ANM)方法作用于信道角度参数的估计。基于原子范数最小化方法由于对信道角度进行连续的稀疏恢复，因此估计精度有所提升。但该文献考虑的是RIS采用均匀线性阵列(Uniform Linear A rray,ULA)结构，不符合实际情况。

为了提高RIS辅助下信道估计的性能，一些研究通过为RIS的少量元素安装射频(Radio Frequency,RF)链来辅助信道估计[12–14]。文献[12]采用2维多信号分类算法(Two Dimensional MU lti-SIgnal Classification algorithm,2D-MUSIC)对信道的离开角和到达角度同时进行估计。文献[13]采用求根多重信号分类算法(ROOT MU lti-SIgnal Classification algorithm,ROOT-MUSIC)估计信道的角度参数。以上文献的方法是基于MUSIC算法，其在信噪比较高的情况下估计性能较好。文献[14]采用2维快速傅里叶算法对信道的角度进行估计，并通过信号补零以获得更加精确的信道估计值。采用2维快速傅里叶算法(Two Dimensional Fast Fourier Transform,2D-FFT)求解信道的角度参数，算法的复杂度较低，但是该算法信道估计的精度与信号补零的个数有关，补零个数的增加虽然可以提高信道估计的精度，但是也会提高算法的复杂度。

为提高RIS辅助的毫米波系统的信道估计的性能，并降低算法的复杂度，考虑给RIS部分无源器件安装RF链，以分离估计BS-RIS,RIS-UE信道。采用基于原子范数最小化的稀疏重构算法，利用信号协方差矩阵的Toep litz结构特性，有效提高了信道的估计精度。为了降低问题求解的复杂度，采用交替方向乘子法(A lternating Direction M ethod of Multipliers,ADMM)对信道的参数进行求解，通过联合优化信道参数和迭代步长以获得更加精确的信道估计值，并通过所获得的角度参数和信道矩阵参数获得路径增益，从而最终得到信道估计值。仿真结果表明，本文算法在保持较低计算复杂度的同时，提高了系统信道估计性能。

2 系统模型

考虑RIS辅助的毫米波上行通信系统的信道估计，系统模型如图1所示。BS和UE分别配备N根和K根天线[8]，RIS由NRIS个反射元件组成，NRIS=N1×N2,N1,N2表示RIS的水平和垂直侧反射元件数目。

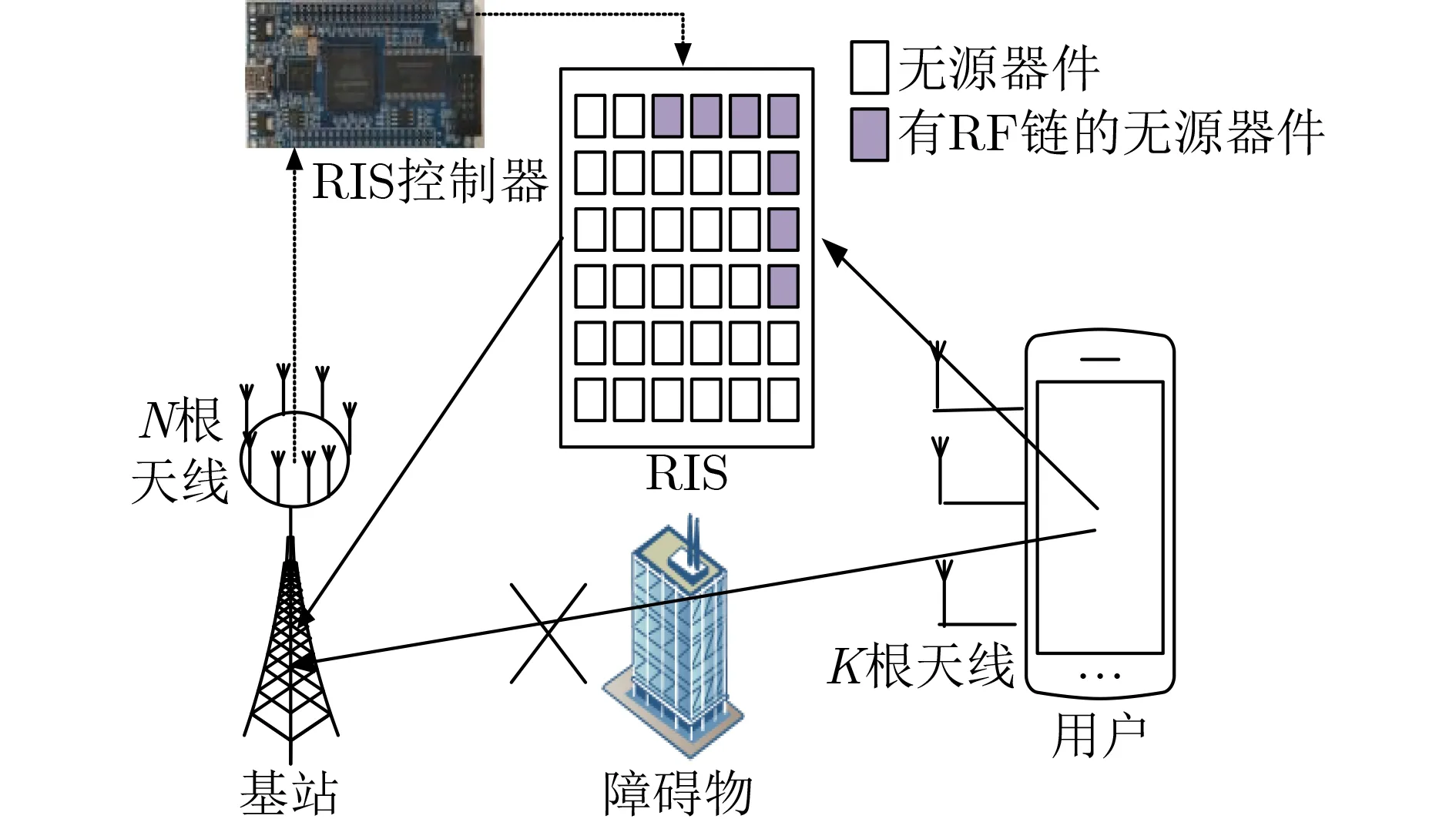
图1 RIS辅助的毫米波上行通信系统模型

由于RIS只反射信号，难以对信号进行处理，因此，考虑在RIS的部分无源器件上安装L型的RF链路。假设UE-BS的直接链路被障碍物所阻挡，UE-BS的通信采用RIS提供的反射路径来辅助通信。系统采用时分双工模式，根据用户发送导频符号进行上行信道估计，下行信道的CSI通过信道的互易性获得。假设RIS辅助的毫米波通信信道的训练阶段由T个连续的时间帧组成，每个时间帧包含Q个时隙[13]。因此，在第t个时间帧中，导频符号经RIS反射到BS的接收信号Yt表示为

3 信道模型

由于毫米波信道的稀疏性，本文采用S-V信道模型。考虑BS和UE端配备ULA,RIS端配备均匀平面阵列(Uniform Plane A rray,UPA)。由于RIS上安装L型RF链，将信道的估计问题分为两部分：第1部分为UE到R IS的信道估计，第2部分为R IS到BS的信道估计。UE-RIS和RIS-BS的信道分别表示为

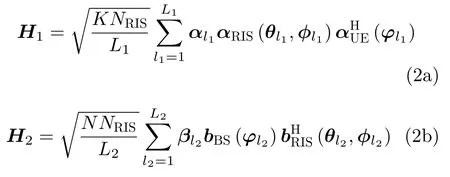
其中，L1,L2分别表示UE-RIS,RIS-BS的路径个数，αl1,βl2分别表示UE-RIS的第l1条路径的复增益，RIS-BS的第l2条路径的复增益。(θl1,ϕl1)表示RIS处的第l1条路径的到达角(Angle O f A rrival,

4 信道估计

本文采用分离信道估计方法，根据式(2)可知，只需要估计信道的角度参数以及路径增益，即可恢复信道矩阵。由于安装RF链，RIS有两种工作模式，反射模式和接收模式。在估计UE-RIS信道时，RIS工作在接收模式，可利用RF链对RIS接收的信号进行处理，从而在RIS端进行估计该信道；在估计RIS-BS的信道时，RIS工作在反射模式下，BS接收RIS反射的信号，从而在BS端对该信道进行估计[14]。

4.1 H 1信道矩阵参数估计

首先对UE-RIS的信道H1中的角度参数以及路径增益进行估计，即角度参数需要估计UE的AOD和RIS的AOA。由于RIS采用UPA结构，估计AOA需要估计RIS的方位角和仰角两种角度信息。传统的基于原子范数最小化的方法不能直接对3维角度进行估计。因此，利用RIS上安装的L型RF链的水平方向阵列估计RIS的方位角和垂直方向阵列估计RIS的仰角，在各个方向上只需要估计两种角度信息。因此，本文的信道矩阵参数估计方法步骤如下：

首先证明RIS上RF链接收信号的协方差矩阵满足双重Toep litz结构，采用基于解耦原子范数最小化算法进行求解；其次，为了降低该 半正定规划(Sem i-Definite Programm ing,SDP)问题求解的复杂度，采用改进的快速ADMM算法进行求解，该改进算法采用动量梯度下降法进行信道参数变量更新，并通过联合优化迭代步长和信道矩阵参数，提高信道估计的精度，通过该改进算法即得到UE处的AOD和RIS的方位角的2维角度信息和信道矩阵参数；最后，通过所获得的角度参数和信道矩阵参数估计路径增益。根据以上步骤，可获得UE处的AOD和RIS处的AOA，即可恢复信道矩阵。H1信道矩阵参数的估计过程如图2所示。

图2 H 1信道矩阵参数的估计过程

4.1.1H1信道矩阵角度参数估计

RIS端部分无源器件上配置“L”型RF链路，该RF链在水平和竖直方向上的导向矢量分别表示为

其中，⊗,(◦), (*), v ec(·)分别表示矩阵的K ronecher积、Khatri-Rao积、共轭、向量化。I n x表示单位矩阵，采用T个时间帧进行训练时，式(6)可以写为

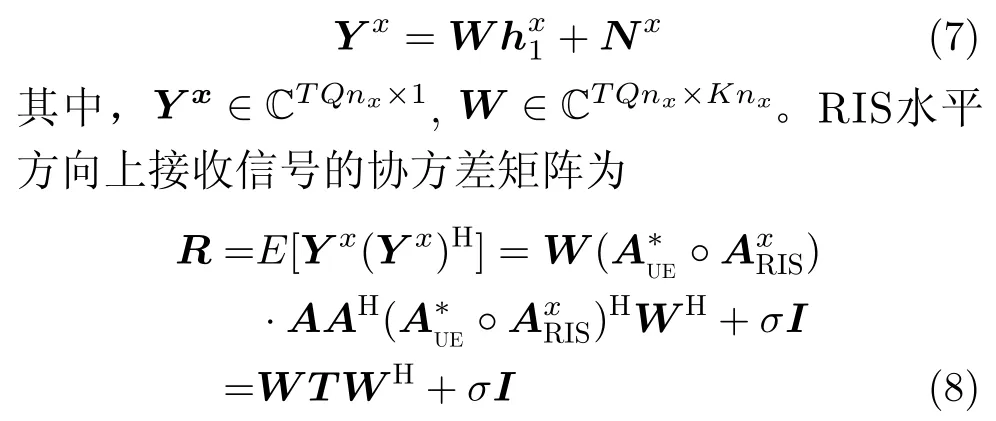
其中，T∈CK n x×K n x为半正定具有双重Toep litz结构的矩阵。由于T表达式中含有UE-RIS水平链路信道矩阵的离开角和到达角参数。因此通过求解T，可得到信道矩阵的角度参数。由于T满足双重Toep litz结构，因此，将求解UE-RIS水平链路的信道估计问题转化为基于解耦原子范数最小化的SDP问题

式(9)可通过 MATLAB中凸优化工具箱(ConVeX,CVX)进行求解，由于通过CVX求解的算法复杂度为求解的半正定矩阵维度的3.5次方[16]，因此，本文采用改进ADMM算法以降低算法的复杂度。ADMM算法的核心在于：通过对问题进行分布式优化，即对一个多变量优化问题进行解耦，通过对每个单变量进行迭代求解来简化问题本身的计算量[17]。因此，通过引入一个新的变量U，将原始的优化变量的约束去掉，即将式(9)改写为

其中，F为式(10)的目标函数。〈a,b〉表示矩阵a与b的内积，即〈a,b〉=tr(bHa)，Λ为拉格朗日乘子，p为惩罚项，p=1。通过式(11)，将式(10)转化为无约束优化问题(先忽略U≽0约束，在接下来求解U时考虑这一约束)。因此，根据ADMM算法，优化变量的更新步骤为

其中，β ∈(0,1),ξ∈(0,0.5)，dt为式(11)函数的下降方向。采用动量梯度下降法对信道矩阵参数进行更新，其更新公式为

其中，δ为动量项，且初始化为0，γ为关于动量项的超参数，γ=0.9。因此，本文联合优化迭代步长和信道参数的计算步骤如算法1所示。

其中，T*是T的伴随矩阵，e1=[1,0,...,0]T。接下来计算U的更新表达式，由于式(11)中只有最后一项与U有关，并考虑U≽0约束，即寻找使

其中，Σ+表示将Σ中所有负的特征值置为0后，得到的新的特征值矩阵。因此，根据式(15)—式(17)迭代更新的值。

与采用CVX求解器求解的算法复杂度相对比，本节采用改进的ADMM算法，本算法利用动量梯度下降法对信道参数进行更新，避免矩阵的求逆过程，并通过对迭代步长和信道矩阵参数的联合优化，提高信道估计的精度。因此，本文所提算法在保持信道估计的精确性的同时，算法复杂度降低，运行速度更快。

由于式(18)中范德蒙德分解的形式与MUSIC算法中接收信号协方差矩阵的形式一样。因此，采用Root-MUSIC算法，转化为多项式的求根问题，即可得到和的角度信息，进而根据m atrix pencil算法进行角度的自动配对[18]。根据上述的基于解耦原子范数最小化算法和改进的ADMM算法可以得到和的角度信息，同理可以用相同的方法，得到RIS上的仰角ϕ˜的估计值。

4.1.2H1路径增益估计

4.1.3信道矩阵重建

根据4.1.1节的解耦原子范数最小化算法和改进的ADMM算法可获得UE处的AOD和R IS处的AOA；根据4.1.2节方法可获得H1的路径增益。因此，根据式(2)，可获得重建矩阵为

4.2 H 2信道估计

因此，本文所提基于RIS辅助的毫米波信道估计的D-ANM+改进ADMM算法流程图如算法2所示。

5 算法复杂度分析

本文所提D-ANM+改进ADMM信道估计算法的复杂度主要由信道矩阵H1和H2中的角度参数估计和路径增益估计两部分组成。由于求解信道矩阵H2的算法与信道矩阵H1的算法相同，因此只分析求解H1的算法复杂度。由于采用动量梯度下降法对信道矩阵参数进行更新，在更新时，需要求解的梯度，该过程仅涉及矩阵的乘法运算，其复杂度为O(n x K L1+n x K)，对(u x,u y,Λ)更新时，只涉及每个矩阵的加减运算，计算复杂度可忽略，对U进行更新时，由于需要进行特征值分解，计算复杂度为O(n x(n x+K)2)。因此所提出的算法的复杂度为O(n x K L1+n x K+n x(n x+K)2)；其次，采用ROOTMUSIC算法和matrix pencil算法对角度进行求解和配对，其求解的计算复杂度表示为最后求解信道的路径增益，其计算的复杂度为O((L1n x)3)。由于L1≪{N,K,NRIS},nx≪NRIS。因此，求解H1的算法复杂度为O(n x(n x+K)2)。本文算法和文献[8,12–14]的算法复杂度对比分析如表1所示。

表1 本文算法与相关文献算法的复杂度对比

算法2 D-ANM+改进ADMM信道估计算法

6 仿真分析

本节中通过仿真实验来评估本文所提的D-ANM+改进ADMM信道估计算法与现有文献中的ALS算法[8]、2D-MUSIC算法[12]、ROOT-MUSIC算法[13]、2D-FFT算法[14]系统性能的对比。在仿真中，设置BS端天线的数目N=32，其中RIS的水平/垂直射频链的数目n x=n y，导频符号数Q=20,T=50。UE-RIS和RIS-BS信道的路径L1=L2=4。根据原子范数算法的角度分辨率要求，UE-RIS和RIS-BS信道的不同路径之间的正弦差sin(θ1)-sin(θ2)≥4/N,4/K,4/NRIS。

采用均方根误差(Root M ean Squared Error,RMSE)评价信道矩阵的角度参数的性能指标，表达式为

其中，R表示蒙特卡罗运行的次数，R=500，(θ,φ)表示RIS的方位角和仰角真实的角度值，表示RIS的方位角和仰角估计的角度值。

采用两种系统性能评估指标对本文算法与相关文献算法的信道估计性能进行对比，第1种性能指标为：归一化均方误差(Normalized M ean Square Errror,NMSE)，其表达式为

其中，H表示真实的信道值，表示估计的信道值。

第2种性能指标为频谱效率(Spectra l E fficiency,SE)，由于本文不涉及发送端的基带预编码器和接收端的合并器设计，因此，对信道矩阵H进行奇异值分解，假设预编码器W和合并器F的取值分别为所估计的信道矩阵H的L1个左右奇异向量[11]。考虑R IS的离散相移矩阵Φ，从中选择RIS的相移矩阵Φ的每个元素。因此，根据文献[11]，频谱效率的表达式为

图3给出了克拉美罗下界(Cram er-Rao Lower Boun d,CRLB)[19]、本文所提D-ANM+改进ADMM算法、2D-MUSIC算法和2D-FFT算法估计得到的RIS的角度的均方根误差性能对比。由图可知，本文所提算法的角度估计的均方根误差和CRLB相接近，这是由于本文采用解耦原子范数最小化算法，该算法是利用信号的协方差矩阵的Toep litz特性，对连续的角度进行稀疏化，避免了网格失配问题，因此提高了角度估计的精度。随着信噪比的增加，本文算法角度估计的均方根误差和CRLB逐渐接近。而2D-MUSIC算法是将连续的角度离散化，角度的估计精度与离散化的角度之间的间隔有关，本文采用0.1°的角度间隔来搜索。2D-FFT算法根据信号空间谱进行谱峰搜索以获取信道的角度估计值，由于采用信号补零方法增加信号的频谱点，因此，信道估计的性能和信号补零的个数有关，本文假设对信号补零后的维度为256。因此，本文算法角度估计值达到了良好的性能。

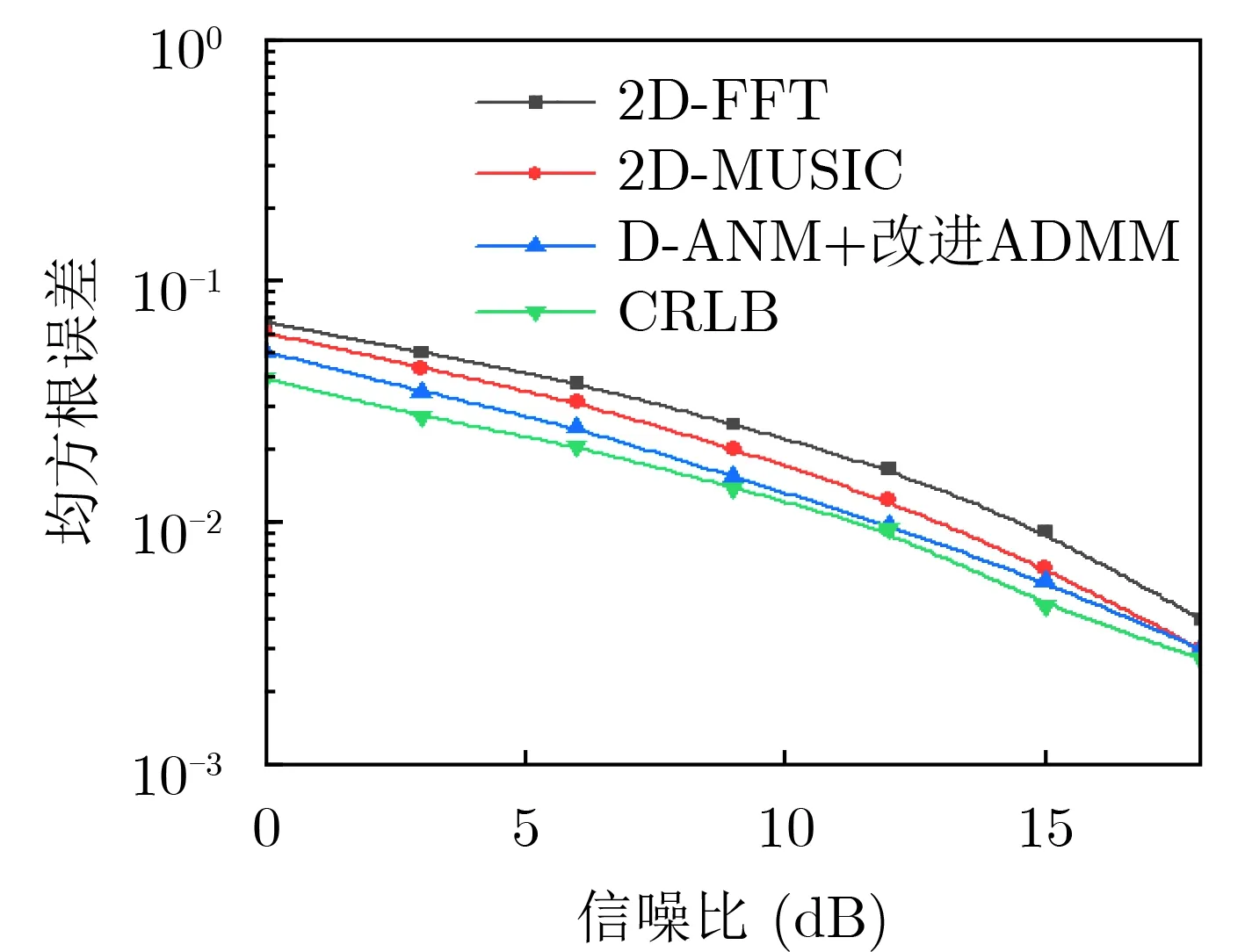
图3 不同算法求解RIS的角度均方根误差性能对比

图4给出了UE-RIS的信道H1,RIS-BS的信道H2估计的归一化均方误差系统的性能对比。由图4可知，随着RIS上配置的射频链个数的增加，信道估计的性能也逐渐增加。这是由于射频链数目的增加，信道估计的准确性增加。随着信噪比的增加，信道H1和信道H2的估计性能逐渐增加，这是由于信噪比的增加，信道环境变好，因此信道估计性能增加。该结果验证了本文所提的信道估计算法在UE-RIS和RIS-BS分离信道估计时均能保持良好的系统性能，由此验证了本文算法的可行性。

图4 信道H 1与 信道 H 2估计性能对比

图5当信噪比为20 dB时，本文提出的改进ADMM算法与文献[11]采用CVX求解器算法的运行时间对比。由图可知，随着用户天线数的增加，改进的ADMM算法的运行时间曲线的斜率远小于采用CVX求解的斜率，即改进ADMM算法的运行速度比CVX求解器快得多。采用CVX求解的SDP问题的算法是采用内点算法求解的，其算法复杂度为log2(1/ε))[16]，ε为目标的精度。采用ADMM求解SDP问题的算法复杂度为O(n x(n x+K)2)，由于ADMM在每次迭代中的参数更新都是以封闭形式进行的，所以运行速度较快。因此，本文所提出的算法运行时间较快，并且比较适合大型阵列。

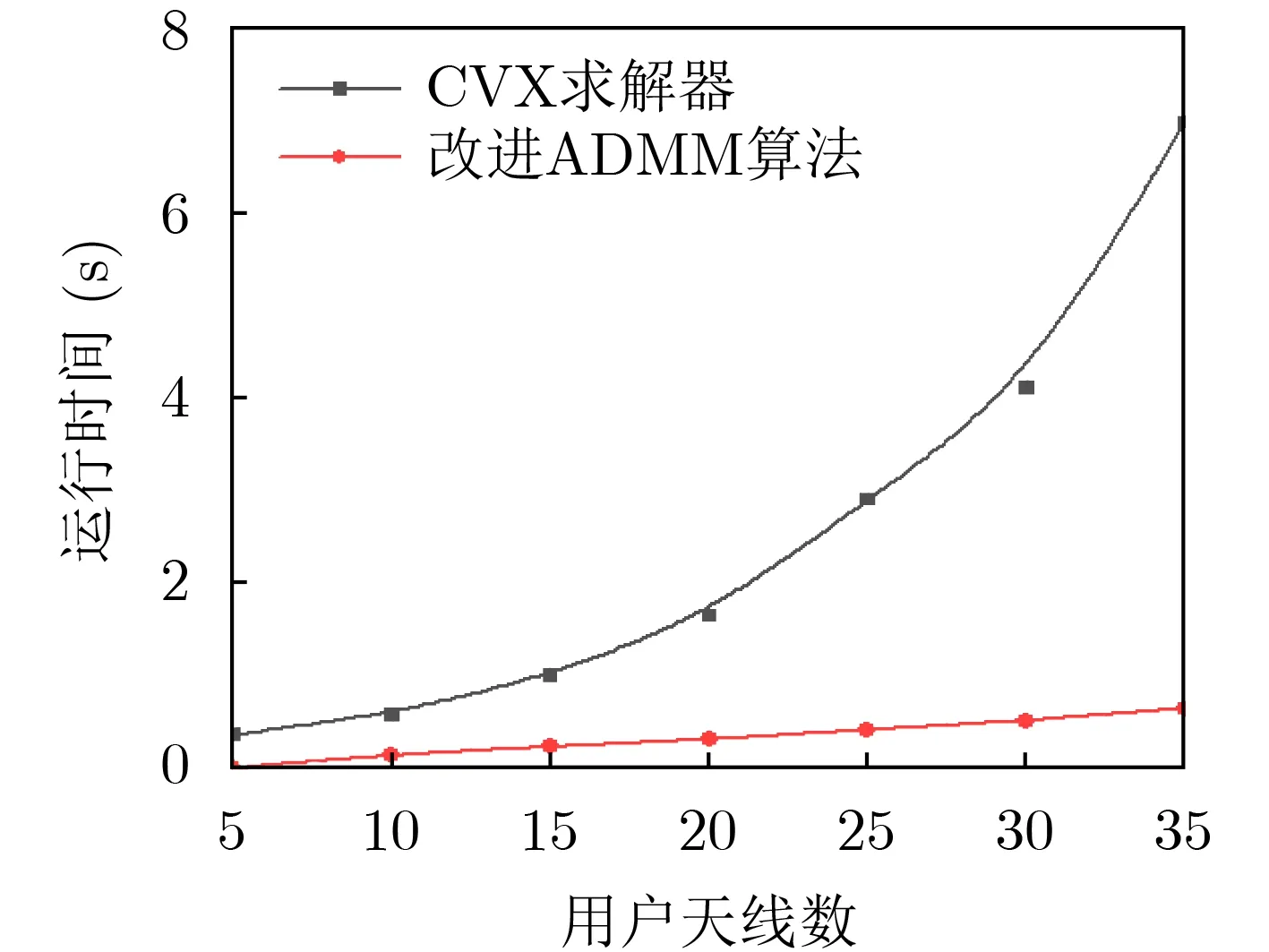
图5 本文算法与CVX算法的运行时间对比

图6给出了当R IS上配置的射频链数目分别为4,10,14时，系统的频谱效率性能的变化情况。由图可知，随着射频链数目的增加，频谱效率也逐渐增加。当射频链数目增加时，能接收到更多的信道信息，因此系统的信道估计性能提高，频谱效率增加。

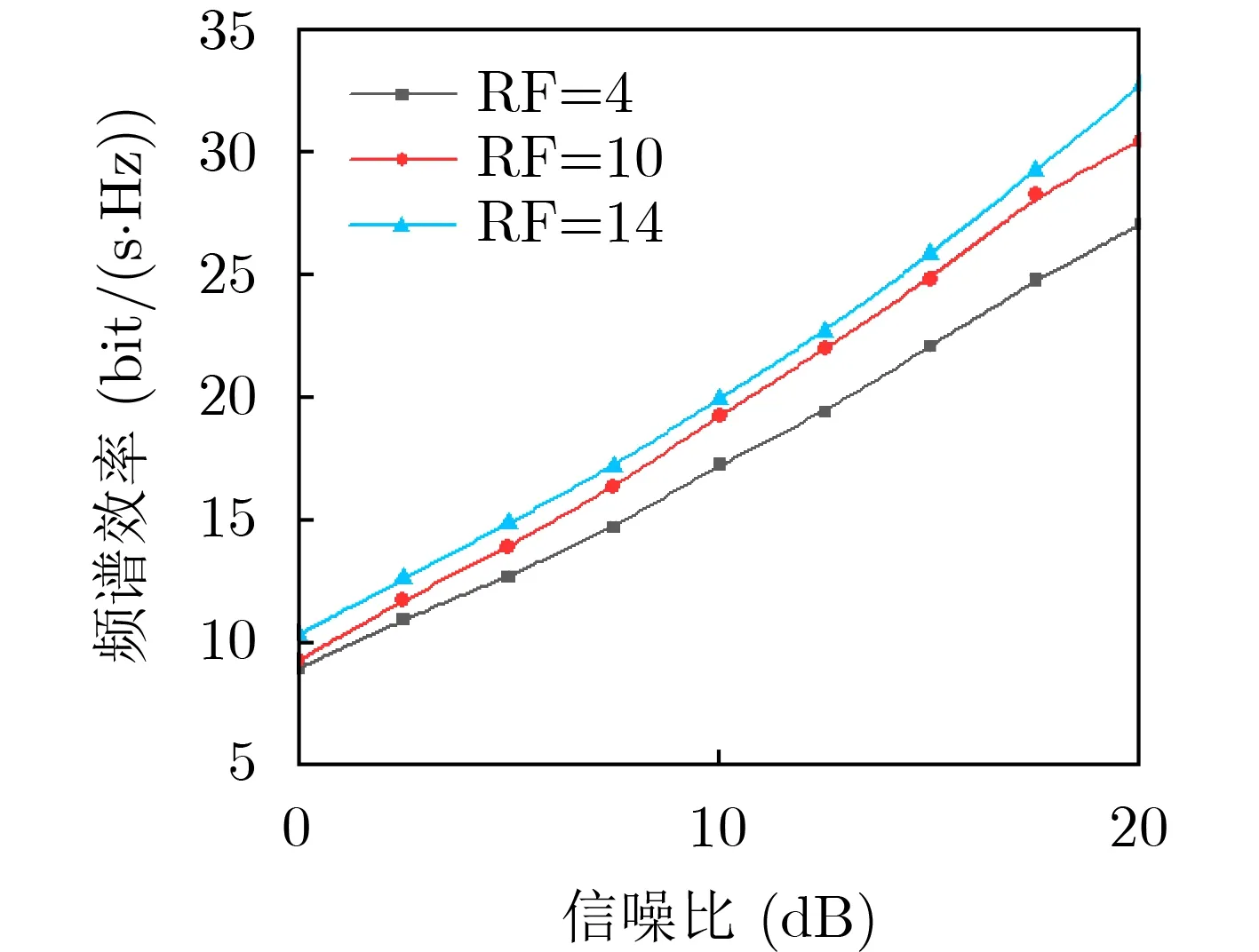
图6 RIS射频链数目对频谱效率性能的影响

图7给出了当RIS上元件数目为16,32,64时，对信道估计的归一化均方误差性能的影响。由图7可知，当RIS上元件数增加时，信道估计的性能在逐渐下降。这是由于当RIS上元件数增加时，其信道估计所需的参数也在增加，从而导致系统性能下降。而且当信噪比逐渐增加时，信道估计的性能也逐渐上升。这是由于当信噪比增加时，通信信道的状态良好，信道的估计性能提高。

图8和图9分别给出了当RIS上无源元件配置的射频链数目为8时，本文算法与现有ALS算法、ROOT-MUSIC算法、2D-FFT算法、2D-MUSIC算法的归一化均方误差和频谱效率系统性能的对比。由图可知，2D-MUSIC算法与本文算法的系统性能相近，而2D-MUSIC算法采用的是信号子空间与噪声子空间正交的性质得到信号的谱峰，需要更多的观测数据，更多的观测数据会导致导频开销增加。本文采用文献[12]中的2D-MUSIC算法仅使用了2D-MUSIC算法估计信道的角度参数，未采用其使用深度学习方法估计信道增益的方案。因为深度学习方法会带来更大的计算开销。2D-FFT算法由于信号的空间谱存在栅栏效应，采用信号补零方式以提高信道估计的精度，当信号补零后的维度增加时，信道估计的精确性进一步提高，但信号的维度增加，会增加信号的处理时间。为避免MUSIC算法的2维谱峰搜索，采用ROOT-MUSIC算法以多项式求根方式求解信道的角度参数，其角度估计精度较低。因此，本文所提算法可以提高信道估计的精确性，并且达到了系统性能和复杂度的平衡。

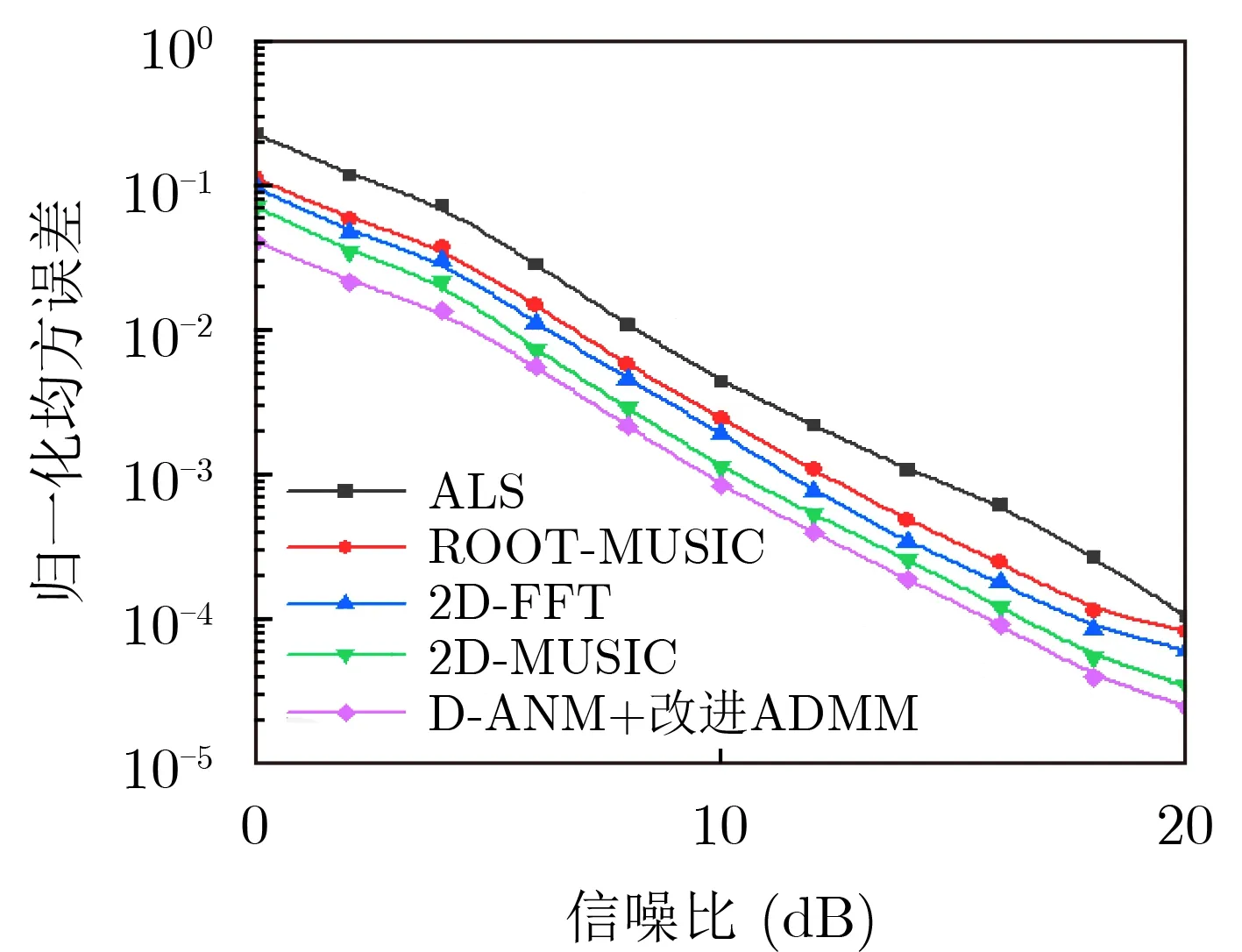
图8 本文算法与其他文献算法的归一化均方误差系统性能对比

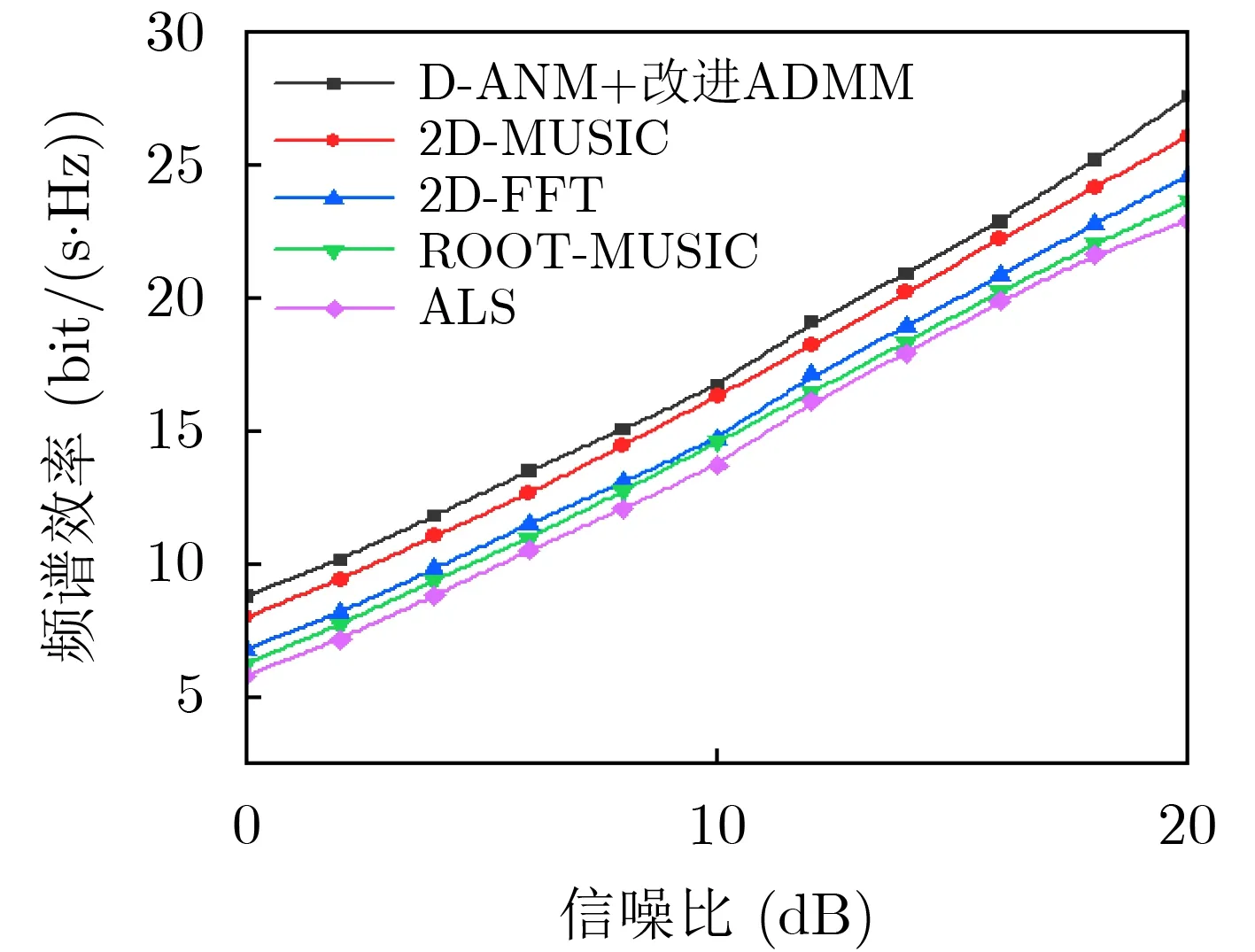
图9 本文算法与其他算法频谱效率性能对比

7 结论

本文针对RIS辅助的毫米波通信系统提出一种低复杂度的信道估计算法。通过在RIS部分的无源器件上配备射频链，以分离估计BS-RIS,RIS-UE的信道。所提算法首先通过解耦原子范数最小化将信道的离开角和到达角2维角度估计问题解耦为两个1维的角度估计问题，其次采用动量梯度下降法避免ADMM算法中信道矩阵参数更新时的矩阵求逆运算，并通过联合优化迭代步长和信道参数，提高信道参数的估计精度，最后根据角度参数和信道矩阵参数获得信道路径增益。通过仿真实验验证本文所提算法在保持较低复杂度的同时提高了系统的信道估计性能。