低信噪比场景下Link-16系统的联合频偏估计算法
2023-11-18宁晓燕罗海玲孙志国
宁晓燕 罗海玲 孙志国 刁 鸣
(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)
1 引言
数据链常用于军用无线通信场景,是使作战平台能够快速获取信息的重要技术。为满足作战场景的高标准与高要求,收发平台需要考虑数据链通信环境的复杂性,保证收发双方的话路畅通、通信的高效实时性和保密性。由于Link-16数据链是目前最完善,且应用最为广泛的数据链,故本文以Link-16数据链为背景展开研究。Link-16作为一种军用通信系统,被用于高速移动武器平台时,其终端载体飞行速度每秒可达几千米,高速运动使得Link-16系统传输的数据帧之间存在较大的多普勒频移。根据多普勒频移的计算公式fd=fc·v/c,多普勒频移fd除了与运动速度v有关,还与信号的载频fc相关。Link-16系统的通信载频在L波段(即1~2GHz),高于其他许多常见的通信载频。Link-16数据链不仅需要面对多变的作战环境影响,还要面对复杂的多普勒效应,因此,如何更有效地对Link-16信号进行频偏估计,实现信号的准确接收成为通信交互过程中获取信息的关键。
现有公开资料中,专门针对Link-16数据链信号的多普勒频移解决方法较少,故文章主要参考了卫星通信与高铁信号传输等场景所涉及的多普勒效应解决方法。对于多普勒效应导致的频率偏移,常用的估计方法主要分为数据辅助方法(Data-A ided m ethod,DA)、非数据辅助方法(Non-Data-A ided method,NDA)和判决引导方法(Decision-Directed method,DD)。相较于DA算法而言,NDA和DD算法的信噪比门限较高,不适用于高速猝发通信[1],而Link-16数据链一个时隙长度仅为7.812 5 m s,故本文利用DA算法进行设计分析。文献[2–5]提出了4种经典的频偏估计算法——Kay算法、Fitz算法、L&R算法与M&M算法,Kay算法复杂度低,估计范围大,但对信噪比门限要求较高,Fitz算法与L&R算法能在较低信噪比条件下接近克拉默-拉奥界(Cramer-Rao Bound,CRB),但对于大多普勒频偏不敏感,M&M算法接近于理想估计范围,但频率较大时信噪比门限会快速变差。文献[6]在Kay算法和L&R算法基础上提出一种两步频偏估计算法,能有效提高估计精度但主要是对多径衰落下的增强遥测综合网(integrated Netw ork Enhanced Telemetry,iNET)系统进行研究。文献[7]也采用了两步频偏估计算法,考虑了估计精度与复杂度的平衡。文献[8]提出一种正交角域子空间投影算法,将高动态多普勒频散投影到每个正交子空间,利用正交子空间的等效多普勒频移进行估计。文献[9]提出一种改进的Link-16标准双脉冲封装格式(STandard Double Pulse,STDP),在STDP时隙结构的基础上,在不发送信息的2×6.6μs中插入导频序列,以便于接收端的频率估计,但文中未考虑跳频在系统中到的应用,且主要研究多径衰落下的信道估计。文献[10]针对稀疏码多址接入(Sparse Code M ultip le Access,SCMA)系统提出一种DA载波同步方案,算法结合了自相关算法、L&R算法以及互相关算法对多普勒频偏进行了分步估计,并对导频数据的分布图样进行了优化,能达到较为理想的误码效果,但同时多种算法的应用带来了较大的时间开销。文献[11]提出一种基于梳状解调参考信号的联合频偏估计方法,利用时域相关与频域相关来提高估计精度、提升系统性能,但该方法主要应用于5G通信场景,且估计范围有限,仅在[–1.5 kHz,1.5 kHz]范围内的估计精度较高。上述大多研究是基于信噪比较高的电磁环境展开,或是仅从频域或时域出发。从频域出发研究需重点考虑频域变换点数多带来的问题(如复杂度和栅栏效应),从时域出发研究则通常受到估计范围和信噪比门限的影响。
本文结合Link-16数据链的信号结构特征,对时隙布局进行重分配,推导了该结构下的克拉默-拉奥下界(Cramer-Rao Low Bound,CRLB),并在此基础上提出一种适用于低信噪比条件下的联合频域变换与时域相关的数据辅助型频偏估计算法,本算法综合考虑了时域与频域两方面的问题,致力于在所设计的信号帧格式基础上实现一种平衡,达到改善估计精度、估计范围与信噪比门限三者矛盾的目的。所提算法在保证Link-16系统适应较大多普勒频移前提下,提高了估计精度,在Link-16数据链系统中具有较强的实用性。
2 Link-16系统模型
2.1 模型描述
本文以STDP消息格式进行讨论,该格式下的信息包含258个脉冲信号,设a n(t)为第n个脉冲编码后的符号数据,cn(t)为 其对应的扩频序列,d n(t)为该脉冲经扩展后的信号
其中,n=1,2,...,len,l en为编码后的信息总长度,扩频序列为32 bit码片。Link-16系统采用最小频移键控(M inimum Shift Keying,MSK)调制和跳频,跳频频段为969~1008MHz,1053~1065 MHz和1113~1206 MHz,各频段跳频点分布个数分别为14,5,32,跳频图案如图1所示。
系统按照跳频图案随机选择51个频率作为MSK调制载波频率[12],进行跳频。则调制后的信号为
其中,dni与dnq为dn经差分编码和串并转换后的上下支路信号。f n为第n个脉冲的跳频频率;Ts为MSK信号的符号周期;φn为第n个码元的相位常数。接收端收到的Link-16信号表示为
其中,K为脉冲数目;r ect(·)为 矩形窗函数;TH是一跳持续时间;f dn是第n个脉冲信号由于接收机与Link-16运载终端之间高速运动产生的多普勒频偏;θn是第n个脉冲的初始相位。n(t)是均值为0,方差为σ2=N0/2的加性高斯白噪声。
2.2 基于导频序列的时隙结构设计
为避免造成过大的冗余、降低信息传输速率,本文考虑将导频序列插入到Link-16的标准双脉冲时隙结构中不发送任何信息的2×6.6μs上,用于接收端的频率估计。加入导频后的时隙结构和脉冲结构如图2、图3所示。

图2 加入导频序列的时隙结构
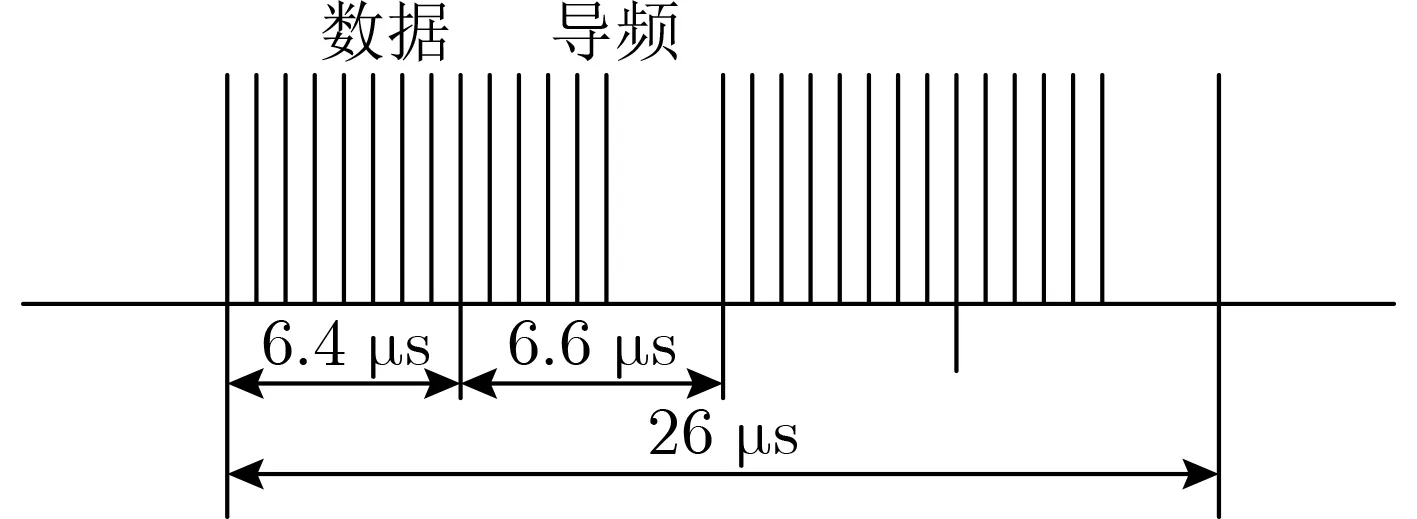
图3 加入导频序列的脉冲结构
这种设计方式不占用额外带宽,在通信过程中能减小对系统效率的影响,避免冗余信息带来的额外时间开销。
3 频偏估计算法
3.1 基于改进数据帧结构的克拉默-拉奥下界(CRLB)推导



3.2 联合频域变换与时域自相关运算的分步式频偏估计算法
接收端从接收信号中提取导频信号,为方便研究,以一个脉冲为例进行分析
其中,p(t)为导频符号序列。假设系统具有理想的符号定时,则y(t)经匹配滤波和采样得到
其中,m=1,2,...,L-1;L为导频序列的长度。假设p(k)p*(k)=1,n(k)是实部与虚部相互独立的复值加性高斯白噪声样本。
分布式频率估计算法分为频率粗估计与频率细估计两步。本文频率粗估计采用相关函数的频域变换,首先对大多普勒频偏进行捕获,再利用粗估计得到的频偏对接收信号进行补偿,最后通过细估计中改进的L&R算法捕获对剩余频偏进行估计,得到剩余频偏估计值来补偿信号,该方法结合了时域相关与频域变换,时域相关算法对信噪比的高要求与频域变换多点数带来的额外开销相互平衡。算法的实现流程如图4所示。
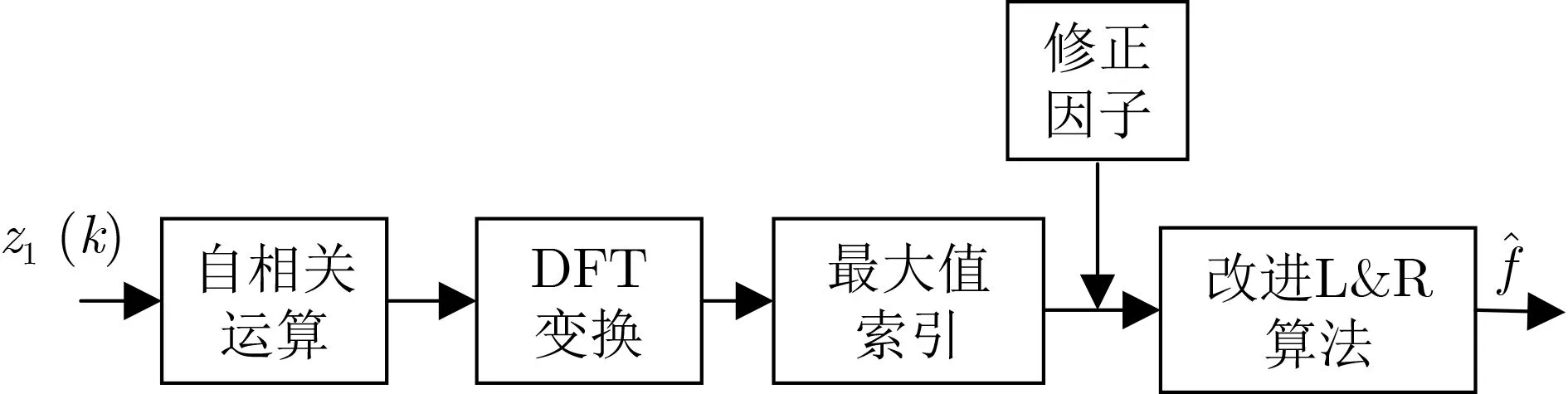
图4 所提算法实现流程图
对于DA算法,为避免导频幅度的影响,需要进行去调制操作。即对式(15)左右同乘p*(k),得到

其中,δ为修正因子;R e[·]表示取实部[13]。由此得到频率粗估计值
为降低算法的估计的信噪比门限,此处采用L&R算法进行频率细估计,L&R估计算法表示为[14]
其中,N为平滑噪声系数,取值范围1≤N ≤L。R′(m)为粗估计补偿信号z2(k)的自相关函数。为消除相关函数的量级扩散,本文对L&R算法做出改进,将相关函数的和值进行标准化,使其具有单位量级,从而获得更低的估计值方差[15,16],即
由于跳频影响,信号在传输过程中会受到不同程度的多普勒频率偏移,因此接收端对多个脉冲做并行分步频偏估计算法,得到每帧信号的频率偏移量,最后对信号进行补偿,以提高信号解调的准确率。经频偏估计值补偿后的信号表示为
4 仿真与结果分析
本文在消息格式为STDP的Link-16系统下进行仿真,系统编码采用CRC-12校验码和RS(31,15)编码,组网方式为TDMA。为保证仿真的实际性与可信度,文章严格按照Link-16数据链的物理层结构与空间信道规则进行蒙特卡罗仿真实验。
图5分别给出了在加性高斯白噪声(Addictive W hite Gaussian Noise,AWGN)信道和多普勒频移(Doppler Frequency-offset Shift,DFS)信道下系统的误码率曲线。信噪比范围为–2~10 dB,终端飞行速度为3.4 km/s。相关参数配置如表1所示。
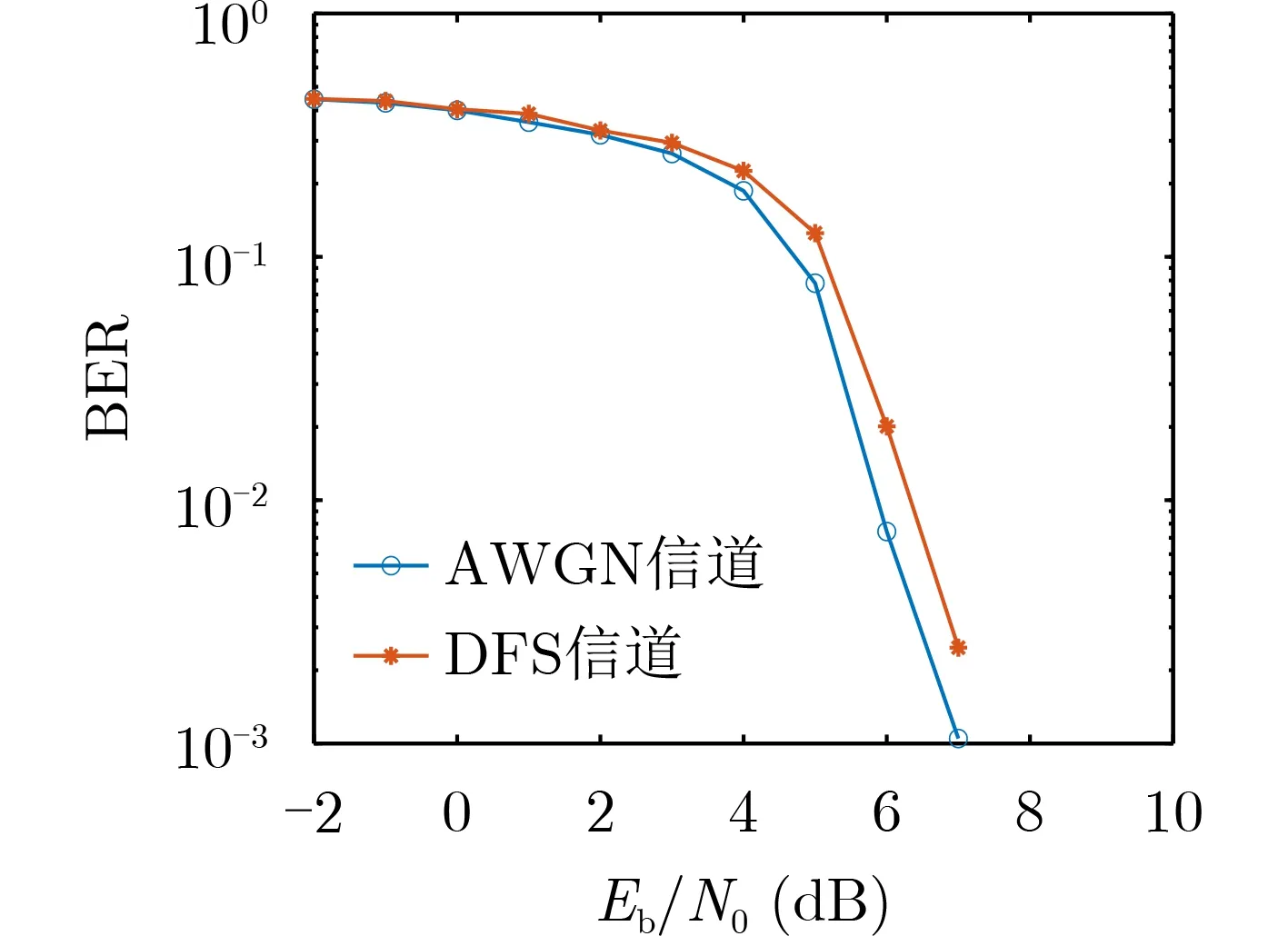
图5 不同信道下误码率曲线
从图5仿真结果可以看出,当信噪比为7 dB时,AWGN信道下的系统误码率为10–3,DFS信道下的误码率约为2×10–3,多普勒效应的存在使误码率增大了1倍。图6对Link-16信号在不同运动速度下的误码率曲线进行了仿真。

图6 不同飞行速度下的误码率曲线
图6为不同飞行速度在多普勒效应下的系统误码率,由图可见,3.4 km/s和6.12 km/s的误码率差值可达1个量级,参考现有资料,数据链飞行终端速度可高达6.8 km/s,且伴随一定的高阶变化率,因此多普勒效应造成的影响不可忽略。
4.1 估计精度分析
算法的估计效果用均方误差(M ean Square Error,MSE)来衡量,即
其中,M为蒙特卡罗实验仿真次数。
将本文算法与Fitz算法、L&R算法与改进L&R算法进行仿真分析,频率偏移量fdT s=0.002时,各算法的MSE曲线如图7所示。
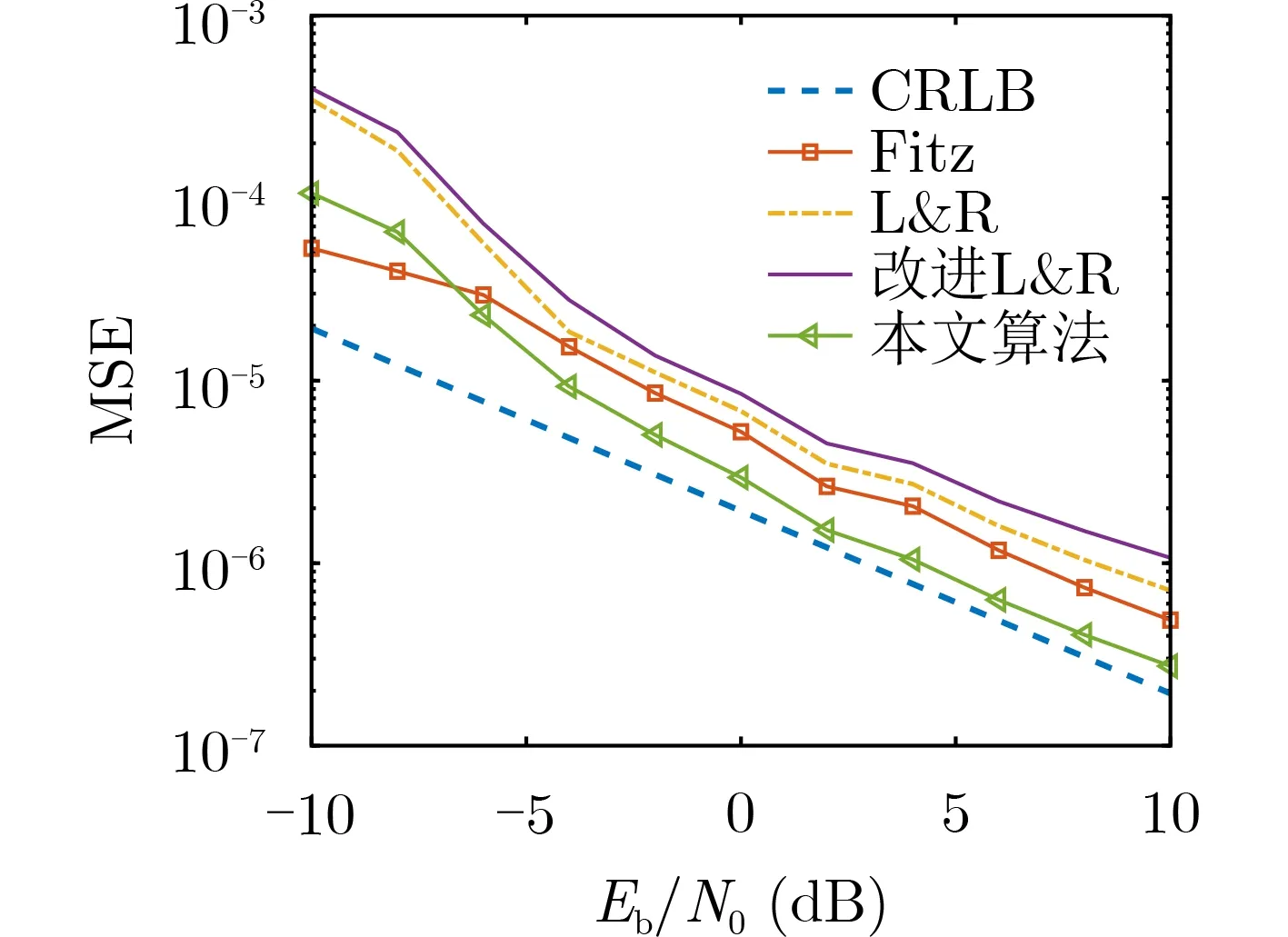
图7 不同估计算法的均方误差
图7结果显示,由于利用了相距较远的采样点的相位差,且为消除量级扩散,文章所提算法对自相关函数做了和值的归一化,信噪比小于–8 dB时,Fitz算法的MSE相对更低。而在相同的频偏下,信噪比在–8~10 dB范围内,本文所提算法均方误差更低,更接近实际多普勒频偏量,且随着信噪比增加,所提算法的MSE逐渐趋近CRLB,说明该算法具有较高的估计精度。
4.2 估计范围分析
图8给出了信噪比为0 dB时不同频偏下,5种常见估计算法与本文所提算法的MSE曲线。
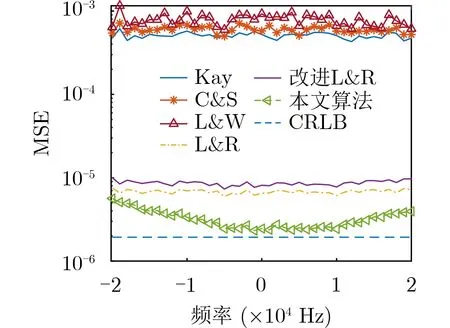
图8 不同估计算法的估计范围
从图8可以看出所提算法在数据链传输场景下的频偏范围,即[–20 kHz,20 kHz]中估计精度接近于10–5。
4.3 估计效果分析
为验证所提算法的补偿效果,本文仿真了理想多普勒场景与5.1 km/s飞行速度下该算法进行多普勒频偏补偿后的系统误码率。仿真结果如图9所示。
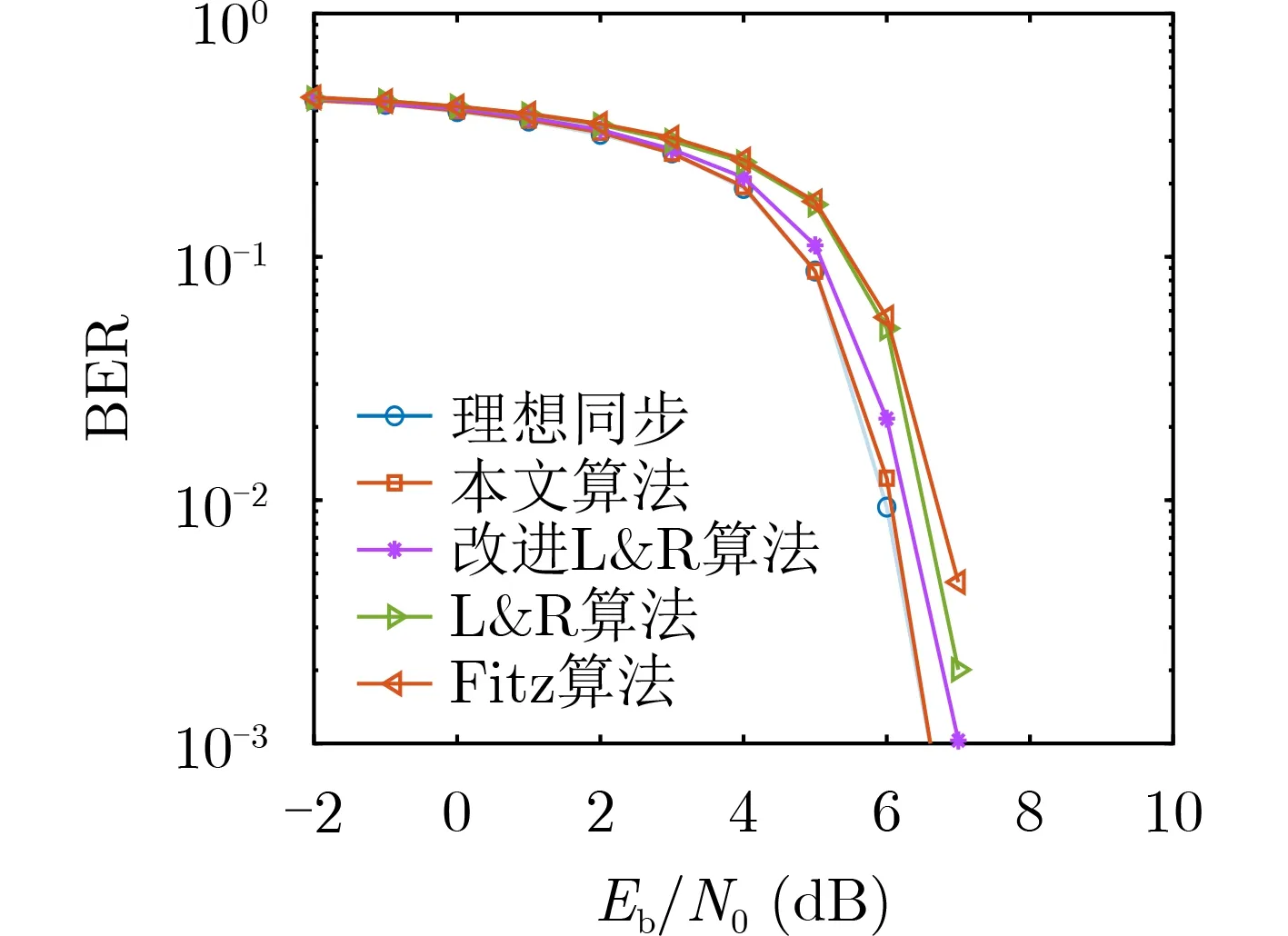
图9 接收系统误码率
由图9可以看出,当信噪比为6.5 dB时,本文所提算法的误码率曲线与理想载波同步的误码率曲线几乎重合,且明显优于其他3种算法,由此说明在信噪比较低的情况下,应用本文所提算法对接收信号进行估计补偿能够获得更为理想的效果。
5 结论
本文对Link-16信号的多普勒效应进行了研究。考虑低信噪比场景下Link-16数据链系统中存在大动态多普勒频移的问题,本文设计出一种新的导频数据结构,并在此基础上提出一种联合时域和频域的分步式频偏估计算法。本算法在复杂度上略高,但能在不占用额外频谱资源的前提下提高系统的频偏估计精度,同时能获得较大的估计范围。仿真结果显示,本算法提升了Link-16系统的误码性能,对数据链研究具有较高的应用价值。
