一种新型大转角弱耦合并联髋关节外骨骼的设计及分析

2023-11-17徐继龙刘福才牛云展

中国机械工程 2023年21期

徐继龙刘福才牛云展

1.燕山大学智能控制系统与智能装备教育部工程研究中心,秦皇岛,0660042.燕山大学工业计算机控制工程河北省重点实验室,秦皇岛,0660043.燕山大学机械工程学院,秦皇岛,066004

0 引言

髋关节外骨骼作为外骨骼中的一类典型产品,通过向下肢传递动力来辅助人体进行运动和康复训练,可有效提高髋关节的运动能力,延缓髋关节生理机能衰退,逐渐成为研究热点。

从机构类型来看,髋关节外骨骼可分为串联式和并联式两大类。串联髋关节外骨骼的优点是结构简单、控制容易,但存在人机转动中心错位的问题。人机转动中心错位引起人机之间产生不可控的交互力,导致穿戴者运动不适、疼痛甚至受伤[1]。为避免人机转动中心错位,常用的解决办法有两种:①在外骨骼和肢体连接部位引入柔性绑带/卡套[2-3];②增加外骨骼的自由度[4-6]。第一种方法简便易行,但只能补偿广义上的人机轴线偏差,无法实现外骨骼在关节层级对肢体的精确助力控制,仅适用于助力精度要求不高的场合[7]。第二种方法在在一定条件下可使外骨骼在关节层级实现对肢体的精确助力控制,但存在如下弊端:①增加主动自由度会增大外骨骼的制造成本及控制难度;②增加被动自由度会导致外骨骼自身位置存在不确定性,且被动子链过长会降低人机运动的协同性[8]。

并联髋关节外骨骼可分为仿生式与生物融合式两类。仿生式并联髋关节外骨骼具有3个转动自由度,如3-RRR[9]。这类外骨骼虽然能在一定程度上辅助腿部运动,但其转动中心与髋关节中心并不重合,人机之间容易产生交互力,使得助力效果不理想,因此少数研究者采用生物融合的理念对髋关节外骨骼进行设计[10-12]。根据主动自由度数量可将这类外骨骼分为主动自由度小于3和主动自由度等于3的外骨骼。前者仅能提供一两个方向的助力,无法满足髋关节任意方向的康复训练需求。后者虽能具有足够的主动自由度,但通常存在以下不足:①工作空间较小,无法实现大范围的康复运动;②具有强耦合特性,即输入与输出的关系呈高度的非线性,这导致外骨骼建模和运动控制非常困难;③部分电机安装在一个活动架,增加了外骨骼的转动惯量。

为解决上述问题,本文设计出一种并联髋关节外骨骼,从根本上解决人机转动中心错位的问题。该外骨骼具有较大的工作空间,在屈曲/伸展方向上具有弱耦合特性,在内收/外展方向上具有解耦特性,降低了外骨骼的控制难度,且所有电机均安装在一块固定板上,转动惯量低、灵活性好。

1 髋关节外骨骼设计

下肢运动过程中,髋关节的屈曲/伸展、内收/外展和内旋/外旋运动分别主要用于前行、保持身体平衡和改变运动方向[13]。因此,为全方位满足髋关节的康复运动需求,所设计的髋关节外骨骼应能够提供3个转动方向的助力。

1.1 髋关节外骨骼简介

图1 髋关节外骨骼虚拟样机

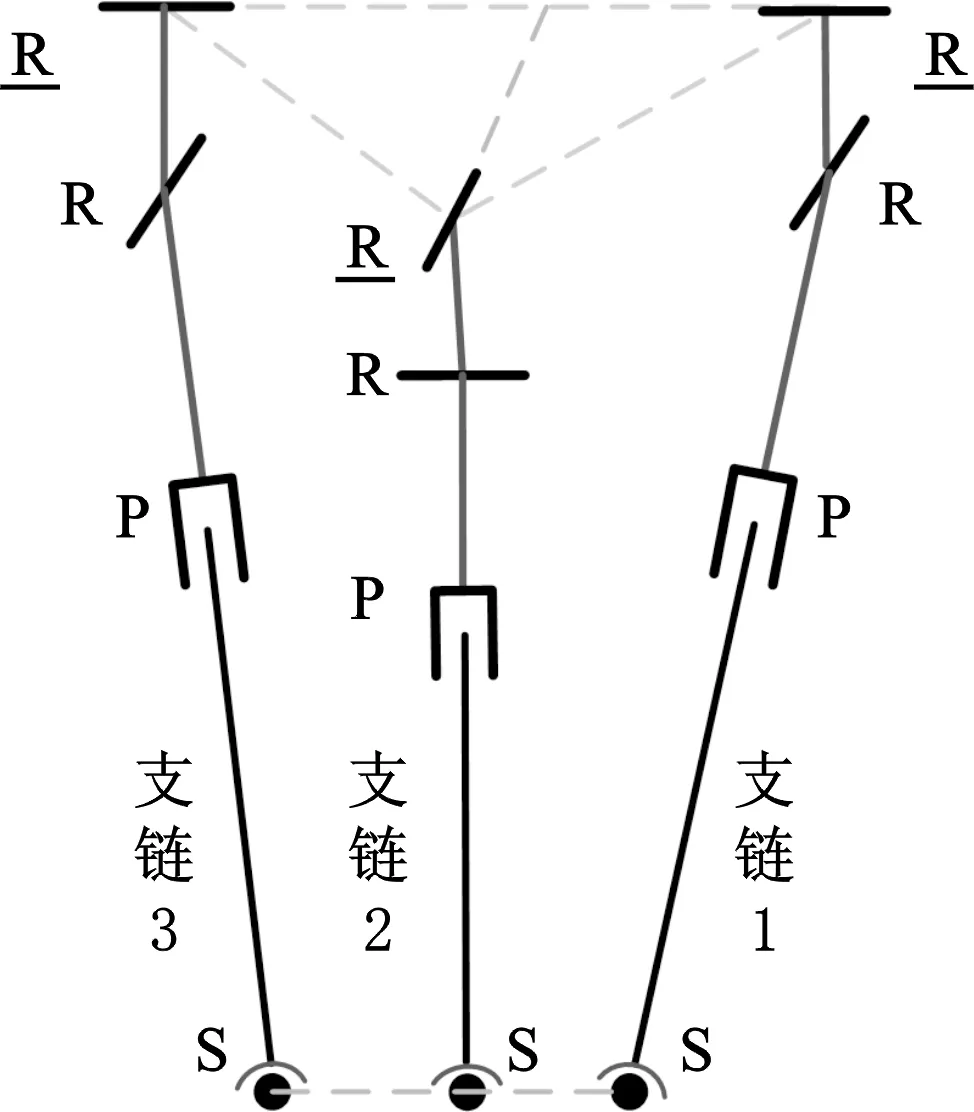
图2 髋关节外骨骼的构型简图

1.2 二级移动副结构设计

髋关节外骨骼移动副的伸缩范围是影响工作空间的主要因素。常规的从动式移动副由一组导套和导杆组成,其行程由导套和导杆的长度决定,此类产品行程占比(行程/最短长度)较小,很难满足狭小空间的使用需求。为减小外骨骼的设计尺寸,增大外骨骼的活动范围,设计出一种从动式二级移动副。该移动副由导套组件、一级杆组件、二级杆组件、弹簧组件1和2构成,如图3所示。

图3 二级移动副设计方案

二级移动副内部组件的伸长顺序为二级杆组件先伸长,一级杆组件后伸长;缩短顺序为一级杆组件先缩短,二级杆组件后缩短。一级、二级杆组件运动到某一位置时,将受弹簧组件的约束。假设二级移动副2个弹簧组件的弹性模量相同,则一级、二级杆组件的伸缩顺序由其楔形槽坡面角度决定。二级移动副在竖直状态下最易伸长、最难缩短,故在此状态下对坡面角度进行设计。

为方便分析,定义靠近定平台一侧坡面为U侧坡面,靠近动平台一侧坡面为D侧坡面。下面分别对U侧和D侧坡面角度进行设计计算。

1.2.1U侧坡面角度设计

(a)杆组件z向受力 (b)弹簧组件x向受力

弹簧组件i静力平衡时,可得

(1)

G1=m1g+m2gG2=m2g

(2)

(3)

1.2.2D侧坡面角度设计

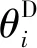
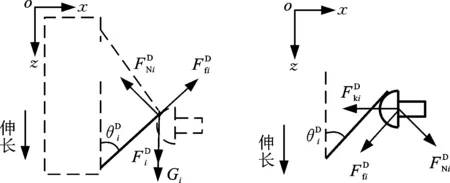
(a)杆组件z向受力 (b)弹簧组件x向受力

弹簧组件i处于静力平衡时,可得

(4)

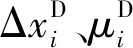
(5)

(6)

(7)

综合考虑弹簧型号、加工精度、负载等情况,对相关参数进行合理赋值,并将其代入式(3)、式(6),得到U侧和D侧坡面的角度。

2 人-机复合体的运动学分析

2.1 自由度分析

根据Kutzbach-Grübler自由度计算公式,可得并联机构的自由度

(8)

式中,M为机构自由度数;n为构件数;s为运动副数;fi为第i个运动副的自由度数。

2.2 位置逆解

如图6所示,在A点建立固定坐标系AXYZ(简称“{A}”),在B点建立动坐标系Bxyz(简称“{B}”)。规定人体下肢直立时,人-机复合体所处位姿为初始位姿,该位姿下动平台与定平台平行,且{A}和{B}的坐标轴指向一致。令sij、θij分别为支链i(i=1,2,3)中转动副j(j=1,2)转动轴线的方向向量和转动角度,l1为Ci1Ci2的长度,a为AC11和AC31的长度,b为AC21的长度,r为BC13和BC33的长度,ψ为BC13与BC33的夹角(为布置美观,取ψ=60°),li2为支链i中P副的杆长。在初始位姿下,B点在{A}中的坐标为(0,-c,h),O点在{A}中的坐标为(xo,yo,zo)。

本文选用Z-Y-X欧拉角描述动平台的姿态变化。假设动平台绕X轴、Y轴和Z轴的转动角度分别为α、β和γ,则动平台相对于定平台的旋转变换矩阵为

sw=sinwcw=cosww=α,β,γ

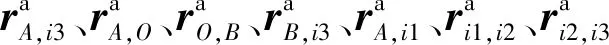
(9)

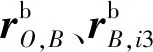
(10)

(11)

(12)

联立式(9)～式(12)求得

(13)

a1=xo-0.5ra2=-xoa3=xo+0.5r

2.3 位置正解

s11=sin(θ11+φ1)c11=cos(θ11+φ1)

c21=cosθ21s31=sin(θ31+φ3)

c31=cos(θ31+φ3)

Lic=l1+li2cos(φ′i+θi2)

(14)

由式(14)可求得人-机复合体的位置正解:

(15)

式(15)有3个中间变量Lic(i=1,2,3),每个Lic均包含一个li2和θi2,这6个未知变量满足以下约束方程组:

(16)

根据式(16),进一步得到下式

(17)

p1=yos11-zoc11

p2=xos21+zoc21

p3=yos31-zoc31

当外骨骼只进行屈曲/伸展运动时,将β=0,γ=0代入式(13),得到如下关系:

(18)

w1=(b1tan(θ11+φ1)-c1)2

w2=(c1tan(θ11+φ1)-b1)2

由式(18)可知,人腿在进行屈曲/伸展运动时,支链1和支链3的电机以相同的角度变化规律进行转动,支链2的电机未发生动作,此时的外骨骼具有弱耦合特性。

(19)

v1=[(c1cα-b1sα)tanθ21+x0]2

v2=(x0tanθ21+b1sα-c1cα)2

由式(19)可知,外骨骼前屈α0进行内收/外展运动时,支链1和支链3的电机未转动,支链2的电机以某一规律转动,此时的外骨骼具有解耦特性。

2.4 逆雅可比矩阵

速度雅可比矩阵是并联机构运动学性能分析的基础。对比位置正、逆解可知,逆雅可比矩阵J-1更加容易求解。将式(13)两端对时间进行求导,得到动平台的欧拉角速度与电机角速度的关系。进而,根据动平台的角速度与欧拉角速度的关系得到雅克比矩阵J-1,如下:

式中,Eij为矩阵E中第i行第j列的元素,j=1,2,3。

3 人-机复合体的工作空间分析

人-机复合体的结构参数如表1所示。

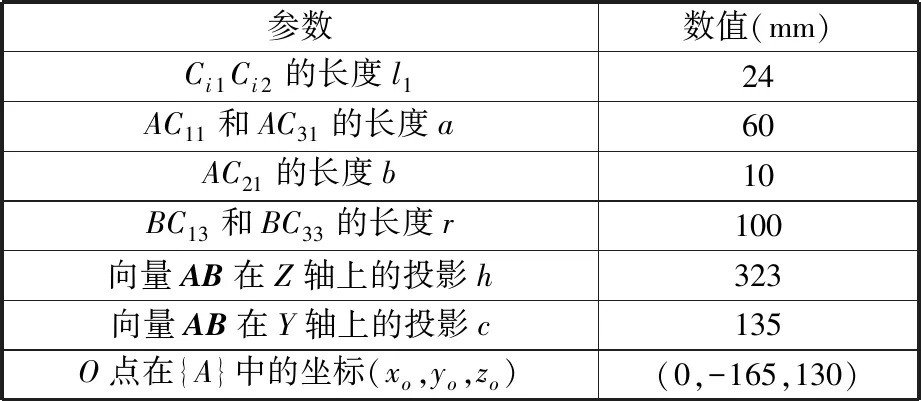
表1 人-机复合体的结构参数

限定各移动副杆长变化范围为176 mm≤li2≤376 mm,球副的转动角度范围为-30°～30°。设定搜索范围为-60°≤α≤60°、-60°≤β≤60°、-60°≤γ≤60°。通过数值搜索法,绘制髋关节外骨骼的工作空间,如图7所示。

由图7可知,人-机复合体的工作空间是连续的实心多面体;从若干方位来看,它可以达到设定的极限搜索边界。α=0°时,动平台在内收/外展和内旋/外旋运动方向上均能在-60°～60°范围内运动;β=0°时,动平台在内旋/外旋运动方向上可实现-60°～60°的运动,在屈曲/伸展运动方向上可实现-45.0°～31.5°的运动;γ=0°时,动平台在内收/外展运动方向上可实现-60°～60°的运动,在屈曲/伸展运动方向上可以实现-44.5°～31.5°的运动。显然,人-机复合体的工作空间具有较大的转动范围,远大于人体髋关节日常行走运动范围[14],故本文设计的髋关节外骨骼可满足下肢助力行走运动需求。

4 人-机复合体的性能分析

4.1 灵巧性分析

(20)

(21)

将式(20)、式(21)联立,得

(22)

(23)

式中,‖J‖‖J-1‖为雅可比矩阵的条件数。

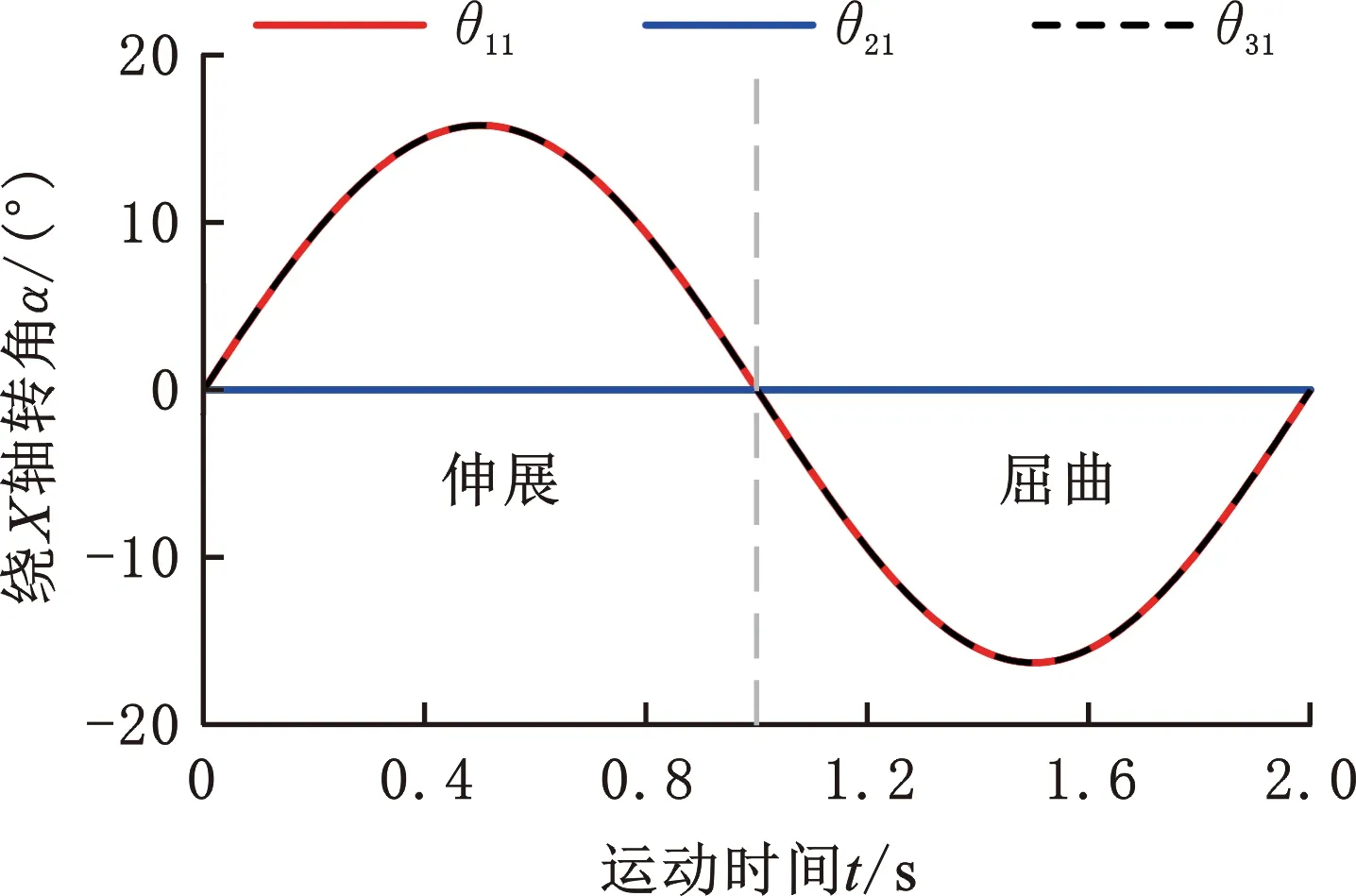
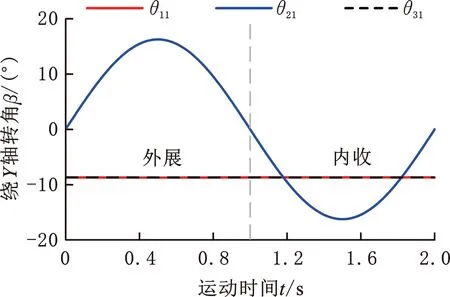
条件数的倒数K=1/(‖J‖‖J-1‖)可作为灵巧度指标来衡量机构的灵巧性[15]。0

在规定工作空间内,对人-机复合体的灵巧度K进行求解,分别绘制全域、α=0°、β=0°、γ=0°时的灵巧度图谱,如图8所示。

(a)全域灵巧度图谱

由图8可知,K的范围为[0.14,0.22],且K随α增大而增大,随着β和γ绝对值的增大而减小。在全域范围内,K变化趋势相对平缓、没有突变,这表明人-机复合体在工作空间内无奇异位形,具有较好的运动灵活性。根据全域内K的取值范围可知,人-机复合体的灵巧度各向异性程度接近于髋关节运动所需驱动力的各向异性程度,说明外骨骼构型设计合理。

4.2 力矩传递性能分析

令M和τ分别表示动平台所受外力矩和关节驱动力矩,根据虚功原理可知

M=(J-1)Tτ

(24)

由于人体在行走过程中,髋关节以屈曲/伸展运动为主,故本文定义单位驱动力矩作用下动平台绕X轴的输出力矩为局部力矩传递指标

TM=|(J-1)Tf|

(25)

式中,f表示JT的第一列向量的单位向量。

TM只能反映特定位姿下的力矩传递能力,故本文定义TM在全域工作空间内的平均值为全域力矩传递指标,即

(26)

式中,W表示全域工作空间。

在规定工作空间内对人-机复合体的力矩传递性能进行仿真分析,分别绘制全域、α=0°、β=0°、γ=0°时的局部力矩传递性能图谱,如图9所示。

(a)全域内局部力矩传递性能图谱

由图9可知,人-机复合体的局部力矩传递性能TM的范围为[0.58,0.83],全域范围内,TM变化趋势比较平缓均匀。β和γ不变时,随着α由-40°逐渐变化至10°,TM逐渐减小;α不变时,TM随β和γ绝对值的增大而减小。由图9a可知,屈曲/伸展角度越大,人-机复合体的力矩传递能力越强,且在较大屈曲/伸展角度下,外骨骼进行内收/外展和内旋/外旋运动时均能提供较大的力矩传递能力。此外,根据式(26),求得IT为0.78,这说明人-机复合体在全域内的平均力矩传递能力也较好。

4.3 运动耦合性分析

当人的大腿以y=30°sin πt规律分别做周期性的屈曲/伸展和内收/外展运动时,得到各电机角度的变化规律如图10、图11所示,其中,T为运动周期。

图10 屈曲/伸展运动时各电机角度规律

图11 内收/外展运动时各电机角度规律

由图10可知,支链1和支链3的电机以相同规律转动,支链2的电机未转动,这表明外骨骼在屈曲/伸展运动方向上具有弱耦合特性。由图11可知,支链1和支链3的电机仅在大腿抬起时顺时针转动8.7°,在内收/外展运动下未发生转动;支链2的电机在大腿抬起时未转动,仅在内收/外展运动下周期性转动,这表明髋关节前屈16.2°(由α0计算所得)进行内收/外展运动时,外骨骼具有解耦特性。上述结果与位置正解分析一致,说明位置正解建模正确。

相比现有的并联髋关节外骨骼,本文所提外骨骼具有独特的运动弱耦合特性,这使其运动学和动力学建模相对简单,求解模型所用时间较短,对电机的实时控制有利。另外,在屈曲/伸展运动方向上,由对称布置的2条支链同时提供同向且数值相近的助力,这有利于选择小型的电机,减小外骨骼的重量及能耗。由于所提外骨骼具有较大的活动范围及良好的力传递性能,其应用不仅限于助力行走,也可用于髋关节运动康复。在髋关节内收/外展运动康复中,外骨骼的运动解耦特性会使其控制更加容易。