一种基于动态残差的自适应鲁棒无迹卡尔曼滤波器定位算法

许 万 程 兆 夏瑞东 陈汉成

1.湖北工业大学机械工程学院,武汉,4300722.深圳海外装饰工程有限公司,深圳,518031

0 引言

放线是完成建筑装饰的基准线,对精度要求极高。相对于应用在制造业、仓储业的移动机器人,智能移动放线机器人对轨迹跟踪精度的要求极高,高定位精度和快速跟踪自身位姿是实现高精度轨迹跟踪的基础。由于环境噪声的存在,测量位姿与真实位姿之间存在偏差,而且智能移动放线机器人工作的实际建筑施工现场为未整平的水泥地面,存在大量不规则分布的凹陷和凸起障碍物,具有很强的非线性,传统定位算法无法满足精度要求。

对于非线性系统的定位算法,卡尔曼滤波器[1](Kalman filter,KF)并不适用,常用于非线性系统定位的滤波算法有拓展卡尔曼滤波[2](extended Kalman filter,EKF)、粒子滤波[3](particle filter,PF)和无迹卡尔曼滤波[4](unscented Kalman filter,UKF)等。系统为强非线性系统时,EKF的精度较差,且预测函数中的参数较多时,其雅可比函数比较复杂、运算量巨大、实时性较差[5]。对于非线性系统的定位问题,PF具有较高的精度,但需要大量的样本,且机器人面临复杂情况时的算法复杂度高、计算量大[6]。相较于EKF,UKF具有更高的精度和稳定性。相较于PF,UKF具有更小的计算量和更好的实时性[7]。UKF需要提前建立目标的状态方程并预设固定噪声,而系统在实际运行过程中的噪声往往会不断变化,且不与预设噪声相同,因此UKF无法满足智能移动放线机器人对精度的要求,并且预测过程中可能出现预测位姿信息发散的问题。智能移动放线机器人对实时定位要求极高,UKF算法却无法满足实时性的要求。

针对UKF在定位中存在的问题,研究者提出了许多改进的UKF算法,LIU等[8]结合UT变换与EKF算法,提出了一种UEKF算法。相较于UKF算法,该算法的运算速度得到极大的提升,但准确率与鲁棒性几乎没有提高。文献[9-10]利用次优Sage-Husa噪声估计器对系统的噪声统计特性进行实时更新,获取了更强的鲁棒性,但定位过程中存在预测位姿信息发散的可能。 MENEGAZ等[11]提出了一种新的最小sigma集提取方法,减少了UKF算法的运算量,在一些特定情况下可以获得更高的运算速度,但算法的运用存在一定局限性。肖磊等[12]引入自适应矩阵来修正系统噪声协方差,提高了UKF算法的鲁棒性,但该方法需要提前估计系统状态,增大了系统运算量。

为满足智能移动放线机器人目标实时定位和目标位姿状态准确估计的要求,本文提出了一种基于动态残差的自适应鲁棒无迹卡尔曼滤波(adaptive robust unscented Kalman filter,ARUKF)算法。针对存在复杂外部干扰的系统扰动问题,结合UKF与抗差估计理论,利用滤波过程中的动态残差来减小系统扰动对位姿信息预测的影响。可以根据动态残差计算自适应加权因子,实时对预测矩阵和误差协方差进行加权处理,减小环境因素对系统稳定性的影响,提高定位精度和鲁棒性,同时通过采样优化来减小系统运算量、提高系统实时性。仿真与实物实验验证了算法的可行性。

1 运动学模型及定位系统

1.1 智能移动放线机器人的运动学模型与状态方程

本文研究的智能移动放线机器人是双轮差速式移动机器人[13]。图1所示的机器人运动学模型中,大地坐标系为OXY,将机器人前驱轮轴线的中心点OR定义为机器人的运动学中心,建立机器人的局部坐标系ORXRYR。

图1 智能移动放线机器人运动学模型

智能移动放线机器人的位姿为(x,y,θ)T,其中,(x,y)为机器人运动学中心在全局坐标系中的坐标,θ为机器人局部坐标系XR轴正方向与全局坐标系X轴正方向之间的夹角。智能移动放线机器人的运动状态可由矢量U=(v,ω,a)T表示,其中,v、ω、a分别为机器人运动学中心的速度、角速度和加速度。相邻两时刻之间的时间间隔为Δt,智能移动放线机器人的运动学模型满足等式:

(1)

机器人实际位姿与参考位姿之间的误差为

(2)

跟踪误差为

(3)

式中,eR为距离误差;eψ为角度误差。

根据图1所示位置关系可以得到车辆的状态方程:

(4)

1.2 定位系统与观测方程

为满足机器人高精度放线的要求,将全站仪作为外部测量传感器。全站仪采集的数据为(r,φ)T,其中,r为距离,φ为全站仪在测量过程中的转动角度。全站仪具有极高的测量精度(100 m测量误差小于3 mm),但无法满足实时性要求(测量频率仅为5 Hz),且无法获得机器人的角度信息,因此综合使用里程计、微型惯性测量单元和全站仪,以提高系统测量频率,进而提高系统测量精度。图2为滤波补帧过程示意图。

图2 数据补帧处理示意图

系统的观测方程为

(5)

式中,(xm,ym)为全站仪在全局坐标系中的坐标;arctan2(*)为四象限反正切函数;εr、εφ分别为全站仪在测量过程中的距离测量噪声和角度测量噪声。

2 基于动态残差的ARUKF

智能移动放线机器人在工作过程中可能会出现强非线性的位姿变化,UKF通过无迹变换的方法解决卡尔曼滤波在推演过程中出现的非线性传递问题,对非线性运动的处理效果非常好。利用UKF需要提前预设系统噪声与观测噪声,但智能移动放线机器人的工作环境复杂、地面不平整,车体在运动过程中会持续抖动,很难预测多变的系统噪声或观测噪声的误差分布或误差类型,无法建立准确的函数模型和随机模型,因此,滤波过程需要减小更新参数的影响。

为解决该问题,引入抗差估计理论[14],根据系统观测量与预测量的动态残差来计算自适应加权因子,并利用加权因子对每个离散时刻的预测状态向量和预测误差协方差进行加权处理,从而使动态模型信息与测量值信息达到平衡,可实时修改状态方程以减小预设噪声特性与实际不符的影响,降低滤波过程中预测位姿信息数据发散的可能性,提高算法精度和鲁棒性。同时,利用最小策略采样减小系统的计算量,提高系统实时性。算法实现步骤如下:

(1)设定系统状态估计矩阵初值X0和误差协方差矩阵初值Σ0：

(6)

式中,Σx0、Σy0、Σθ0分别为系统X坐标、Y坐标和角度坐标的初始方差。

xt-1,i=

(7)

W=diag(wc,1,wc,2,…,wc,n)

wc,i=w0ρ2(C-1[1]n×n(CT)-1)ii=1,2,…,n

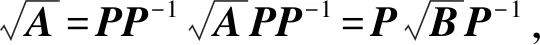
完成采样后,需对采集点进行变换,将t-1时刻的系统状态量xt-1,i在控制量ut的作用下转换为t时刻的系统状态量xt,i：

xt,i=g(ut,xt-1,i)

(8)

(9)

(10)

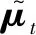
(11)

(12)

(13)

(14)

(15)

式中,St为观测量的协方差矩阵。

(5)计算动态残差

(16)

并设定自适应比例因子

(17)

(6)为减小不准确的预设噪声对系统的影响,利用抗差估计理论对状态量的估计值与估计协方差进行鲁棒性处理:

(18)

(19)

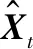
3 仿真与实地测试

3.1 仿真结果及分析

3.1.1仿真平台与参数设置

为验证ARUKF算法的精度和鲁棒性,借助MATLAB进行仿真测试,将UKF、基于Sage-Husa的改进无迹卡尔曼滤波(AUKF)和ARUKF在相同参数和控制量下进行对比实验。

仿真路径的第一段为直线,起点为(0,0),终点为(9 m,0);第二段为圆弧,起点为(9 m,0),终点为(9 m,3.82 m),半径为1.91m;第三段为直线,起点为(9 m,3.82 m),终点为(0,3.82 m)。运动过程中,不断对速度控制量U施加随机扰动来模拟地面不平整出现的车体抖动。系统参数设置如表1所示。

表1 仿真实验系统参数

3.1.2仿真测试结果与分析

如图3a所示,ARUKF最贴近真实值,AUKF次之,UKF偏差最大。图3b中,UKF误差最大、波动较大,AUKF误差较大、波动较小,ARUKF误差最小、波动最小。图3c中,AUKF误差最大、波动较大,UKF误差较大、波动较小,ARUKF误差最小、波动最小。图3表明在受到外部扰动影响时,相较于UKF和AUKF,ARUKF的距离误差和角度误差的波动更小,具有更好的鲁棒性。

(a)位置估算图

如表2所示,在相同的初始参数和控制量的作用下,ARUKF的距离误差均值为UKF的42%,角度估算误差均值为UKF的83%,ARUKF的距离误差均值为AUKF的50%,角度估算误差均值为AUKF的73%。这表明在受到外部扰动影响时,相较于UKF和AUKF,ARUKF的距离误差和角度误差更小,具有更高的精度。

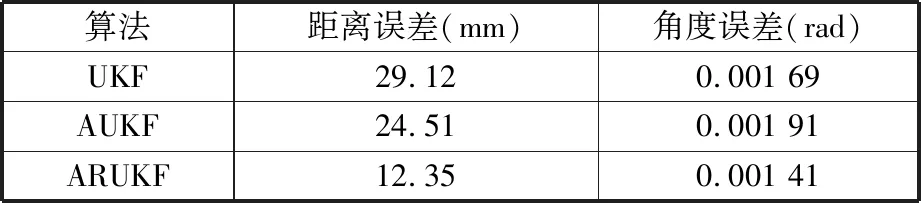
表2 仿真实验结果均方根误差

表3所示为ARUKF算法在直线运动和曲线运动时的均方根误差。ARUKF算法在直线运动与曲线运动下的距离误差和角度误差相近,都具有较高的精度和较好的鲁棒性。

表3 各运动状态误差对比图

3.2 实地测试

3.2.1系统组成与实验设置

为验证智能移动放线机器人的实际应用效果,在某施工现场进行实地测试。现场地面为未整平的水泥地面,存在大量不规则分布的凹陷和凸起障碍物。搭建的前驱式双轮差速运动底盘搭载有轮式里程计、微型惯性测量单元和测量棱镜,外置设备为全站仪天宝S5。主控制器为Beckhoff公司的工业PC,路径设置的预处理计算机通过有线与控制器进行数据交互。主控制器与驱动器通过CANopen总线进行控制。系统架构如图4所示。

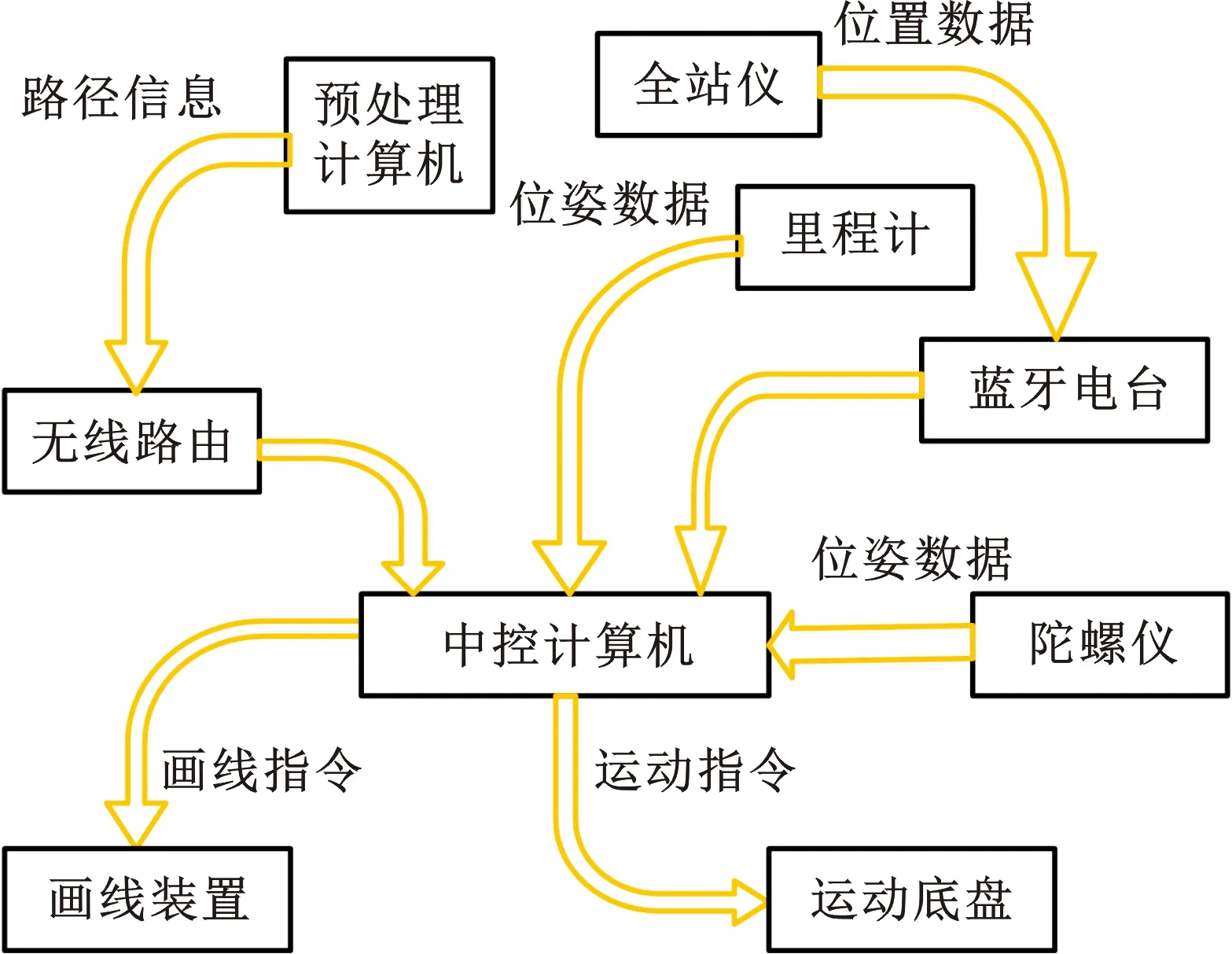
图4 系统结构示意图

实车测试平台如图5所示,移动机器人的轮间距为245 mm,行驶速度为0.2 m/s,采样周期为10 ms。

图5 实车测试平台

设定系统参数如下:

Σ0=diag(1,1,1,1)

Q=diag(0.001,0.001,0.001,0.001)

R=diag(0.0035,0.0036,0.0044,0.0045)

车体移动速度由里程计和微型惯性测量单元获取。实验过程中,根据实际工况完成一个完整U形运动,运动包含三种运动基本状态(直线、曲线和自旋)。通过对比实验来验证智能移动放线机器人系统的精度和稳定性,其中,直线段一起点为(2 m,0),终点为(4 m,0);曲线段起点为(4 m,0),终点为(4 m,3 m),半径为1.5 m;直线段二起点为(4 m,3 m),终点为(2 m,3 m);在点(2 m,3 m)处进行逆时针90°自旋。

实验1使用UKF算法进行定位,实验2使用ARUKF算法进行定位。两组实验均采用基于前馈运动学和带有干扰观测器的解耦动力学的混合控制算法[13]进行轨迹跟踪控制。两组实验的参数与控制率完全相同。

3.2.2测试结果与分析

实车测试结果如图6所示。图6a中,ARUKF算法的定位精度更高,智能移动放线机器人在直线段和曲线段的移动轨迹都更贴近目标轨迹。

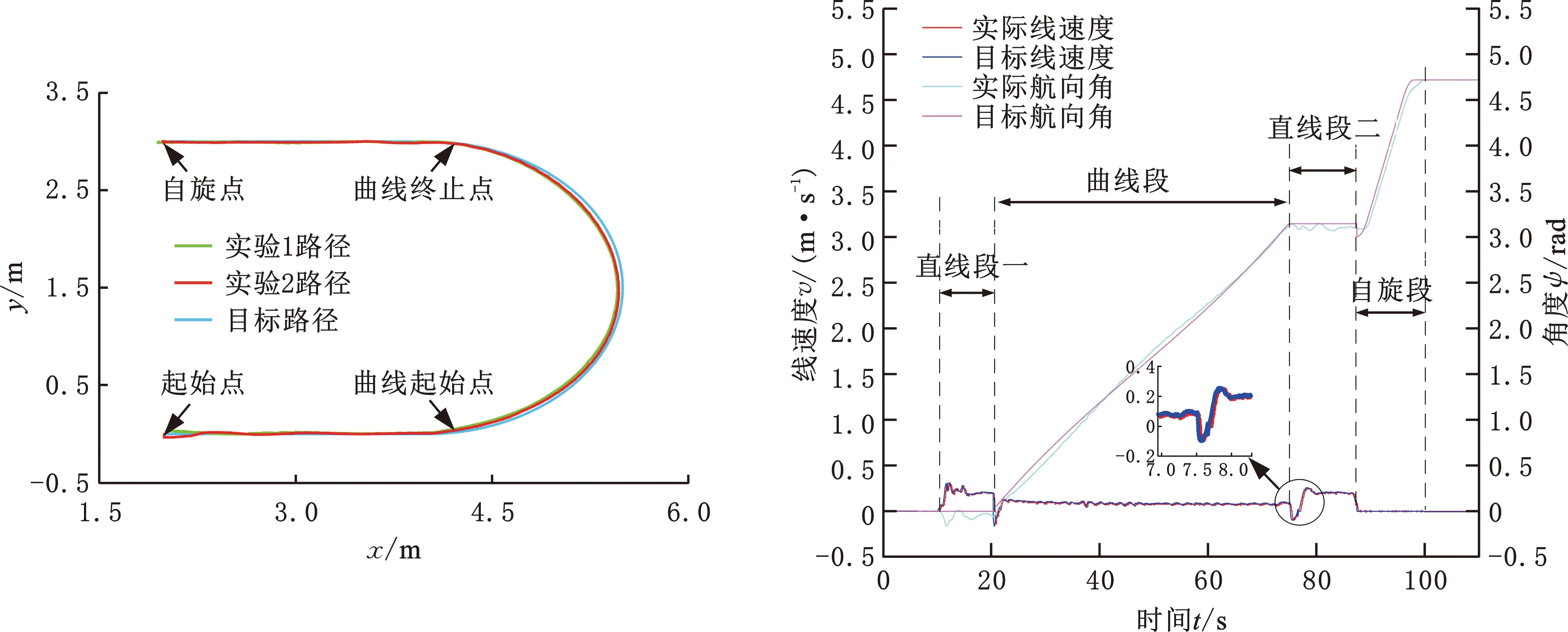
(a)路径跟踪示意图 (b)实验1的线速度和航向角示意图

图6b、图6c中,智能移动放线机器人由曲线段转到直线段二时,实验1的速度先跳至负值,然后缓慢增大,实验2并未出现此种情况。产生这种差异的原因是UKF算法的定位精度较差,在路径衔接处出现较大误差,智能移动机器人出现过冲,运动超出预设位置后需要调整位姿。ARUKF算法的精度更高,运动过程中的误差更小,速度更加平稳,车辆发生的抖动更小,系统更稳定。

如图6d所示,实验1的直线段和曲线段的误差都出现小范围的剧烈波动,实验2的波动更小、曲线更平滑。这是因为实际施工环境中的地面不平整,智能移动放线机器人在运动过程中出现车身抖动,而ARUKF具有更强的鲁棒性,因此其抗干扰能力更强、数据波动更小、曲线更平滑。实验1的自旋段距离误差一直在零点附近波动,实验2则不存在此情况,这是因为ARUKF根据动态残差实时调整了预测值和预测协方差,减少了系统噪声对定位结果的影响。

图6e为车体运动过程中的角度误差示意图,实验1的自旋段角度误差为0.037 rad,实验2的自旋段角度误差为0.017 rad。这是因为ARUKF使用的采样方法为最小采样方法,减小了系统运算量,提高了运算速度和系统实时性。

实验结果中,距离误差的均方根误差如表4所示,角度误差的均方根误差如表5所示。由于移动机器人的初始位姿会导致误差数据波动,因此误差数据取自系统稳定运行之后,以排除智能移动放线机器人初始位姿差异产生的影响。

表4 实车测试距离误差的均方根误差

表5 实车测试角度误差的均方根误差

如表4、表5所示,UKF算法的定位精度较低,定位过程中数据出现发散现象,鲁棒性不足,机器人出现过冲的问题,实验的平均距离误差为9 mm,最大距离误差为13.6 mm,平均角度误差为0.033 rad,最大角度误差为0.62 rad;机器人在不同运动状态时的定位精度波动大,曲线运动的误差远大于直线运动的误差。ARUKF算法的定位精度较高,系统运行稳定,实验的平均距离误差为2 mm,最大距离误差为2.9 mm,平均角度误差为0.015 rad,最大角度误差为0.36 rad;机器人在不同状态时的定位精度相近。

综上所述,自适应鲁棒无迹卡尔曼滤波算法具有高精度、强鲁棒性和高实时性的特点。虽然车体在运动过程中存在由地面不平整产生的抖动,但智能移动机器人可以迅速调整自身状态使自身状态收敛并保持稳定,这体现了ARUKF算法极高的定位精度与鲁棒性。实验过程中的平均距离误差小于3 mm,满足建筑施工要求,可以用于地面环境复杂、存在大量分布不规则凹陷和凸起障碍物的实际施工现场。

4 结论

本文结合抗差估计理论,提出了一种自适应鲁棒无迹卡尔曼滤波算法。该算法利用系统观测量与预测量之间的动态残差计算自适应加权因子,进而利用加权因子对每个离散时刻的预测状态向量和预测误差协方差进行加权处理,从而使动态模型信息与测量值信息达到平衡,可实时调整状态方程,减小外部干扰对系统预测值的影响,通过减小采样的运算量来提高系统运算的效率。仿真和施工现场测试结果表明,自适应鲁棒无迹卡尔曼滤波算法在系统存在不规则、不确定的扰动时能快速收敛,并获取精准位姿。相较于无迹卡尔曼滤波算法和基于Sage-Husa的改进无迹卡尔曼滤波算法,具有更高的精度、更强的鲁棒性和更高的实时性。