低寄生位移柔性平行微夹持器拓扑优化设计
2023-11-17汪启亮李永起魏健鸣徐美娟洪永烽
汪启亮 刘 通 李永起 魏健鸣 徐美娟 洪永烽
江西理工大学机电工程学院,赣州,341000
0 引言
与传统刚性机构相比,柔顺机构具有无摩擦、无运动副间隙、加工工序简单、免装配等优点[1-2],柔性微夹持器具有高精度、易操作、响应速度快等优点,因此广泛应用于微机电系统、机器人组装、精密加工、药物输送等多个领域[3-4]。微夹持器微装配和微操作中直接接触被夹持器物体[5],为使夹持器在夹持过程中不发生倾斜,需要夹持器能够平行夹持;为避免夹持器与被夹持物接触后不发生滑移现象,需要夹持器在夹持物体时具有较小的寄生位移。此外,柔性微夹持器一般选用压电陶瓷驱动器提供输入位移,压电陶瓷驱动器具有输出力大和精度高的优点,但是输出位移却很小,一般只有几十微米,因此,需要设计具有输入位移放大功能的低寄生位移柔性平行微夹持器。
为实现平行夹持,国内外学者基于传统机构设计了各种夹持器,如连杆机构[6]、三角放大机构[7]、平行四边形机构等[8-10]。杨群[5]基于柔顺机构方法设计了一种集成力和位移传感器的压电驱动平行微夹持器,能够实现位移放大和平行夹持,但未考虑寄生位移,且设计的机构较为复杂。GOLDFARB等[8]和NAH 等[9]基于杠杆机构和平行四边形机构设计出了具有位移放大效果的平行微夹持器,该夹持器结构简单但仍存在较大的寄生位移。XIAO等[11]设计了一种简单对称结构的新型夹持器并进行了优化设计,但是其同样只考虑了平行夹持而未考虑寄生位移。CHEN等[7]基于三角位移放大机构设计出了一种混合驱动微夹持器,其寄生位移降低到3.46%。LIANG等[12]将平行四边形机构集成到微夹持器中,设计出了一种三级位移放大的非对称平行夹持器,寄生位移为3.26%,存在的寄生位移仍会对夹持效果产生影响,以上柔性微夹持器多为研究人员根据传统机构基于经验进行设计,因此难以使夹持器的平行夹持、位移放大和低寄生位移等性能目标均得到优化,所以需要探索新的柔性微夹持器设计方法。
柔顺机构拓扑优化方法无需从一个已知的刚性机构出发[10],只需给定设计域和输入输出位置[13-14],通过添加不同目标和约束使机构的一种或多种性能得到优化,提高了柔顺机构设计的效率和灵活性,因此拓扑优化方法可用于柔性微夹持器设计。CHI等[15]以柔度为目标进行柔性微夹持器拓扑优化设计,结合人工识别使得夹持器具有近似平行夹持功能,拓扑优化模型中并未对旋转和寄生位移进行抑制。LIANG等[16]采用两步非线性多约束拓扑优化方法设计了一种单边平行微夹持器,但是该拓扑优化微夹持器仍存在一定的寄生位移。因此,需要进一步研究低寄生位移柔性平行微夹持器拓扑优化设计方法以提高其综合性能。
本文结合多目标拓扑优化方法和分层序列法设计低寄生位移的柔性平行微夹持器,采用改进的固体各向同性材料惩罚(solid isotropic material penalty,SIMP)模型,以输出位移、机构刚度、寄生位移、旋转角度的线性加权组合作为多目标拓扑优化的目标函数,以优化准则法对模型进行求解,通过迭代优化寻找新型柔性平行微夹持器。
1 优化模型的建立
1.1 基于SIMP材料插值模型的拓扑描述
拓扑优化是为了在给定设计域内寻找材料最优分布,最终使结构在满足一定约束条件下,某项或多项性能指标达到最优,拓扑优化问题的一般表达式为
(1)
式中,w为设计变量;N为设计变量个数;f为目标函数;gj为约束函数;m为约束函数个数;gv为体积约束;V0为初始设计域总体积;Vf为体积比。
在变密度法中,为了使设计变量wi在0和1之间连续分布,需要对材料分布函数进行插值。目前最常用的密度插值模型为改进的SIMP模型,将设计域离散为N个有限单元,每个单元的密度对应一个设计变量,通过在离散模型中引入连续设计变量w(0≤w≤1)和惩罚因子p(p>1),使得优化前和优化后的弹性模量有如下关系式:
(2)
0≤w≤1
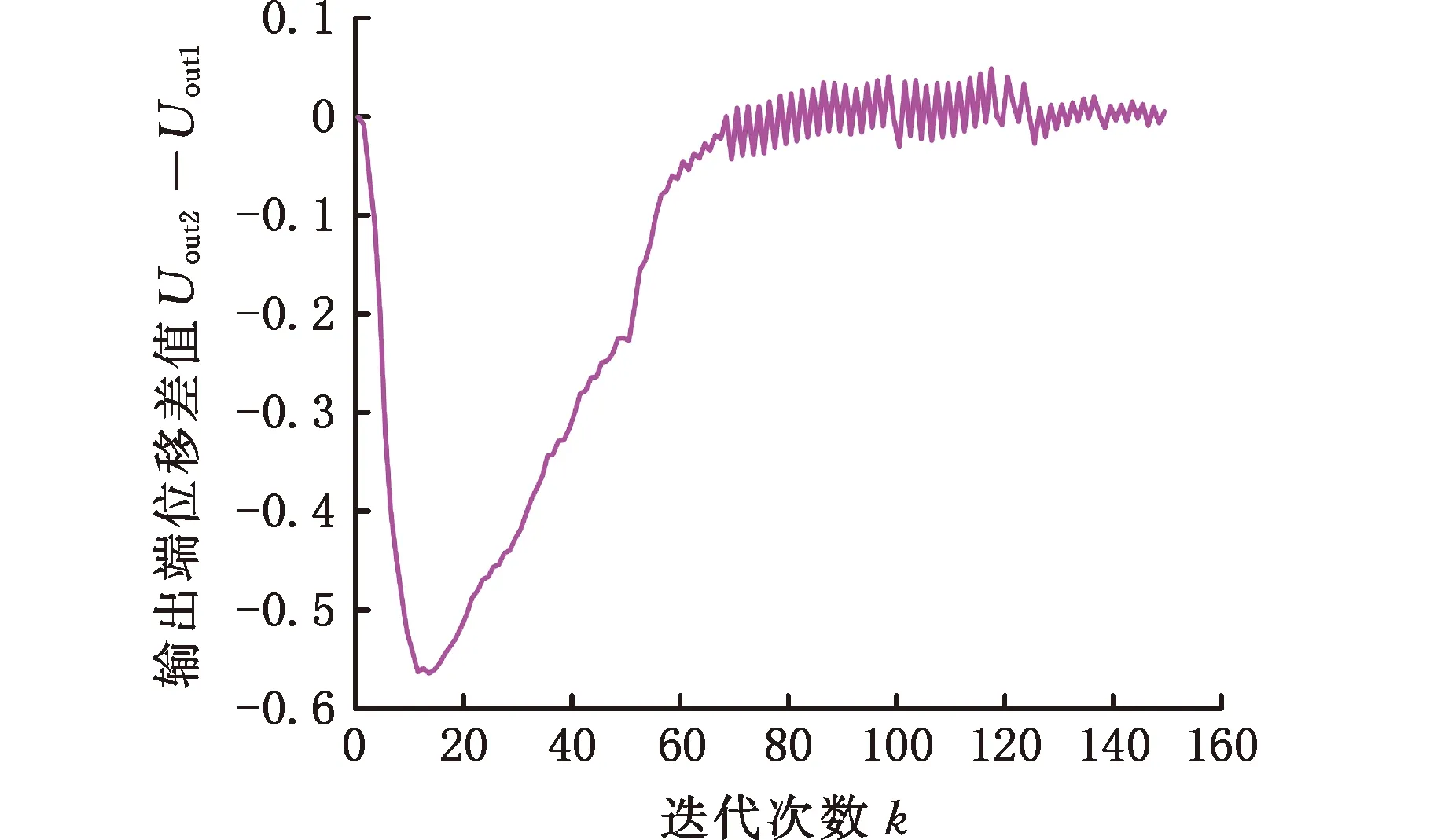
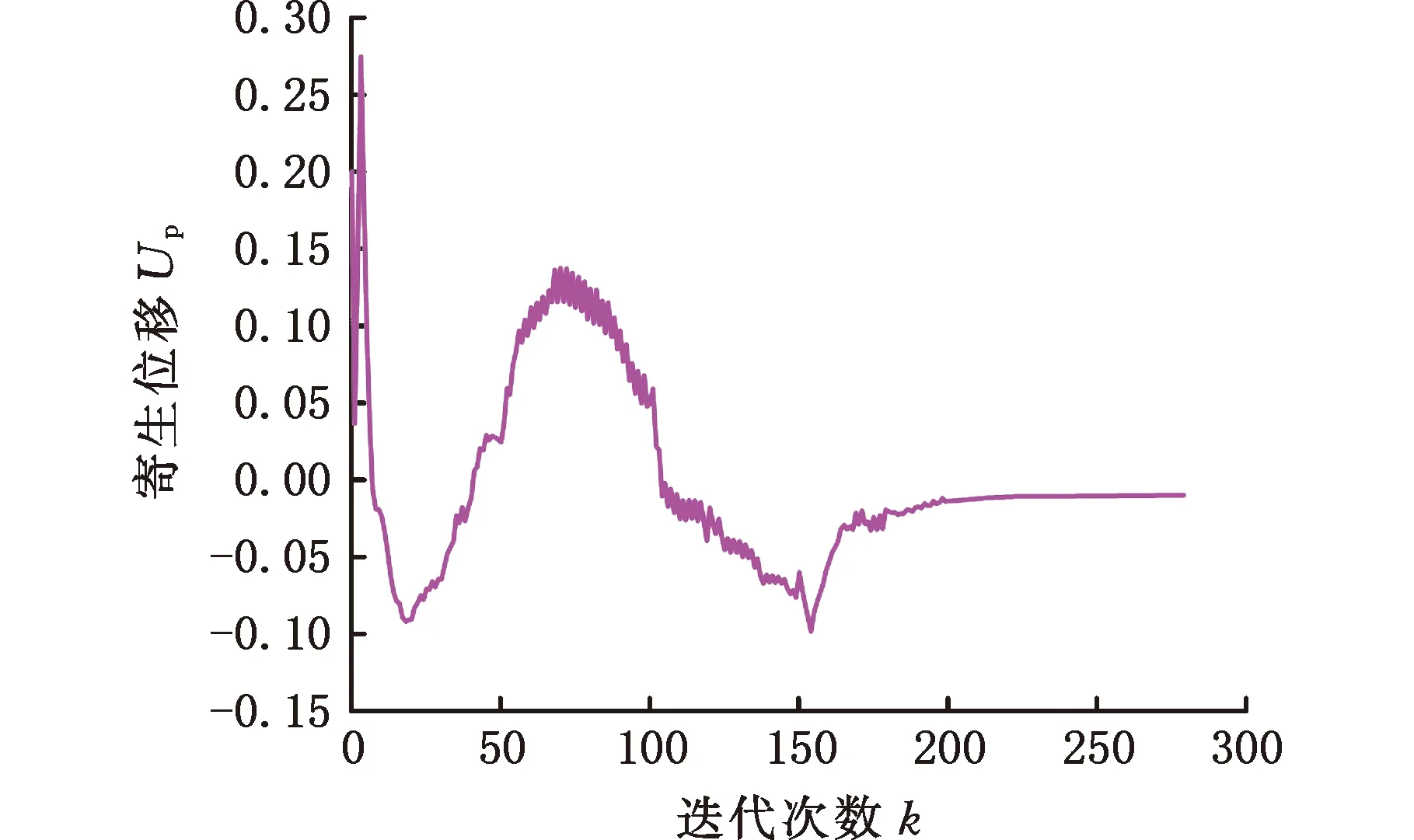
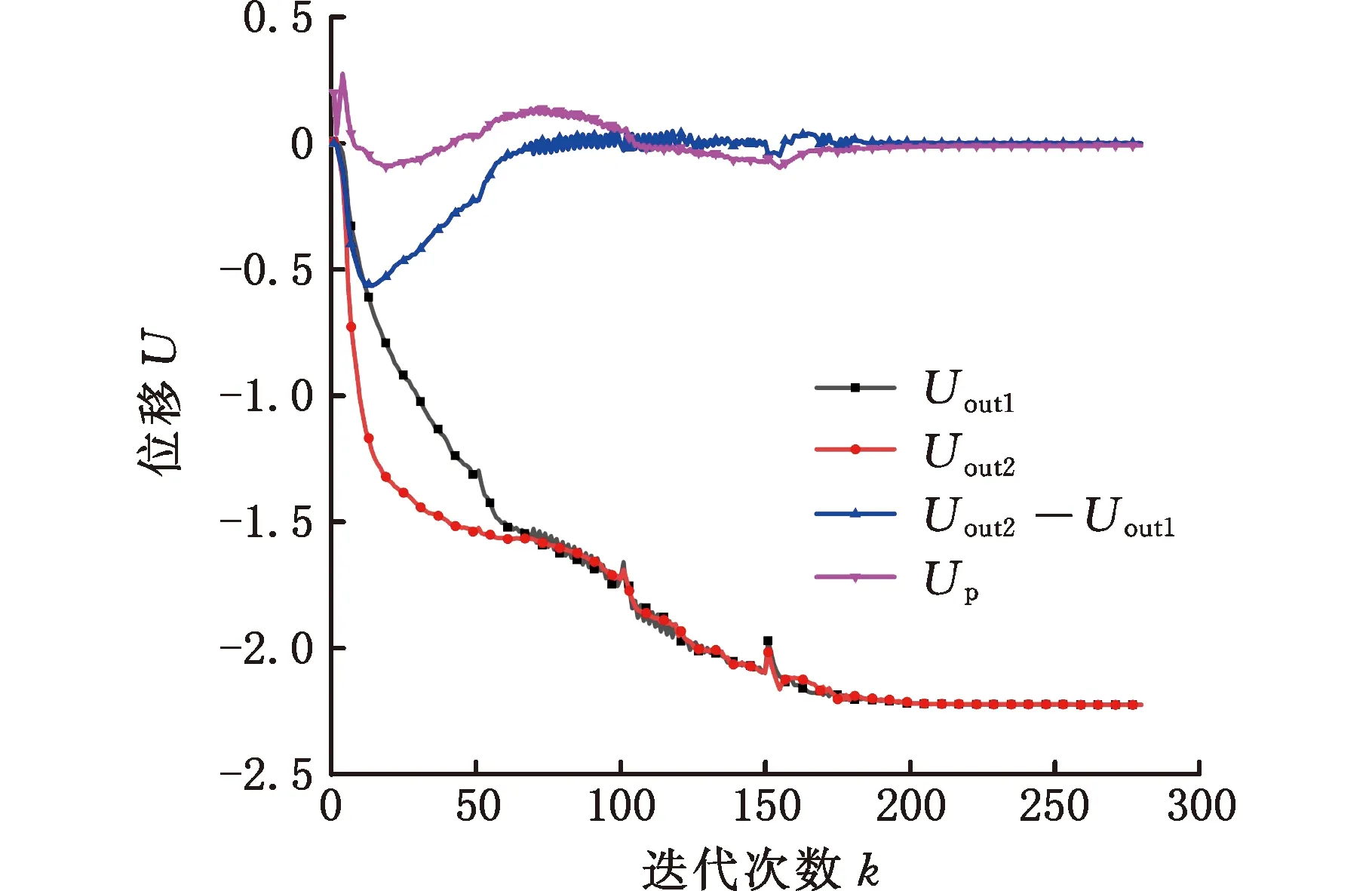
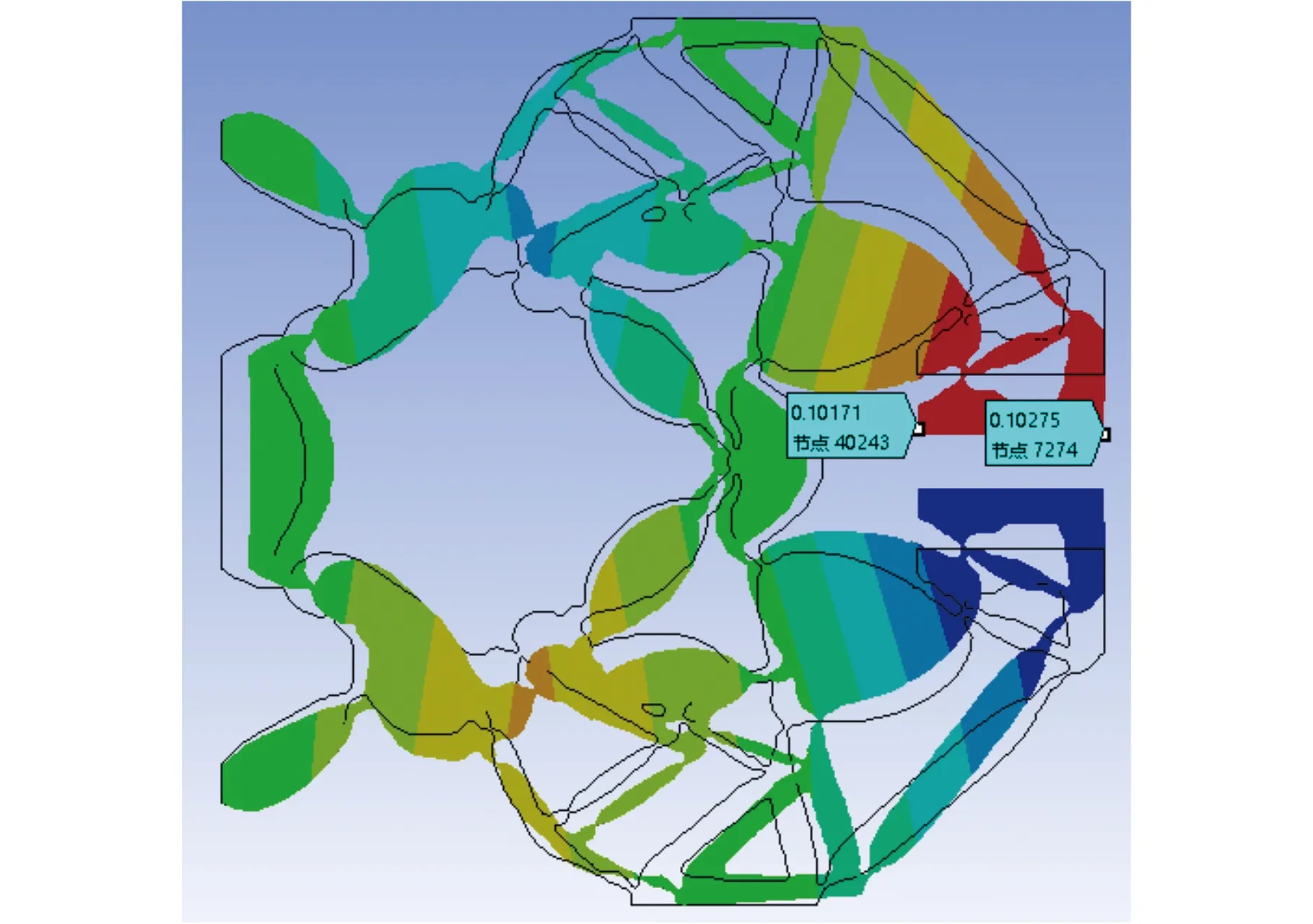
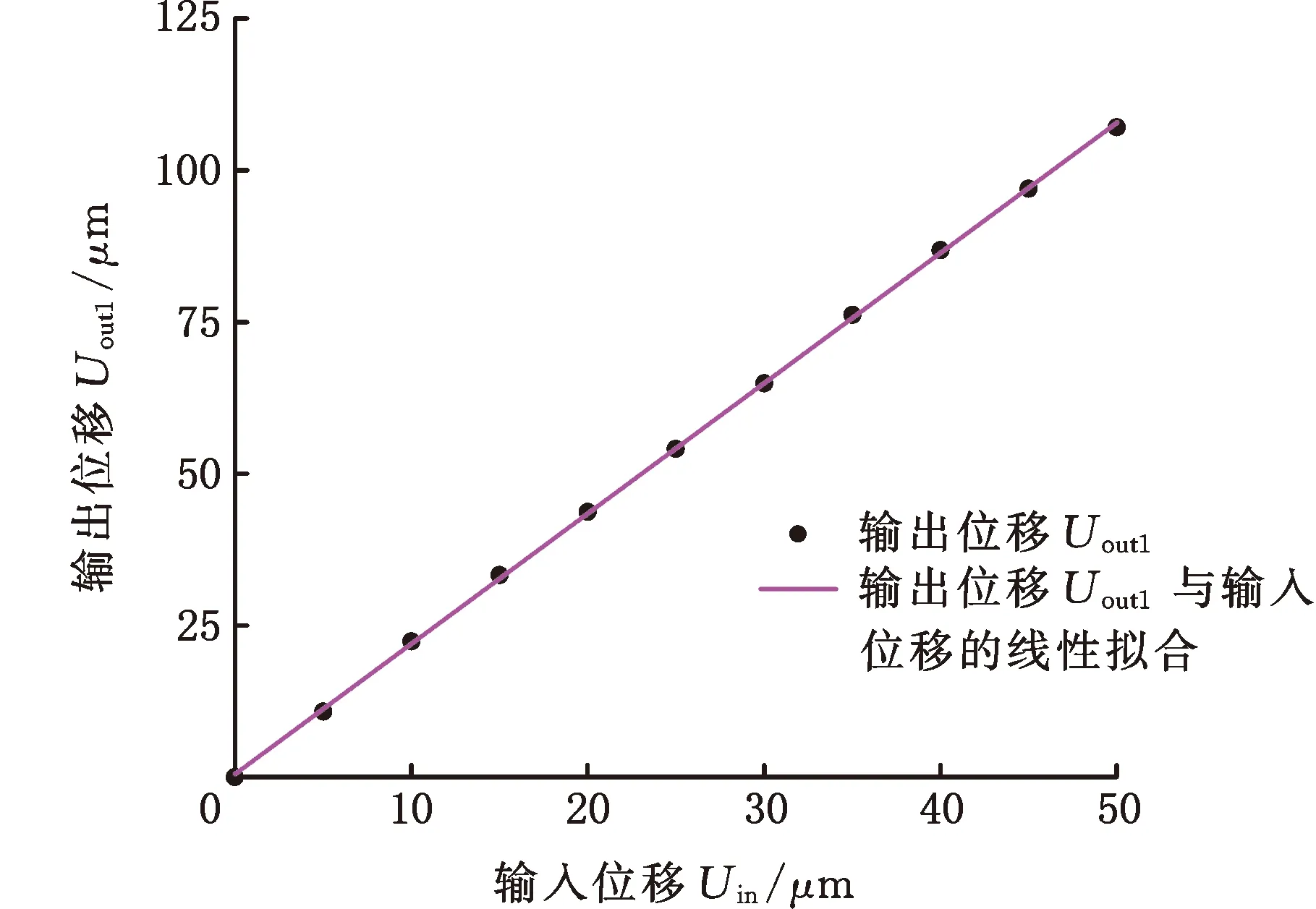
式中,E0、Ei分别为优化前和优化后的弹性模量;Emin(0 设计变量wi=1表示单元充满材料,设计变量wi=0表示单元没有材料。式(2)通过引入Emin避免单元密度为0,能有效避免刚度矩阵奇异。 为得到具有位移放大功能和低寄生位移的平行微夹持器,采用拓扑优化方法寻找满足条件的新型微夹持器。设计的微夹持器为对称机构,因此设计域可以取对称机构的一半,设计域如图1所示。黑色区域为夹持部位,图中A点为输入端,B点和C点为两个输出端,B、C两点y方向的输出位移可用来评估机构旋转程度,C点x方向位移用来评估相对寄生位移大小。Fout1和Fout2为输出端的虚拟载荷,Uout1和Uout2分别为末端执行器输出端B点和C点沿y方向的输出位移,Up为输出端C点沿x方向的位移,Kin用来模拟压电陶瓷与微夹持器间的输入刚度。 图1 微夹持器的设计域 为实现平行夹持,需对旋转角度和寄生位移进行抑制,其中旋转的抑制是通过使B、C两点y方向位移差值最小化来实现,而寄生位移的抑制通过C点x方向的位移实现,基于此,可将旋转角度和寄生位移的抑制作为目标引入目标函数。平行微夹持器选用压电陶瓷驱动器作为位移输入源,由于它能提供的行程有限,因此设计的柔性平行微夹持器应具有位移放大功能;另一方面,拓扑优化过程中常因为刚度不足而导致优化结果出现断裂和虚铰链的现象,通过引入刚度目标函数可以有效解决这一问题。 综上,低寄生位移柔性平行微夹持器的拓扑优化为多目标优化问题,本文通过线性加权法将多目标拓扑优化问题转化为单目标拓扑优化问题,并根据目标重要程度设置权重因子。对于难以同时达到最优的目标,则通过分层序列法将多目标拓扑优化分为两步进行优化,每步主要的优化目标不同,具有不同的线性加权因子和不同的目标函数。 第一步:为了实现位移放大和平行夹持,以输出端位移和旋转角度作为目标函数进行优化,目标函数为 minf1(w)=a1M1+a2M2+a3R+a5S1+a6S2 (3) (4) (5) 其中,R为抑制旋转角度的目标函数,通过改变迭代方向实现抑制效果。微夹持器的位移可由机构的互应变能表征,即M1和M2;微夹持器的刚度可由机构的应变能表征,即S1和S2;K为全局刚度矩阵,其值与单元弹性模量E(wi)有关;k0为单元刚度矩阵;wi为单元的相对密度,即平行微夹持器的设计变量;Uin为输入力Fin作用下的全局位移矢量;Uout1和Uout2分别为输出虚拟载荷力Fout1和Fout2作用下的全局位移矢量;a1,a2,…,a6为权重因子。 第二步:为降低平行微夹持器夹持时的滑移现象,需要抑制输出端的寄生位移,因此,在通过第一步优化使得微夹持器旋转角度达到足够小后,对其寄生位移进行抑制,目标函数表示为 minf2(w)=a1M1+a2M2+a3R+a4Q+a5S1+a6S2 (6) (7) 其中,Up为水平方向输出虚拟载荷力Fp作用下的全局位移矢量;Q为抑制寄生位移的目标函数,在迭代优化过程中迭代方向随Up正负号的变化而改变,进而实现寄生位移的抑制。 综上,第一步通过迭代优化增大输出位移放大比,同时通过抑制微夹持器的旋转角度以实现平行夹持,拓扑优化问题可以表示为 (8) 其中,Vi为第i个单元的体积。 第二步通过迭代优化使平行微夹持器的寄生位移降低到收敛值,在此阶段,机构的放大比会进一步增大,拓扑优化问题可以表示为 (9) 求解连续体拓扑优化问题常用的方法有优化准则(OC)法[17]和移动渐进(MMA)法[18]。OC法主要用于求解单约束拓扑优化问题,而MMA法可用于求解多约束拓扑优化问题。在单约束拓扑优化中,OC法具有收敛速度快和求解结果稳定的优点[19],故本文选用OC法进行求解,单元密度的更新方案如下: (10) 其中,m为最大移动步长;μ为阻尼系数,用于保证迭代优化过程中数值计算的稳定性,本文中取0.5[20]。 拓扑优化的优化准则Bi可由下式给出: (11) 其中,λ为拉格朗日乘子,可以通过二分法求出。 求解优化问题时通常需要推导目标函数f(w)和约束函数g(w)对设计变量的敏度信息,可以采用伴随法进行敏度分析。因为拓扑优化分两步进行,存在不同的目标函数,所以分别计算其敏度。 第一步的敏度计算:目标函数f1(w)关于设计变量的敏度可以表示为 (12) (13) 第二步的敏度计算:目标函数f2(w)关于设计变量的敏度可以表示为 (14) (15) 体积约束函数g(w)的敏度为 (16) 其中,uin为输入力Fin作用下的单元位移矢量;uout1、uout2分别为虚拟载荷力Fout1和Fout2单独作用下的单元位移矢量;up为虚拟载荷力Fp作用下的单元位移矢量。 图1所示为柔性平行微夹持器的设计域,将其划分为100×200的四节点矩形单元。结构尺寸和材料均采用量纲一的量。因为设计的平行微夹持器结构对称,上下两部分受力情况相同,因此,本文以微夹持器的上半部分作为设计域进行拓扑优化。左上角为微夹持器的固定端,限制AD线段所在单元的y方向位移。设置左下角A节点为微夹持器的输入端,输入方向为x方向,将设计域右端B、C两点定义为微夹持器的输出端,输出方向垂直于输入方向。设置输入端输入载荷Fin=1,虚拟输入弹簧刚度大小Kin=1,输出端虚拟输出负载Fout1=1,Fout2=1,Fp=1。弹性模量E0=1,弹性模量下限Emin=1×10-6,泊松比υ=0.3,材料惩罚因子p=3,体积约束比为35%。 根据式(8)中的平行微夹持器理论模型,利用MATLAB编程并求解该拓扑优化问题,得到第一步拓扑优化优化结果如图2所示,然后再根据式(9)中的平行微夹持器理论模型,利用MATLAB进一步优化得到平行微夹持器的最终构型如图3所示,其中第一步和第二步的权重因子如表1所示。 表1 第一、二步迭代的权重因子 图2 第一步拓扑优化结果 图3 第二步拓扑优化结果 在本设计中,末端执行器B点和C点沿y方向的位移差值(Uout2-Uout1)可以反映机构旋转角度的大小,图4所示为第一步迭代过程中旋转角度迭代过程。随着迭代次数的增加,微夹持器的旋转角度逐渐减小,在迭代次数k为150时达到收敛条件: 图4 旋转角度迭代过程 (17) 图5所示为寄生位移Up迭代过程。在第二步中将寄生位移引入目标函数,机构的寄生位移持续减小,在迭代次数k为280时满足收敛条件则迭代结束: 图5 寄生位移迭代过程 (18) 其中,ε为相对寄生位移。 图6所示为柔性平行微夹持器末端输出位移Uout1、Uout2、旋转角度Uout2-Uout1、寄生位移Up的优化迭代过程,图中Uout1和Uout2分别为A点单位输入位移作用下B、C两点y方向的输出位移。由该图可以看出,在第一步优化迭代中,平行微夹持器的输出位移随迭代次数的增加而不断增大,而旋转角度不断减小,且在第一步迭代结束时满足收敛条件。在第二步优化迭代中,机构的输出位移继续增大,在210步左右达到极限值2.224,同时因为引入了寄生位移目标函数,机构的寄生位移和旋转角度进一步减小,最终在迭代到280步时达到收敛条件。拓扑优化柔性微夹持器理论的单位寄生旋转为9.8×10-9mrad/μm,相对寄生位移为0.44%。 图6 微夹持器拓扑优化迭代过程 在柔性平行微夹持器的拓扑优化设计时,不同的刚度权重因子会对拓扑优化结果产生影响。为了研究刚度权重因子对拓扑优化结果的影响程度,在其他参数不变的情况下,选取不同的刚度权重因子进行拓扑优化,得到对应于不同权重因子的拓扑优化微夹持器,相应的放大比、两端位移差值(Uout2-Uout1)、相对寄生位移如表2所示。由表中数据可以看出,平行微夹持器的放大比Ra随着刚度权重因子的增大而逐渐减小,这是因为刚度权重因子影响了拓扑优化的迭代方向。由表2可知,刚度权重因子较小时,机构的放大比会更大,但同时机构的旋转角度和相对寄生位移也会增大。不同刚度权重因子对应的最终拓扑图见图7,随着刚度权重因子的增大,机构铰链分布的区域更加分散,拓扑图形边缘轮廓也更易提取。因此需要选择合适的刚度权重子来寻求多目标拓扑优化的最优解。 表2 不同刚度权重因子下的微夹持器性能 (a)a5,1=0.0001 (b) a5,2=0.0002 为了验证方法的有效性,不考虑旋转角度和寄生位移的抑制,在相同的设计域和相同的输入输出条件下拓扑优化得到普通微夹持器,拓扑优化结果如图8所示,采用ANSYS Workbench对两种微夹持器进行有限元仿真和对比。 图8 普通微夹持器拓扑优化结果 提取图3和图8的拓扑图边缘,利用UG软件进行三维建模。使用ANSYS Workbench进行仿真分析。材料采用7075铝合金,弹性模量为71 GPa,泊松比为0.3,设置最小单元参数为0.5 mm进行网格划分。给定输入位移为50 μm,两种微夹持器的仿真结果如图9所示,旋转角度、寄生位移、相对寄生位移等性能对比如表3所示。 表3 两种微夹持器的性能仿真对比 (a)新型平行微夹持器y方向输出位移 由图9和表3可知,当输入位移为50 μm时,未抑制旋转角度和寄生位移的普通微夹持器末端执行器两端x方向的位移差值为71.73 μm,旋转角度可计算为3.132 mrad,单位寄生旋转为0.0238 mrad/μm,寄生位移为65.32 μm,相对寄生位移为49.6%。在拓扑优化中添加对寄生位移和旋转角度的抑制后,得到的新型平行微夹持器末端执行器两端x方向位移差值为1.04 μm,旋转角度可计算为0.038 mrad,单位寄生旋转为0.000 373 6 mrad/μm,寄生位移为0.595 91 μm,相对寄生位移为0.58%。对比上述两种微夹持器的旋转角度和寄生位移可知,通过在算法中抑制旋转角度和寄生位移,微夹持器能实现低寄生位移的平行夹持,进一步验证了平行微夹持器设计算法的有效性。 为了验证拓扑优化柔性微夹持器的低寄生位移和平行夹持性能,采用尼龙材料3D打印出该平行微夹持器,搭建实验平台测试其性能,如图10所示。微夹持器采用压电陶瓷驱动器(PSt150/7/80VS12, Core Tomorrow)进行位移输入,夹持末端的输出位移由激光位移传感器(LK-H025,Keyence)测量,微夹持器的寄生位移则由精度更高的激光位移传感器(LK-H008,Keyence)测量。 图10 平行微夹持器实验装置 在给定0~50 μm的输入位移下,测量微夹持器末端两端点y方向的输出位移和x方向的寄生位移,并计算出微夹持器的旋转角度,测量数据如图11所示。当输入位移为50 μm时,两端输出位移差值为3.9 μm,寄生位移为0.725 μm,相对寄生位移为0.7%,旋转角度为0.142 857 mrad,单位寄生旋转为0.001 384 27 mrad/μm。机构的输出位移与输入位移、寄生位移与输入位移、机构的旋转角度与输入位移均呈线性变化。相对寄生位移的仿真值与实验值相差0.12%,单位寄生旋转的仿真值与实验值相差0.001 01 mrad/μm。造成以上误差的原因可能来自于加工误差、机械振动、测量点漂移等。即使存在一定误差,相对寄生位移的仿真值与实验值均小于1%,单位寄生旋转的仿真值与实验值都小于0.002 mrad/μm。仿真结果和实验结果均表明所设计的新型平行微夹持器不但能够实现平行夹持,而且具有较小的寄生位移,进一步验证了设计方法的有效性。 (a)B点y方向输出端位移随输入位移的变化 本文提出了低寄生位移柔性平行微夹持器的拓扑优化设计方法,以输出位移与输入位移比最大、旋转角度最小、寄生位移最小和末端刚度为目标函数,利用线性加权法将多目标问题转化为单目标问题,建立了平行微夹持器的拓扑优化模型,使用分层序列法根据目标函数重要程度将优化过程分为两步进行,分别详细推导了敏度信息。采用优化准则法对优化问题计算求解,用数值算例验证了所提出方法的有效性。探究了刚度权重因子对最终拓扑优化结果的影响规律,分别对低寄生位移平行微夹持器和普通微夹持器进行仿真分析和对比,最后加工出平行微夹持器,测得其相对寄生位移低至0.7%,单位寄生旋转为0.001 384 27 mrad/μm。所设计的微夹持器能够实现低寄生位移和平行夹持,验证了本文方法的有效性。本文为低寄生位移柔性平行微夹持器设计提供了一种新思路。1.2 平行微夹持器设计问题的描述
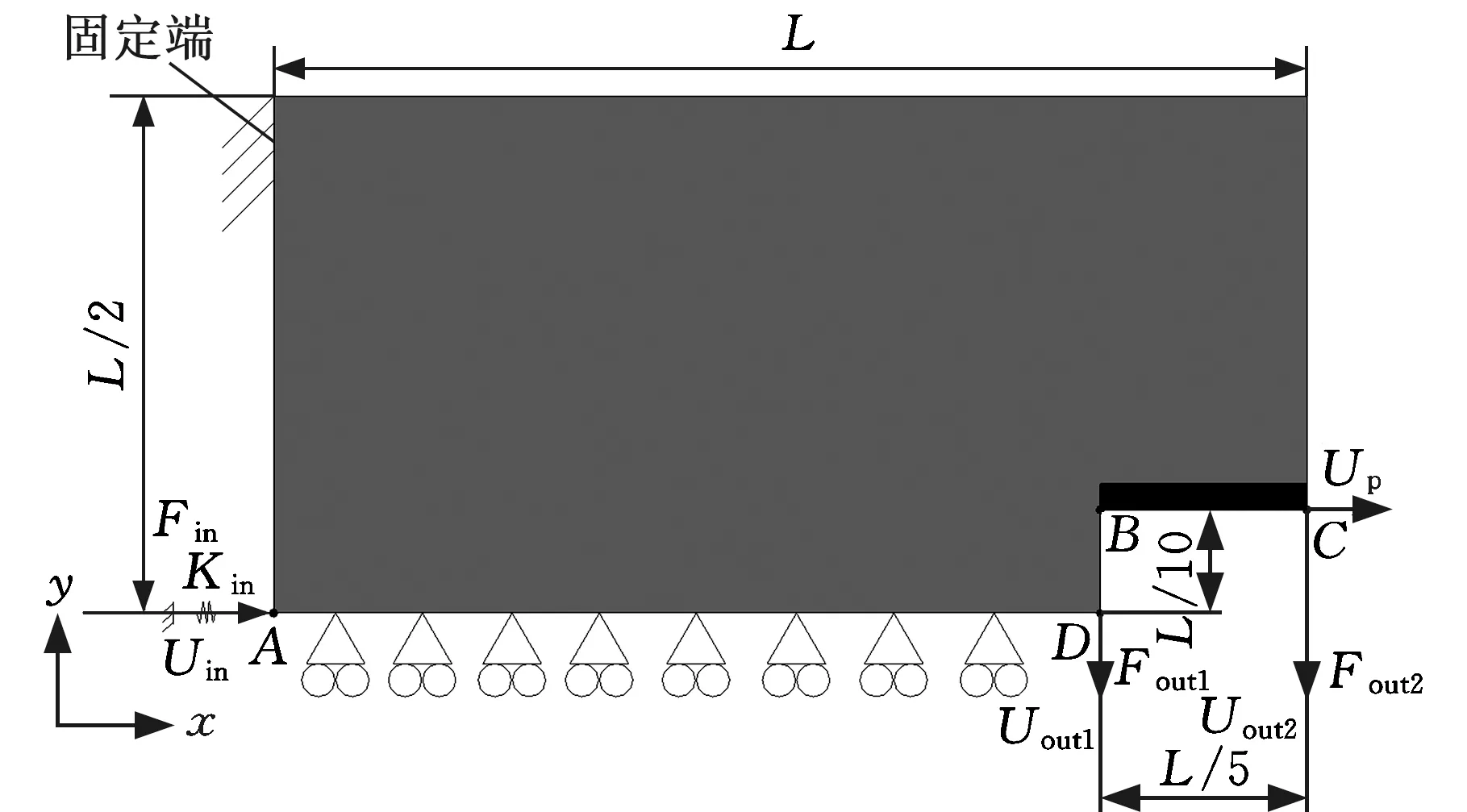
2 敏度分析
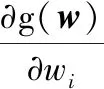
3 数值算例





4 仿真对比与实验研究
4.1 微夹持器仿真分析与对比

4.2 实验验证

5 结论
