石墨烯/h-BN 面内异质结构热输运的分子动力学研究
2023-11-16朱俊杰王继芬
朱俊杰, 王继芬
(上海第二工业大学a. 资源与环境工程学院; b. 上海先进热功能材料工程技术研究中心,上海 201209)
0 引言
近年来,伴随着航天、机械、医药等行业的尖端科技需求不断增加,半导体产业发展日新月异,电子元件的理论研究、构型设计和工艺制备在不断地创新和完善中蓬勃发展。微纳米尺寸下的电子元件作为半导体产业中至关重要的一环,其性能很大程度上依赖于自身的架构、材料的特性以及使用环境的温度、湿度等因素。因此,研究高导热性能的散热材料来稳定微纳米尺寸电子元件的性能或是延长使用寿命是目前热门的科研方向。石墨烯是依靠sp2杂化相连接的碳原子堆积形成紧密的二维蜂窝状结构, 作为一种新兴材料在导热、导电、光学、力学等方面都具有优异的性能。然而石墨烯零带隙的特点阻碍了它在半导体领域的开发。为此, 研究人员采用将石墨烯功能化[1], 掺杂[2], 或与其他二维材料构造异质结构[3]等方法来改进石墨烯。h-BN 作为一种新型二维材料,具有与石墨烯相近的二维结构与晶格常数, 光、电等性质也相似[4-5], 有着“白色石墨烯” 的美誉, 其带隙值为5.9 eV[6]。这2 种二维材料所形成的异质结构具有特殊的电学性能和热学特性,室温下使用拉曼法测量的石墨烯具有2 000~5 000 W/(m·K)[7]的高热导率, 而h-BN 的热导率值范围也达到了1 700~2 000 W/(m·K)[8],在新型二维电子和光电子器件中有着广阔的应用前景。
目前, 石墨烯与h-BN 异质结构的相关研究十分广泛。2010 年,Ci 等[9]首次通过热催化化学气相沉淀法(chemical vapour deposition,CVD)在铜箔上成功制备石墨烯/h-BN 面内异质结构, 他们以单质铜作为基底,选用甲烷(CH4)作为石墨烯前体,选择氨硼烷(NH3BH3)用作h-BN 的前体进行制备,并测量出该异质结构的带隙为18 meV。Karak 等[10]用拉曼光谱法测量了SiO2/Si 衬底的石墨烯、h-BN 及2 种材料的范德华异质结构的面内热导率与层间热导, 他们发现用h-BN 对石墨烯进行封装可以有效提升其在SiO2/Si 衬底上的导热性能。当以SiO2/Si为衬底时, 上下两层h-BN 封装石墨烯的层间热导与面内热导率分别为105 和850 W/(m·K),而石墨烯的层间热导与面内热导率经测量分别为1.15 和600 W/(m·K),这证明h-BN 封装的石墨烯的散热性能更佳。在模拟计算中, 目前对石墨烯/h-BN 异质结构的尺寸、界面缺陷等要素对界面热导的影响均有所研究。Wu 等[11]基于GPU 架构进行GPUMD 模拟,研究了石墨烯和h-BN 等其他二维材料形成的层间范德华异质结构。结果显示,石墨烯/h-BN 范德华异质结构的热导率为300 MW/(m2·K),显著高于石墨烯与其他材料(例如MoS2、Cu、SiO2等)所形成的层间异质结构。Liu 等[12]使用非平衡分子动力学模拟探索了界面形貌优化对界面热导的影响,他们发现具有锯齿形的石墨烯/h-BN 面内异质结构的界面热导随着排列成锯齿状的原子行数增加而增加,扶手型界面形貌则具有相反的特性。考虑到在实际制备中,石墨烯、h-BN 或其他二维材料难免地会出现单空位缺陷(single vacancy, SV)[13-14]、双空位缺陷(double vacancy,DV)[13]和Stone-Wales(SW)[15-17]缺陷等情况, 在模拟实验中也会对此进行重点研究。Zhang 等[18]研究了石墨烯/h-BN 平面异质结构中石墨烯一侧存在单空位缺陷和585、F5F7 两种构型的双空位缺陷时对于界面热导的影响。结果表明,在相同数量下,双空位缺陷相较于单空位缺陷会引发更强烈的声子散射与更低的界面热导,这是由于前者具有更宽的横截面,并会引起更大的局部褶皱等原因。但是,关于石墨烯/h-BN 近界面出现单空位缺陷或其他缺陷类型时对于界面热导的影响研究仍需要深入探讨。
因此, 本文研究采用非平衡分子动力学模拟(non-equilibrium molecular dynamics, NEMD), 研究单空位缺陷和SW 缺陷在石墨烯/h-BN 异质结构在界面与近界面处不同位置的情况下,对界面热导的影响。此外,研究了界面处存在单空位缺陷时,温度变化对于界面热导的影响。即针对缺陷类型、位置、浓度对二维面内异质结构热输运特性的影响,并综合环境温度的变化,深入探讨了材料的热传导机制,为开发更高效、可控的热导材料提供理论指导。
1 实验方案
1.1 模型构建
石墨烯晶格常数为0.248 nm(2.48 ˚A)[19], h-BN晶格常数为0.250 nm (2.50 ˚A)[20], 晶胞高度取两者均值0.335 nm (3.35 ˚A)[12], 构建120×24×1 单位的超晶胞纳米带,长度为51.62 nm,宽度为5.97 nm,体系中共包含11 520 个原子。两侧边界至各自临近的左、右1/4 带之间的材料设置为h-BN,两根1/4 带之间的材料为石墨烯,由前人的研究结果可知[21], 锯齿形异质结构相较于扶手型异质结构更容易在制备中生成,因此异质结构界面的构型选用锯齿形界面,模型如图1 所示。
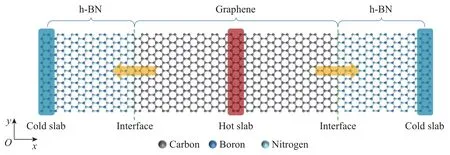
图1 石墨烯/h-BN 异质结构的计算模型Fig.1 Computational model of the graphene/h-BN heterostructure
单空位缺陷的构建,将CB 与CN 界面处B、N原子的单空位缺陷分别命名为CB-BV1 与CN-NV1,在h-BN 一侧近界面选取3 个位置, 按照移除的原子分别命名为CB-NV2、CN-BV2、CB-BV3、CNNV3、CB-NV4 和CN-BV4,如图2 所示。单空位缺陷随机分布在各位置上,缺陷浓度的定义为缺失的原子数与总原子数一半的百分比比值,浓度样本选择0%~0.06%,每0.02%选取一个样本。

图2 2 种界面中不同位置的单空位缺陷Fig.2 Single vacancy defects in different locations in both interfaces
SW 缺陷是由C—C 或者C—N 等共价键旋转90°所形成的拓扑结构缺陷,其结构如图3 所示。SW缺陷在界面处根据共价键的不同分别命名为CBCBW1、CN-CNW1、CB-CCW1 和CN-CCW1,近界面处则命名为CB-BNW2、CN-BNW2、CB-CCW2 和CN-CCW2。SW 缺陷浓度的定义参照单空位缺陷,为受扭转的原子数与总原子数一半的百分比比值,浓度样本选择0%~0.1%,每0.02%选取一个样本。

图3 2 种界面中不同位置的SW 缺陷Fig.3 SW defects in different locations in both interfaces
1.2 分子动力学模拟
研究采用非平衡分子动力学方法计算石墨烯/h-BN 面内异质结构的界面热导(interface thermal conductance, ITC)。为避免结构周期性的作用影响实验结果,在3 个方向上均选用了周期性边界条件,这可以有效降低边界声子散射等因素对于实验结果的影响,使计算结果更加可靠[22]。在垂直于面内的方向上设置了4 nm(40 ˚A)的真空层以防止周期性的层间作用对实验结果产生影响。采用Lindsay[23]所优化的Tersoff 势来描述B、N、C 原子之间的相互作用,这种势函数在石墨烯氮化硼体系的模拟实验中的准确性已得到广泛的认可与应用[15,24-25]。首先采用共轭梯度法(conjugate gradient, CG) 将体系进行能量最小化, 使体系逐渐稳定, 然后在正则系综(canonical ensemble,NVT)中驰豫400 ps,温度为300 K, 时间步长为0.5 fs; 然后将系综切换为微正则系综(microcanonical ensemble,NVE),对体系采用Langevin 热浴法进行局部热浴,热源温度设定为330 K,热汇温度设定为270 K,每隔100 ps 输出一次结果,热浴5 ns 后材料各部分温度分布逐渐稳定,统计热通量(J),温度梯度和热流梯度如图4、5 所示。进而求得传热速率Q= dJ/dt,t为热浴时间。最后计算界面热导ITC =Q/(A·ΔT)。其中:A代表异质结构界面的截面面积;ΔT代表界面两侧温度的拟合直线在该位置处的温度突变值。为了更好地对比不同温度环境对于含缺陷界面热导的影响,在界面热导的基础上定义一个相对热导的概念: 在相同温度条件下,某缺陷浓度的界面热导和该温度下无缺陷的界面热导的百分比比值。

图4 温度梯度Fig.4 Temperature gradient

图5 热流分布Fig.5 Heat flow distribution
1.3 声子态密度
利用声子态密度(phonon density of state,PDOS)[26]揭示声子热输运的本质是一种用来表征二维材料中声子活动的方法,在体系稳定后,通过计算原子速度自相关函数的傅里叶变换得到的,公式如下[13]:
式中:ω代表频率;VACF(t)是速度自相关函数,其公式为:
式中:vi(0) 是第i个粒子在某时刻t关于速度的矢量;N是选中区域的原子数;〈〉表示速度的集合平均。
2 结果与讨论
2.1 单空位缺陷位置的影响
各位置缺陷的浓度与界面热导的关系如图6所示。由图6 可见, 当界面处h-BN 一侧近界面存在单空位缺陷时,缺陷的位置与浓度对界面热导的影响较为显著。例如, CB 与CN 界面处出现单空位缺陷时,随着缺陷浓度从0%增加到0.06%,界面热导分别从8.98 GW/(m2·K)、14.46 GW/(m2·K) 下降至6.85 GW/(m2·K)和8.44 GW/(m2·K),下降幅度分别为23.62% 和41.64%。随着缺陷浓度上升, 界面热导呈现近线性的下降趋势。这是因为单空位缺陷引起了界面声子弹道传输削弱和声子非弹性散射增加。在材料的平均声子自由程内,声子主要以弹道方式进行传输,这意味着声子在传播过程中几乎不会被晶格缺陷、掺杂等散射, 这种输运方式有利于声子的热输运活动; 而声子在非弹性散射的过程中会发生能量耗散,从而影响声子热输运活动[27]。接下来研究h-BN 一侧近界面处3 种位置的单空位缺陷,当浓度从0%增加到0.06%后,离界面最近的CB-NV2 与CN-BV2 两种单空位缺陷的界面热导分别下降至5.79 和8.19 GW/(m2·K),下降幅度超过界面处2 种单空位缺陷, 分别为35.44% 和43.34%。当缺陷位置逐渐远离界面, CB-BV3、CNNV3、CB-NV4 和CN-BV4 的界面热导的下降幅度不断增大,CB-NV4、CN-BV4 的界面热导为5.36 和7.12 GW/(m2·K),该位置下降幅度最大,分别达到了40.25%, 50.76%。由此推断, 当缺陷位置远离界面,界面热导随着距离增加而下降。因为当h-BN 一侧近界面出现缺陷时,其位置越接近h-BN 纳米带的中部,h-BN 中的声子弹道输送越受其影响,即长程声子被空位缺陷散射,削弱了声子在h-BN 的二维平面内进行热输运的能力, 从而影响h-BN 与石墨烯界面的声子耦合,降低了界面热导。PDOS 由平面横向声学声子(transverse acoustic,TA)、平面纵向声学声子(longitudinal acoustic, LA) 以及平面外声学声子(out-of-plane acoustic,ZA)3 个部分组成,其中TA 和LA 组成面内PDOS, 主导面内声子热输运的性能,即50THz 附近的高频区。而ZA 代表面外的声子散射,分布在PDOS 中的低频区内(0~10 THz)[28]。在此以CB 界面为例深入探讨声子活动的变化。

图6 不同位置的单空位缺陷浓度对ITC 的影响Fig.6 Effect of the concentration of single vacancy defects at different locations on the ITC
图7 是CB 界面B 原子在界面无缺陷和4 种位置的单空位缺陷时计算得到的PDOS。与无缺陷界面相比, 在10~20 THz 中CB-NV2、CB-BV3 和CB-NV4 的波峰逐渐升高,这是因为h-BN 中单空位缺陷的位置会影响声子活动,即由于声子在材料内部以弹道的方式进行热输运,在材料的声子平均自由程内,弹道长度越长,声子热输运性能越佳。因此,当缺陷位置逐渐靠近材料中心,声子的弹道输运受到影响,部分声子会在不改变输运方向或者以较小的角度改变输运方向通过缺陷界面,而其余声子的传输会偏离弹道较大的角度散射。所以缺陷位置远离界面削弱了界面声子耦合,降低了界面热导。
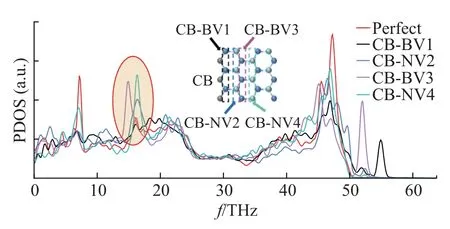
图7 无缺陷与各种缺陷位置下CB 界面B 原子的PDOSFig.7 PDOS of boron atoms at the CB interface at various defect positions
2.2 Stone-Wales 缺陷位置的影响
界面热导随SW 缺陷浓度的变化曲线如图8所示。首先观察4 类界面处SW 缺陷对于界面热导的影响, 由图8 可见, 这4 类位置的缺陷浓度升高时, 界面热导先下降, 后趋于收敛。以CN 界面上的CN-CNW1 与CN-CCW1 为例, 当缺陷浓度从0%上升至0.08%,界面热导从14.46 GW/(m2·K)分别下降至7.24 GW/(m2·K) 和8.60 GW/(m2·K)。而后, 当浓度增加至0.1%, 界面热导分别下降至7.18 GW/(m2·K) 和8.26 GW/(m2·K), 下降的幅度明显放缓,这是因为SW 缺陷的存在仅增强了面外声子散射, 而不影响原子间共价键的数量, 而共价键在声子的面内热输运活动中发挥主导作用[27]。接下来关注近界面的CB-CCW2 和CN-CCW2 的缺陷浓度对界面热导的影响,从图8 中可以看出,CB-CCW2与CN-CCW2 关于缺陷浓度的界面热导函数走势和界面处2 类SW 缺陷相似, 但略有不同的是, 在CN 界面上,CN-CCW2 在低浓度(0.02%~0.04%)时的界面热导低于CN-CBW1 和CN-CCW1。这是由于当石墨烯一侧出现SW 缺陷时,近界面的石墨烯失去了其原本理想结构下的有效散射体特性,导致界面热导的降低。而CB-CCW2 的界面热导并未显著表现出相似的变化,这可能是因为其界面热导数值较低,容易受到计算方法和舍入误差等因素的影响。较为明显的是,CB-CCW2 与CN-CCW2 在高浓度(0.1%)时的界面热导的值大于界面处2 种SW 缺陷,分别为6.70 和8.52 GW/(m2·K),这表明SW 缺陷在近界面对界面热导的影响小于界面处。

图8 不同位置的Stone-Wales 缺陷浓度对ITC 的影响Fig.8 The concentration of Stone-Wales defects effects to ITC at different locations
而h-BN 一侧的SW 缺陷的界面热导走势与其他3 种位置截然不同。CB-BNW2 和CNBNW2 的界面热导在0%~0.04% 内变化较小, 仅从8.98 GW/(m2·K)和14.46 GW/(m2·K)下降到8.01 GW/(m2·K)和13.73 GW/(m2·K),这是因为当近界面出现少数SW 缺陷时,其原子之间的共价键类型发生了部分改变,1 个SW 缺陷出现的同时伴随着2 个B—N 键被B—B 键和N—N 键取代,而由于键长和相邻的原子质量等因素影响[29],这2 种键对于热输运的贡献大于C—C 键和B—N 键。因此当少量的SW 缺陷出现后,界面热导下降幅度较小。
但随着浓度继续增加, 界面热导的下降趋势陡然变大,且并未在样本浓度内表现出收敛的趋势,在此引入褶皱机制来解释这种异常的变化。褶皱是由于二维材料中存在一定程度的缺陷,引起了晶格振动的非简谐效应,结构出现非晶化振动,进而导致材料平面在面外起伏。界面热导下降的本质原因是强烈的声子局部化现象导致声子被迫集中在褶皱的波峰和波谷之间的区域内[30]。此外,褶皱也在一定程度上引起了较强的局部声子散射。如图9 所示, 以CB 界面为例, 绘制了充分驰豫后几种不同位置的SW 缺陷在石墨烯/h-BN 的近界面区域中所引起的褶皱情况。从图9 中可以明显看出,当缺陷浓度逐渐升高, 存在CB-BNW2 缺陷的石墨烯/h-BN 近界面区域的褶皱现象愈加强烈,这种强烈的声子局部化现象降低了异质结构界面间声子的热输运性能,导致了界面热导的下降。而在同样的缺陷浓度下,CB-CBW1 和CB-CCW2 近界面并未出现明显褶皱。这揭示了h-BN 一侧存在SW 缺陷时界面热导异常下降的现象,为面内异质结构近界面拓扑缺陷对热输运的影响提供了一定的理论指导。

图9 在充分驰豫后,具有Stone-Wales 缺陷的石墨烯/h-BN 的近界面区域褶皱: (a)~(d)h-BN 一侧0%~0.08%浓度SW 缺陷的石墨烯/h-BN;(e)~(f)CB 界面、近界面石墨烯一侧0.28%浓度SW 缺陷的石墨烯/h-BNFig.9 Folds in the near-interface region of graphene/h-BN with Stone-Wales defects after sufficient relaxation: (a)-(d)graphene/h-BN with 0%-0.08% concentration of SW defects on the h-BN side; (e)-(f) 0.28% concentration of SW-deficient graphene in CB interface and near-interface of Graphene/h-BN
2.3 温度效应
由于CN 界面与CB 界面出现单空位缺陷时,两者对于界面热导的影响相仿,且CN 界面上出现N原子的单空位缺陷时,界面热导对缺陷浓度的变化更加敏感。因此选取CN 界面的N 原子单空位缺陷作为研究温度效应的观察样本。由图10 可知,一方面,当温度逐渐升高时,所有缺陷浓度下的界面热导均伴随温度升高而增加。其原因在于: 随着温度升高,更多高频声子被激发,这使得声子对于界面热输运产生了更大的贡献[27]。另一方面,随着N 原子的单空位浓度缺陷不断升高, 4 种温度环境下的界面热导均表现出近线性的下降趋势。

图10 不同温度下单空位缺陷浓度对ITC 的影响Fig.10 Effect of single vacancy defect concentration on ITC at different temperatures
为了深入了解含缺陷异质界面的热输运活动与温度的关系, 在此引入相对热导。由图11 可知, 当温度从300 K 上升到600 K,各浓度的相对热导均不断下降。以0.1%缺陷浓度为例,300~600 K 的相对热导分别为38.77%、38.58%、35.78%、33.63%, 这和图10 中温度与界面热导的关系截然不同。尤为明显的是,当600 K 温度下界面开始出现单空位缺陷(0.02%)时,相对热导的下降十分突兀,从19.96%下降到14.47%,相对热导下降约28%。这表明温度升高虽然可以激发更多的高频声子,促进声子进行面内热输运,但由于界面上存在缺陷,高频声子更容易在通过缺陷时发生面外散射,加剧了声子热输运的无序性,减弱了声子的热输运能力,在一定程度上降低了界面热导[13,31]。此外,这种突兀的变化也可能由边界散射、计算方法等原因引起。因此,温度升高对于含缺陷的石墨烯/h-BN 面内异质结构的界面热导有明显的提升作用。与此同时, 由于缺陷对高频声子的散射作用,这种提升作用又受到一定程度的削弱。

图11 不同温度下单空位缺陷浓度对相对热导的影响Fig.11 Effect of single vacancy defect concentration on relative thermal conductance at different temperatures
3 结 论
研究采取非平衡分子动力学方法对石墨烯/h-BN 平面异质结构中h-BN 一侧的单空位缺陷,与近界面中SW 缺陷的缺陷浓度对界面导热的影响进行了研究。结果证明,当h-BN 一侧出现单空位缺陷时, 由于缺陷位置影响了声子弹道传输, 随着缺陷位置逐渐远离界面,界面热导随之降低,在0.1%浓度下最低可以达到5.36 和7.12 GW/(m2·K)。而近界面中SW 的缺陷则根据共价键类型不同,对界面热导的影响出现差异化。石墨烯一侧的C-C 键SW 缺陷会与界面SW 缺陷呈现相似的先下降后收敛的趋势,这是因为SW 缺陷不会减少对面内声子热输运起主导作用的共价键。而BN 一侧则因为SW 缺陷引起了原子质量的无序排列,使得近界面区域内出现强烈的褶皱现象,界面热导在样本浓度内不断下降。此外, 还研究了温度变化对含单空位缺陷的界面的声子热输运的影响,随着温度从300 K 升至600 K,各缺陷浓度下的界面热导均有所升高,其本质是温度升高激发了更多高频声子参与热输运。但从相对热导的角度观察,随着温度升高,相对热导又会降低,这说明高频声子更易在穿过空位缺陷时发生散射。以上结果表明, 通过改变单空位缺陷与SW 缺陷的位置,或者调整温度,对于石墨烯/h-BN 面内异质结构的热输运特性都有显著的调节作用。这为微电子领域中开发高效、可控的新型材料提供了理论参考。
由于目前缺乏二维面内异质结构界面热导的实验表征手段,未来应当探索低维材料的热导率测量方法,可以从实际上印证和提高原子势函数的精度,有效提升分子动力学模拟的可信度与实用性。
