基于马尔可夫决策过程的轨道不平顺维修策略研究

何祥国 张斌 曾城林 邹海浪 罗雁云

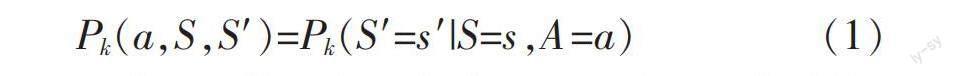
摘要：為有效判别轨道几何状态、适应高速铁路养护状态修，开展轨道不平顺维修策略优化研究。选取马尔可夫决策过程，设置轨道状态等级、维修动作空间和维修动作成本等模型参数，利用价值迭代算法进行求解，实现高速铁路线路维修计划的有效制定。以华东地区某有砟高速铁路线路为例，结合典型劣化速度的轨道单元区段特征，分析马尔可夫决策模型的维修决策优化过程并验证效果，同时探究轨道单元区段在每个决策时刻的最优维修决策，利用蒙特卡洛法模拟规划周期内的维修总成本并与实际维修成本进行对比。结果表明：基于马尔可夫决策过程的轨道不平顺维修决策，能够充分考虑轨道单元区段不平顺劣化的异质性，可以根据轨道单元区段的实际状态和劣化规律科学安排维修活动，提高维修作业的空间分辨率，规划周期内维修决策的优化效果显著，在保证线路高平顺性的同时减少维修成本，对铁路线路轨道养护维修具有指导作用。

关键词：高速铁路；轨道不平顺；马尔可夫决策过程；价值迭代算法；养护维修策略

中图分类号：U213 文献标志码：A

本文引用格式：何祥国，张斌，曾城林，等. 基于马尔可夫决策过程的轨道不平顺维修策略研究[J]. 华东交通大学学报，2023，40（5）：68-75.

Research on Maintenance Strategy of Track Irregularity Based

on Markov Decision Process

He Xiangguo1， Zhang Bin2， Zeng Chenglin2， Zou Hailang3， Luo Yanyun4

（1. Jiangxi Tongji Construction Project Management Co.， Ltd.， Nanchang 330025， China； 2. State Key Laboratory of Performance Monitoring and Protecting of Rail Transit Infrastructure， East China Jiaotong University， Nanchang 330013， China； 3. Nanchang High-speed Railway Infrastructure Section， China Railway Nanchang Bureau Group Co.， Ltd.， Nanchang 330100， China; 4. Institute of Railway and Urban Mass Transit， Tongji University， Shanghai 201804， China）

Abstract：In order to effectively judge the geometric state of track and adapt to the maintenance state of high-speed railway， the optimization of track irregularity maintenance strategy is studied. The Markov decision process is selected， the model parameters such as track state level， maintenance action space and maintenance action cost are set， and the value iteration algorithm is used to solve the problem， so as to realize the effective formulation of high-speed railway line maintenance plan. Taking a ballasted high-speed railway line in East China as an example， combined with the characteristics of the track unit at typical deterioration speed， the maintenance decision optimization process of the Markov decision model is analyzed and the effect is verified. At the same time， the optimal maintenance decision of the track unit section at each decision time is explored. Monte Carlo stochastic simulation is used to simulate the total maintenance cost in the planning cycle and compare it with the actual maintenance cost. The results show that the track irregularity maintenance decision based on Markov decision process can fully consider the heterogeneity of track unit section irregularity deterioration， scientifically arrange maintenance activities according to the actual state and deterioration law of track unit section， improve the spatial resolution of maintenance operation， and the optimization effect of maintenance decision in the planning cycle is remarkable， which reduces the maintenance cost while ensuring the high smoothness of the line， and has a guiding role in the maintenance and repair of railway track.

Key words： high-speed railway; track irregularity; Markov decision process; value iteration algorithm; maintenance strategy

Citation format：HE X G，ZHANG B，ZENG C L，et al. Research on maintenance strategy of track irregularity based on Markov decision process[J]. Journal of East China Jiaotong University，2023，40（5）：68-75.

我国高速铁路现行的养护维修模式主要包括故障修和周期修，这两种模式下的养护维修计划通常线路的修理时间和修理方式较为固定[1-2]。维修决策主要依据轨道几何不平顺指标进行制定，当轨道几何不平顺指标值超过管理值时，将立即进行不同等级的线路修理。然而，实际运营中，线路状况尤其是轨道单元的劣化速度存在差异，维修策略不适用引起的“过维修”和“欠维修”情况时常发生，导致有些线路状況良好却仍进行维修、有些状况异常反而未进行维修。可见，维修决策的实施属于被动性管理，缺乏对轨道状态的有效预判，造成延误最佳的维修时机，增大了养护维修工作量与维修成本。

为提高维修质量水平，实现由粗放管理向精准施策转变，国内外学者从不同角度探讨线路维修决策模型及相关理论，主要分为以下三类：一是以线路设备服役状态为核心构建维修决策模型，考虑不确定性条件下的轨道结构实时服役状态[3-8]；二是将维护成本费用最低作为模型最优化目标，使用动态规划与强化学习等数学工具辅助制定线路维修策略[9-12]；三是综合考虑多个优化目标的维修决策模型，以轨道几何状态、维修作业成本等多种集合为目标函数建立维修决策模型[13-19]。

目前，上述研究中设定的维修作业区间长度通常较长，鲜有考虑不同空间位置轨道单元区段轨道几何形位劣化的异质性，未对劣化速度不同的轨道单元进行区分，现场维修作业精准度有限。

本文以有砟高速铁路线路为例，将连续的轨道区段分割为维修决策单元，利用马尔科夫决策过程建立研究模型，提出适合不同轨道单元区段的维修策略，实施精细化维修作业，使维修活动更加经济合理，对实现维修策略科学化与可持续及其在铁路线路养护维修中的应用具有借鉴意义。

1 马尔可夫决策过程模型

1.1 模型介绍

马尔可夫决策过程是一种强化学习算法，由五元组（S，A，Pk，R，γ）构成，其中，S称为状态空间即各种状态的集合，A称为动作空间即各种可能执行动作的集合，R为在状态转移过程中得到的奖励，γ为折扣因子，S′为转移后状态空间。轨道单元区段k在某一状态s下采用动作a而转移到状态s′的概率为

马尔科夫决策过程中的任意一个决策时刻，决策者（智能体）采用动作空间中某一动作，使决策过程以一定的概率由当前状态转移到下一状态，并在该过程中得到相应的奖励，奖励起着指引智能体学习的作用。同时，目标是找到一个最优的策略函数，也即要找到一个最优策略来最大化随机过程中的累积奖励。马尔可夫决策过程中智能体与环境之间的交互示意见图1。

1.2 模型构建

为充分考虑轨道单元区段劣化过程中的异质性，以一段有砟高铁线路为例，划分150个200 m的轨道单元区段，并按照里程顺序依次编号为1～150。构建马尔可夫决策过程模型，对其维修决策进行优化，模型参数设置方法如下。

1） 轨道状态等级划分。将轨道质量指数TQI作为轨道不平顺状态的评价指标，并根据每个轨道单元区段的TQI值确定各轨道单元区段的不平顺状态等级，其中主要参考《高速铁路有砟轨道线路维修规则（试行）》[20]中的T值评分法进行划分。T值评分法中的TQI扣分规则见表1，按照超过管理值10%和超过管理值20%将轨道不平顺状态划分为5个等级，即状态空间S={1，2，3，4，5}，具体状态等级划分见表2。

2） 维修动作空间。结合高速铁路现场作业需求，将高速铁路有砟轨道的轨道不平顺修理活动类型，确定为不做维修（a1=0）、经常保养（a2=1）和线路大修（a3=2），即动作空间表述为A={a1，a2，a3}。

3） 维修动作成本。当轨道不平顺状态处于不同的状态等级时，养护维修费用与所执行的维修工作量相匹配，为尽可能反应真实情况，设置维修费用构成如下：

① 轨道检测费用ci，在任意决策时刻，对轨道进行几何形位状态检测所产生的费用；

② 经常保养费用cmin，在轨道不平顺状态等级处于s时，周期时间内对轨道进行日常巡检、清扫和保养，保持轨道健康状态所产生的费用；

③ 线路大修费用cmaj，以解决钢轨伤损疲劳、道床脏污和板结为重点，按周期有计划地对设备进行更新、改善和全面修理所产生的费用；

④ 风险成本cr，采用维修动作A后轨道所处的状态，即维修后轨道不平顺状态等级高则风险成本大、等级低则风险成本低。

采用不同的维修动作，对应的轨道不平顺改善程度不尽相同，且即使采用同一维修动作，也存在一定概率导致轨道不平顺状态转移到不同状态等级。因此，对维修效果进行量化表征，使用风险成本量化维修动作的质量水平。

根据现场调研情况，不同轨道不平顺状态等级时，轨道单元区段采取相应维修动作成本见表3。

综上，轨道单元区段的轨道不平顺状态等级为S时，采取维修动作A后，所产生的成本函数C（S，A）如式（2）所示

4） 状态转移矩阵。考虑到各个轨道单元区段劣化速度并不相同，且执行不同维修动作时对轨道几何形位将产生不同影响，因此，需要单独计算各个轨道单元区段在执行不同维修操作情况下的状态转移矩阵。根据轨道检测数据和维修操作记录，状态转移矩阵计算如式（3）所示

式中：S为轨道不平顺当前状态；S′为轨道不平顺转移后状态；A为采取的维修动作；N为处于S状态的轨道单元数目；NSS′A为轨道单元区段在采取动作A时从状态S转换到状态S′的次数；NSjA为轨道单元区段在采取动作A时从状态S转换到其他状态的次数。

1.3 模型求解

利用马尔可夫决策过程建立模型时，尤其是在状态空间较小时，价值迭代算法可以快速收敛，因此，本文使用价值迭代算法对模型进行求解。在价值迭代算法中，综合成本的迭代方程采用贝尔曼方程进行迭代，计算如式（4）所示

式中：Vπ（s）为轨道单元区段在状态s时使用策略π所产生的价值；C（s，a）为轨道单元区段在状态s时采用动作A所产生的维修成本；γ为折扣系数；p（s′|s，a）为轨道单元区段状态在采用动作a后转移到状态s′的概率；Vπ（s′）为轨道单元区段在状态s′时使用策略π所产生的价值。价值迭代算法过程见表4。

综上，迭代算法思路归纳为：首先，初始化每个状态下的状态价值函数，令每个动作价值函数的值为0；其次，采用贝尔曼方程进行迭代计算状态价值函数，并用贪婪策略对每次迭代的策略进行改进，一直迭代到此次的价值函数和下一次迭代的价值函数之差小于設定阈值时结束迭代，并输出最优策略。

2 算例分析

2.1 数据准备

华东地区某高速铁路有砟轨道线路设计时速250 km/h，测试车辆为高速综合检测列车，采样间隔为0.25 m，轨道检测频率为每月一次。收集线路下行线方向2016年2月—2021年12月期间共计71次轨检车动态检测数据和6年的年度修理计划。

2.2 决策优化过程分析

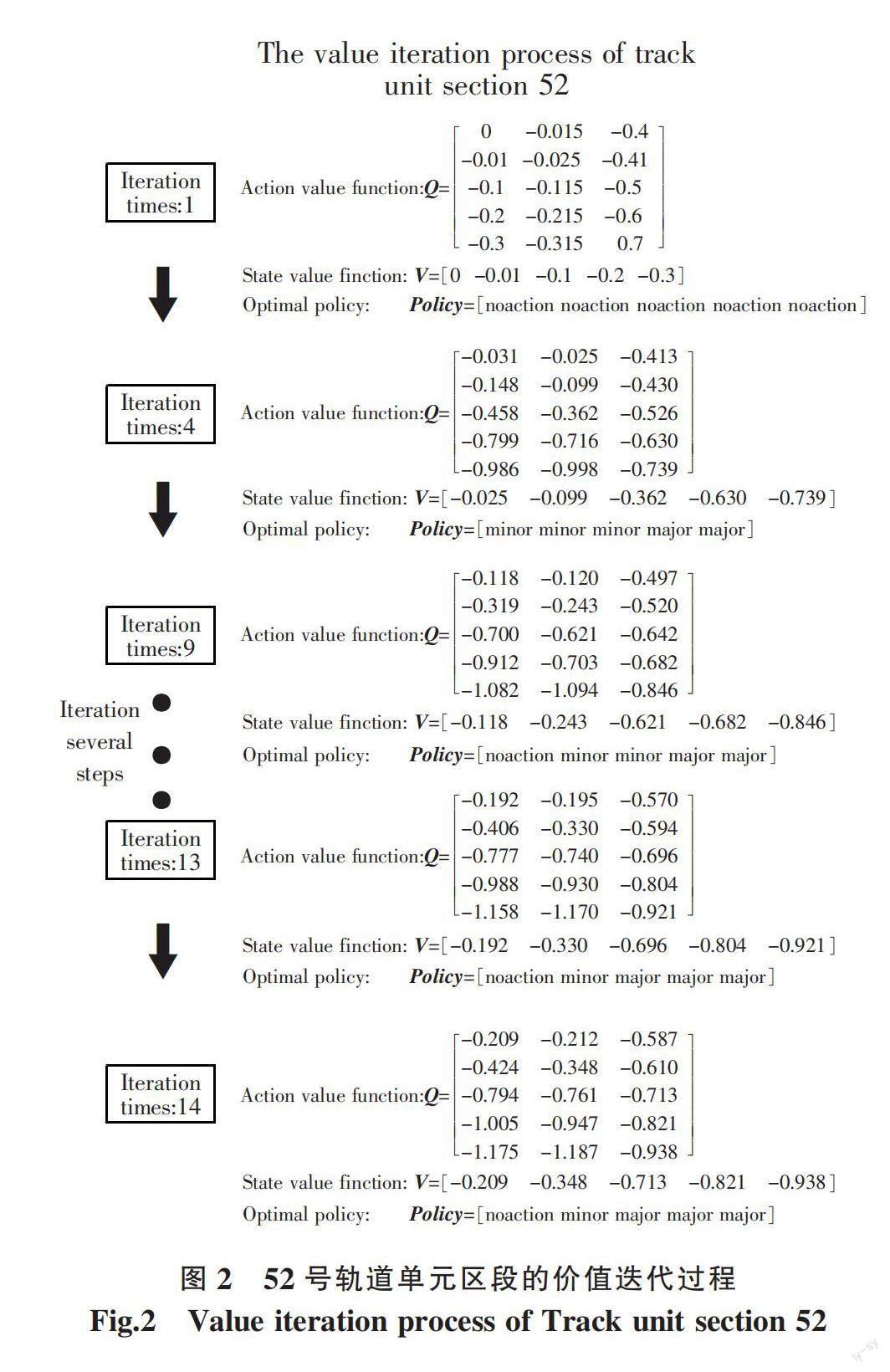
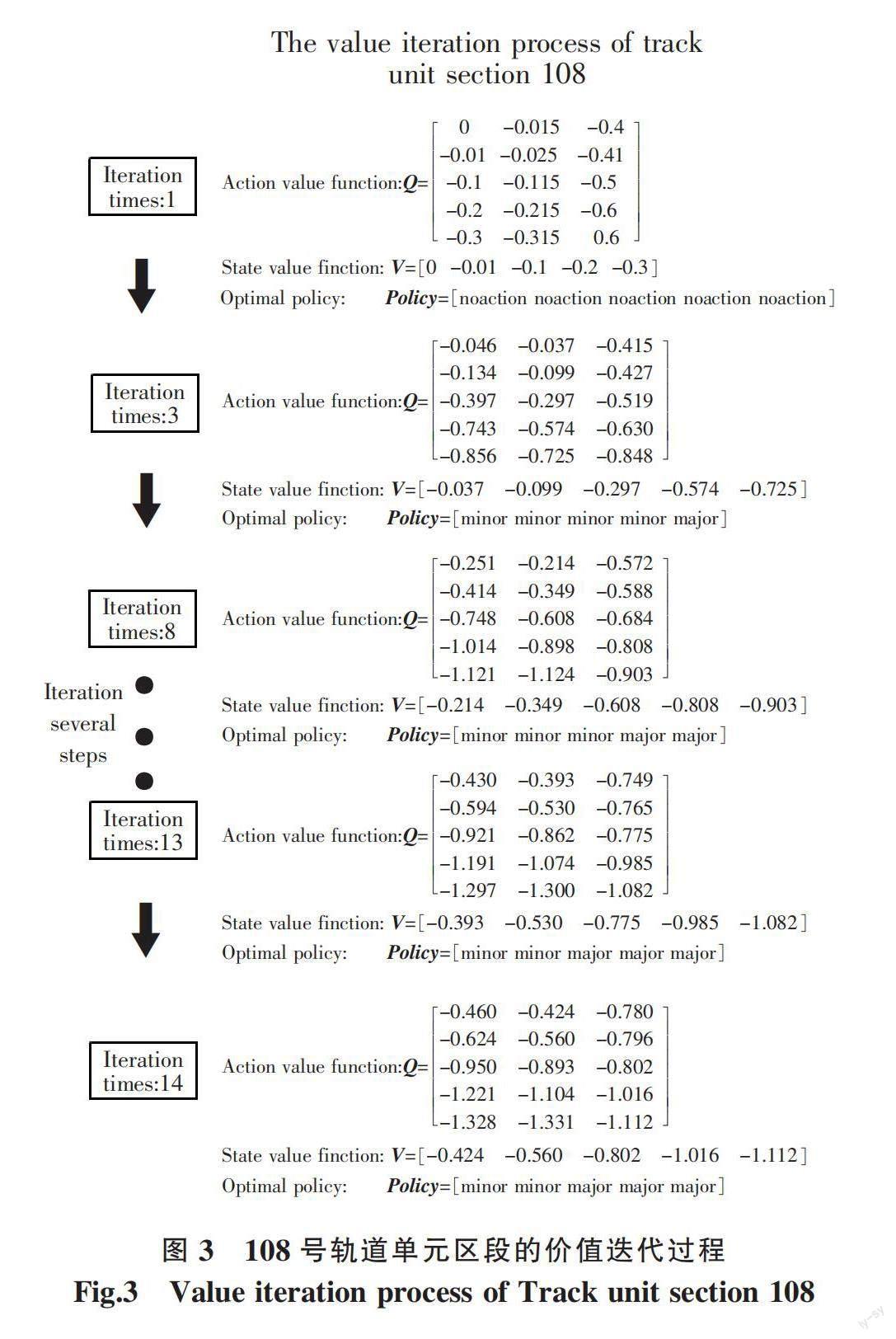
以2个典型劣化速度的轨道单元区段为例，52号和108号分别为劣化速率较慢和较快的轨道单元区段，说明价值迭代算法的迭代过程和决策优化效果，具体求解方法和迭代过程分别见图2和图3。由于设置的动作价值函数初始值为0，故52号和108号轨道单元区段在第1步迭代所得结果相同。

从图2可以看出，智能体进行迭代时，会根据每个状态下的动作价值函数最大值挑选出最优动作。在此规则下，智能体在第1步迭代后的选择是无论轨道不平顺处于何种状态均不做维修。随着迭代步数的增加，迭代到第4步时，通过与环境交互得到奖励函数的反馈，智能体更新最优决策，在状态1，2，3时执行经常保养操作（minor），在状态4，5时执行线路大修操作（major）。当迭代进行到第13步时，智能体采取的最优策略是在状态1时不进行任何操作，在状态2时执行经常保养操作，在状态3，4，5时执行线路大修操作。模型的决策在第13步之后的迭代过程中一直没有发生变化，说明模型已经收敛，所得策略为此环境下的最优策略。

换言之，第13步迭代产生的策略，即在状态为1时，智能体判断该区段的劣化速度较慢，且状态升高的风险不大，为使维修成本最低，故选择不进行任何操作；在状态为2时，智能体判断维持轨道状态现状并防止不断劣化至维修管理阈值，结合考虑维修成本，选择执行经常保养操作；在状态为3，4，5时，轨道单元区段TQI值已经超过规范中规定的阈值，此时，智能体判断轨道状态较为危险，以改善轨道不平顺状态为目标，选择执行线路大修操作。

从图3可以看出，在108号轨道单元区段迭代过程中，经过13步迭代，模型达到收敛，最优决策为：在状态1，2时，智能体判断该环境下轨道的劣化速度较快，有较大可能短时间内完全劣化到状态2，选择执行经常保养操作；在状态3，4，5时，智能体判断轨道状态较危险，故均执行线路大修操作。对比图2可以看出，智能体对不同劣化速度的轨道单元区段所做出的决策是不相同的，随着迭代次数的增加，智能体在与环境的交互中不断得到反馈，最终做出的决策也变得越来越合理，最优维修策略也比较符合工程实际需要。

2.3 规划周期内维修决策的优化效果

为更好地观察轨道单元区段维修策略在整个维修规划周期中的影响，分析上述2个典型轨道单元区段在规划周期内的每个决策时刻采用的最优维修动作，并与实际决策进行对比，结果见图4。

可以看出，由于52号轨道单元区段的劣化速率较慢，轨道几何状态较好，相比于实际决策选择大修时，在绝大部分情况下模型都选择执行经常保养动作；实际决策选择经常保养时，在少数决策时刻模型为使成本最优而选择不做维修。相比之下，108号轨道单元区段的劣化速率较快，在大多数时刻模型选择经常保养动作，这与实际决策相同，但是，选择执行大修操作的决策时刻较实际决策少，因此，模型计算的维修决策较实际决策所产生的维修成本低。

2.4 决策时刻的最优维修决策

本算例的轨道区段维修规划周期为2年，根据调研，现场每个月利用轨检车对下行线的轨道不平顺状态进行检测，因此，规划周期内共计24个决策时刻。利用价值迭代算法，对2020—2021年期间下行线的150个轨道单元区段维修决策进行优化，可以得到各个轨道单元区段在每个决策时刻的最优维修决策。现选取2020年2月作为起始决策时刻，该月的模型计算维修策略与实际维修策略对比见图5。

从图5可以看出，模型计算所得维修策略和实际使用策略的对比情况，实际维修策略一般是挑选轨道几何形位状态差的连续区段，这些区段中存在多处TQI值超出了管理阈值8，进而采取大修操作，但是这些区段中也有一段（127～129号）其TQI值和轨道状态等级并不高，也误采取了大修的维修策略。同时，某些状态良好、TQI值较低且劣化速度较慢的区段，也误采取了经常保养修理的策略，且这类区段数量不在少数。此外，在一些轨道几何形位状态不好的区段，如75号和76号轨道单元区段，并未采取大修，而是误采取了经常保养操作。

通过马尔可夫决策过程模型计算出的轨道不平顺维修决策，能够根据不同轨道单元区段的劣化趋势，科学安排修理活动，各类维修数量对比见表5。轨道几何形位状态良好的轨道单元区段，可以少维修甚至不维修，并对需要进行线路大修的轨道区段进行了更加精细的划分，这将减轻铁路工务部门的养护维修工作量并减少维修成本。

2.5 与实际维修决策成本的对比分析

利用蒙特卡洛随机模拟方法，将马尔可夫决策过程模型通过计算得到在规划周期内的维修总成本，并将其与实际维修成本进行对比。

轨道单元区段状態转移矩阵中的马尔科夫链，服从概率分布，具有随机性。即使确定了决策时刻的维修策略，模拟执行相同的维修操作后，也可能导致轨道不平顺状态转移到不同的等级。因此，一次计算所得的成本无法反映出计算所得策略的真实成本。这里，在确定维修策略后，进行1 000次的蒙特卡洛模拟，计算其所需成本的期望值，模拟得到的周期总成本以及结果分析见图6。

从图6可以看出，模拟该轨道区段维修规划周期的维修总成本最大值为198.26万元，最小值为136.65万元，平均值为167.41万元。根据现场维修作业调研结果，该车间对本区段在2年时间内的线路检测、经常保养及线路大修等维修总成本约186万元。由此可见，本文模型制定的维修策略在保障线路高平顺性的同时可以显著降低维修成本。

3 结论

本文结合轨道不平顺特征，提出一种基于马尔可夫决策过程的轨道维修决策模型。通过设置轨道状态等级、维修动作空间和维修动作成本等模型参数，利用价值迭代算法，从多个维度分析轨道单元区段在每个决策时刻的最优维修决策。最后，利用蒙特卡洛法模拟规划周期内的维修总成本，并与实际维修成本进行对比。

1） 通过马尔可夫决策过程模型优化后的轨道不平顺维修决策，可以充分考虑不同轨道单元区段不平顺劣化的异质性，提高维修的空间分辨率。

2） 随着迭代次数的增加，智能体通过与环境交互不断得到奖励函数的反馈，最终做出的维修决策变得越来越合理，更加符合工程实际需要。

3） 规划周期内维修决策的优化效果显著，依据轨道单元区段实际状态和劣化规律科学安排维修活动，在保证线路高平顺性的同时降低了维修成本。

参考文献：

[1] 徐伟昌. 大型养路机械捣固作业维修决策模型研究[J]. 铁道科学与工程学报，2016，13（1）：152-157.

XU W C. Maintenance decision model based on large machinery tamping work[J]. Journal of Railway Science and Engineering，2016，13（1）：152-157.

[2] 陈立. 制定状态修基准指标指导大型养路机械捣固作业的探讨[J]. 铁道建筑，2015，2（2）：118-121.

CHEN L. Discussion on the formulation of state repair benchmark index to guide the tamping operation of large road maintenance machinery[J]. Railway Engineering，2015，2（2）：118-121.

[3] 李茂圣，王大彬. 一种智慧地铁轨道状态预测和维修决策优化系统[J]. 计算机测量与控制，2023，31（2）：48-54.

LI M S，WANG D B. Intelligent subway track state prediction and maintenance decision-making optimization system[J]. Computer Measurement & Control，2023，31（2）：48-54.

[4] PAPAKONSTANTINOU K G，SHINOZUKA M. Planning structural inspection and maintenance policies via dynamic programming and Markov processes. Part II：POMDP implementation[J]. Reliability Engineering and System Safety，2014，130：202-213.

[5] 郭然. 铁路线路养护维修计划编制理论与方法[D]. 北京：北京交通大学，2015.

GUO R. Theory and method for railway track maintenance scheduling[D]. Beijing：Beijing Jiaotong University，2015.

[6] FAMUREWA S M，XIN T，RANTATALO M，et al. Optimization of maintenance track possession time：A tamping case study[J]. Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2015，229（1）：12-22.

[7] 杨雅琴，徐鹏，吴细水. 基于Fast-MCD的自适应建模探索轨道不平顺劣化[J]. 清华大学学报（自然科学版），2022，62（3）：516-522.

YANG Y Q，XU P，WU X S. Adaptive modeling method based on the Fast-MCD to analyze railway track irregularityDeterioration deterioration[J]. Journal of Tsinghua University（Science and Technology），2022，62（3）：516-522.

[8] 彭丽宇，张进川，苟娟琼，等. 基于BP神经网络的铁路轨道几何不平顺预测方法[J]. 铁道学报，2018，40（9）：154-158.

PENG Y L，ZHANG J C，GOU J Q，et al. Prediction method of railway track geometric irregularity based on BP neural network[J]. Journal of the China Railway Society，2018，40（9）：154-158.

[9] 徐菲，曲建军. 基于检测数据的高速铁路轨面沉降不平顺发展趋势预测[J]. 中国铁路，2017（10）：8-10.

XU F，QU J J. Prediction on development trend of settlement irregularity of high-speed rail surface based on test data[J]. China Railway，2017（10）：8-10.

[10] PENG F，OUYANG Y，SOMANI K. Optimal routing and scheduling of periodic inspections in large-scale railroad networks[J]. Journal of Rail Transport Planning & Management，2013，3（4）：163-171.

[11] 刘平. 基于遗传算法的线路大型养路机械捣固作业单元区段选择模型[J]. 铁道建筑，2022，62（8）：72-76.

LIU P. Selection model of tamping operation unit section of large maintenance machinery based on genetic algorithm[J]. Railway Engineering，2022，62（8）：72-76.

[12] NEUHOLD J，VIDOVIC I，MARSCHNIG S. Preparing track geometry data for automated maintenance planning[J]. Journal of Transportation Engineering，Part A：Systems，2020，146（5）：04020032.

[13] SHARMA S，CUI Y，HE Q，et al. Data-driven optimization of railway maintenance for track geometry[J]. Transportation Research Part C：Emerging Technologies，2018，90：34-58.

[14] SANCHO L C B，BRAGA J A P，ANDRADE A R. Optimizing maintenance decision in rails：A Markov decision process approach[J]. Journal of Risk and Uncertainty in Engineering Systems，Part A：Civil Engineering，2020，7（1）：1-19.

[15] BAI W F，WEI Y，CHANG Y Y，et al. Life cycle repair decision optimization model based on adaptive learning markov decision process of rail facility[J/OL]. Available at SSRN： 1-36（2022-3-23）[2023-8-26]. http：//dx.doi.org/10.2139/ssrn.4137913.

[16] 許玉德，赵梓含，乔雨，等. 大机捣固养修作业计划多目标决策模型[J]. 华东交通大学学报，2019，36（3）：55-63.

XU Y D ，ZHAO Z H，QIAO Y，et al. Multi-objective decision model for tamping maintenance plan of ballast track[J]. Journal of East China Jiaotong University，2019，36（3）：55-63.

[17] 许玉德，吴琰超，魏子龙，等. 基于放大系数和权重组合的无砟轨道TQI计算[J]. 华东交通大学学报，2021，38（5）：101-109.

XU Y D，WU Y C，WEI Z L，et al. Calculating TQI of ballastless track based on amplification coefficient and weights[J]. Journal of East China Jiaotong University，2021，38（5）：101-109.

[18] 卢春房. 高速铁路桥隧工程养修模式与关键技术[J]. 中国铁路，2017（7）：1-8.

LU C F. Maintenance and repair mode and technologies for high speed railway bridges and tunnels[J]. China Railway，2017（7）：1-8.

[19] 常艳艳，刘仍奎，王福田，等. 兰新线铁路轨道几何状态劣化短期预测模型研究[J]. 铁道学报，2020，42（11）：124-129.

CHANG Y Y，LIU R K，WANG F T，et al. Short-term prediction model for track geometry degradation on Lanzhou-Xinjiang railway[J]. Journal of the China Railway Society，2020，42（11）：124-129.

[20] 中国铁道科学研究院. 高速铁路有砟轨道线路维修规则[M]. 北京：中国铁道出版社，2013.

CHINA ACADEMY OF RAILWAY SCIENCES. Maintenance rules for ballasted track of high-speed railway[M]. Beijing：China Railway Publishing House，2013.

第一作者：何祥国（1964—），男，高级工程师，研究方向为土木工程管理及健康监测。E-mail：hexiangguo123@sina.com。

通信作者：张斌（1985—），男，副教授，硕士生导师，研究方向为轨道结构动力学。E-mail：zhangbin010@126.com。

（责任编辑：李 根）