轨距杆对重载铁路小半径曲线轮轨动力学性能影响

陈清华 閤鑫 胡晓宇 王开云

摘要：为探明轨距杆对重载铁路小半径曲线轮轨动力学性能影响，基于车辆-轨道耦合动力学理论，分析了机车以70 km/h的运行速度通过R300 m曲线时的轮轨动态相互作用和轮轨磨耗，系统对比分析了运行速度、曲线半径和轨距杆对机车通过小半径曲线时钢轨跨中轨距动态扩大量和轮轨磨耗数，进一步研究了轨距杆的布置间距对线路横向稳定性的影响。仿真结果表明：轨距杆能够加强轨道轨距保持能力并减小曲线外侧钢轨翻转角；相比未安装轨距杆的曲线，安装了轨距杆的曲线其内侧钢轨的接触点更靠近曲线内侧；机车通过有无轨距杆的小半径曲线时的轮轨磨耗数和轨距动态扩大量均随着曲线半径减小和运行速度增大而增大；增大轨距杆布置密度可以有效增强线路轨距保持能力，当轨距杆布置间距由4个轨跨减小至3个轨跨时，轨距动态扩大量将降低36.3%。

关键词：重载铁路；轨距杆；数值计算；轮轨动力学性能；小半径曲线；轮轨磨耗；车辆轨道耦合动力学

中图分类号：U231 文献标志码：A

本文引用格式：陈清华，閤鑫，胡晓宇，等. 轨距杆对重载铁路小半径曲线轮轨动力学性能影响[J]. 华东交通大学学报，2023，40（5）：1-9.

Influence of Gauge Rods on Wheel-Rail Dynamic Performance

in Tight Curves of Heavy-Haul Railway

Chen Qinghua，Ge Xin，Hu Xiaoyu，Wang Kaiyun

（State Key Laboratory of Rail Transit Vehicle System， Southwest Jiaotong University， Chengdu 610031， China）

Abstract：In order to investigate the influence of gauge rods on the dynamic performance in tight curves of heavy haul railway， the wheel-rail dynamic interaction and wheel-rail wear when the locomotive passed the R300 m curve at a running speed of 70 km/h were analyzed on the basis of vehicle-track coupling dynamic theory. The influence of running speed and curve radius on gauge dynamic expansion， wear number， and gauge rods were analyzed. Furthermore， the influence of the spacing of gauge rods on the lateral stability of the track was studied. The simulation results indicate that the gauge rods can stabilize the gauge and reduce the turning angle of the rail at the outside curve. Compared with the curve without gauge rods， the contact point of the inner rail of the curve with gauge rods is closer to the inner side of the curve. The wear number and the dynamic gauge expansion when the locomotive negotiates a tight curve will increase with the decrease of curve radius and the increase of running speed. Increasing the arrangement density of gauge rods can effectively enhance the ability to stabilize the gauge. The dynamic gauge expansion will reduce by 36.3% when the spacing of gauge rods is reduced from 4 to 3 rail spans.

Key words： heavy-haul railway; gauge rods; numerical simulation; wheel-rail dynamic performance; tight curves; wheel-rail wear; vehicle-track coupling dynamics

Citation format：CHEN Q H，GE X，HU X Y，et al. Influence of gauge rods on wheel-rail dynamic performance in tight curves of heavy-haul railway[J]. Journal of East China Jiaotong University，2023，40（5）：1-9.

近年來随着重载铁路上轴重和运行速度增加，机车通过小半径曲线时的轮轨动态相互作用不断增强。在恶劣的轮轨相互作用下钢轨压溃、侧磨[1]、接触疲劳等轮轨损伤问题日益凸显，严重降低了轮轨服役寿命，甚至危及重载列车行车安全。

国内外研究人员对小半径曲线轮轨动力学性能影响进行了大量理论和试验研究。陈雷等[2]开展了提速货车低速时通过小半径曲线的动力学试验。李敏等[3]通过仿真和试验分析了某型内燃动车组的动态曲线通过性能。王坤全[4]研究了采用径向转向架的提速货运机车在曲线上的动力学性能、牵引性能和通过性能。王娜娜等[5]分析了不同种类的轮径差对车辆小半径曲线通过性能的影响规律。史智勇等[6]研究了HSM型钢轨铣磨车以同速度条件下通过小半径曲线的轮轨安全性。刘文龙等[7]研究了悬挂式单轨车辆在曲线通过安全限速内通过不同半径曲线时的轮轨动态相互作用，轮轨安全性指标和平稳性指标。沈钢等[8]分析了初始与实测型面对地铁车辆曲线通过性能的影响，并分析不同的轮轨型面匹配对轮轨磨耗、钢轨波浪形磨耗、接触疲劳的影响。Liu等[9]通过仿真和试验分析了曲线地段轨道横向位移特性。刘锦辉等[10]建立了三维重载列车-轨道动力学模型，基于该模型分析了车钩力作用下列车通过曲线时的轮轨相互作用。折成林[11]研究了C80重载货车通过不同轨底坡设置条件下的小半径曲线时的轮轨接触特性、运行安全性和轮轨磨耗。许自强等[12]基于轮轨几何匹配关系、轮轨磨耗分析等方法研究了轮缘异常磨耗机理，并通过仿真和试验验证了提出的轮缘减磨措施。丁君军等[13]采用基于接触斑能量耗散理论的车轮踏面磨耗模型仿真分析了国内重载线路上货车车轮踏面的磨耗演化过程。李星等[14]基于Archard材料磨损模型分析了曲线半径、轮缘润滑及轮轨材料对小半径曲线钢轨侧磨和滚动接触疲劳的影响。马帅等[15]结合钢轨磨耗和线路运营等数据，建立了基于非线性自回归神经网络的曲线钢轨侧磨发展预测模型，提出了状态修和周期修相结合的曲线钢轨换轨策略。以上文献在小半径曲线轮轨动力学性能研究中均未考虑轨距杆作用。

轨距杆是一种连接轨道上内外钢轨以提高小半径曲线上钢轨横向稳定性的轨道强化设备。《普速铁路线路修理规则》（TG/GW 102—2019）规定了正线半径小于800 m的曲线需要安装轨距杆。毛帅等[16]通过试验发现在桥梁和线路过渡段分层次不等距安装轨距杆可使得路桥过渡段刚度更均匀，从而降低轮轨动态相互作用和钢轨磨耗。为此，本文基于车辆-轨道耦合动力学理论，考虑曲线上轨距杆的作用，建立机车-有砟轨道耦合动力学模型。基于该模型分析了机车通过小半径曲线时曲线上安装轨距杆对轮轨动力学性能和轮轨磨耗的影响，得到了不同半径和不同速度下机车通过有无安装轨距杆曲线时轮轨动力学性能的变化规律，并进一步研究轨距杆布置密度对线路轨距保持能力的影响。

1 机车-有砟轨道耦合动力学模型

1.1 机车和有砟轨道动力学模型

基于车辆轨道耦合动力学理论[17]，建立了考虑轨距杆的机车-有砟轨道耦合动力学模型（图1）。该模型主要包括机车模型、含轨距杆的有砟轨道模型和轮轨相互作用模型。模型中机车采用SIMPACK软件建立，轮轨相互作用模型中轮轨法向力和切向力分别采用Hertz弹性非线性接触理论和FASTSIM计算。轨道在SIMULINK软件中采用自编程方法建立。机车模型和轨道模型通过联合仿真方法实时交换数据实现耦合。

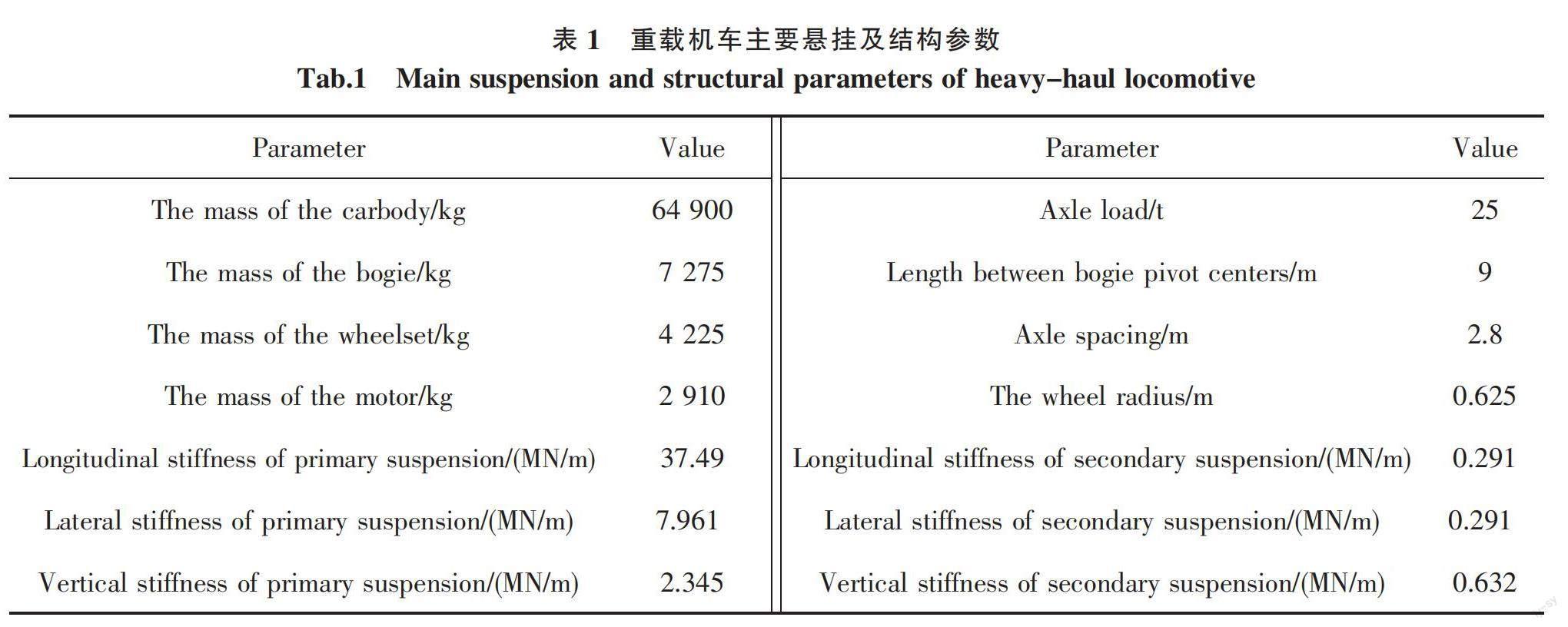
机车主要悬挂及结构参数如表1所示。机车模型包括1个车体、2个转向架、2个双杆推挽式牵引杆、4个轮对和4个架悬式牵引电机。模型中各部件均考虑为刚体，部件间通过弹簧阻尼力单元相互连接。其中牵引电机只考虑纵向、浮沉及点头3个自由度，牵引杆考虑除摇头外的5个自由度，其余部件均考虑6个自由度。

有砟轨道模型由钢轨、轨枕和道床的三层结构组成。钢轨采用连续弹性离散点支承的简支Timoshenko梁模拟，考虑其垂向、横向弯曲和扭转振动。钢轨横向的振动微分方程如下（垂向和扭转方程类似，此处不再赘述。）

式中：mr为单位长钢轨的质量；Yr和Ψy分别表示钢轨横向位移和绕y轴的截面转角变形；FLi是第i个支点的横向支反力；Qj是第j位车轮作用于钢轨的横向荷载；FGk是第k根轨距杆作用于钢轨的横向力；xi是第i个支点的坐标，xwj是第j位车轮坐标；xk是第k根轨距杆的坐标；Ns是钢轨支点数；Ng是轨距杆根数；Iz为钢轨截面对z轴的惯性矩；E为钢轨弹性模量；Gr为钢轨剪切模量；ρr为钢轨密度；Ar为钢轨截面面积；κy为钢轨横向截面的剪切因子。

轨枕考虑其横向、垂向和扭转自由度，道床仅考虑其垂向振动。钢轨与轨枕、轨枕与道床块和道床块与道床块之间均采用弹簧-阻尼单元连接。为体现机车运行在离散支承的钢轨上引起的周期性激励，采用了文献[18]中提出的移动窗口模型。

1.2 轨距杆模型

对于轨距杆，电气化铁路上采用的绝缘轨距杆可以看作是由三段圆杆连接而成，轨距杆一般安装在轨枕两跨之间，杆两端分别固定在左右轨的轨底（图2）。本文中将其简化为具有轴向拉压刚度和弯曲刚度的弹簧单元，其轴向拉压刚度Kt和弯曲刚度Kb分别为

式中：Eg为轨距杆的弹性模量；Ai为杆件的截面面积；li为杆件的长度；Ii为杆件截面的惯性矩。

1.3 模型验证

为验证所建立的考虑轨距杆的机车-轨道耦合动力学模型，在某重载铁路小半径曲线上开展了轮轨力测试。试验曲線的曲线半径为400 m，曲线超高为100 mm，圆曲线处每隔4根轨枕安装有一根轨距杆，如图2所示。试验中依据《轮轨横向力和垂向力地面测试方法》（TB/T 2489—2016）测试机车以65 km/h的速度通过曲线时的内外侧轮轨垂向力。采用建立的动力学模型计算相同工况下的轮轨垂向力，仿真与试验的对比结果如图3所示。可以看出，仿真模型计算的轮轨垂向力最大值与实测轮轨垂向力最大值之间的误差最大为3.7%，证明了所建立模型的可靠性。

2 轨距杆对轮轨动态相互作用影响

利用机车-有砟轨道耦合动力学模型，对比分析了轨道有无轨距杆时，机车通过不同曲线半径的轮轨动态相互作用特性和轮轨磨耗特征。仿真中机车运行速度分为70、80、90 km/h 3个等级，曲线选取R300、R400、R500、R600 m 4种不同半径的曲线。线路总长设置为500 m，其中缓和曲线和圆曲线设置为100 m，其余路段为直线。安装轨距杆的线路从进入圆曲线起每隔3个轨跨设置一根轨距杆，总共设置50根轨距杆。

2.1 轮轨动态响应

限于篇幅，此处仅给出机车以70 km/h的速度分别通过有无安装轨距杆的R300 m曲线时的一位轮对处的轮轨动态响应。如图4（a）所示，内外侧钢轨接触点在进入曲线后均向曲线外侧移动，在圆曲线上接触点位置横移量达到最大值约15.5 mm；对比圆曲线上有无轨距杆时内外侧钢轨上的接触点位置，可以看出外侧钢轨接触位置差别不大，安装轨距杆的内侧钢轨较未安装轨距杆的钢轨其轮轨接触位置靠曲线内侧约0.5 mm。图4（b）～图4（e）分别为机车通过有无轨距杆曲线时的内外侧轮轨垂向力、轮轨横向力、脱轨系数和轮重减载率。由图可知，在直线上运行时内外侧轮轨垂向力在125 kN左右，进入曲线后由于曲线超高为欠超高，曲线外侧轮对轮轨垂向力增载，反之内侧轮对轮轨垂向力减载；圆曲线上轮轨垂向力最大为156.1 kN，轮轨横向力最大为76.7 kN，脱轨系数最大为0.51，轮重减载率最大为0.25。从时域图可以看出，曲线上安装轨距杆对于轮轨相互作用力影响不大。图4（f）展示了有无轨距杆下内外侧车轮的轮轨磨耗数。由图可知，曲線上的内外侧车轮的轮轨磨耗数远大于直线上，且曲线外侧车轮轮轨磨耗数大于内侧车轮轮轨磨耗数。对比圆曲线上同侧车轮的轮轨磨耗数，其中曲线外侧车轮相差不大，安装了轨距杆时的内侧车轮处轮轨磨耗数均值较未安装轨距杆时减小了约1.6‰。

图5对比了机车以70 km/h速度分别通过有无安装轨距杆的R300 m曲线时线路轨枕横向位移、钢轨跨中轨距动态扩大量和内外侧钢轨翻转角。由图5（a）可知，安装了轨距杆的曲线段处轨枕横向位移略微增大；有无安装轨距杆时曲线段处轨枕最大横移量分别为-0.208 mm和-0.197 mm。从图5（b）可以看出，曲线线路安装轨距杆可以有效增强钢轨保持轨距的能力，圆曲线上有无安装轨距杆时的钢轨跨中轨距动态扩大量最大值分别为1.051 mm和-1.923 mm。图5（c）和5（d）展示了内外侧钢轨翻转角的动态响应，圆曲线上有无安装轨距杆时曲线外侧的钢轨最大翻转角分别为-0.382°和-0.471°，曲线内侧的钢轨最大翻转角分别为0.238°和0.163°。

从表2中可以看出，轨距杆对于轨道尤其是钢轨的动态响应影响很大。轨距杆在减小轨距动态扩大量、增强曲线线路轨距保持能力、提高线路横向稳定性的同时，可以有效的减小外侧钢轨翻转角和最大钢轨翻转角，但也会增大曲线内侧钢轨的翻转角。轨距杆还会小幅减弱曲线外侧的轮轨动态相互作用力，但相应也会增大内轨的轮轨动态相互作用力。

2.2 曲线半径和运行速度的影响

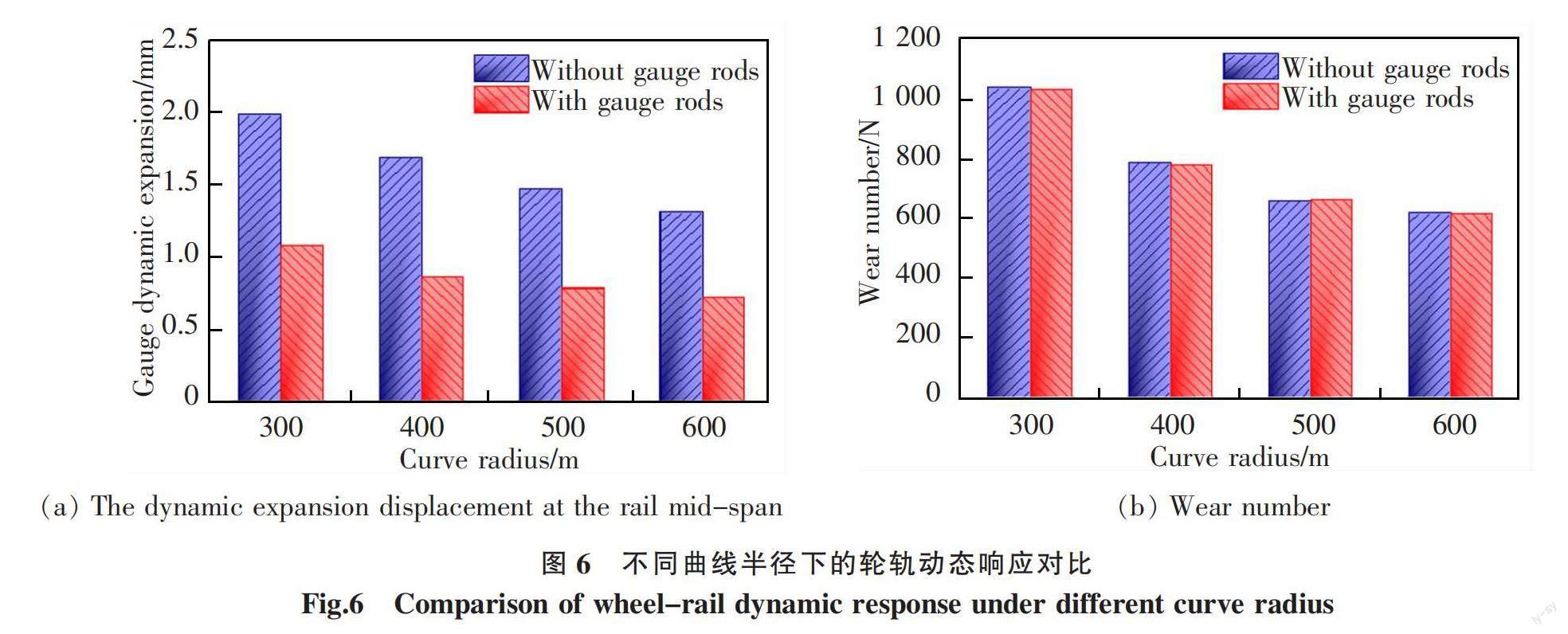
图6对比了机车以70 km/h的速度分别通过不同半径曲线时一位轮对车轮在圆曲线上时的轮轨磨耗数和钢轨跨中的最大轨距动态扩大量。由图可知，轮轨磨耗数和轨距动态扩大量随着曲线半径增大而减小；相比未安装轨距杆的曲线轨道，安装了轨距杆的轨道其轨距动态扩大量在R400 m曲线处最大减小了约48.4%；轨距杆对不同半径下的轮轨磨耗数影响不大。

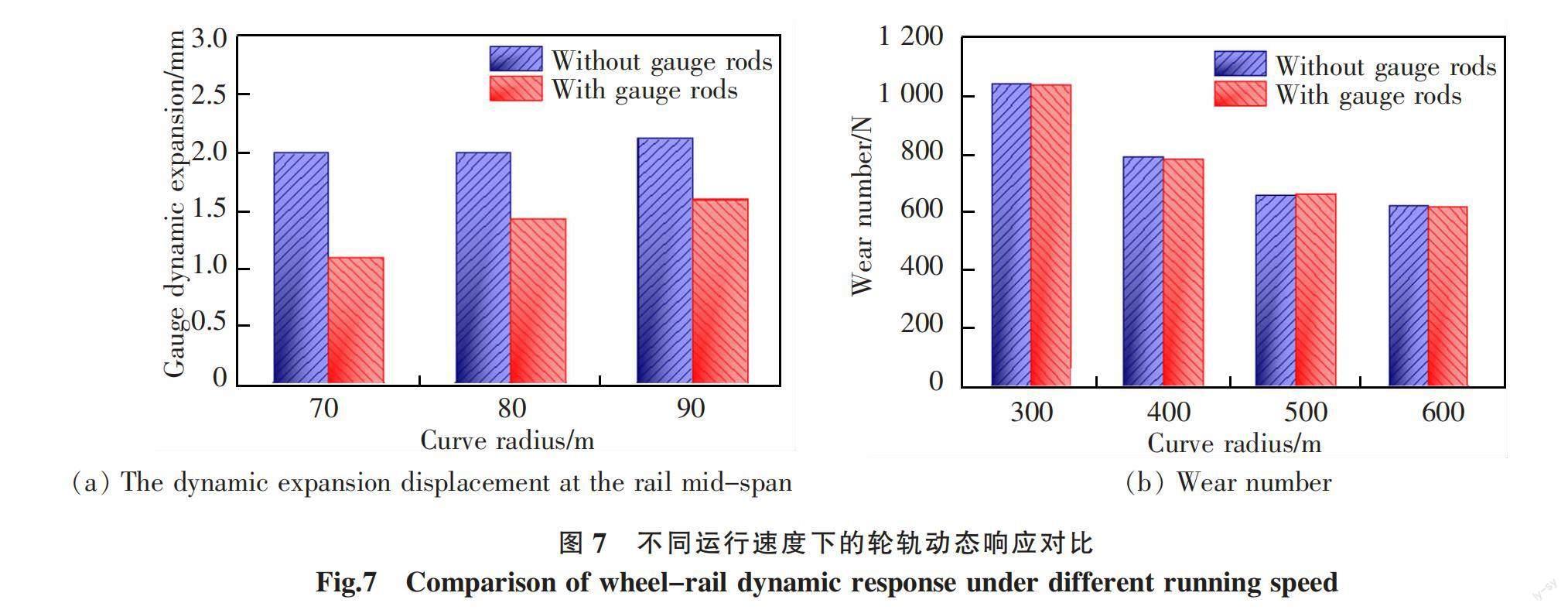
图7对比了机车以不同运行速度分别通过R300 m半径曲线时一位轮对车轮处钢轨的轨距动态扩大量和轮轨磨耗数。可以看出，轮轨磨耗数和轨距动态扩大量随着机车运行速度增大而增大；相比未安装轨距杆的曲线轨道，安装了轨距杆的轨道其轨距动态扩大量在速度为70 km/h时最大减小了约45.5%，机车在安装了轨距杆的轨道上以90 km/h的通过曲线时其最大轮轨磨耗数减小了1.42%。

2.3 轨距杆布置参数影响

《普速铁路线路维修规则》（TG/GW 102—2019）中规定半径小于450 m的曲线上每25 m钢轨需要安装10根轨距杆，对于轨枕间距为0.6 m的线路曲线时应当每4个轨跨布置一根轨距杆。为分析轨距杆布置间隔对轨道横向稳定性的影响，仿真分析了机车以70 km/h速度通过轨距杆布置间距为1～10个轨跨长度R400 m曲线时的线路动态响应。

由图8可知，曲线上的最大轨距动态扩大量随着轨距杆布置密度减小而增大，轨距杆布置间距超过4个轨跨时的轨距动态扩大量与未安装轨距杆时的动态扩大量相差不大。当轨距杆布置间距由4个轨跨减小至3个轨跨时，轨距动态扩大量将降低36.3%；轨距杆布置间距减小至2个轨跨时，轨距动态扩大量将降低77.9%。

3 结论

本文基于车辆-轨道耦合动力学理论，分析了轨距杆对重载铁路小半径曲线轮轨动力学性能和轮轨磨耗的影响，得出以下结论。

1） 轨距杆可以减小曲线上轨道的轨距动态扩大量和钢轨最大翻转角，相比未安装轨距杆的曲线，安装了轨距杆的曲线其内侧钢轨的接触点更靠近曲线内侧。

2） 机车通过有无轨距杆的小半径曲线时的轮轨磨耗数和轨距动态扩大量随着曲线半径减小和机车运行速度增大而增大，不同运行速度和曲线半径下轨距杆均可有效降低轨距动态扩大量。

3） 增大轨距杆布置密度可有效减小线路轨距动态扩大量。当轨距杆布置间距由4个轨跨减小至3个轨跨时，轨距动态扩大量将降低36.3%；轨距杆布置间距减小至2个轨跨时，轨距动态扩大量将降低77.9%。

参考文献：

[1] 陈鹏，刘秀波，张志川，等. 重载铁路曲线地段的轮轨接触分析[J]. 铁道建筑，2020，60（11）：123-127.

CHEN P，LIU X B，ZHANG Z C，et al. Analysis on wheel rail contact in curve section of heavy haul railway[J]. Railway Engineering，2020，60（11）：123-127.

[2] 陈雷，王新锐. 货车低速通过小半径曲线动力学性能试验分析[J]. 中国铁道科学，2009，30（6）：84-90.

CHEN L，WANG X R. Analysis on the dynamics performance of the freight car negotiating the small radius curve at low speed[J]. China Railway Science，2009，30（6）：84-90.

[3] 李敏，罗贇，杨勇军. A1A-A1A轴式动车动态通过小半径曲线动力学性能仿真与实测比较分析[J]. 机车电传动，2014（2）：35-37.

LI M，LUO Y，YANG Y J. Comparison and analysis of simulation and measured results on A1A-A1A motor vehicle dynamical negotiating small radius curve dynamic performance[J]. Electric Drive for Locomotive，2014（2）：35-37.

[4] 王坤全. 徑向转向架提速货运机车的动力学性能、牵引性能和曲线通过性能[J]. 铁道机车车辆，2004（S1）：26-30.

WANG K Q. Performance of dynamics traction and curving on raising speed freight locomotive with radial bogie[J]. Railway Locomotive &Car，2004（S1）：26-30.

[5] 王娜娜，罗世辉，马卫华. 轮径差对车辆动态曲线通过的影响[J]. 铁道机车车辆，2010，30（2）：47-49.

WANG N N，LUO S H，MA W H. Influence of wheel-diameter difference on dynamic curving performance of vehicle system[J]. Railway Locomotive &Car，2010，30（2）：47-49.

[6] 史智勇，王开云，吕凯凯，等. HSM型钢轨铣磨车动力学性能仿真分析[J]. 西南科技大学学报，2015，30（4）：29-32.

SHI Z Y，WANG K Y，LYU K K，et al. Simulation study on dynamics performances of HSM rail milling train[J]. Journal of Southwest University of Science and Technology，2015，30（4）：29-32.

[7] 刘文龙，徐延海，杨吉忠，等. 悬挂式单轨车辆曲线通过性仿真研究[J]. 广西大学学报（自然科学版），2016，41（5）：1402-1412.

LIU W L，XU Y H，YANG J Z，et al. Simulation research on curve-passing performance of the suspended monorail vehicle[J]. Journal of Guangxi University（Natural Science Edition），2016，41（5）：1402-1412.

[8] 沈钢，王捷. 轮轨型面对车辆曲线通过性及磨耗影响[J]. 同济大学学报（自然科学版），2014，42（1）：91-96.

SHEN G，WANG J. Wheel/rail profiles effects on vehicle curving behaviors and wear[J]. Journal of Tongji University（Natural Science），2014，42（1）：91-96.

[9] LIU P F，ZHAI W M，WANG K Y. Establishment and verification of three-dimensional dynamic model for heavy-haul train-track coupled system[J]. Vehicle System Dynamics，2016，54（11）：1511-1537.

[10] 刘锦辉，师多佳，刘文武. 地铁曲线地段钢弹簧浮置板轨道横向位移特性研究[J]. 华东交通大学学报，2021，38（6）：106-113.

LIU J H，SHI D J，LIU W W. Analysis on transverse displacement of steel spring floating plate track at curved section[J]. Journal of East Jiaotong University，2021，38（6）：106-113.

[11] 折成林. 重载铁路轨底坡设置对轮轨接触及轨面受力的影响[J]. 铁道勘察，2022，48（5）：104-109.

SHE C L. Influence of rail cant on wheel-rail contact and rail surface force in small radius curve section of heavy-haul railway[J]. Railway Investigation and Surveying，2022，48（5）：104-109.

[12] 许自强，董孝卿，彭中彦，等. 基于轮轨匹配的小曲线轮缘异常磨耗机理与控制措施[J]. 振动与冲击，2022，41（18）：127-133.

XU Z Q，DONG X Q，PENG Z Y，et al. Abnormal flange wear mechanism and control measures for small curve rails considering the wheel/rail matching[J]. Journal of Vibration and Shock，2022，41（18）：127-133.

[13] 丁軍君，孙树磊，李芾，等. 重载货车车轮磨耗仿真[J]. 交通运输工程学报，2011，11（4）：56-60.

DING J J，SUN S L，LI F，et al. Simulation of wheel wear for heavy haul freight car[J]. Journal of Traffic and Transportation Engineering，2011，11（4）：56-60.

[14] 李星，吴少培，王相平，等. 小半径曲线钢轨侧磨减缓措施及其对滚动接触疲劳影响研究[J]. 铁道科学与工程学报，2022，19（5）：1155-1167.

LI X，WU S P，WANG X P，et al. Side wear and rolling contact fatigue of rails on small radius curves[J]. Journal of Railway Science and Engineering，2022，19（5）：1155-1167.

[15] 马帅，刘秀波，任松斌，等. 朔黄重载铁路曲线钢轨侧磨预测研究[J]. 机械工程学报，2021，57（18）：118-125.

MA S，LIU X B，REN S B，et al. Research on side wear prediction of curve rail in Shuohuang heavy haul railway[J]. Journal of Mechanical Engineering，2021，57（18）：118-125.

[16] 毛帅，韩清强. 普通线路小半径曲线不均匀侧磨减缓措施[J]. 铁道建筑，2014（8）：113-115.

MAO S，HAN Q Q. Strengthening measures of uneven side wear of rail head at curve section with small-radius[J]. Railway Engineering，2014（8）：113-115.

[17] 翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京：科学出版社，2015.

ZHAI W M. Vehicle-track coupled dynamics[M]. 4th ed. Beijing： Science Press，2015.

[18] XIAO X B，JIN X S，WEN Z F. Effect of disabled fastening systems and ballast on vehicle derailment[J]. ASME Journal of Acoustic and Vibration，2007，129（2）：217-229.

第一作者：陈清华（1998—），男，博士研究生，研究方向为轨道车辆系统动力学。E-mail：chenqh@my.swjtu.edu.cn。

通信作者：王开云（1974—），男，研究员，博士，博士生导师，研究方向为轨道交通大系统动力学。E-mail：kywang@swjtu.edu.cn。

（责任编辑：吴海燕）